Problem solving and the art of the convincing argument
3.1 Introduction
Mathematics is used by engineers to solve problems. This usually involves developing a mathematical model. Just as when building a working model aeroplane we would hope to include all the important features, the same thing applies when building a mathematical model. We would also like to indicate the things we have had to leave out because they were too fiddly to deal with, and also those details that we think are irrelevant to the model. In the case of a mathematical model the things that have been left out are listed under assumptions of the model. To build a mathematical model, we usually need to use scientific rules about the way things in the world behave (e.g. Newton's laws of motion, conservation of momentum and energy, Ohm's law, Kirchoff's laws for circuits, etc.) and use numbers, variables, equations, and inequalities to express the problem in a mathematical language.
Some problems are very easy to describe mathematically. For instance: ‘Three people sitting in a room were joined by two others, how many people are there in the room in total?’ This can be described by the sum 3 + 2 =? and can be solved easily as 3 + 2 = 5.
The final stage of solving the problem is to translate it back into the original setting – the answer is: ‘there are 5 people in the room in total'.
Assumptions were used to solve this problem. We assumed that no one else came in or left the room in the meantime and we made general assumptions about the stability of the room, for example, the building containing it did not fall down. However, these assumptions are so obvious that they do not need to be listed. In more complex problems it is necessary to list important assumptions as they may have relevance as to the validity of the solution.
Another example is as follows: ‘There are three resistors in series in a circuit, two of the resistors are known to have resistance of 3 and 4 ohm, respectively. The voltage source is a battery of 12 V and the current is measured as 1 A. What is the resistance of the third resistor?’
To help express the problem in a mathematical form we may draw a circuit diagram as in Figure 3.1.

The problem can be expressed mathematically by using Ohm's law and the fact that an equivalent resistance to resistances in series is given by the sum of the individual resistances. If x is the unknown value of the third resistance and V = RI where R = R1 + R2 + R3, we obtain:
![]()
The expression of the mathematical problem has taken the form of an equation where we now need to find x, the value of the third resistance.
The main assumptions that have been used to build this mathematical model are:
(1) There are such things as pure resistors that have no capacitance or inductance.
(2) Resistances remain constant and are not affected by any possible temperature changes or other environmental effects.
(3) The battery gives a constant voltage that does not deteriorate with time.
(4) The battery introduces no resistance to the circuit.
These assumptions are simplifications that are acceptable because although the real world cannot behave with the simplicity of the mathematical model, the amount of error introduced by making these assumptions is small.
Once we have the solution of a mathematical model then it should be tested against a real-life situation to see whether the model behaves reasonably closely to reality. Once the model has been accepted then it can be used to predict the behaviour of the system for input values other than those that it has been tested for.
The stages in solving a problem are as follows:
(1) Take to real problem and express it as a mathematical one using any necessary scientific rules and assumptions about the behaviour of the system and using letters to represent any unknown quantities. Include an account of any important assumptions and simplifications made.
(2) Solve the mathematical problem using your knowledge of mathematics.
(3) Translate the mathematical solution back into the setting of your original problem.
(4) Test the model solutions for some values to check that it behaves like the real-life problem.
Most mathematical problems are expressed by using equations, or inequalities, differential or difference equations, or by expressing a problem geometrically or a combination of all of these. We might need to incorporate a random element which results in the need to use a probabilistic model. In many of the following chapters we will look at the modelling process in more detail as we come across new mathematical tools and the situations in which they are used. To perform the entire modelling cycle properly, we need to be able to test our results in a real-life situation in order to reconsider assumptions used in the model. This would require access to engineering situations and tools. For this reason, engineering mathematics books tend to concentrate on those models that are commonly used by engineers. Many of the applied problems presented in the following chapters however do present an opportunity to move from an English language description of a problem to a mathematical language description of a problem, which is an important step in the modelling process.
In this chapter, we will look at translating a problem into mathematical language and, for the main part of the chapter, we concentrate on solving a mathematical problem and the reasoning that is involved in so doing. To solve the problem using your knowledge of mathematics, we need to use the ideas of mathematical statements and how to decide whether, and express the fact that, one statement leads logically on to the next. We shall mainly use examples of solving equations and inequalities although the same ideas apply to the solving of all problems.
3.2 Describing a problem in mathematical language
The stages in expressing a problem in mathematical language can be summarized as:
(1) Assign letters to represent the unknown quantities.
(2) Write down the known facts using equations and inequalities, and using drawings and diagrams where necessary.
(3) Express the problem to be solved mathematically.
This is not a simple process because it involves a great deal of interpretation of the original problem. It is useful to try to limit the number of unknowns used as much as possible, or the problem may appear more difficult than necessary.
Example 3.1
Express the following problem mathematically: A web development company employs a freelance web designer and a freelance graphic designer to put up listings for new businesses on to their virtual business park website. Business customers are charged €200 per year for a listing. The fixed costs of the web development company amount to €2000 per week over 52 weeks in the year. The web designer charges €80 per listing and the graphic designer €100 per listing and both can prepare these at the rate of 2.4 listings in a day. The freelancers work for up to 200 days per year. How many listings does the company need in the first year to break even?
Solution The mathematical problem can be expressed by firstly assigning letters to some of the unknown quantities and then write down all the known facts as equations or inequalities.
First assign letters: Total number of listings of businesses on the park in the first year is L. LW is the number of listings prepared by the web designer and LG is the number of listings prepared by the graphic designer. The costs are K per year and the profit is P. The known facts can be expressed as follows:
![]()
This expresses the fact that the total number of listings L is made up of those prepared by the web designer and those prepared by the graphic designer. As there are up to 200 working days in a year and they both do a maximum of 2.4 listings per day.
![]()
The costs, K, are; fixed costs of 2000 × 52, plus the cost of the freelance web designer at 80LW, plus the cost of the freelance graphic designer at 100LG. This can be expressed as:
![]()
We need to relate the profit to the other variables. As the profit is 200 multiplied by the number of jobs minus the total costs, we get:
![]()
Finally, we must express the mathematical problem that we would like to solve. For the web development business to make a profit in the first year then the profit must be positive, hence we get the problem expressed as: Find the minimum L such that P > 0.
Example 3.2
Express the following in mathematical language: A car brake pedal, as represented in Figure 3.2(a) is pivoted at point A. What is the force on the brake cable if a constant force of 900 N is applied by the driver's foot and the pedal is stationary.
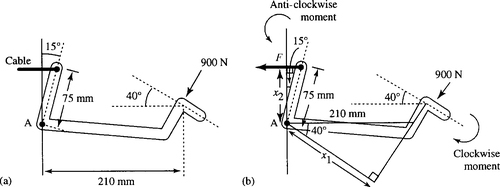
Solution First, we assign letters to the unknowns. Let F = the force on the brake cable.
In order to write down the known facts we need to consider what scientific laws can be used. As the force applied on the pedal initially provides a turning motion then we know to use the ideas of moments. The moment of a force about an axis is the product of the force F and its perpendicular distance, x, to the line of action of the force. Furthermore, as the pedal is now stationary, then the moments must be balanced so the clockwise moment must equal the anti-clockwise moment.
To use this fact, we need to use two further measurements, currently unknown, the perpendicular distance from the line of action of the force provided by the driver to the axis, A. This is marked as x1 m on the diagram in Figure 3.2(b). The other distance is the perpendicular distance from the line of action of the force on the cable to the axis A. This is marked as x2 m in Figure 3.2(b).
We can now write down the known facts, involving the unknowns x1, x2, and F. From the right angle triangle containing x1, we have (converting 210 mm = 0.21 m),
![]()
From the right angle triangle containing x2, we have (converting 75 mm = 0.075 m),
![]()
The moments of the forces can now be calculated and equated. The clockwise moment is 800xl and the anti-clockwise moment is given by Fx2 and hence we have:
![]()
Finally, we need to express the problem we are trying to solve. In this case it is simply ‘what is F?’.
Note that in both Examples 3.1 and 3.2, certain modelling assumptions had been used in order to formulating the ‘natural language’ description of the problem that we were given. For instance, it is probable that the business park listings for the business park in Example 3.1 are not all identical and therefore average figures for times and costings have been used. Similarly, in Example 3.2 no mention has been made of friction would provide an extra force to consider. Here we have only considered the transition from natural language and accompanying diagrams to the mathematical problem. We have implicitly assumed that the modelling process can be performed in two stages. From real-life problem to a natural language description which incorporates some simplifying assumptions, and then from there to a mathematical description. In reality modelling a system is much more involved. We would probably repeat stages in this process if we decided that the mathematical description was too complex and return to the real-life situation in order to make new assumptions.
We are now in a position to discuss mathematical statements and how to move from the statement of the problem to finding the desired solution.
3.3 Propositions and predicates
When we first set up a problem to be solved, we write down mathematical expressions like:
and
These are mathematical statements with an unknown value. Statements containing unknowns (or variables) are called predicates. A predicate can be either true or false depending on the value(s) substituted into it. When values are substituted into a predicate it becomes a simple proposition. If in Equation (3.1) we substitute 5 for the question mark we get:
![]()
If, however, we substitute 6 we get:
![]()
2 + 3 = 5 and 2 + 3 = 6 are examples of propositions. These are simple statements that can be assigned as either true or false. They contain no unknown quantities. Notice that if we simply rewrite a proposition or predicate we use ‘≡’ or ‘⇔’ to mean ‘is equivalent to’ or ‘is the same as’.
In Equation (3.2) if we substitute 4 for x we get:
12 = 11 which is false
but, if we substitute 5 for x we get
12 = 12 which is true.
Example 3.3
Assign true or false to the following:
(a) (3x –2)(x + 5) = 10 where x = 1
(b) 5x2 − 2x + 1 = 25 where x = −2
(c) y > 5t + 3 where y = 2 and t = −3
Solution
(a) Substitute x = 1 in the expression and we get:

(b) Substituting x = −2 into 5x2− 2x + 1 = 25 gives

(c) Substituting y = 2 and t = −3 into y > 5t + 3 gives

Like functions, predicates have a domain which is the set of all allowed inputs to the predicate. For instance, the predicate 1/ (x – 1) = 1, where x ∈ ![]() , has the restriction that x ≠ 1, as letting x equal 1 would lead to an attempt to divide by 0, which is not defined.
, has the restriction that x ≠ 1, as letting x equal 1 would lead to an attempt to divide by 0, which is not defined.
![]() where x ∈
where x ∈ ![]() has the restriction that x ≥ 2, as values of x less than 2 would lead to an attempt to take the square root of a negative number, which is not defined.
has the restriction that x ≥ 2, as values of x less than 2 would lead to an attempt to take the square root of a negative number, which is not defined.
3.4 Operations on propositions and predicates
Consider the problem given in Example 3.1. Notice that the conditions that we discovered when writing down the known facts must all be true in any solution that we come up with. If any one of these conditions is not true then we cannot accept the solution. The first condition must be true and the second and the third, etc.
Here we have an example of an operation on predicates. In Chapter 1, we defined an operation on numbers is a way of combining two numbers to give a single number. ‘And’, written as ∧ is an operation on two predicates or propositions which results a single predicate or proposition.
Therefore, to express the fact that both L ≥ 0 and L = LW + LG we can write
![]()
and the compound statement is true if each part is also true.
As propositions can only be either true (T) or false (F), all possible
outcomes of the operation can easily be listed in a small table called a truth table. The truth table for the operation of ‘and’ is given in Table 3.1. p and q represent any two propositions, for instance, for some given values of L, LW, and LG, p and q could be defined by:
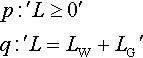
Table 3.1
Truth table for the operation ‘and’. This table can also be expressed by T Λ T ⇔ T, TΛF ⇔F, FΛ T ⇔F, F Λ F ⇔ F. T stands for ‘true’ and F stands for ‘false’
| P | q | p ∧ q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Another important operation is that of ‘or’. One example of the use of this operation comes about by solving a quadratic equation. One way of solving quadratic equations is to factorize an expression which is equal to 0.
To solve x2 –x− 6 = 0, the left-hand side of the equation can be factorized to give (x − 3) (x + 2) = 0.
Now we use the fact that for two numbers multiplied together to equal 0 then one of them, at least, must be 0, to give:
![]()
‘or’ can be written using the symbol ∨. The compound statement is true if either x − 3 = 0 is true or if x + 2 = 0 is true. Therefore, to express the statement that either x − 3 = 0 or x + 2 = 0 we can write:
![]()
∨ is also called ‘non-exclusive or’ because it is also true if both parts of the compound statement are true. This usage is unlike the frequent use of ‘or’ in the English language, where it is often used to mean a choice, for example, ‘you may have either an apple or a banana’ implies either one or the other but not both. This everyday usage of the word ‘or’ is called ‘exclusive or’.
The truth table for ‘or’ is given in Table 3.2.
Table 3.2
Truth table for ‘or’, This table can also be expressed by T∨T ⇔ T, T∨F ⇔ T,F∨T ⇔ T, F∨F ⇔ F
| P | q | p ∨ q |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
A further operation is that of ‘not’ which is represented by the symbol ¬. For instance, we could express the sentence ‘x is not bigger than 4’ as¬(x > 4).
The truth table for ‘not’ is given in Table 3.3.
Example 3.4
Assign truth values to the following:
(b) ![]()
(c) ![]()
(d) ![]()
Solution
(a) x − 2 = 3 ∧ x2= 4 when x = 2
Substitute x = 2 into the predicate, x − 2 = 3 ∧ x2 = 4 and we get 2 − 3 = 3 ∧ 22 = 4.
The first part of the compound statement is false and the second part is true. Overall, as F ∧ T ⇔ F, the proposition is false.
(b) x – 2 = 3 ∨ x2 = 4 when x = 2
Substitute x = 2 into the predicate and we get
2 − 2 = 3 ∨ 22 = 4
The first part of the compound statement is false and second part is true. As F ∨ T ⇔ T, the proposition is true.
(c) ¬(x − 4 = 0) when x = 4
When x = 4 the expression becomes:
![]()
(d)

Overall, T ∨ F ⇔ T so ¬ ((a –b) = 4) ∨ (a + b) = 2 when a = 5, b = 3 is true.
Example 3.5
Represent the following inequalities on a number line:
(b) x < 2 ∨ x ≥ 4
(c) ¬ (x < 2)
Solution
(a) x > 2 ∧ x ≤ 4. To represent the operation of ‘and’, find where the two regions overlap (Figure 3.3a). x > 2 ∧ x ≤ 4 can also be represented by 2 < x ≤ 4.

(b) x < 2 ∨ x ≥ 4. To represent the operation of ∨, ‘or’, take all points on the first highlighted region as well as all points in the second highlighted region and any end points (Figure 3.3b).
(c) ¬(x < 2). To represent the operation of ‘not’ take all the points on the number line not in the original region (Figure 3.3c). This can also be expressed by x ≥ 2.
3.5 Equivalence
We can now express an initial problem in terms of a predicate, probably an equation, a number of equations, or a number of inequalities. However, to solve the problem we need to be able to move from the original expression of the problem toward the solution. In Chapter 3 of the Background Mathematics Notes, available on the companion website for this book, we discussed how to solve various types of equations and introduced the idea of equivalent equations. In Chapter 2 we also looked at equivalent inequalities. In both cases we used the idea that in moving from one expression to an equivalent expression the set of solutions remained the same. In general, two predicates are equivalent if they are true for exactly the same set of values. We use our knowledge of mathematics to determine what operations can be performed that will maintain that equivalence. The rule that can be used to move from one equation to another was given as: ‘Equations remain equivalent if the same operation is performed to both sides of the equation’. In the case of quadratic equations we can also use a formula for the solution or use a factorization and the fact that:
![]()
In passing from one equation to an equivalent equation we should use the equivalence symbol. This then makes a mathematical sentence:

can be read as ‘The equation x + 5 = 3 is equivalent to x = 3–5’.
In all but the most obvious cases, it is a good practice to list a short justification for the equivalence by the side of the expression.

Because of the possibility of making a mistake, the solution(s) should be checked by substituting the values into the original expression of the problem. To check, substitute x = − 2 into the original equation giving − 2 + 5 = 3 which is true, indicating that the solution is correct.
Example 3.6
Solve the following equation:
![]()
Solution
![]()

Check by substituting x = 8/3 into the original equation:

We looked at methods of solving inequalities in Chapter 2. The rules for finding equivalent inequalities were: ‘Perform the same operation to both sides’; but in the case of a negative number when multiplying or dividing the direction of the inequality sign must be reversed. To solve more complex inequalities, such as f (x) > 0, f (x) < 0, where f (x) is a continuous but non-linear function, then we solve f (x) = 0 and then use a number line to mark regions where f (x) is positive, negative or zero. The important thing in the process is to present a short justification of the equivalence. Finally, when the set of solutions has been found, some of the solutions can be substituted into the original expression of the problem in order to check that no mistakes have been made.
Example 3.7
Solve the following inequalities:
(b) ![]()
Solution
Check: Test a few values from the set x > −1 and substitute into 3x − 1 < 6x + 2
Try x = 0: this gives −1 < 2 ⇔ T
Try x = 2: this gives 3(2) − 1 < 6(2) + 2 ⇔ 5 < 14 ⇔ T
Write the inequality with 0 on one side of the inequality sign
![]()
Find the solutions to f (x) = 0 where f (x) = x2 − 5x + 6 and mark them on a number line as in Figure 3.4.

![]()
(using the formula for solution of quadratic equations)

Using the fact that the function is continuous, we can substitute values for x which lie on either side of the roots of f(x) = 0 in order to find the sign of the function in that region. Here, we choose 0, 2.5, and 4 and find that

These regions are marked on the number line as in Figure 3.4 and this gives the solution to f(x) > 0 as x < 2 ∨ x > 3.
Check: A check is to substitute some values from the solution set x < 2 ∨x > 3 into the original predicate x2 − 5x > −6
Substitute x = 1, this gives 1–5 > −6 ⇔ −4 > −6 ⇔ T
Substitute x = 5, this gives 25–25 > −6 ⇔ 0 < −6 ⇔ T
It therefore appears that this solution is correct.
3.6 Implication
We previously described one method of finding equivalent equations as that of ‘doing the same thing to both sides’. This was rather simplistic but a useful way of seeing it at the time. There are only certain things that can be ‘done to both sides’ like adding, subtracting, multiplying by a non-zero expression, or dividing by a non-zero expression that always maintain equivalence. There are also many operations that can be performed to both sides of an equation which do not give an equivalent equation but give an equation with the same solutions and yet more besides. In this situation we say that the first equation implies the second equation. The symbol for implies is ⇒.
An example of implication is given by squaring both sides of the equation
![]()
The first predicate x − 2 = 2 has only one solution, x = 4, the second predicate has two solutions x = 4 and x = 0. By squaring the equation we have found a new equation which includes all the solutions of the first equation, and has one more beside. Implication is expressed in English by using phrases like ‘If … then …’.
An expression involving an implication cannot always be turned the other way around in the same way as those involving equivalence can. An example of this is given by the following statement. It is true that: ‘If I am going to work then I take the car’ which can be written using the implication symbol as:
‘I am going to work’ ⇒ ‘I take the car’
However, it is not true that:
‘If I take the car then I am going to work’
This is because there are more occasions when I take the car than simply going to work.
More examples are:
‘I only clean the windows if it is sunny’
‘I am cleaning the windows’ ⇒ ‘it is sunny’
This does not mean that ‘If it is sunny then I clean the windows’, as there are some sunny days when I have to go to work or just laze in the garden, or I am on holiday.
An implication sign can be written, and read, from left to right
‘It is sunny’⇐‘I am cleaning the windows’
which I can still read as ‘I am cleaning the windows therefore it is sunny’ or I could try rearranging the sentence as ‘Only if it is sunny will I clean the windows’.
The various ways of expressing these sentiments can get quite involved. The important point to remember is that p⇒q means that q must be true for all the occasions that p is true, but q could be true on more occasions besides. Going back to equations or inequalities:
![]()
means that the solution set, P, of p is a subset of the solution set, Q, of q. This is pictured in Figure 3.5.
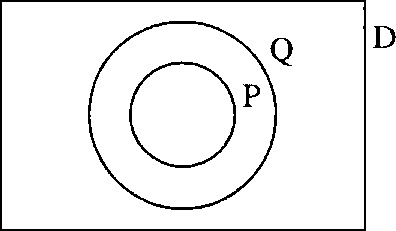
We can now see that for two equations or inequalities to be equivalent then p ⇒ q and q ⇒ p. This means that their solution sets are exactly the same (Figure 3.6).

Example 3.8
Fill in the correct symbol in each case either⇒, ⇐or⇔
(b) 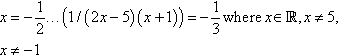
(c) (x − 3)(x − 1) > 0… x > 3 ∨ x < 1
Solution
(a) x2 − 9 = 0 ··· x = −3
Solving x2 − 9 = 0 gives
![]()
Hence, − 3 is only one of the solutions of the first equation so the correct expression is
![]()
![]()

(multiplying both sides by (2x–5)(x + 1) and as x ≠ 5, x ≠ 1)

(adding 3 on to both sides of the equation)

(using the quadratic formula to solve the equation)


has more solutions than the first predicate ![]() . Thus, the correct
. Thus, the correct

(c) (x − 3)(x – 1) > 0 ··· x > 3 ∨ x < 1
Solve the inequality on the left by firstly solving f(x) = 0:
![]()
Choosing values on either side of the roots, for example 0,2,4 gives

This is then marked on a number line as in Figure 3.7.

As the solution to (x − 3) (x − 1) > 0 is x < 1 ∨ x > 3; we have therefore shown that (x − 3)(x − 1) > 0 ⇔ x > 3 ∨ x < 1.
3.7 Making sweeping statements
In Chapter 1 of the Background Mathematics Notes, available on the companion website for this book, we made some statements about numbers which we stated were true for all real numbers. Some of these were the commutative laws:
![]()
and the distributive law:
![]()
There is a symbol which stands for ‘for all’ or ‘for every’ which allows these laws to be expressed in a mathematical shorthand

Rules, such as the commutative law, are axioms for numbers and need not be proved true. However, more involved expressions, such as
![]()
need to be justified.
If the symbol ‘for all’ is used with a predicate about its free variable then it becomes a simple proposition which is either true or false. To show that an expression is true we use our knowledge of mathematics to write equivalent expressions until we come across an expression which is obviously true (like a = a). To prove it is false is much easier. As we have made a sweeping statement about the expression and said it is true for all a, b then we only need to come across one example of numbers which make the expression false.
Example 3.9
Are the following true or false? Justify your answer.
(a) ∀a, b ∈ ![]() , a3 − b3 = (a − b)(a2 + ab + b2)
, a3 − b3 = (a − b)(a2 + ab + b2)
(b) ∀t ∈ ![]() , where t ≠ 1, t ≠ −1 1/(t + 1) = (t − 1)/(t2 − 1)
, where t ≠ 1, t ≠ −1 1/(t + 1) = (t − 1)/(t2 − 1)
(c) ∀x ∈ ![]() , where x ≠ 0 (x2 − 1) /x = x − 1
, where x ≠ 0 (x2 − 1) /x = x − 1
Solution
(a) ![]()
Looking at the right-hand side of the equality we have
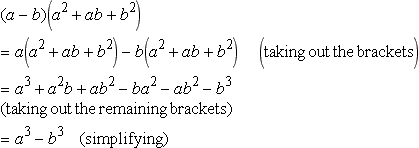
We have shown that the right-hand side is equal to the left-hand side
![]()
which is true. Therefore
![]()
is true.
(b) ![]()
Take the right-hand side of the equality

![]()
![]()
(c)

To show this is false, substitute a value for x, for example, x = 2. When x = 2
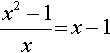
![]()
As the predicate fails for one value of x then
![]()
is false.
Another useful symbol is ∃, which means, ‘there exists’. This can be used to express the fact that every real number has an inverse under addition. Hence, we get
![]()
If the symbol ∃ is used with a predicate about its free variable, it becomes a simple proposition which is either true or false. In the case of the example given concerning the inverse, this is an axiom of the real numbers and we can just state it is true. Other statements involving existence will need some justification. Proving existence is simpler than disproving it. If I were to state ‘There exists a blue moon in the universe’ to prove this to be true I only need to find one blue moon but to disprove it I must find all the moons in the universe and show that not one of them is blue.
In other words, to show that some value exists which makes a certain predicate into a true proposition then we only need to find that value and demonstrate that the resulting proposition is true. To show that no value exists, however, is more difficult and if the domain of interest is a set of numbers we need to present an argument about any member of the set.
Example 3.10
Are the following true or false? Justify your answer.
(b) ![]()
Solution
(a) ![]()
To show this is true, we only need find one value of x which makes the equality correct. For instance, take x = −2: when x = −2, (x + 2)(x – 1)= 0 becomes (–2 + 2)(–2 − 1) = 0⇔ 0 = 0, which is true.
Therefore,∃x ∈ ![]() , (x + 2) (x – 1) = 0 is true.
, (x + 2) (x – 1) = 0 is true.
(b) ![]()
Trying a few values for x (e.g. −1, 0, 20, −2) we might suspect that this statement is false. We need to present a general argument in order to convince ourselves of this.
x2 is always positive or zero, that is, x2 ≥ 0 for all x. If we then add on 4, then for all x, x2+ 4 ≥ 4 and as 4 is bigger than 0.
x2 + 4 > 0 for all x; hence,
∃x ∈ ![]() , x2 + 4 < 0 is false.
, x2 + 4 < 0 is false.
3.8 Other applications of predicates
Predicates are often used in software engineering. Some simpler applications are:
(a) To express the condition under which a program block will be carried out (or a loop will continue execution).
(b) To express a program specification in terms of its pre- and post-conditions.
Example 3.11
Express the following in pseudo-code: print x and y if y is a multiple of x and x is an integer between 1 and 100 inclusive.
Solution Pseudo-code is a system of writing algorithms which is similar to some computer languages but not in any particular computer language. We can use any symbols we like as long as the meaning is clear.
y is a multiple of x means that if y is divided by x then the result is an integer. This can be expressed as
![]()
The condition that x must lie between 1 and 100 can be expressed as x ≥ 1 and x ≤ 100. Combining these conditions gives the following interpretation for the algorithm:

print x, y
endif
Example 3.12
A program is designed to take a given whole positive number, x, greater than 1, and find two factors of x,a and b, which multiplied together give x. a and b should be whole positive numbers different from 1, unless x is prime. Express the pre- and post-conditions for the program.
Solution Pre-condition is ![]()
The post-condition is slightly more difficult to express. Clearly ab = x is a statement of the fact that a and b must multiply together to give x. Also a and b must be elements of ![]() . a and b cannot be 1 unless x is prime, this can be expressed by
. a and b cannot be 1 unless x is prime, this can be expressed by
![]()
Finally, we have the post-condition as
![]()
3.9 Summary
(1) The stages in solving a real-life problem using mathematics are:
(a) Express the problem as a mathematical one, using any necessary scientific rules and assumptions about the behaviour of the system and using letters to represent any unknown quantities. This is called a mathematical model.
(b) Solve the mathematical problem by moving from one statement to an equivalent statement justifying each stage by using relevant mathematical knowledge.
(c) Check the mathematical solution(s) by substituting them into the original formulation of the mathematical problem.
(d) Translate the mathematical solution back into the setting of the original problem.
(e) Test the model solutions for some realistic values to see how well the model correctly predicts the behaviour of the system. If it is acceptable, then the model can be used to predict more results.
(2) A predicate is a mathematical statement containing a variable. Examples of predicates are equations and inequalities.
(3) If values are substituted into a predicate it becomes a simple proposition which is either true or false.
(4) The three main operations on predicates and propositions are ∧, ∨, ¬, and these can be defined using truth tables as in Tables 3.1–3.3.
(5) Two predicates, p, q, are equivalent (p ⇔ q) if they are true for exactly the same set of values.
(6) p ⇒ q means ‘p implies q’, that is, q is true whenever p is true. If p, q are equations or inequalities and p ⇒ q then all solutions of p are also solutions of q and q may have more solutions besides.
(7) The symbol ∀ stands for ‘for all’ or ‘for every’ and can be used with a predicate to make it into a simple proposition, for example, ![]() which is true.
which is true.
(8) The symbol ∃ stands for ‘there exists’ and can also be used with a predicate to make it into a simple proposition, for example, ![]() which is true.
which is true.
3.10 Exercises
3.1 Assign T or F to the following
(b) 2x + 2 = 10 when x = 2
(c) 3x2 + 3x − 6 = 0 when x = 1
(d) 1 − t2 = −3 when t = −2
(e) t − 5 = 6.5 ∧ t + 4 = 2.5 when t = 1.5
(f) u + 3 = 6 ∧ 2u − 1 = 4 when u = 3
(g) 3y + 2 = −2.5 ∨ 1 − y = 1 when y = −1.5
(h) ¬(x2 − x + 2 = 0) when x = −1
(i) ¬(t − 2 = 4 ∧ t = 3)
(j) ¬(t − 2 = 4) ∧ (t = 3)
(k) ¬ (3t − 4 = 6 ∨ 1 − t = −![]() ) when t =
) when t = ![]()
3.2. Solve the following, justifying each stage of the solution and checking the result.
(b) 1 − 2t2 = 1 − 10t
(c) 50t − 11 = −25t2,
(d) 30y − 13 = 8y2
(e) 10t − 4 ≤ −3,
(f) 10 − 4x > 12.
3.3. Find the range of values for which the following hold and represent them on a number line.
(b) 2−4t ≤ 3∧2−t < 1
(c) ¬(2x + 3 ≤ 9).
3.4. Fill the correct sign ⇒, ⇐ or ⇔ or indicate none of these. Assume the domain is ![]() unless indicated otherwise.
unless indicated otherwise.
(b) ![]() = 5 … x = 26 (where x ≥ 1)
= 5 … x = 26 (where x ≥ 1)
(c) t2 − 5t = 36 … (t − 4)(t − 9) = 0
(d) (2x − 2)/(x − 3) = 1 … 3x + 4 = −x (where x ≠ 3)
(e) 3x = 4 … (3x)2 = (4)2
(f) t + 1 = 5 … (t + 1)3 = 53
(g) (x + 1)(x − 3) = (x − 3)(x + 2) … (x + 1) = (x + 2)
(h) x − 1 = 25 … ![]() = 5 where x ≥ 1
= 5 where x ≥ 1
(i) ![]()
(j) ![]()
(k) ![]()
3.5. Determine whether the following statements are true or false and justify your answer.
(a) ∀a, b ∈ ![]() , a4 −b4 = (a − b)(a3 − a2 b + ab2 −b3)
, a4 −b4 = (a − b)(a3 − a2 b + ab2 −b3)
(b) ∀a, b ∈ ![]() , a3 + b3 = (a + b)3
, a3 + b3 = (a + b)3
(c) ∀x ∈ ![]() , x ≠ 0 1/(1/x) = x
, x ≠ 0 1/(1/x) = x
(d) ∃t, t ∈ ![]() , t2 − 3 = 4
, t2 − 3 = 4
(e) ∃t, t ∈ ![]() , t2 + 3 = 0.
, t2 + 3 = 0.
3.6. Write the following conditions using mathematical symbols:
(b) y is a number between 3 and 60 inclusive,
(c) w is an even number greater than 20,
(d) t differs from tn−1by less than 0.001.
3.7. Express the following problems mathematically and solve them:
(a) A set of screwdrivers cost €10 and hammers €6.50. Find the possible combinations of maximum numbers of screwdriver and hammer sets that can be bought for €40.
(b) An object is thrown vertically upwards from the ground with an initial velocity of 10 m s−l. The mass of the object is 1 kg. Find the maximum height that the object can reach using
(i) Kinetic energy (KE) is given by ![]() where m is its mass and v its velocity.
where m is its mass and v its velocity.
(ii) The potential energy (PE) is mgh, where m is the mass, g is the acceleration due to gravity (which can be taken as 10 m s−2), and h is the height.
(iii) Assuming that no energy is lost as heat due to friction, then the conservation of energy law gives KE + PE = constant.
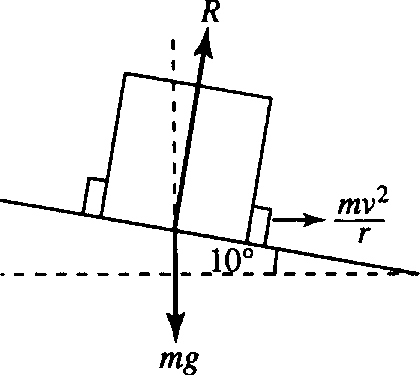
3.8. A road has a bend with radius of curvature 100 m. The road is banked at an angle of 10°. At what speed should a car take the bend in order not to experience any side thrust on the tyres? Use the following assumptions:
(a) The sideways force needed on the vehicle in order to maintain it in circular motion (called the centripetal force) = mv2/r where r is the radius of curvature of the bend, v the velocity, and m the mass of the vehicle.
(b) The only force with a component acting sideways on the vehicle, is the reactive force of the ground. This acts in a direction normal to the ground (i.e. we assume no frictional force in a sideways direction).
(c) The force due to gravity of the vehicle is mg, where m is the mass of the vehicle and g is the acceleration due to gravity (≈ 9.8 m s−2). This acts vertically downwards. The forces operating on the vehicle and ground, in a lateral or vertical direction, are pictured in Figure 3.8.