12.7 Limits and convergence

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

L'Hopital's rule

When sketching graphs of functions in Chapter 11, we looked at graphs where the function is undefined for some values of x. The function f (x) = 1/ x, for instance, is not defined when x = 0 and tends to −∞ as x → 0 and tends to $+ \infty$ $+ \infty$ as x → 0⁺. Not all functions that have undefined points tend to $\pm \infty$ $\pm \infty$ near the point where they are undefined. For example, consider the function f (x) = sin (x) / x. The graph of this function is shown in Figure 12.5. The function is not defined for x = 0, which we can see by substituting x = 0 into the function expression. This gives a zero in the denominator and hence an attempt to divide by 0 which is undefined. However, we can see from the graph that the function, rather than tending to plus or minus infinity as x → 0, just tends to 1. This is very useful because we are able to ‘patch’ the function by giving it a value at x = 0 and the new function is defined for all values of x.

f12-05-9780750658553 — Figure 12.5 The graph of the function f(x) = sin(x)/x.

We can define a new function. This particular function is quite famous, and is called the sinc function

$sinc (x) = {\begin{array}{l} \frac{sin (x)}{x} & where x \neq 0 \\ 1 & where x = 0 \end{array}$ $sinc (x) = {\begin{array}{l} \frac{sin (x)}{x} & where x \neq 0 \\ 1 & where x = 0 \end{array}$

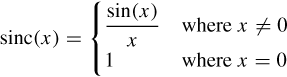
si177_e

The points where functions may tend to a finite limit can be identified by looking out for points which lead to 0/0. These are called indeterminate points, indicating that they are a special type of undefined point.

We can examine what happens to the function near the indeterminate point by using the power series expansions of the denominator and numerator. Substituting the series for sin (x)/x into the expression sin (x) gives

$\frac{sin (x)}{x} = \frac{1}{x} (x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} \dots)$ $\frac{sin (x)}{x} = \frac{1}{x} (x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} \dots)$

si178_e

and therefore

$\begin{array}{l} lim_{x \to 0} \frac{sin (x)}{x} & = lim_{x \to 0} \frac{1}{x} (x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \dots) \\ ? & = lim_{x \to 0} (1 - \frac{x^{2}}{3!} + \frac{x^{4}}{5!} - \dots) \end{array}$ $\begin{array}{l} lim_{x \to 0} \frac{sin (x)}{x} & = lim_{x \to 0} \frac{1}{x} (x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \dots) \\ ? & = lim_{x \to 0} (1 - \frac{x^{2}}{3!} + \frac{x^{4}}{5!} - \dots) \end{array}$

si179_e

The last expression is defined at x = 0, so we can substitute x = 0 in order to find the limit. This gives the value 1. L'Hopital's rule is a quick way of finding this limit without needing to write out the series specifically.

L'Hopital's rule states that if a function f(x) = g(x)/h(x) is indeterminate at x = a then:

$lim_{x \to a} \frac{g (x)}{h (x)} = lim_{x \to a} \frac{g^{'} (x)}{h^{'} (x)} .$ $lim_{x \to a} \frac{g (x)}{h (x)} = lim_{x \to a} \frac{g^{'} (x)}{h^{'} (x)} .$

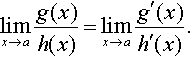
si180_e

If g′ (x) / h′ (x) is defined at x = a, we can then use

$lim_{x \to a} \frac{g^{'} (x)}{h^{'} (x)} = \frac{g^{'} (a)}{h^{'} (a)}$ $lim_{x \to a} \frac{g^{'} (x)}{h^{'} (x)} = \frac{g^{'} (a)}{h^{'} (a)}$

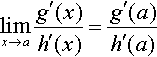
si181_e

and if g′ (x) / h′ (x) is indeterminate at x = a, we can use the rule again.

We can show this to be true by using Equation (12.13) for the Taylor series expansion about a:

$\frac{g (x)}{h (x)} = \frac{g (a) + g^{'} (a) (x - a) + (g^{″} (a) / 2!) {(x - a)}^{2} + \cdot \cdot \cdot}{h (a) + h^{'} (a) (x - a) + (h^{″} (a) / 2!) (x - a) ?^{2} + \cdot \cdot \cdot}$ $\frac{g (x)}{h (x)} = \frac{g (a) + g^{'} (a) (x - a) + (g^{″} (a) / 2!) {(x - a)}^{2} + \cdot \cdot \cdot}{h (a) + h^{'} (a) (x - a) + (h^{″} (a) / 2!) (x - a) ?^{2} + \cdot \cdot \cdot}$

si182_e

and given that g(a) = 0 and h(a) = 0

$\begin{array}{l} lim_{x \to a} \frac{g (x)}{h (x)} & = lim_{x \to a} \frac{g^{'} (a) (x - a) + (g^{″} (a) / 2!) {(x - a)}^{2} + \cdot \cdot \cdot}{h^{'} (a) (x - a) + (h^{″} (a) / 2!) {(x - a)}^{2} + \cdot \cdot \cdot} \\ ? & = lim_{x \to a} \frac{g^{'} (a) + (g^{″} (a) / 2!) (x - a) + \cdot \cdot \cdot}{h^{'} (a) + (h^{″} (a) / 2!) (x - a) + \cdot \cdot \cdot} \\ ? & = \frac{g^{'} (a)}{h^{'} (a)} ? (if h^{'} (a) \neq 0) . \end{array}$ $\begin{array}{l} lim_{x \to a} \frac{g (x)}{h (x)} & = lim_{x \to a} \frac{g^{'} (a) (x - a) + (g^{″} (a) / 2!) {(x - a)}^{2} + \cdot \cdot \cdot}{h^{'} (a) (x - a) + (h^{″} (a) / 2!) {(x - a)}^{2} + \cdot \cdot \cdot} \\ ? & = lim_{x \to a} \frac{g^{'} (a) + (g^{″} (a) / 2!) (x - a) + \cdot \cdot \cdot}{h^{'} (a) + (h^{″} (a) / 2!) (x - a) + \cdot \cdot \cdot} \\ ? & = \frac{g^{'} (a)}{h^{'} (a)} ? (if h^{'} (a) \neq 0) . \end{array}$

si183_e

Example 12.32

Find

$lim_{x \to 1} \frac{x^{3} - 2 x^{2} + 4 x - 3}{4 x^{2} - 5 x + 1} .$ $lim_{x \to 1} \frac{x^{3} - 2 x^{2} + 4 x - 3}{4 x^{2} - 5 x + 1} .$

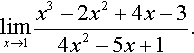
si184_e

Solution Substituting x = 1 into

$\frac{x^{3} - 2 x^{2} + 4 x - 3}{4 x^{2} - 5 x + 1}$ $\frac{x^{3} - 2 x^{2} + 4 x - 3}{4 x^{2} - 5 x + 1}$

si185_e

gives 0/0, which is indeterminate. Using L'Hopital's rule, we differentiate the top and bottom lines:

$lim_{x \to 1} \frac{x^{3} - 2 x^{2} + 4 x - 3}{4 x^{2} - 5 x + 1} = lim_{x \to 1} \frac{3 x^{2} - 4 x + 4}{8 x - 5} .$ $lim_{x \to 1} \frac{x^{3} - 2 x^{2} + 4 x - 3}{4 x^{2} - 5 x + 1} = lim_{x \to 1} \frac{3 x^{2} - 4 x + 4}{8 x - 5} .$

si186_e

We find that the new expression is defined at x = 1, so

$lim_{x \to 1} \frac{3 x^{2} - 4 x + 4}{8 x - 5} = \frac{3 - 4 + 4}{8 - 5} = \frac{3}{3} = 1$ $lim_{x \to 1} \frac{3 x^{2} - 4 x + 4}{8 x - 5} = \frac{3 - 4 + 4}{8 - 5} = \frac{3}{3} = 1$

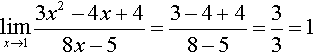
si187_e

Example 12.33

Find

$lim_{x \to 0} \frac{cos (x) - 1}{x^{2}} .$ $lim_{x \to 0} \frac{cos (x) - 1}{x^{2}} .$

si188_e

Solution Substituting x = 0 into

$\frac{cos (x) - 1}{x^{2}}$ $\frac{cos (x) - 1}{x^{2}}$

si189_e

gives 0/0, which is indeterminate. Therefore, using L'Hopital's rule, we differentiate the top and bottom lines:

$lim_{x \to 0} \frac{cos (x) - 1}{x^{2}} = lim_{x \to 0} \frac{- sin (x)}{2 x} .$ $lim_{x \to 0} \frac{cos (x) - 1}{x^{2}} = lim_{x \to 0} \frac{- sin (x)}{2 x} .$

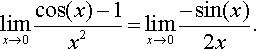
si190_e

We find that the new expression is also indeterminate at x = 0, so we use L'Hopital's rule again:

$lim_{x \to 0} \frac{- sin (x)}{2 x} = lim_{x \to 0} \frac{- cos (x)}{2} .$ $lim_{x \to 0} \frac{- sin (x)}{2 x} = lim_{x \to 0} \frac{- cos (x)}{2} .$

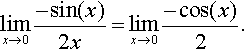
si191_e

The last expression is defined at x = 0 so we can substitute x = 0 to give

$lim_{x \to 0} \frac{- cos (x)}{2} = - \frac{1}{2} .$ $lim_{x \to 0} \frac{- cos (x)}{2} = - \frac{1}{2} .$

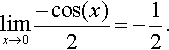
si192_e

Hence,

$lim_{x \to 0} \frac{cos (x) - 1}{x^{2}} = - \frac{1}{2} .$ $lim_{x \to 0} \frac{cos (x) - 1}{x^{2}} = - \frac{1}{2} .$

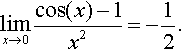
si193_e

12.7 Limits and convergence

We have already briefly mentioned ideas of limits in various contexts. We will now look at the idea in more detail. When we looked at the sum to infinity of a geometric progression in Table 12.1 we looked at S_n= 4(1 − (2/3)ⁿ) as n was made larger and discovered that S₄₀ = 4 to 7 s.f. and all values of n > 40 also gave S_n= 4 to 7 s.f. This can give us an idea of how to find out if a sequence tends to a limit:

1. Choose a number of significant figures

2. Write all terms in the sequence to that number of significant figures.

3. The sequence tends to a limit if the terms in the sequence, when expressed to the agreed number of significant figures, become constant, that is, do not change after some value of n.

Theoretically, this procedure must work for all possible numbers of significant figures. As my calculator only displays 8 s.f. I cannot go through this process for more than 7 s.f. A computer using double precision arithmetic could perform the calculations to far more (usually up to 18 s.f.).

Consider the series

$1 + z + z^{2} + z^{3} + \cdot \cdot \cdot$ $1 + z + z^{2} + z^{3} + \cdot \cdot \cdot$

which is a GP with first term 1 and common ratio z, the sum to n terms gives

$\frac{1 - z^{n}}{1 - z} .$ $\frac{1 - z^{n}}{1 - z} .$

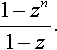
si195_e

For z = 1/2 this gives the series

$1 + \frac{1}{2} + {(\frac{1}{2})}^{2} + {(\frac{1}{2})}^{3} + \dots$ $1 + \frac{1}{2} + {(\frac{1}{2})}^{2} + {(\frac{1}{2})}^{3} + \dots$

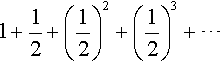
si196_e

and the sum of n terms gives

$S_{n} = \frac{1 - {(\frac{1}{2})}^{n}}{1 - \frac{1}{2}} = 2 (1 - {(\frac{1}{2})}^{n}) .$ $S_{n} = \frac{1 - {(\frac{1}{2})}^{n}}{1 - \frac{1}{2}} = 2 (1 - {(\frac{1}{2})}^{n}) .$

si197_e

We can write, S_n, as a sequence of values to 3 s.f., 5 s.f., and 7 s.f. as is done in Table 12.2.

Table 12.2

The values in the sequence S_n =expressed to 3 s.f. 5 s.f. and 7 s.f. Notice the sequence becomes constant after n = 9 for 3 s.f, after n = 15 for 5 s.f and after n = 22 for 7 s.f.

n	S_n (3 s.f.)	S_n (5 s.f.)	S_n (7 s.f.)
1	1	1	1
2	1.5	1.5	1.5
3	1.75	1.75	1.75
4	1.88	1.875	1.875
5	1.94	1.9375	1.9375
6	1.97	1.9688	1.96875
7	1.98	1.9844	1.984375
8	1.99	1.9922	1.992188
9	2	1.9961	1.996094
10	2	1.998	1.998047
11	2	1.999	1.999023
12	2	1.9995	1.999512
13	2	1.9998	1.999756
14	2	1.9999	1.999878
15	2	2	1.999939
16	2	2	1.999969
17	2	2	1.999985
18	2	2	1.999992
19	2	2	1.999996
20	2	2	1.999998
21	2	2	1.999999
22	2	2	2
23	2	2	2

cetable2

From these results we can see that the limit appears to be 2. The limit is reached to 3 s.f for n = 9, to 5 s.f for n = 15, and to 7 s.f for n = 22.

The more terms taken in a sequence which converges, then the nearer we will get to the limit. However we can only get as near as the number of significant figures, usually limited by the calculator, permits. When using a numerical method to solve a problem we use these ideas about convergence.

12.8 Newton–Raphson method for solving equations

Although we already know how to solve linear equations and quadratic equations other equations may need to be solved by using a numerical method. One such method is the Newton–Raphson method. The method consists of an algorithm which can be expressed as follows:

Step 1: take an equation and write it in the form f (x) = 0, then,

Step 2: take a guess at a solution

Step 3: calculate a new value for x using

$x \leftarrow x - \frac{f (x)}{f^{'} (x)}$ $x \leftarrow x - \frac{f (x)}{f^{'} (x)}$

si198_e

Step 4: Repeat Step 3 until come convergence criterion has been satisfied or until it is decided that the method has failed to find a solution. Here, the ‘←’ symbol has been used to represent the ‘assignment operator’.

$x \leftarrow x - \frac{f (x)}{f^{'} (x)}$ $x \leftarrow x - \frac{f (x)}{f^{'} (x)}$

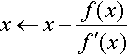
si199_e

means replace x by a value found by taking the old value of x and calculating x − f (x) / f′ (x). We will return to the problems in Steps 1 and 4 later; first we will look at a simple example of using the Newton–Raphson method.

Example 12.34

Use Newton–Raphson method to find $\sqrt{5}$ $\sqrt{5}$ correct to 7 s.f.

Solution $\sqrt{5}$ $\sqrt{5}$ is one solution to the equation x² = 5

Step 1: Write the equation in the form f(x) = 0

$\begin{array}{l} x^{2} = 5 & \Leftrightarrow & x^{2} - 5 = 0 \end{array}$ $\begin{array}{l} x^{2} = 5 & \Leftrightarrow & x^{2} - 5 = 0 \end{array}$

Step 2: Take a guess at the solution. We know that $\sqrt{5}$ $\sqrt{5}$ is slightly bigger than $\sqrt{4}$ $\sqrt{4}$ so take a first guess as x = 2.

Steps 3 and 4: Calculate

$x \leftarrow x - \frac{f (x)}{f^{'} (x)}$ $x \leftarrow x - \frac{f (x)}{f^{'} (x)}$

until some convergence criterion is satisfied.

As f(x) = x² − 5, f′(x) = 2x

$x \leftarrow x - \frac{f (x)}{f^{'} (x)}$ $x \leftarrow x - \frac{f (x)}{f^{'} (x)}$

si206_e

gives

$x \leftarrow x - \frac{x^{2} - 5}{2 x} .$ $x \leftarrow x - \frac{x^{2} - 5}{2 x} .$

si207_e

This can be written over a common denominator, giving

$x \leftarrow \frac{x^{2} + 5}{2 x}$ $x \leftarrow \frac{x^{2} + 5}{2 x}$

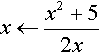
si208_e

which is the Newton–Raphson formula for solving x² − 5 = 0.

$\begin{array}{l} Start with x = 2 & x \leftarrow & \frac{4 + 5}{4} & x = 2.25 \\ Substitute x = 2.25 & x \leftarrow & \frac{{(2.25)}^{2} + 5}{2 (2.25)} & x = 2.2361111 \\ Substitute x = 2.2361111 & x \leftarrow & \frac{{(2.2361111)}^{2} + 5}{2 (2.2361111)} & x = 2.236068 \\ Substitute x = 2.236068 & x \leftarrow & \frac{{(2.236068)}^{2} + 5}{2 (2.236068)} & x = 2.236068 \end{array}$ $\begin{array}{l} Start with x = 2 & x \leftarrow & \frac{4 + 5}{4} & x = 2.25 \\ Substitute x = 2.25 & x \leftarrow & \frac{{(2.25)}^{2} + 5}{2 (2.25)} & x = 2.2361111 \\ Substitute x = 2.2361111 & x \leftarrow & \frac{{(2.2361111)}^{2} + 5}{2 (2.2361111)} & x = 2.236068 \\ Substitute x = 2.236068 & x \leftarrow & \frac{{(2.236068)}^{2} + 5}{2 (2.236068)} & x = 2.236068 \end{array}$

si209_e

We notice that in the last iteration there has been no change in the value of x, so we assume that the algorithm has converged, giving

$\sqrt{5} = 2.236068 to 7 ?s . f .$ $\sqrt{5} = 2.236068 to 7 ?s . f .$

The sequence of values we have found is:

2, 2.25, 2.2361111, 2.236068, 2.236068, and we need to stop at this point because the value of x has not changed in the last iteration.

Example 12.35

Find a solution to the equation x³ − 3x² + 2x + 1 = 0

Solution

Step 1: The equation is already expressed in the correct form.

Step 2: We need to find a first guess for the solution and to do this we could sketch the graph to see roughly where it crosses the x-axis or we could try substituting a few values into the function f (x) = x³ − 3x²+ 2x + 1 and look for a change of sign, which we have done in Table 12.3. As the function is continuous, the function must pass through zero in order to change from positive to negative, or vice versa. There is a change of sign between x = −0.5 and x = 0, so we take as a first guess a point half way between these two values, giving x = −0.25.

Table 12.3

The function f(x) = x³ − 3x² + 2x + 1 evaluated for a few values of x

x	−1	−0.5	0	0.5	1	1.5	2
f(x) = x³ − 3x² + 2x + 1	−7	−0.875	1	1.375	1	0.625	1

cetable3

Step 3: Using the Newton–Raphson formula

$x \leftarrow x - \frac{f (x)}{f^{'} (x)}$ $x \leftarrow x - \frac{f (x)}{f^{'} (x)}$

si211_e

and substituting f(x) = x³ − 3x² + 2x + 1 gives

$x \leftarrow x - \frac{x^{3} - 3 x^{2} + 2 x + 1}{3 x^{2} - 6 x + 2}$ $x \leftarrow x - \frac{x^{3} - 3 x^{2} + 2 x + 1}{3 x^{2} - 6 x + 2}$

si212_e

and simplifying gives

$x \leftarrow \frac{2 x^{3} - 3 x^{2} - 1}{3 x^{2} - 6 x + 2} .$ $x \leftarrow \frac{2 x^{3} - 3 x^{2} - 1}{3 x^{2} - 6 x + 2} .$

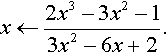
si213_e

Starting by substituting x = −0.25 gives

$x \leftarrow \frac{2 {(- 0.25)}^{3} - 3 {(- 0.25)}^{2} - 1}{3 {(- 0.25)}^{2} - 6 (- 0.25) + 2} = \frac{- 1.21875}{3.6875} = - 0.3305084$ $x \leftarrow \frac{2 {(- 0.25)}^{3} - 3 {(- 0.25)}^{2} - 1}{3 {(- 0.25)}^{2} - 6 (- 0.25) + 2} = \frac{- 1.21875}{3.6875} = - 0.3305084$

si214_e

Now substitute x = −0.3305084 giving

$x \leftarrow \frac{2 {(- 0.3305084)}^{3} - 3 {(- 0.3305084)}^{2} - 1}{3 {(- 0.3305084)}^{2} - 6 (- 0.3305084) + 2} = - 0.3247489.$ $x \leftarrow \frac{2 {(- 0.3305084)}^{3} - 3 {(- 0.3305084)}^{2} - 1}{3 {(- 0.3305084)}^{2} - 6 (- 0.3305084) + 2} = - 0.3247489.$

si215_e

Substitute x = −0.3247489 giving

$x \leftarrow \frac{2 {(- 0.3247489)}^{3} - 3 {(- 0.3247489)}^{2} - 1}{3 {(- 0.3247489)}^{2} - 6 (- 0.3247489) + 2} = - 0.3247179 .$ $x \leftarrow \frac{2 {(- 0.3247489)}^{3} - 3 {(- 0.3247489)}^{2} - 1}{3 {(- 0.3247489)}^{2} - 6 (- 0.3247489) + 2} = - 0.3247179 .$

si216_e

Substitute x = −0.3247179 giving

$x \leftarrow \frac{2 {(- 0.3247179)}^{3} - 3 {(- 0.3247179)}^{2} - 1}{3 {(- 0.3247179)}^{2} - 6 (- 0.3247179) + 2} = - 0.3247179 .$ $x \leftarrow \frac{2 {(- 0.3247179)}^{3} - 3 {(- 0.3247179)}^{2} - 1}{3 {(- 0.3247179)}^{2} - 6 (- 0.3247179) + 2} = - 0.3247179 .$

si217_e

As the last two numbers are the same to the degree of accuracy we have used, there is no point in continuing. We have thus obtained the sequence of values:

$- 0.25, ? - 0.3305084, ? - 0.3247489, ? - 0.3247179, ? - 0.3247179 .$ $- 0.25, ? - 0.3305084, ? - 0.3247489, ? - 0.3247179, ? - 0.3247179 .$

Finally, we can check that we have found a good approximation to a solution of the equation by substituting x = −0.3247179 into the function f (x) = x³ − 3x² + 2x + 1, which gives 2.441 × 10⁻⁷. As this value is very close to 0 this confirms that we have found a reasonable approximation to a solution of the equation f (x) = 0.

The convergence criterion

In Examples 12.34 and 12.35 we decided to stop the calculation when the last two values found were equal. We had found the limit of the recurrence relation to 7 s.f. In a computer algorithm, we could test if the last two calculated values of x differ by a very small amount.

Example 12.36

A convergent sequence is defined by a recurrence relation. The calculation should stop when the limit has been found to an accuracy of at least three decimal places. Give a condition that could be used in this case.

Solution Assuming two consecutive terms are x_n−1 and x_n, then the absolute difference between them is given by |x_n − x_{n − 1}|. To test whether this is small enough to accept x_n as the limit to three decimal places we use the fact that a number expressed to three decimal places could have an absolute error of just less than 0.0005. So the condition we can use to stop the algorithm could be |x_n − x_{n − 1}| < 0.0005. If this condition is satisfied we could then assume that x_n is the limit to three decimal places. To be on the safe side, however, it is better to perform the calculation one final time and check that it is also true that |x_n _{+ 1} – x_n| < 0.0005 and then use x_n+1 as the value of the limit which should be accurate to at least three decimal places.

Example 12.37

A convergent sequence is defined by a recurrence relation. The calculation should stop when the limit has been found to an accuracy of at least 4 s.f. Give a condition that could be used in this case.

Solution Assuming two consecutive terms are x_n₋₁ and x_n then the absolute difference between them is given by |x_n − x_{n − 1}|. To test whether this is small enough to accept x_n as the limit to 4 s.f. use the fact that a number expressed to 4 s.f. can have an absolute relative error of just less than 0.00005. As we do not know that value of the limit we must approximate it by the last value calculated in the sequence, so the absolute relative error is approximately

$\frac{| x_{n} - x_{n - 1} |}{| x_{n} |}$ $\frac{| x_{n} - x_{n - 1} |}{| x_{n} |}$

si219_e

so an appropriate condition would be

$\frac{| x_{n} - x_{n - 1} |}{| x_{n} |} < 0.00005$ $\frac{| x_{n} - x_{n - 1} |}{| x_{n} |} < 0.00005$

si220_e

$| x_{n} - x_{n - 1} | < 0.00005 | x_{n} | .$ $| x_{n} - x_{n - 1} | < 0.00005 | x_{n} | .$

As in the previous example it would be preferable to test that this condition holds on at least two successive iterations. Hence, we could also check that

$| x_{n + 1} - x_{n} | < 0.00005 | x_{n + 1} |$ $| x_{n + 1} - x_{n} | < 0.00005 | x_{n + 1} |$

and take x_n+1 as the limit of the sequence correct to four significant figures.

Divergence

A divergent sequence is one that does not tend to a finite limit. Some examples of divergent sequences are:

(i) 1, 0, 1, 0, 1, 0, 1, 0 … which is an oscillating sequence,

(ii) 1, 2, 4, 8, 16… which tends to plus infinity,

(iii) −1, −3, −5,… which tends to minus infinity.

Recurrence relations that are used for some numerical method may not always converge, particularly if the initial value is chosen inappropriately. To check for this eventuality, it is usual to stop the algorithm after some finite number of steps, maybe 100 or 1000 iterations, depending on the problem. If no convergence has been found after that number of iterations then it is considered that sequence is failing to converge.

12.9 Summary

1. A sequence is a collection of objects arranged in a definite order. The elements of a sequence can be represented by a₁, a₂, a₃,…, a_n,…

2. If a rule exists by which any term in the sequence can be found then this may be used to express the general term of the sequence, usually represented by a_n or a (n). This rule can also be expressed in the form of a recurrence relation where a_n+1 is expressed in terms of a_n, a_n₋₁, a_n₋₂,…

3. During analog to digital (A/D) conversion, a signal is sampled and can then be represented by a sequence of numbers. f(t) can be represented by a(n) = f(nT), where T is the sampling interval and t = nT. The sampling theorem states that the sampling interval must be less than T = 1/ (2 f) seconds in order to be able to represent a frequency of f Hz.

4. A series is the sum of a sequence. To represent series we may use sigma notation, using the capital Greek letter sigma, Σ, to indicate the summation process, for example,

$Σ_{n = 0}^{n = 10} \frac{1}{2^{n}}$ $Σ_{n = 0}^{n = 10} \frac{1}{2^{n}}$

si223_e

means ‘sum all the terms 1/2ⁿ for n from 0 to 10'.

5. An arithmetic progression (AP) is a sequence where each term is found by adding a fixed amount, called the common difference, to the previous term. If the first term is a and the common difference is d, then the general term is a_n = a + (n − 1)d and the sum of the first n terms is given by

$\begin{array}{l} S_{n} = \frac{n}{2} (2 a + (n - 1) d) & or & S_{n} = \frac{n}{2} (a + l) \end{array}$ $\begin{array}{l} S_{n} = \frac{n}{2} (2 a + (n - 1) d) & or & S_{n} = \frac{n}{2} (a + l) \end{array}$

where l is the last term in the sequence and n is the number of terms.

6. An geometric progression (GP) is a sequence where each term is found by multiplying the previous term by a fixed amount, called

the common ratio. If the first term is a and the common ratio is r, then the general term is a_n = arⁿ⁻¹, and the sum of the first n terms is given by

$S_{n} = \frac{a (1 - r^{n})}{1 - r} .$ $S_{n} = \frac{a (1 - r^{n})}{1 - r} .$ si225_e

The sum to infinity of a GP can be found if |r| < 1 and is given by

$S_{\infty} = \frac{a}{1 - r} .$ $S_{\infty} = \frac{a}{1 - r} .$

7. The binomial expansion gives

$\begin{array}{l} {(a + b)}^{n} = a^{n} + n a^{n - 1} b + \frac{n (n - 1)}{2!} a^{n - 2} b^{2} \\ + \frac{n (n - 1) (n - 2)}{3!} a^{n - 3} b^{3} + \dots \end{array}$ $\begin{array}{l} {(a + b)}^{n} = a^{n} + n a^{n - 1} b + \frac{n (n - 1)}{2!} a^{n - 2} b^{2} \\ + \frac{n (n - 1) (n - 2)}{3!} a^{n - 3} b^{3} + \dots \end{array}$

si227_e

where n can be a whole number or a fraction.

8. The Maclaurin series is a series expansion of a function about x = 0. If a function f (x) is defined for values of x around x = 0, within some radius R, that is, for − R < x < R (or |x| < R) and if all its derivatives are defined then:

$\begin{array}{l} f (x) = f (0) + f^{'} (0) x + \frac{f^{″} (0)}{2!} x^{2} + \frac{f^{‴} (0)}{3!} x^{3} \\ + \dots + \frac{f^{(n)} (0)}{n!} x^{n} + \dots \end{array}$ $\begin{array}{l} f (x) = f (0) + f^{'} (0) x + \frac{f^{″} (0)}{2!} x^{2} + \frac{f^{‴} (0)}{3!} x^{3} \\ + \dots + \frac{f^{(n)} (0)}{n!} x^{n} + \dots \end{array}$

si228_e

This gives a power series with coefficient sequence:

$a_{n} = \frac{f^{(n)} (0)}{n!}$ $a_{n} = \frac{f^{(n)} (0)}{n!}$

si229_e

where f⁽ⁿ⁾(0) is found by calculating the nth derivative of f (x) with respect to x and then substituting x = 0.

9. Maclaurin's series is just a special case of Taylor series. A Taylor series is a series expansion of a function not necessarily taken around x = 0. If a function f(x) is defined for values of x around x = a, within some radius R, that is, for a−R < x < a+R (or |x−a| < R) and if all its derivatives are defined, then:

$\begin{array}{l} f (x) = f (a) + f^{'} (a) (x - a) + \frac{f^{″} (a)}{2!} {(x - a)}^{2} \\ + \frac{f^{‴} (a)}{3!} {(x - a)}^{3} + \dots + \frac{f^{(n)} (a)}{n!} {(x - a)}^{n} + \dots \end{array}$ $\begin{array}{l} f (x) = f (a) + f^{'} (a) (x - a) + \frac{f^{″} (a)}{2!} {(x - a)}^{2} \\ + \frac{f^{‴} (a)}{3!} {(x - a)}^{3} + \dots + \frac{f^{(n)} (a)}{n!} {(x - a)}^{n} + \dots \end{array}$

si230_e

or, substituting x = a + h, where h is usually considered to be a small value, we get

$\begin{array}{l} f (a + h) = f (a) + f^{'} (a) h + \frac{f^{″} (a)}{2!} h^{2} + \frac{f^{‴} (a)}{3!} h^{3} \\ + \dots + \frac{f^{(n)} (a)}{n!} h^{n} + \dots . \end{array}$ $\begin{array}{l} f (a + h) = f (a) + f^{'} (a) h + \frac{f^{″} (a)}{2!} h^{2} + \frac{f^{‴} (a)}{3!} h^{3} \\ + \dots + \frac{f^{(n)} (a)}{n!} h^{n} + \dots . \end{array}$

si231_e

10. L'Hopital's rule is a way of finding the limit of a function at a point where it is undetermined (i.e. it gives 0/0 at the point). The

rule states that if a function f (x) = g (x) / h (x) is indeterminate at x = a then:

$lim_{x \to a} \frac{g (x)}{h (x)} = lim_{x \to a} \frac{g^{'} (x)}{h^{'} (x)} .$ $lim_{x \to a} \frac{g (x)}{h (x)} = lim_{x \to a} \frac{g^{'} (x)}{h^{'} (x)} .$

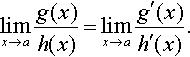
si232_e

If g′ (a) / h′ (a) is defined, we can then use

$lim_{x \to a} \frac{g^{'} (x)}{h^{'} (x)} = \frac{g^{'} (a)}{h^{'} (a)}$ $lim_{x \to a} \frac{g^{'} (x)}{h^{'} (x)} = \frac{g^{'} (a)}{h^{'} (a)}$

si233_e

and if g′ (a) / h′ (a) is indeterminate, we can use the rule again.

11. To test if a sequence tends to a limit follow the following procedure:

(a) Choose a number of significant figures.

(b) Write all the terms in the sequence to that number of significant figures.

(c) The sequence tends to a limit if the terms in the sequence, when expressed to the agreed number of significant figures becomes constant, that is, do not change after some value of n.

This procedure must theoretically work for any chosen number of significant figures.

12. The algorithm for solving an equation using Newton–Raphson method can be described as

Step 1: Take an equation and write it in the form f (x) = 0.

Step 2: Take a guess at a solution

Step 3: Calculate a new value for x using

$x \leftarrow x - \frac{f (x)}{f^{'} (x)}$ $x \leftarrow x - \frac{f (x)}{f^{'} (x)}$

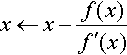
si234_e

Step 4: Repeat Step 3 until some convergence criterion has been satisfied or until it is decided that the method has failed to find a solution.

13. Convergence criteria can either be based on the testing the size of the absolute error or the relative absolute error. To find the limit of a convergent sequence defined by a recurrence relation, correct to three decimal places, we can test for |x_n− x_n−1| < 0.0005 and to be correct to three significant figures we could test for |x_n − x_n−1| < 0.0005|x_n|. It is also necessary to put a limit on the number of iterations of some algorithm to check for the eventuality that the sequence fails to converge (is divergent).

12.10 Exercises

12.1. Find the next three terms in the following sequences. In each case, express the rule for the sequence as a recurrence relation.

(a) −3, 1, 5, 9, 13, 17, …

(b) 8, 4, 2, 1, 0.5, …

(d) 6, −6, 6, −6, …

(e) 10, 8, 6, 4, …

(f) 1, 2, 4, 7, 11, 16, 22, …

(g) 1, 3, 6, 10, 15, …

12.2. Given the following definitions of sequences write out the first five terms

(a) a_n = 3n − 1

(b) x_n= 720/n

(d) a_n+1 = a_n+ 2; a_l = 6

(e) a_n+1 = 3a_n; a₁ = 2

(f) a_n+1 = −2a_n; a_l = −1

(g) b_n+1 = 2b_n − b_n−1; b₁ = 1/2, b₂ = 1

(h) Δy_n = 3; y₀ = 2

(i) Δy_n = 2y_n; y₀ = 1.

12.3. Express the following using sigma notation

(a) $1 + x + x^{2} + x^{3} + \cdot \cdot \cdot + x^{10}$ $1 + x + x^{2} + x^{3} + \cdot \cdot \cdot + x^{10}$

(b) $- 2 + 4 - 8 + 16 - \cdot ? \cdot ? \cdot + 256$ $- 2 + 4 - 8 + 16 - \cdot ? \cdot ? \cdot + 256$

(d) $- \frac{1}{3} + \frac{1}{9} - \frac{1}{27} + \dots - \frac{1}{6561}$ $- \frac{1}{3} + \frac{1}{9} - \frac{1}{27} + \dots - \frac{1}{6561}$

(e) $\frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \frac{1}{25} + \frac{1}{36} + \dots + \frac{1}{100}$ $\frac{1}{4} + \frac{1}{9} + \frac{1}{16} + \frac{1}{25} + \frac{1}{36} + \dots + \frac{1}{100}$

(f) $- 4 - 1 - \frac{1}{4} - \frac{1}{16} - \dots - \frac{1}{4096} .$ $- 4 - 1 - \frac{1}{4} - \frac{1}{16} - \dots - \frac{1}{4096} .$

12.4. Sketch the following functions and give the first 10 terms of their sequence representation (t ≥ 0) at the sampling interval T given:

(a) f (t) = sin(2t), T = 0.1

(b) f (t) = cos(30t), T = 0.01

$f (t) = {\begin{array}{l} 2 t & 0 \leq t \leq 4 \\ 16 - 2 t & 4 < t \leq 12 \\ 2 t - 32 & 12 < t < 16 \end{array}$ $f (t) = {\begin{array}{l} 2 t & 0 \leq t \leq 4 \\ 16 - 2 t & 4 < t \leq 12 \\ 2 t - 32 & 12 < t < 16 \end{array}$

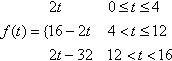
si241_e

with sample interval T = 1.

(d) The square wave of period 2 given for 0 < t < 2 by

$f (t) = {\begin{array}{l} 1 & 0 \leq t < 1 \\ - 1 & 1 \leq t < 2 \end{array}$ $f (t) = {\begin{array}{l} 1 & 0 \leq t < 1 \\ - 1 & 1 \leq t < 2 \end{array}$

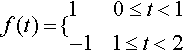
si242_e

with a sampling interval of T = 0.25.

12.5. The following are arithmetic progressions. Find the fifth, tenth, and general term of the sequence in each case.

(a) 6, 10, 14, …

(b) 3, 2.5, 2, …

12.6. a_n is an arithmetic progression. Given the terms indicated, find the general term and find the sum of the first 20 terms in each case:

(a) a₅ = 6, a₁₀ = 26

(b) a₇ = −2, a₁₆ = 2.5

12.7. The sum of the first 10 terms of an arithmetic progression is 50 and the first term is 2. Find the common difference and the general term and list the first six terms of the sequence.

12.8 How many terms are required in the arithmetic series 2 + 4 + 6 + 8 + … to make a sum of 1056?

12.9 The following are geometric progressions. Find the fourth, eighth, and general term in each case:

(a) 1, 2, 4, …

(b) 1/3, 1/12, 1/48, …

(d) 15, 18.75, 23.4375, …

12.10. a_n is a geometric progression. Given the terms indicated, find the general term and find the sum of the first 8 terms in each case.

(a) a₃ = 8, a₆ = 1000

(b) a₆ = 54, a₉ = −486

12.11. How many terms are required in the geometric series 8 + 4 + 2 + … to make a sum of 15.9375?

12.12. A loan of €40 000 is repaid by annual instalments of €5000, except in the final year when the outstanding debt (if less than €5000) is repaid. Interest is charged at 10% per year, calculated at the end of each year on the outstanding amount of the debt. The first repayment is 1 year after the loan was taken out. Calculate the number of years required to repay the loan.

12.13. Evaluate the following

(a) $Σ_{n = 1}^{n = 4} 2^{n}$ $Σ_{n = 1}^{n = 4} 2^{n}$

(b) $Σ_{r = 0}^{r = 8} \frac{1}{2^{r}}$ $Σ_{r = 0}^{r = 8} \frac{1}{2^{r}}$

(c) ${Σ_{j = 1}^{j = 10} {(- 1)}^{j} (\frac{1}{3})}^{j - 2} .$ ${Σ_{j = 1}^{j = 10} {(- 1)}^{j} (\frac{1}{3})}^{j - 2} .$

12.14. Find the sum of the first n terms of the following:

(a) $1 + z + z^{2} + z^{3} + \cdot \cdot \cdot$ $1 + z + z^{2} + z^{3} + \cdot \cdot \cdot$

(b) $1 - y^{2} + y^{4} - \cdot \cdot \cdot$ $1 - y^{2} + y^{4} - \cdot \cdot \cdot$

12.15. State whether the following series are convergent and if they are find the sum to infinity.

(a) $2 + 1 + \frac{1}{2} + \frac{1}{4} + \dots$ $2 + 1 + \frac{1}{2} + \frac{1}{4} + \dots$

(b) $3 + 0 - 3 - 6 \cdot \cdot \cdot$ $3 + 0 - 3 - 6 \cdot \cdot \cdot$

(d) $0.3 + 0.03 + 0.003 \cdot \cdot \cdot$ $0.3 + 0.03 + 0.003 \cdot \cdot \cdot$

12.16. Find the following recurring decimals as fractions:

(a) $0 . \dot{4}$ $0 . \dot{4}$

(b) $0.1 \dot{6}$ $0.1 \dot{6}$

12.17. Expand the following expressions

(a) ${(1 + \frac{1}{2} x)}^{3}$ ${(1 + \frac{1}{2} x)}^{3}$

(b) ${(1 - x)}^{4}$ ${(1 - x)}^{4}$

(d) ${(1 - 2 y)}^{4}$ ${(1 - 2 y)}^{4}$

(e) ${(1 + x)}^{8}$ ${(1 + x)}^{8}$

(f) ${(2 x + 1)}^{3}$ ${(2 x + 1)}^{3}$

(g) ${(2 a + b)}^{3}$ ${(2 a + b)}^{3}$

(h) ${(x + (1 / x))}^{7}$ ${(x + (1 / x))}^{7}$

(i) ${(a - 2 b)}^{4}$ ${(a - 2 b)}^{4}$

12.18. Find the following using the expansion indicated:

(a) (1.1)³ using (1 + 0.1)³

(b) (0.9)⁴ using (1 – 0.1)⁴

12.19. Give the first 4 terms in the binomial expansion of the following:

(a) ${(1 + 2 x)}^{5}$ ${(1 + 2 x)}^{5}$

(b) ${(1 - 3 x)}^{8}$ ${(1 - 3 x)}^{8}$

(d) ${(1 + \frac{1}{2} x)}^{16}$ ${(1 + \frac{1}{2} x)}^{16}$

(e) ${(1 - x)}^{6}$ ${(1 - x)}^{6}$

(f) ${(1 - 2 x)}^{5}$ ${(1 - 2 x)}^{5}$

12.20. Use sin(5θ) = Im(e^j5θ) = Im((cos(θ)+j sin(θ))⁵) to find sin(5θ) in terms of powers of cos(θ) and sin(θ).

12.21. Find the real and imaginary parts of the following:

(a) (1 − j) ⁶

(b) (1 + j2)⁴

12.22. Use a binomial expansion to find the following correct to four decimal places:

(a) (0.99)⁸

(b) (1.01)⁷

12.23. Find the first 4 non-zero terms in a power series expansion of the following functions and state for what values of x they are valid in each case.

(a) cos(x)

(b) cosh(x)

(d) (l+x)^1.5

(e) (1 + x)⁻².

12.24. Find the first 4 non-zero terms in a power series expansion for the following functions:

(a) cos²(x)

(b) tan⁻¹(x)

(d) (1 − x)^1.5/(1 + x).

12.25. Using a series expansion find the following correct to 4 significant figures:

(a) $\sqrt{1.05}$ $\sqrt{1.05}$

(b) ${tan}^{- 1} (0.1)$ ${tan}^{- 1} (0.1)$

(d) $1 / \sqrt{1.06}$ $1 / \sqrt{1.06}$

12.26. Using a series expansion and the given value of the function at x = a, evaluate the following correct to four significant figures:

(a) $cos (7 π / 16) using cos (π / 2) = 0,$ $cos (7 π / 16) using cos (π / 2) = 0,$ ,

(b) $\sqrt{4.02} using \sqrt{4} = 2 .$ $\sqrt{4.02} using \sqrt{4} = 2 .$

12.27. Find the following limits:

(a) $lim_{x \to 2} ((x^{2} - x - 2) / (4 x^{3} - 4 x - 7 x - 2))$ $lim_{x \to 2} ((x^{2} - x - 2) / (4 x^{3} - 4 x - 7 x - 2))$

(b) $lim_{x \to 0} (x^{3} / (x - sin (x)))$ $lim_{x \to 0} (x^{3} / (x - sin (x)))$

(c) $lim_{x \to - 3} ((x^{2} + 6 x + 9) / (4 x^{2} + 11 x - 3))$ $lim_{x \to - 3} ((x^{2} + 6 x + 9) / (4 x^{2} + 11 x - 3))$

(d) $lim_{x \to π / 2} ((π / 2 - x) / cos (x))$ $lim_{x \to π / 2} ((π / 2 - x) / cos (x))$

(e) $lim_{x \to 0} (tan (x)) / x)$ $lim_{x \to 0} (tan (x)) / x)$

(f) $lim_{x \to 0} (sin (x - 2) / (x^{2} - 4 x + 4)) .$ $lim_{x \to 0} (sin (x - 2) / (x^{2} - 4 x + 4)) .$

12.28. Use the Newton–Raphson method to find a solution to the following equations correct to six significant figures:

(a) $x^{3} - 2 x = 1$ $x^{3} - 2 x = 1$

(b) $x^{4} = 5$ $x^{4} = 5$

12.29. Suggest a test for convergence that could be used in a computer program so that the limit of a sequence, defined by some recurrence relation, could be assumed to be correct to

(a) six decimal places,

(b) six significant figures.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 12.7 Limits and convergence

Create new playlist

Sign In

Sign Up

L'Hopital's rule

Example 12.32

Example 12.33

12.7 Limits and convergence

12.8 Newton–Raphson method for solving equations

Example 12.34

Example 12.35

The convergence criterion

Example 12.36

Example 12.37

Divergence

12.9 Summary

12.10 Exercises

Table of Contents for
12.7 Limits and convergence