2

Functions and their graphs

2.1 Introduction

The ability to produce a picture of a problem is an important step towards solving it. From the graph of a function, y = f (x), we are able to predict such things as the number of solutions to the equation f(x) = 0, regions over which it is increasing or decreasing, and the points where it is not defined.

Recognizing the shape of functions is an important and useful skill. Oscilloscopes give a graphical representation of voltage against time, from which we may be able to predict an expression for the voltage. The increasing use of signal processing means that many problems involve analysing how functions of time are effected by passing through some mechanical or electrical system.

In order to draw graphs of a large number of functions, we need only remember a few key graphs and appreciate simple ideas about transformations. A sketch of a graph is one which is not necessarily drawn strictly to scale but shows its important features. We shall start by looking at special properties of the straight line (linear function) and the quadratic. Then we look at the graphs of y = x, y = x2, y = 1/x, y = axand how to transform these graphs to get graphs of functions like y = 4 x − 2, y = (x − 2)2, y = 3/x, and y = a−x.

2.2 The straight line: y = mx + c

y = mx + c is called a linear function because its graph is a straight line. Notice that there are only two terms in the function; the x term, mx, where m is called the coefficient of x and c which is the constant term. m and c have special significance. m is the gradient, or the slope, of the line and c is the value of y when x = 0, that is, when the graph crosses the y-axis. This graph is shown in Figure 2.1(a) and two particular examples shown in Figure 2.1(b) and (c).

f02-01-9780750658553
Figure 2.1 (a) The graph of the function y = mx + c. m is the slope of the line, if m is positive then travelling from left to right along the line of the function is an uphill climb, if m is negative then the journey is downhill. The constant c is where the graph crosses the y-axis. (b) m = 2 and c = 3 (c) m = −1 and c = 2.

The gradient of a straight line

The gradient gives an idea of how steep the climb is as we travel along the line of the graph. If the gradient is positive then we are travelling uphill as we move from left to right and if the gradient is negative then we are travelling downhill. If the gradient is zero then we are on flat ground. The gradient gives the amount that y increases when x increases by 1 unit. A straight line always has the same slope at whatever point it is measured. To show that in the expression y = mx + c, m is the gradient, we begin with a couple of examples as in Figure 2.1(b) and (c)

In Figure 2.1(b), we have the graph of y = 2x + 3. Take any two values of x which differ by 1 unit, for example, x = 0 and x = 1. When x = 0, y = 2 × 0 + 3 = 3 and when x = 1, y = 2 × 1 + 3 = 5. The increase in y is 5 – 3 = 2, and this is the same as the coefficient of x in the function expression.

In Figure 2.1(c), we see the graph of y = −x + 2. Take any two values of x which differ by 1 unit, for example, x = 1 and x = 2. When x = 1,y = −(1) + 2 = 1 and when x = 2,y = −(2) + 2 = 0. The increase in y is 0–1 = −1 and this is the same as the coefficient of x in the function expression.

In the general case, y = mx + c, take any two values of x which differ by 1 unit, for example, x = x0 and x = x0 + 1. When x = x0, y = mx0+c and when x = x0 + 1, y = m(x + 1) + c = mx + m + c. The increase in y is mx + m + c − (mx + c) = m.

We know that every time x increases by 1 unit y increases by m. However, we do not need to always consider an increase of exactly 1 unit in x. The gradient gives the ratio of the increase in y to the increase in x. Therefore, if we only have a graph and we need to find the gradient then we can use any two points that lie on the line.

To find the gradient of the line take any two points on the line (x1, y1) and (x2, y2).

The?gradient=change?in?ychange?in?x=y2−y1x2−x1

si4_e

Example 2.1

Find the gradient of the lines given in Figure 2.2(a)–(c) and the equation for the line in each case.

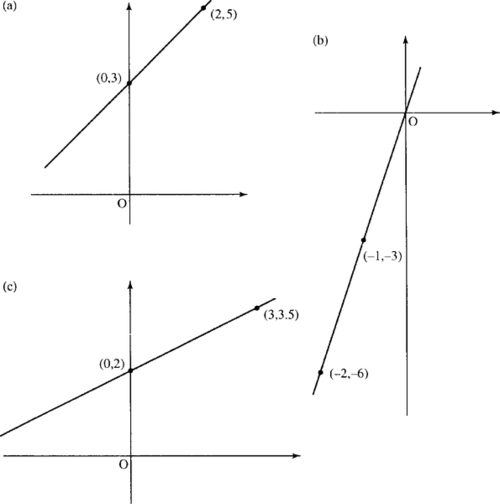
f02-02-9780750658553
Figure 2.2 Graphs for Example 2.1.

Solution

(a) We are given the coordinates of two points that lie on the straight line in Figure 2.2(a) as (0,3) and (2,5),

gradient=change?in?ychange?in?x=5−32−0=22=1.

si5_e

To find the constant term in the expression y = mx + c, we find the value of y when the line crosses the y-axis. From the graph this is 3, so the equation is y = mx + c where m = 1 and c = 3, giving

y=x+3

si6_e

(b) Two points that lie on the line in Figure 2.2(b) are (−1, −3) and (−2, −6). These are found by measuring the x and y values for some points on the line.

gradient=change?in?ychange?in?x=−6−(−3)−2−(−1)=−3−1=3.

si7_e

To find the constant term in the expression y = mx + c, we find the value of y when the line crosses the y-axis. From the graph this is 0, so the equation is y = mx + c where m = 3 and c = 0 giving y = 3x

(c) Two points that lie on the line in Figure 2.2(c) are (0,2) and (3,3.5).

gradient=change?in?ychange?in?x=3.5−23−0=1.53=0.5

si8_e


To find the constant term in the expression y = mx + c, we find the value of y when the line crosses the y-axis. From the graph this is 2, so the equation is y = mx + c where m = 0.5 and c = 2 giving

y=0.5x+2

si9_e

Finding the gradient from the equation for the line

To find the gradient from the equation of the line we look for the value of m, the number multiplying x in the equation. The constant term gives the value of y when the graph crosses the y-axis, that is, when x = 0.

Example 2.2

Find the gradient and the value of y when x = 0 for the following lines:

(a)(c)y=2x+3,x−2y=4,(b)(d)3x−4y=2,x−12=1−y3.

si10_e

Solution

(a) In the equation y = 2x + 3, the value of m, the gradient, is 2 as this is the coefficient of x. c = 3 which is the value of y when the graph crosses the y-axis, that is, when x = 0.

(b) In the equation 3x − 4 y = 2, we rewrite the equation with y as the subject of the formula in order to find the value of m and c.

3x−4y=2⇔⇔⇔⇔3x=2+4y3x−2=4y3x4−24=yy=3x4−12

si11_e

We can see, by comparing the expression with y = mx + c, that m, the gradient, is 3/4 and c = −1/2.

(c) Write y as the subject of the formula:

x−2y=4⇔⇔⇔⇔x=4+2yx−4=2y2y=x−4y=x2−2

si12_e

We can see, by comparing the expression with y = mx + c, that m, the gradient, is 1/2 and c = −2.

(d) Write y as the subject of the formula

x−12=1−y3⇔⇔⇔⇔x2−12=1−y33x2−32=3−yy=3−(3x2−32)y=−3x2+92

si13_e

We can see, by comparing the expression with y = mx + c, that m, the gradient, is − 3 /2 and c = 9/2.

Finding the equation of a line which goes through two points

Supposing we have been given two points, (x1, y1) and (x2, y2), which lie on a line and we want to find the equation of that line. We already found that the gradient of the line is given by:

The?gradient=change?in?ychange?in?x=y2−y1x2−x1

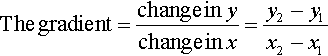
si14_e

We know that the equation of a line is of the form y = mx + c, but we would like to express the equation just in terms of the two variables, x and y, and the known points which the line passes through, (x1, y1) and (x2, y2). To do this we use the fact that a line is of constant gradient. That means that for any point (x, y), the gradient between (x, y) and the point (x1, y1) must be the same as the gradient between (x1, y1) and the point (x2, y2). This gives:

y−y1x−x1=y2−y1x2−x1

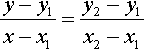
si15_e

providing that y2 ≠ y1, we can rearrange this equation as:

y−y1y2−y1=x−x1x2−x1

si16_e

Note that if y2 = y1 and we have chosen two different points on the line, that is, x2 ≠ x1 then y is a constant and the equation of the line will be y = y1.

Example 2.3

(a) Find the equation of a line through the points (2,4) and (0,6).

(b) Find the equation of a line through the points (1, −6) and (5, −6).

Solution

(a) To find the equation of a line through the points (2,4) and (0,6) we use

y−y1y2−y1=x−x1x2−x1and?(x1,y1)=(2,4)and?(x2,y2)=(0,6).

si17_e

This gives

y−46−4=x−20−2⇔????y−42=−x−22⇔????y−4=2−x⇔????y=−x+6

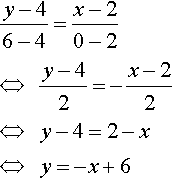
si18_e

Check: Check that this is the correct equation by substituting the points (2,4) and (0,6) into the equation y = −x + 6. (2,4) gives 4 = −2 + 6 ⇔4 = 4, which is true; (0,6) gives 6 = −0 + 6, which is true.

This shows that y = −x + 6 is the equation of a straight line which goes through the points (2,4) and (0,6).

(b) To find the equation of a line through the points (1, −6) and (5, −6) we try to use (y − y1) / (y2 − y1) = (x − x1) / (x2 − x1) with (x1, y1) = (1, −6) and (x2, y2) = (5, −6) but find that, because y2 = y1, the substitution would result in a division by 0, which is undefined. We note that y has constant value and therefore the equation of the line is:

y=−6.

si19_e

Sketching a straight line graph

The quickest way to sketch a straight line graph is to find the points where it crosses the axes. However, any two points on the graph can be used and sometimes it is more convenient to find other points.

Example 2.4

(a) Sketch the graph of y = 4x − 2.

To find where the graph crosses the y-axis, substitute x = 0 into the equation of the line:

y=4(0)−2=−2.

si20_e

This means that the graph passes through the point (0,−2). To find where the graph crosses the x-axis, substitute y = 0, that is,

4x−2=0⇔?????4x=2⇔?????x=24=0.5.

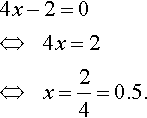
si21_e

Therefore, the graph passes through (0.5, 0).

Mark the points (0,2) and (0.5,0), on the x- and y-axes and join the two points. This is done in Figure 2.3(a).

f02-03-9780750658553
Figure 2.3 (a) The graph of y = 4x − 2. (b) The graph of y = −4x.

(b) Sketch the graph of y = −4x When x = 0 we get y = 0, that is the graph goes through the point (0,0). In this case, as the graph passes through the origin, we need to choose a different value for x for the second point. Taking x = 2 gives y = −8, so another point is (2, −8). These points on marked on the graph and joined to give the graph as in Figure 2.3(b).

2.3 The quadratic function: y = ax2+bx+c

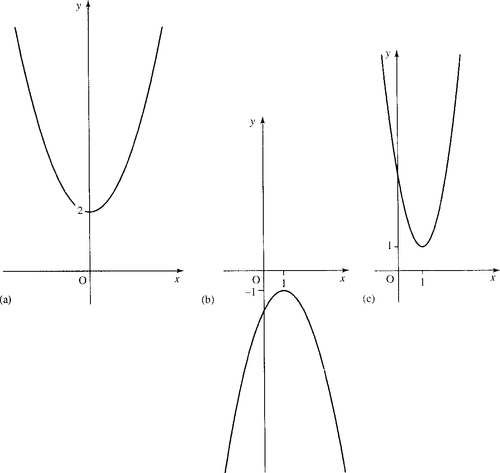
y = ax2+ bx + c is a general way of writing a function in which the highest power of x is a squared term. This is called the quadratic function and its graph is called a parabola as shown in Figure 2.4.

f02-04-9780750658553
Figure 2.4 (a) The function y = ax2+ bx + c. (a) Case 1 where there are 2 solutions to f(x) = 0. (b) Case 2 where there is only one solution to f(x) = 0. (c) Case 3, where there are no real solutions to f(x) = 0.

All the graphs, in this figure, cross the y-axis at (0, c). To find where they cross the x-axis can be more difficult. These values, where f(x) = 0, are called the roots of the equation. There is a quick way to discover whether the function crosses the x-axis, only touches the x-axis, or does not cross or touch it. In the latter case there are no solutions to the equation f(x) = 0. The three possibilities are given in Figure 2.4.

Crossing the x-axis

The function y = ax2+ bx + c crosses the x-axis when y = 0, that is, when ax2+bx+c = 0. The solutions to ax2+bx+c = 0 are examined in the Background Mathematics Notes available on the companion website for this book and are given by the formula

x=−b±b2−4ac√2a

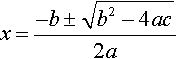
si22_e

From the graph, we can see there are three possibilities:

1. In Figure 2.4(a) where there are two solutions, that is, the graph crosses the x-axis for two values of x. For this to happen, the square root part of the formula above must be greater than zero:

b2−4ac>0

si23_e

Examples are given in Figure 2.5.

f02-05-9780750658553
Figure 2.5 Three quadratic functions with two roots to the equation f (x) = 0. Each satisfies b2− 4ac > 0. (a) y = 2x2− 3, a = 2, b = 0, c = −3, b2− 4ac = 0 − 4(2) (−3) = 24. (b) y = −x2+ 5, a = −1, b = 0, c = 5, b2− 4ac = 0 − 4(−1)(5) = 20.(c) Y = −3(x − 2)2 + 1 ⇔ y = −3x2+ 12x − 11, a = −3, b = 12 c = − 11 b2− 4ac = (12)2–4(−3) (−11) = 144–132 = 12.

2. Only one unique solution, as in Figure 2.4(b). The graph touches the x-axis in one place only. For this to happen, the square root part of the formula must be exactly 0. Examples of this are given in Figure 2.6.

f02-06-9780750658553
Figure 2.6 Quadratic functions with only one unique root of the equation f (x) = 0. Each satisfies b2− 4ac = 0. (a) y = x2− 4x + 4, a = 1, b = −4, c = 4, b2− 4ac = (−4)2−4(1)(4) = 16–16 = 0. (b) Y = −3x2− 12x − 12, a = −3, b = −12, c = −12, b2− 4ac = (−12)2–4(−3)(−12) = 144–144 = 0. (c) y = x2, a = 1, b = 0 c = 0 b2− 4ac = (0)2− 4(1)(0) = 0–0 = 0.

3. No real solutions, that is, the graph does not cross the x-axis. Examples of these are given in Figure 2.7.

f02-07-9780750658553
Figure 2.7 Quadratic functions with no real roots to the equation f (x) = 0. In each case b2− 4ac < 0. (a) y = x2 + 2, a = 1, b = 0 c = 2 b2− 4ac = (0)2− 4(1)(2) = 0–8 = −8. (b) y = −x2 + 2x − 2, a = −1, b = 2, c = −2, b2− 4ac = (2)2− 4(−1)(−2) = 4–8 = −4. (c) y = 3x2− 6x + 4, a = 3, b = −6, c = 4, b2− 4ac = (−6)2–4(3)(4) = 36–48 = −12.

2.4 The function y = 1/x

The function y = 1/x has the graph as in Figure 2.8. This is called a hyperbola. Notice that the domain of f(x) = 1/x does not include x = 0. The graph does not cross the x-axis so there are no solutions to 1/x = 0.

f02-08-9780750658553
Figure 2.8 Graph of the hyperbolic function y = 1/x.

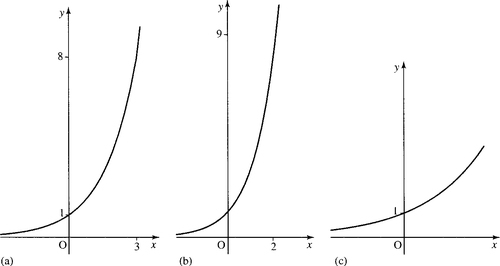
2.5 The functions y = ax

Graphs of exponential functions, y = ax, are shown in Figure 2.9. The functions have the same shape for all a > 1. Notice that the function is always positive and the graph does not cross the x-axis so there are no solutions to the equation ax= 0.

f02-09-9780750658553
Figure 2.9 Graphs of functions y = ax: (a) y = 2x; (b) y = 3x; (c) y = (1.5)x.

2.6 Graph sketching using simple transformations

One way of sketching graphs is to remember the graphs of simple functions and to translate, reflect or scale those graphs to get graphs of other functions. We begin with the graphs below as given in Figure 2.10.

f02-10-9780750658553
Figure 2.10 To sketch graphs using transformations we begin with known graphs. In the rest of this section we use: (a) y = x; (b) y = x2; (c) y = x3; (d) y = 1/x; (e) y = ax.

The translation x arrow x + a

If we have the graph of y = f(x), then the graph of y = f(x + a) is found by translating the graph of y = f(x) a units to the left. Examples are given in Figure 2.11.

f02-11-9780750658553
Figure 2.11 Translations x arrow x + a. (a) (i) y = 1/x; (ii) y = 1 I(x + 2). Here x has been replaced by x + 2 translating the graph 2 units to the left. (b) (i) Y = x2; (ii) y = (x − 3)2, x has been replaced by x − 3 translating the graph 3 units to the right.

The translation f(x) arrow (x) + A

Adding A on to the function value leads to a translation of A units upwards. Examples are given in Figure 2.12.

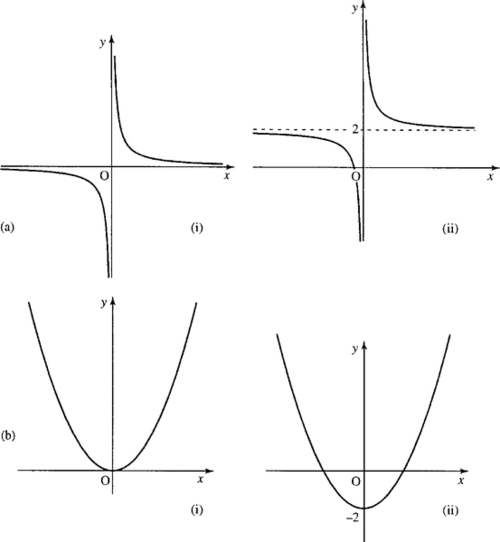
f02-12-9780750658553
Figure 2.12 Translations f(x) arrow f(x) + A. (a) y = 1/x; (ii) y = 1/x + 2. Here the function value has been increased by 2 translating the graph 2 units upwards. (b) (i) y = x2; (ii) y = x2− 2. The function value has had 2 subtracted from it, translating the graph 2 units downwards.

Reflection about the y-axis, x arrow −x

Replacing x by −x in the function has the effect of reflecting the graph in the y-axis – that is, as though a mirror has been placed along the axis and only the reflection can be seen. Examples are given in Figure 2.13.

f02-13-9780750658553
Figure 2.13 Reflections x arrow −x. (a) (i) y = ax, a > 1; (ii) y = a−x, x has been replaced by −x to get the second function. This has the effect of reflecting the graph in the y-axis. (b) (i) y = (x/2) + (1/2); (N) y = −(x/2) + (1/2), x has been replaced by −x, reflecting the graph in the y-axis.

Reflection about the x axis, f(x) arrow −f(x)

To find the graph of y = − f(x), reflect the graph of y = f(x) about the x-axis. Examples are given in Figure 2.14.

f02-14-9780750658553
Figure 2.14 Reflections f(x) arrow −f(x). (a) (i) y = x2; (ii) y = −x2. The function value has been multiplied by −1 turning the graph upside down (reflection in the x-axis). (b) (i) y = 2x; (ii) y = −2x. The second function has been multiplied by −1 turning the graph upside down.

Scaling along the x-axis, x arrow ax

Multiplying the values of x by a number, a, has the effect of: squashing the graph horizontally if a > 1 or stretching the graph horizontally if o < a < 1. Examples are given in Figure 2.15.

f02-15-9780750658553
Figure 2.15 Scalings x arrow ax. (a) (i) y = x2; (ii) y = [(1/2)x]2; (iii) y = (2x)2. The second function has x replaced by (1/2)x which has stretched the graph horizontally (the multiplication factor is between 0 and 1). The third function has replaced x by 2x, which has squashed the graph horizontally (the multiplication factor is greater than 1). (b) (i) y = 2x; (ii) y = 2(1/2x); (iii) y = 22x. The second function has replaced x by (1/2)x which has stretched the graph horizontally. The third function has x replaced by 2x which has squashed the graph horizontally.

Scaling along the y-axis, f(x) arrow Af(x)

Multiplying the function value by a number A has the effect of stretching the graph vertically if A > 1, or squashing the graph vertically if 0 < A < 1. Examples are given in Figure 2.16.

f02-16-9780750658553
Figure 2.16 Scalings f(x) arrow Af(x). (a) y = 1/(x + 2); (b) y = 2/(x + 2) (c) y = 1/[3(x + 2)]. The second graph has the function values multiplied by 2 stretching the graph vertically. The third graph has function values multiplied by 1/3 squashing the graph vertically.

Reflecting in the line y = x

If the graph of a function y = f(x) is reflected in the line y = x, then it will give the graph of the inverse relation. Examples are given in Figure 2.17.

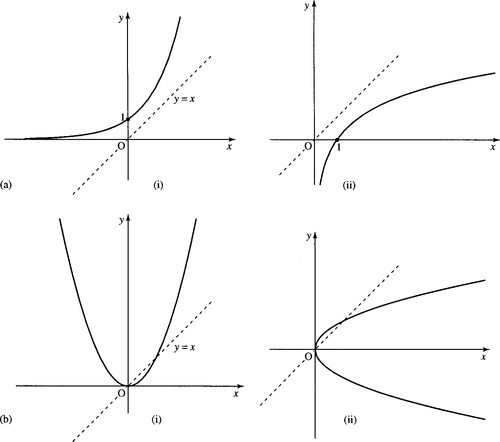
f02-17-9780750658553
Figure 2.17 Reflections in the line y = x produce the inverse relation. (a) (i) y = 2x; (ii) y = log2(x). The second graph is obtained from the first by reflecting in the dotted line y = x. The inverse is a function as there is only one value of y for each value of x. (b) (i) y = x2; (ii) y=±X−−√si1_e. The second graph is found by reflecting the first graph in the line y = x. Notice that y=±X−−√si2_e is not a function as there is more that one possible value of y for each value of x > 0.

In Chapter 1, we defined the inverse function as taking any image back to its original value. Check this with the graph of y = 2xin Figure 2.17(a): x = 1 gives y = 2. In the inverse function, y = log2 (x), substitute 2, which gives the result of 1, which is back to the original value.

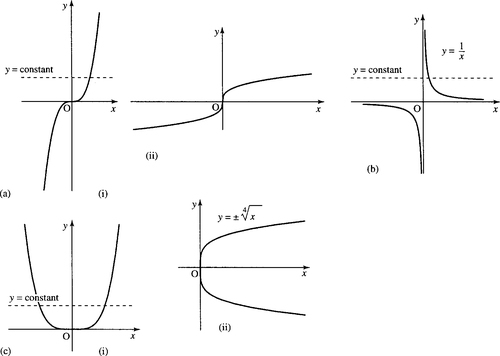
However, the inverse of y = x2, y ± x−−√si24_e, shown in Figure 2.17(b), is not a function as there is more than one y value for a single value of x. To understand this problem more fully, perform the following experiment. On a calculator enter −2 and square it (x2) giving 4. Now take the square root. This gives the answer 2, which is not the number we first started with, and hence we can see that the square root is not a true inverse of squaring. However, we get away with calling it the inverse because it works if only positive values of x are considered. To test if the inverse of any function exists, draw a line along any value of y = constant. If, wherever the line is drawn, there is ever more than one x value which gives the same value of y then the function has no inverse function. In this situation, the function is called a ‘many-to-one’ function. Only ‘one-to-one’ functions have inverses. Figure 2.18 has examples of functions with an explanation of whether they are ‘one-to-one’ or ‘many-to-one’.

f02-18-9780750658553
Figure 2.18 (a) (i) y = x3. This function has only one x value for each value of y as any line y = constant only cuts the graph once. In this case, the function is one-to-one and it has an inverse function (ii) y = Tx is the inverse function of y = x3. (b) Y = 1/ x, x i = − 0, has only one x value for each value of y as any line y = constant only cuts the graph once. It therefore is one-to-one and has an inverse function – in fact, it is its own inverse! (to see this reflect it in the line y = x and we get the same graph after the reflection). (c) (i) y = x4. This function has two values of x for each value of y when y is positive (e.g. the line y = 16 cuts the graph twice at x = 2 and at x = −2). This shows that there is no inverse function as the function is many-to-one. (ii) The inverse relation y=±X−−√4si3_e.

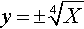2.7 The modulus function, y = |x| or y = abs(x)

The modulus function y = |x|, often written as y = abs(x) (short for the absolute value of x) is defined by

y={x?x≥0(x?positive?or?zero)−x?x<0(x?negative)

si25_e

The output from the modulus function is always a positive number or zero.

Example 2.5

Find |−3|. Here x = −3, which is negative, therefore

y=−x=−(−3)=+3.

si26_e

An alternative way of thinking of it is to remember that the modulus is always positive, or zero, so simply replacing any negative sign by a positive one will give a number's modulus or absolute value.

|−5|=5,????|−4|=4,?????|5|=5,????|4|=4.

si27_e

The graph of the modulus function can be found from the graph of y = x by reflecting the negative x part of the graph to make the function values positive. This is shown in Figure 2.19.

f02-19-9780750658553
Figure 2.19 The graph of the modulus function y = [x] obtained from the graph of y = x. (a) The graph of y = x with the negative part of the graph displayed as a dotted line. This is reflected about the x-axis to give y = −x for x < 0. (b) The graph of y = [x].

2.8 Symmetry of functions and their graphs

Functions can be classified as even, odd, or neither of these.

Even functions

Even functions are those that can be reflected in the y-axis and then result in the same graph. Examples of even functions are (see Figure 2.20):

y=x3,???y=∣∣x∣∣,???y=x4.

si28_e

f02-20-9780750658553
Figure 2.20 y= x2, y = [x], and y = x4 are even functions

As previously discussed, reflecting in the y-axis results from replacing x by −x in the function expression and hence the condition for a function to be even is that substituting −x for x does not change the function expression, that is, f(x) = f (− x).

Example 2.6

Show that 3x2 − x4 is an even function. Substitute −x for x in the expression f(x) = 3x2 − x4 and we get

f(−x)=3(−x)2−(−x)4=3(−1)2(x)2−(−1)4(x)4=3x2−x4.

si29_e

So, we have found that f (− x) = f(x) and therefore the function is even.

Odd functions

Odd functions are those that when reflected in the y-axis result in an upside down version of the same graph. Examples of odd functions are (see Figure 2.21):

y=x,???y=x3,???y=1x

si30_e

f02-21-9780750658553
Figure 2.21 (a) y = x, (b) y = x3, (c) y = 1/x are odd functions. If they are reflected in the y-axis they result in an upside down version of the original graph.

Reflecting in the y-axis results from replacing x by −x in the function expression and the upside down version of the function f(x) is found by multiplying the function by −1. Hence, the condition for a function to be odd is that substituting −x for x gives − f(x), that is,

f(−x)=−f(x).

si31_e

Example 2.7

Show that 4x–(1/x) is an odd function. Substitute x for –x in the expression f(x) = 4x – (1/x) and we get

f(−x)=4(−x)−1−x=−4x+1x=−(4x−1x).

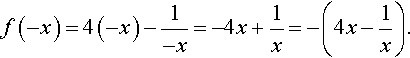
si32_e

We have found that f(−x) = −f(x), so the function is odd.

2.9 Solving inequalities

For linear and quadratic functions, y = f(x), we have discussed how to find the values where the graph of the functions crosses the x-axis, that is how to solve the equation f(x) = 0. It is often of interest to find ranges of values of x where f(x) is negative or where f(x) is positive. This means solving inequalities like f(x) < 0 or f(x) > 0, respectively.

Like equations, inequalities can be solved by looking for equivalent inequalities. One way of finding these is by doing the same thing to both sides of the expression. There is an important exception for inequalities that if both sides are multiplied or divided by a negative number then the direction of the inequality must be reversed.

To demonstrate these equivalences begin with a true proposition

3<5??or‘3?is?less?than?5’

si33_e

Add 2 on to both sides and it is still true

3+2<5+2,????i.e.5<7.

si34_e

Subtract 10 from both sides and we get

5−10<7−10,????i.e.−5<−3

si35_e

which is also true.

Multiply both sides by −1 and if we do not reverse the inequality we get

(−1)(−5)<(−1)(−3),????i.e.5<3

si36_e

which is false. However, if we use the correct rule that when multiplying by a negative number we must reverse the inequality sign then we get:

(−1)(−5)>(−1)(−3),????i.e.5>3

si37_e

which is true. This process is pictured in Figure 2.22.

f02-22-9780750658553
Figure 2.22 On the number line, numbers to the left are less than numbers to their right: −5 < −3. If the inequality is multiplied by −1 we need to reverse the sign to get 5 > 3.

Note that inequalities can be read from right to left as well as from left to right: 3 < 5 can be read as ‘3 is less than 5’ or as ‘5 is greater than 3’ and so it can also be written the other way round as 5 > 3.

Using a number line to represent inequalities

An inequality can be expressed using a number line as in Figure 2.23. In Figure 2.23(a), the open circle indicates that 3 is not included in the set of values, t < 3. In Figure 2.23(b), the closed circle indicates that −2 is included in the set of values, x ≥ −2. In Figure 2.23(c), the closed circle indicates that the value 4.5 is included in the set y ≤ 4.5.

f02-23-9780750658553
Figure 2.23 Representing inequalities on a number line.

Example 2.8

Find a range of values for t, x, and y such that the following inequalities hold

(a) 2t + 3 < t − 6

(b) x + 5 ≥ 4x − 10

(c) 16 − y > −5y

Solution

(a) 2t + 3 < t − 6 ⇔2t − t + 3 < −6 (subtract t from both sides)
⇔ t < −6–3 (subtract 3 from both sides)
⇔ t < −9.

This solution can be represented on a number line as in Figure 2.24.

f02-24-9780750658553
Figure 2.24 The solution to 2t + 3 < t − 6 is given by t < −9.

(b) x+5 ≥ 4x−10
⇔+5≥ 3x − 10 (subtract x from both sides)
⇔15≥ 3x (add 10 to both sides)
⇔5≥ x (divide both sides by 3)
⇔x ≤5.

This solution in represented in Figure 2.25.

f02-25-9780750658553
Figure 2.25 The solution to x + 5 ≥ 4x − 10 is found to be x ≤ 5, here represented on a number line.

(c) 16 − y > −5y
⇔ 16 > −4y (add y to both sides)
⇔ −4 < y (divide by − 4 and reverse the sign)
⇔ y > −4.

This solution is represented in Figure 2.26.

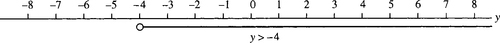
f02-26-9780750658553
Figure 2.26 The solution to 16 − y > −5 y is found to be y > −4, here pictured on a number line.

Representing compound inequalities on a number line

We sometimes need a picture of the range of values given if two inequalities hold simultaneously, for instance x ≥ 3 and x < 5. This is analysed in Figure 2.27(a) and we can see that for both inequalities to hold simultaneously x must lie in the overlapping region where 3 ≤ x < 5. 3 ≤ x < 5 is a way of expressing that x lies between 3 and 5 or is equal to 3. In the example in Figure 2.27(b), x > 6 and x > 2, and for them both to hold then x > 6.

f02-27-9780750658553
Figure 2.27 (a) x ≥ 3 and x < 5. (b) x > 6 and x > 2 combines to give x > 6. (c) x < 5 or x ≥ 7. (d) x < 2 or x ≥ 0.

Another possible way of combining inequalities is to say that one or another inequality holds. Examples of this are given in Figure 2.27(c) where x < 5 or x ≥ 7 and this gives the set of values less than 5 or greater than or equal to 7. Figure 2.27(d) gives the example where x < 2 or x ≥ 0 and in this case it results in all numbers lying on the number line, that is, x ∈ r.

Example 2.9

Find solutions to the following combinations of inequal- ities and represent them on a number line.

(a) x + 3 > 4 and x−1 < 5,

(b) 1−u<3u+2 or μ+2≥6,

(c) t + 5 > 12 and −t > 24.

Solution

(a) x + 3 > 4 and x−1 < 5 We solve both inequalities separately and then combine their solution sets

x+3>4???⇔???x>1??(subtracting?3?from?both?sides)x−1<5???⇔???x<6(adding?1?to?both?sides)

si38_e

So the combined inequality giving the solution is x > 1 and x < 6. which from Figure 2.28(a) we can see is the same as 1 < x < 6.

f02-28-9780750658553
Figure 2.28 Solutions to compound inequalities as given in Example 2.8 represented on a number line.

(b) 1 − u < 3u + 2 or u + 2 ≥6
We solve both inequalities separately and then combine their solution sets,

1−u<3u+2⇔−1<4u(subtracting?2?from?both?sides)⇔−14<u(dividing?both?sides?by?4)

si39_e



⇔???u>−14u+2≥6⇔????u≥4((subtracting?2?from?both?sides)

si40_e



Combining the two solutions gives u > −1/4 or u ≥ 4 and this is represented on the number line in Figure 2.28(b) where we can see that it is the same as u > −1/4.

(c) 

t+5>12??and??−t>24t+5>12????⇔t>7(subtracting?5?from?both?sides)−t>24????⇔t<−24(multiply?both?sides?by−1?and?reverse?the?inequality?sign))

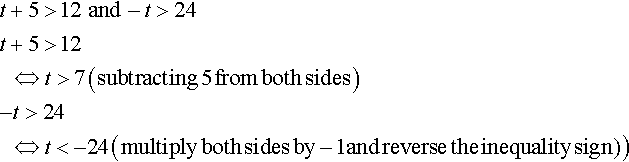
si41_e


Combining the two solutions sets gives t > 7 and t < − 24 and we can see from Figure 2.28(c) that this is impossible and hence there are no solutions.

Solving more difficult inequalities

To solve more difficult inequalities, our ideas about equivalence are not enough on their own, we also use our knowledge about continuous functions. In the previous chapter, we defined a continuous function as one that could be drawn without taking the pen off the paper. If we wish to solve the inequality f(x) > 0 and we know that f(x) is continuous then we can picture the problem graphically as in Figure 2.29. From the graph we can see that to solve the inequality we need only find the values where f(x) = 0 (the roots of f(x) = 0) and determine whether f(x) is positive or negative between the values of x where f(x) = 0. To do this, we can use any value of x between the roots. We are using the fact that as f(x) is continuous then it can only change from positive to negative by going through zero.

f02-29-9780750658553
Figure 2.29 The graph of a continuous function. To solve for f(x) > 0, we first find the values where f(x) = 0. On the graph these are marked as a, b, c, and d. If the function is above the x-axis then the function values are positive, if the function lies below the x-axis then the function values are negative. The solution to f(x) > 0 is given by those values of x for which the function lies above the x-axis, that is, y positive. For the function represented in the graph the solution to f(x) > 0 is x < a or b < x < C or x > d

Example 2.10

Find the values of t such that t2 − 3t < − 2. Write the inequality with 0 on one side of the inequality sign

t2−3t<−2⇔t2−3t+2<0(adding?2?to?both?sides)

si42_e

Find the solutions to f(t) = t2 − 3t + 2 = 0 and mark them on a number line as in Figure 2.30.

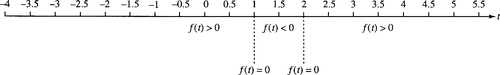
f02-30-9780750658553
Figure 2.30 Solving t2− 3t + 2 < 0 (Example 2.10).

Using the formula

t=−b±b2−4ac√2a

si43_e

where a = 1, b = −3, and c = 2 gives

t=−3±9−8√2??????⇔t=3±12??????⇔t=3±12???or???t=3−12??????⇔t=2??????or????t=1

si44_e

Substitute values for t which lie on either side of the roots of f(t) in order to find the sign of the function between the roots. Here we choose 0, 1.5, and 3.

When t = 0

t2−3t+2=(0)2−3(0)+2=0+0+2=2

si45_e

which is positive, giving f(t) > 0. When t = 1.5

t2−3t+2=(1.5)2−3(1.5)+2=2.25−4.5+2=−0.25

si46_e

which is negative giving f(t) < 0. When t = 3

t2−3t+2=(3)2−3(3)+2=9−9+2=2

si47_e

which is positive, giving f(t) > 0.

By marking the regions on the number line, given in Figure 2.30, with f(t) > 0, f(t) < 0, or f(t) = 0 as appropriate we can now find the solution to our inequality f(t) < 0 which is given by the region where 1 < t < 2.

Example 2.11

Find the values of x such that (x2 − 4)(x + 1) > 0.

Solution The inequality already has 0 on one side of the inequality sign so we begin by finding the roots to f(x) = 0, that is,

(x2−4)(x+1)>0

si48_e

Factorization gives

(x2−4)(x+1)>0⇔(x−2)(x+2)(x+1)=0

si49_e

⇔ x = 2, x = −2, or x = −1. So the roots are −2, −1, and 2. These roots are pictured on the number line in Figure 2.31.

f02-31-9780750658553
Figure 2.31 Solving (x2− 4) (x + 1) > 0 (Example 2.11).

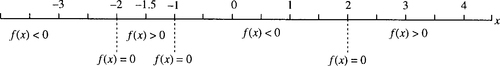
Substitute values for x which lie on either side of the roots of f(x) in order to find the sign of the function between the roots. Here we choose −3, −1.5, 0, and 2.5.

When x = −3

(x−2)(x+2)(x+1)===0?gives(−3−2)(−3+2)(−3+1)(−5)(−1)(−2)−10,??giving?f(x)<0.

si50_e

When x = 1.5

(x−2)(x+2)(x+1)???gives??(−1.5−2)(−1.5+2)(−1.5+1)=(−3.5)(0.5)(−0.5)=0.875,????givingf(x)>0.

si51_e

When x = 0

(x−2)(x+2)(x+1)???gives??(0−2)(0+2)(0+1)=(−2)(2)(1)=−4,????giving?f(x)<0.

si52_e

When x = 2.5

(x−2)(x+2)(x+1)???gives??(2.5−2)(2.5+2)(2.5+1)=(0.5)(4.5)(3.5)=7.875,????giving?f(x)>0.

si53_e

These regions are marked on the number line as in Figure 2.31 and the solution is given by those regions where f(x) > 0 Looking for the regions where f(x) > 0 gives the solution as − 2 < x < −1 or x > 2.

2.10 Using graphs to find an expression for the function from experimental data

Linear relationships

Linear relationships are the easiest ones to determine from experimental data. The points are plotted on a graph and if they appear to follow a straight line then a line can be drawn by hand and the equation can be found using the method given in Section 2.2.

Example 2.12

A spring is stretched by hanging various weights on it and in each case the length of the spring is measured.

Mass (kg)0.1250.250.5123
Length (m)0.40.410.4350.50.620.74

cetable1a

Approximate the length of the spring when no weight is hung from it and find the expression for the length in terms of the mass.

Solution First, draw a graph of the given experimental data. This is done in Figure 2.32.

f02-32-9780750658553
Figure 2.32 The data for length of spring against mass of the weight as given in the Example 2.11. The line is a fitted by eye to the experimental data and the equation of the line can be found using the method of Section 2.2.

A line is fitted by eye to the data. The data does not lie exactly on a line due to experimental error and due to slight distortion of the spring with heavier weights. From the line we have drawn we can find the gradient by choosing any two points on the line and calculating

change?in?ychange?in?x.

si54_e

Taking the two points as (0,0.28) and (2,0.58), we get the gradient as

0.58−0.382−0=0.22=0.1.

si55_e

The point where it crosses the y-axis, that is, where the mass hung on the spring is 0 can be found by extending the line until it crosses the y-axis. This gives 0.38 m.

Finally, the expression for the length in terms of the mass of the attached weight is given by y = mx + c, where y is the length and x is the mass,

m is the gradient and c is the value of y when x = 0, that is, where there is no weight on the string. This gives

length = 0.1 × mass + 0.38

The initial length of the spring is 0.38 m.

Exponential relationships

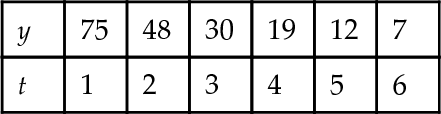
Many practical relationships behave exponentially particularly those involving growth or decay. Here it is slightly less easy to find the relationship from the experimental data, however, it is simplified by using a log–linear plot. Instead of plotting the values of the dependent variable, y, we plot the values of log10(y). If the relationship between y and time, t, is exponential as we suspected then the log10(y) against t plot will be a straight line.

The reason this works can be explained as follows. Supposing y = y0 10kt where y0 is the value of y when t = 0 and k is some constant; then, taking the log base 10 of both sides, we get

log10(y)==log10(y010kt)log10(y0)+log10(10kt).

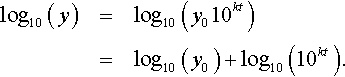
si56_e

As the logarithm base 10 and raising to the power of 10 are inverse operations, we get

log10(y)=log10(y0)+kt

si57_e

As y0 is a constant, the initial value of y, and k is a constant then we can see that this expression shows that we shall get a straight line if log10 (y) is plotted against t. The constant k is given by the gradient of the line and log10(y0) is the value of log10(y) where it crosses the vertical axis. Setting Y = log10(y), c = log10(y0)

Y=c+kt

si58_e

which is the equation of the straight line.

Example 2.13

A room was tested for its acoustical absorption properties by playing a single note on a trombone. Once the sound had reached its maximum intensity, the player stopped and the sound intensity was measured for the next 0.2 s at regular intervals of 0.02 s. The initial maximum intensity at time 0 is 1.0. The readings were as follows:

Time(s)00.020.040.060.080.10.120.140.160.180.2
Intensity1.00.630.350.220.130.080.050.030.020.010.005

cetable13a

Draw a graph of intensity against time and log (intensity) against time and use the latter plot to approximate the relationship between the intensity and time.

Solution The graphs are plotted in Figure 2.33 where, for the second graph (b), we take the log10 (intensity) and use the table below:

f02-33-9780750658553
Figure 2.33 (a) Graph of sound intensity against time as given in Example 2.13. (b) Graph of log10 (intensity) against time and a line fitted by eye to the data. The line goes through the points (0,0) and (0.2, −2.2).
Time0 0.020.040.060.080.10.120.140.160.180.2
log10 (intensity)0–0.22–0.46–0.66–0.89–1.1–1.3–1.5–1.7–2–2.3

cetable1

We can see that the second graph is approximately a straight line and therefore we can assume that the relationship between the intensity and time is exponential and could be expressed as I = I010kt. The log10 of this gives

log10(I)=log10(I0)+kt.

si59_e

From the graph in Figure 2.33(b), we can measure the gradient, k. To do this we calculate

change?in?log10(intensity)change?in?time

si60_e

giving

−2.2−00.2−0=−11=k.

si61_e

The point at which it crosses the vertical axis gives

log10(I0)=0⇔I0=100=1.

si62_e

Therefore, the expression I = I0 10kt becomes

I=10−11t.

si63_e

Power relationships

Another common type of relationship between quantities is when there is a power of the independent variable involved. In this case, if y = axn where n could be positive or negative then the value of a and n can be found by drawing a log–log plot.

This is because taking log10 of both sides of y = axn gives

log10(y)=log10(axn)=log10(a)+n?log10(x)

si64_e

Replacing Y = log10(y) and X = log10(x) we get:

Y=log10(a)+nX,

si65_e

showing that the log–log plot will give a straight line, where the slope of the line will give the power of x and the position where the line crosses the vertical axis will give the log10(a). Having found a and n, they can be substituted back into the expression

y=axn.

si66_e

Example 2.14

The power received from a beacon antenna is though to depend on the inverse square of the distance from the antenna and the receiver. Various measurements, given below, were taken of the power received against distance r from the antenna. Could these be used to justify the inverse square law? If so, what is the constant, A, in the expression:

p=Ar2

si67_e

Power received (W)0.390.10.050.0250.0150.01
Distance from antenna (km)123456

cetable1c

Solution To test whether the relationship is indeed a power relationship we draw a log−log plot. The table of values is found below:

log10 (power)−0.41−1−1.3−1.6−1.8−2
log10 (distance)00.30.50.60.70.78

cetable2

Graphs of power against distance and log10(power) against log10(distance) are given in Figure 2.34(a) and (b).

f02-34-9780750658553
Figure 2.34 (a) Plot of power against distance (Example 2.14). (b) log10 (power) against log10 (distance). In (b), the line is fitted by eye to the data, from which the slope of the graph indicates n in the relationship P = Atn. Two points lying on the line are (0, −0.38) and (0.7, −1.8).

As the second graph is a straight line, we can assume that the relationship is of the form P = Arn where P is the power and r is the distance, In which case, the log–log graph is

log10(P)=log10(A)+n?log10(r).

si68_e

We can measure the slope by calculating

change?in?log10(P)change?in?log10(r)

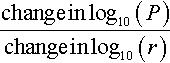
si69_e

and, using the two points that have been found to lie on the line, this gives

−1.8−(−0.38)0.7−0=−2.03.

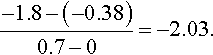
si70_e

As this is very near to − 2, the inverse square law would appear to be justified.

The value of log10(A) is given from where the graph crosses the vertical axis and this gives

log10(A)=−0.38???⇔???A=10−0.38???⇔???A=0.42.

si71_e

So the relationship between power received and distance is approximately

P=0.42r−2=0.42r2.

si72_e

2.11 Summary

1. The linear function y = mx + c has gradient (slope) m and crosses the y-axis at y = c.

2. The gradient, m, of a straight line y = mx + c is given by:

m=change?in?ychange?in?x

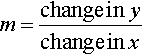
si73_e


and this is the same along the length of the line.

3. The equation of a line which goes through two points, (x1, y1) and (x2, y2) is:

y−y1y2−y1=x−x1x2−x1??????where?y2≠y1.

si74_e


4. The graph of the quadratic function y = ax2 + bx + c is called a parabola. The graph crosses the y-axis (when x = 0) at y = c.

5. There are three possibilities for the roots of the quadratic equation a x2+ bx + c = 0

Case I: two real roots when b2 − 4ac > 0,

Case II: only one unique root when b2 − 4ac = 0,

Case III: no real roots when b2 − 4ac < 0.

6. By considering the graphs of known functions y = f(x), for instance, those given in Figure 2.10, and the following transfor-mations, many other graphs can be drawn.

(a) Replacing x by x + a in the function y = f(x) results in shifting the graph a units to the left.

(b) Replacing f(x) by f(x) + A results in shifting the graph A units upwards.

(c) Replacing x by −x reflects the graph in the y-axis.

(d) Replacing f(x) by − f(x) reflects the graph in the x-axis (turning it upside down).

(e) Replacing x by ax squashes the graph horizontally if a > 1 or stretches it horizontally if 0 < a < 1.

(f) Replacing f(x) by Af(x) stretches the graph vertically if A > 1 or squashes it vertically if 0 < A < 1.

(g) Reflecting the graph of y = f(x) in the line y = x results in the graph of the inverse relation.

7. A function may be even, or odd, or neither of these.

(a) An even function is one whose graph remains the same if reflected inthe y-axis, that is, when x arrow −x. This can also be expressed by the condition

f(−x)=f(x)

si75_e



Examples of even functions are y = x2, y = |x|, and y = x4.

(b) An odd function is one which when reflected in the y-axis, that is, when x arrow −x, gives an upside down version of the original graph (i.e. − f(x)). This can also be expressed as the condition:

f(−x)=−f(x)

si76_e



Examples of odd functions are y = x and y = x3.

8. Not all functions have true inverses. Only one-to-one functions have inverse functions. A function is one-to-one if any line y = constant drawn on the graph y = f(x) crosses the function only once. This means there is exactly one value of x that gives each value of y.

9. Simple inequalities can be solved by finding equivalent inequalities. Inequalities remain equivalent if both sides of the inequality have the same expression added or subtracted. They may also be multiplied or divided by a positive number but if they are multiplied or divided by a negative number then the direction of the inequality sign must be reversed.

10. To solve the inequalities f(x) > 0, f(x) < 0, f(x) ≤ 0, or f(x) ≥ 0, where f(x) is a continuous function, solve f(x) = 0 and choose any value for x around the roots to find the sign of f(x) for each region of values for x.

11. Graphs can be used to find relationships in experimental data. First, plot the data then:

(a) If the data lies on an approximate straight line then draw a straight line through the data and find the equation of the line.

(b) If it looks exponential, then take the log of the values of the dependent variable and draw a log–linear graph. If this looks approximately like a straight line then assume there is an exponential relationship y = y0 10kt, where k is given by the gradient of the line and log10(y0) is the value where the graph crosses the vertical axis.

(c) If the relationship looks something like a power relationship, y = Axn, then take the log of both sets of data and draw a log–log graph. If this is approximately like a straight line, then assume there is a power relationship and n is given by the gradient of the line and log10A is the value where the graph crosses the vertical axis.

2.12 Exercises

2.1. Sketch the graphs of the following:

(a)y=3x−1,(c)y=−5x,(b)y=2x+1,(d)y=12x−3.

si77_e


In each case state the gradient of the line.

2.2. A straight line passes through the pair of points given. Find the gradient of the line in each case.

(a)(0,1),(1,4)(c)(−1,−1),(6,3)(b)(1,1),(2,−4)(d)(1,4),(3,4)

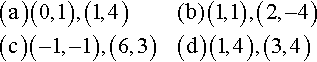
si78_e


2.3. A straight line graph has gradient −5 and passes through (1,6). Find the equation of the line.

2.4. In Figure 2.35 are various graphs drawn to the scale 1 unit = 1 cm. By finding the gradients of the lines and where they cross the y-axis, find the equation of the line.

f02-35-9780750658553
Figure 2.35 Straight line graphs for Exercise 2.4.

2.5. A straight line passes through the pair of points given. Find the equation of the line in each case.

(a)(0,1),(−1,4)(c)(1,1),(6,3)(b)(1,1),(−2,−4)(d)(−1,−4),(−3,−4)

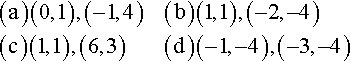
si79_e


2.6. Find the values of x such that f (x) = 0 for the following functions

(a) f(x) = x2 − 4,

(b) f(x) = (2x − 1)(x + 1),

(c) f(x) = (x − 3)2,

(d) f(x) = (x − 4)(x + 4),

(e) f(x) = x2 + x − 6,

(f) f(x) = x2 + 7 x + 12,

(g) f(x) = 12 x2 − 12 x − 144.
Using the fact that the peak or trough in the parabola, y = f(x), occurs at a value of x half-way between the values where f(x) = 0 then sketch graphs of the above quadratic functions.

2.7. By considering transformations of simple functions sketch graphs of the following:

(a)?y=1x−(1/2),(c)?y=12x3,(e)?y=(2x−1)2(g)?y=log2(x+2),(i)?y=4x−x2.(b)?y=3.2−x,(d)?y=−3(1/2)x,(f)?y=(2x−1)2−2,(h)?y=6−2x,

si80_e


2.8. Consider reflections of the graphs given in Figure 2.36 to determine whether they are even, odd, or neither of these.

f02-36-9780750658553
Figure 2.36 Graphs of functions for Exercise 2.7.

2.9. By substituting x arrow −x in the following functions determine whether they are odd, even, or neither of these:

(a)?y=−x2+1x2??wheree?x≠0,(b)?y=∣∣x3∣∣−x2,(c)?y=−1x+log2(x)??where?x>?0,(d)?y=−1x+x+x5(e)?y=6+x2(f)?y=1−|x|.

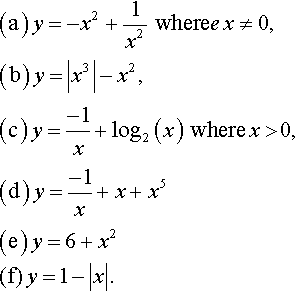
si81_e


2.10. Draw graphs of the following functions and draw the graph of the inverse relation in each case. Is the inverse a function?

(a)?f(t)=−t+2,(c)?h(w)=4w+2.(b)?g(x)=(x−2)2,

si82_e


2.11. Find the range of values for which the following inequalities hold and represent them on a number line.

(a) 10t − 2 ≤ 31,

(b) 10x − 3x > −2,

(c) 3–4 y ≥ 11 + y,

(d) t + 15 < 6 − 2t.

2.12. Find the range of values for which the following hold and represent them on a number line:

(a) x − 2 > 4 or 1 − x < 12,

(b) 4t + 2 ≥ 10 and 3 − 2t < 1,

(c) 3 u + 10 > 16 or 3 − 2u > 13.

2.13. Solve the following inequalities and represent the solutions on a number line:

(a) x2 − 4 < 5,

(b) (2x − 3) (x + 1) (x − 5) > 0,

(c) t2 + 4t ≤ 21,

(d) 4w2+ 4w − 35 ≥ 0.

2.14. For the following sets of data, y is thought to depend exponentially on t. Draw log–linear graphs in each case and find constants A and k such that y = A10kt.

(a) 

y75483019127
t123456

cetable10a


(b) 

y24.28.5183573
t0.10.20.30.40.50.6

cetable5a


2.15. An experiment measuring the change in volume of a gas as the pressure is decreased gave the following measurements:

P (105 N m −2)1.51.41.31.21.11
V (m3)0.9511.051.11.161.24

cetable1aa



If the gas is assumed to be ideal and the expansion is adiabatic then the relationship between pressure and volume should be:

pVy=C

si83_e


where y and C are constants and p is the pressure and V is the volume. Find reasonable values of y and C to fit the data and from this expression find the predicted volume at atmospheric pressure, p = 1.013 × 105 N m−2.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
18.116.201.23