15.8 Solving linear difference equations with constant coefficients using z transforms

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Using partial fractions to find the inverse transform

Example 15.29

Find

$Z^{- 1} {\frac{z^{2}}{(z - 1) (z - 0.5)}} .$

si231_e

Solution Notice that most of the values of the transform in Table 15.2 have a factor of z in the numerator. We write

$\frac{z^{2}}{(z - 1) (z - 0.5)} = z (\frac{z}{(z - 1) (z - 0.5)})$

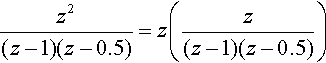
si232_e

We use the 'cover up’ rule to write

$\begin{matrix} \frac{z}{(z - 1) (z - 0.5)} = \frac{1}{0.5 (z - 1)} - \frac{1}{z - 0.5} \\ = \frac{2}{z - 1} - \frac{1}{z - 0.5} \end{matrix}$

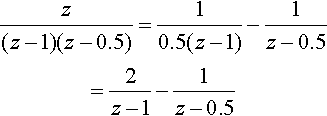
si233_e

$\frac{z^{2}}{(z - 1) (z - 0.5)} = \frac{2 z}{z - 1} - \frac{z}{z - 0.5}$

si234_e

and using Table 15.2 we find

$Z^{- 1} {\frac{2 z}{z - 1} - \frac{z}{z - 0.5}} = 2 u_{n} - {(0.5)}^{n}$

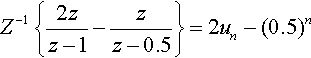
si235_e

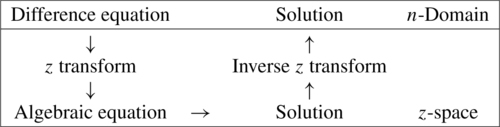
15.8 Solving linear difference equations with constant coefficients using z transforms

The scheme for solving difference equations is very similar to that for solving differential equations using Laplace transforms and is outlined below. The z transform transforms the linear difference equation with constant coefficients to an algebraic equation in z. This can be solved and then the inverse transform of this solution gives the solution to the original difference equation.

Example 15.30

Solve the difference equation

$y_{n} + 2 y_{n - 1} = 2 u_{n}$

for n ≥ 0 given y₋₁ = 1.

Solution We take the z transform of both sides of the difference equation

$y_{n} + 2 y_{n - 1} = 2 u_{n}$

and using the right shift property to find

$Z {y_{n - 1}} = z^{- 1} Y (z) + y_{- 1}$

we get

$Y (z) + 2 (z^{- 1} ? Y (z) + y^{- 1}) = \frac{2 z}{z - 1} .$

si239_e

As $y_{- 1} = 1$ ,

$\begin{matrix} Y (z) (1 + 2 z^{- 1}) = \frac{2 z}{z - 1} - 2 \\ Y (z) = \frac{2 z^{2}}{(z - 1) (z + 2)} - \frac{2 z}{(z + 2)} . \end{matrix}$

si241_e

To take the inverse transform we need to express the first terms using partial fractions. Using the ‘cover up’ rule we get

$\frac{2 z}{(z - 1) (z + 2)} = \frac{2}{3 (z - 1)} + \frac{4}{3 (z + 2)}$

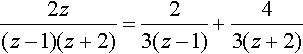
si242_e

$Y (z) = \frac{2 z}{3 (z - 1)} + \frac{4 z}{3 (z + 2)} - \frac{2 z}{(z + 2)} = \frac{2 z}{3 (z - 1)} - \frac{2 z}{3 (z + 2)} .$

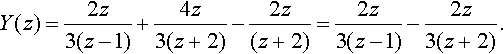
si243_e

Taking inverse transforms we find

$y_{n} = \frac{2}{3} u_{n} - \frac{2}{3} {(- 2)}^{n}$

si244_e

Check: To check that we have the correct solution we can substitute in a couple of values for n and see that we get the same value from the difference equation as from the explicit formula found.

From the explicit formula and using u₀ = 1 (by definition of the unit step function), n = 0 gives

$y_{0} = \frac{2}{3} u_{0} - \frac{2}{3} {(- 2)}^{0} = \frac{2}{3} - \frac{2}{3} = 0$

si245_e

From the difference equation, y_n+ 2y_n−1 = 2u_n’where y₋₁ = 1, n = 0 gives

$y_{0} + 2 y_{- 1} = 2 u_{0} .$

Substituting y₋₁ = 1 gives y₀ = 0 as before.

From the explicit formula, n = 1 gives

$y_{1} = \frac{2}{3} u_{1} - \frac{2}{3} {(- 2)}^{1} = \frac{2}{3} + \frac{4}{3} = 2.$

si247_e

From the difference equation, n = 1gives

$y_{1} + 2 y_{0} = 2 u_{1}$

substituting y₀ = 0 gives y₁ = 2, confirming the result of the explicit formula.

Example 15.31

Solve the difference equation

$6 y_{n} - 5 y_{n -1} + y_{n - 2} = {(0.25)}^{n} ? ? ? ? n \geq 0$

given y₋₁ = 1, y₋₂ = 0.

Solution We take the z transform of both sides of the difference equation 6y_n −5y_n−1 + y_n−2 = (0.25)ⁿ and use the right shift property to find

$\begin{array}{l} Z {y_{n - 1}} = z^{- 1} Y (z) + y_{- 1} \\ Z {y_{n - 2}} = z^{- 2} Y (z) + z^{- 1} y_{- 1} + y_{- 2} \end{array}$

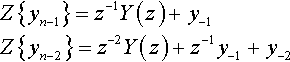
si250_e

which gives

$6 Y (z) - 5 (z^{- 1} Y (z) + y_{- 1}) + z^{- 2} Y (z) + y_{- 2} + z^{- 1} y_{- 1} = \frac{2}{z - 0.25} .$

si251_e

Substituting the initial conditions y₋₁ = 1 and y₋₂ = 0 and collecting the terms involving Y(z) we get

$\begin{array}{l} Y (z) (6 - 5 z^{- 1} Y (z) + z^{- 2}) - 5 + z^{- 1} = \frac{z}{z - 0.25} \\ ? ? ? ? ? \Leftrightarrow Y (z) = \frac{z}{(z - 0.25) (6 - 5 z^{- 1} + z^{- 2})} + \frac{5}{6 - 5 z^{- 1} + z^{- 2}} \\ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? - \frac{z^{- 1}}{6 - 5 z^{- 1} + z^{- 2}} \\ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? = z (\frac{z^{2}}{(z - 0.25) (6 z^{2} - 5 z + 1)}) + z (\frac{5 z}{(3 z - 1) (2 z - 1)}) \\ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? - z (\frac{1}{(3 z - 1) (2 z - 1)}) . \end{array}$

si252_e

Using the ‘cover up’ rule we write each of these terms as partial fractions:

$\begin{array}{l} \frac{z^{2}}{(z - 0.25) (3 z - 1) (2 z - 1)} \\ ? ? ? ? ? ? ? ? = \frac{z^{2}}{6 (z - \frac{1}{4}) (z - \frac{1}{3}) (z - \frac{1}{2})} \\ ? ? ? ? ? ? ? ? = \frac{1}{2 (z - \frac{1}{4})} - \frac{4}{3} \frac{1}{(z - \frac{1}{3})} + \frac{1}{(z - \frac{1}{2})} \\ ? ? ? ? ? ? ? ? \frac{5 z}{6 (z - \frac{1}{3}) (z - \frac{1}{2})} = \frac{- 5}{3 (z - \frac{1}{3})} + \frac{5}{2 (z - \frac{1}{2})} \\ ? ? ? ? ? ? ? ? \frac{1}{3 (z - 1) (2 z - 1)} = \frac{1}{6 (z - \frac{1}{3}) (z - \frac{1}{2})} \\ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? = \frac{- 1}{z - \frac{1}{3}} + \frac{1}{z - \frac{1}{2}} \end{array}$

si253_e

giving

$\begin{array}{l} Y (z) = \frac{z}{2 (z - \frac{1}{4})} - \frac{4 z}{3 (z - \frac{1}{3})} + \frac{z}{z - \frac{1}{2}} - \frac{5 z}{3 (z - \frac{1}{3})} \\ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? + \frac{5 z}{2 (z - \frac{1}{2})} + \frac{z}{z - \frac{1}{3}} - \frac{z}{z - \frac{1}{2}} \\ ? ? ? ? ? ? ? ? ? ? ? \Leftrightarrow Y (z) = \frac{z}{2 (z - \frac{1}{4})} - \frac{2 z}{z - \frac{1}{3}} + \frac{5}{2 (z - \frac{1}{2})} . \end{array}$

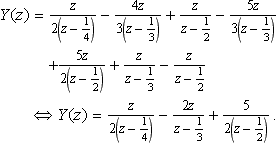
si254_e

Taking the inverse transform:

$y_{n} = \frac{1}{2} {(\frac{1}{4})}^{n} - 2 {(\frac{1}{3})}^{n} + \frac{5}{2} {(\frac{1}{2})}^{n}$

si255_e

15.9 z transforms and systems theory

The transfer function and impulse response function

As before, when considering Laplace transforms, we find that an important role is played by the impulse response function in systems theory of discrete systems. If this case is a sequence, h_n, its z transform of is called the transfer function (or system function). We remember from Chapter 14 that a linear, time-invariant system is represented by a linear difference equation with constant coefficients, that is, a second-order LTI system can be represented by

$a y_{n} + b y_{n - 1} + c y_{n - 2} = f_{n} .$

If we take f_n as the delta function δ_n, we get

$a y_{n} + b y_{n - 1} + c y_{n - 2} = δ_{n} .$

By definition of the impulse response function we consider all initial conditions to be 0, that is, y₋₁ = 0, y₋₂ = 0; taking the z transform we get

$\begin{array}{l} a Y (z) + b z^{- 1} Y (z) + c z^{- 2} Y (z) = 1 \\ Y (z) (a + b z^{- 1} + c z^{- 2}) = 1 \\ Y (z) = \frac{1}{a + b z^{- 1} + c z^{- 2}} \\ Y (z) = \frac{z^{2}}{a z^{2} + b z + c} . \end{array}$

si258_e

Notice that the poles of this function are found by solving az²+bz+c = 0, which we recognize as the auxiliary equation or characteristic equation from Chapter 14.

This function, the z transform of the impulse response function, is called the transfer function and is usually denoted by H(z), so we have

$H (z) = z^{2} / (a z^{2} + b z + c)$

and Z⁻¹{H(z)}= h_n, where h_nis the impulse response function.

Example 15.32

Find the transfer function and impulse response of the system described by the following difference equation:

$3 y_{n} + 4 y_{n - 1} = f_{n}$

Solution To find the transfer function replace f_n by δ_nand take the z transform of the resulting equation assuming zero initial conditions:

$4 y_{n} + 3 y_{n - 1} = δ_{n} .$

Taking the z transform of both sides of the equation we get

$\begin{array}{l} 4 Y + 3 (z^{- 1} Y + y_{- 1}) = 1. \\ As ? y_{- 1} = 0, \\ Y = \frac{z}{4 z + 3} = H (z) = \frac{z / 4}{z + (3 / 4)} . \end{array}$

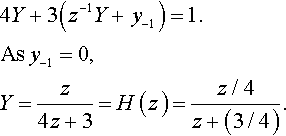
si262_e

To find the impulse response sequence we take the inverse transform of the transfer function to find

$h_{n} = Z^{- 1} {\frac{z / 4}{z + \frac{3}{4}}} = \frac{1}{4} {(- \frac{3}{4})}^{n}$

si263_e

We can now see why, in the design of digital filters, this is referred to as an infinite impulse response (IIR) filter. This impulse response has a non-zero value for all n. Hence it represents an IIR system.

We now discover that we can find the system response to any input sequence f_n, with zero initial conditions, by using the transfer function.

Response of a system with zero initial conditions to any input f_n

Assuming all initial conditions are zero, that is, y₋₁ = 0 and y₋₂ = 0, then the equation

$a y_{n} + b y_{n - 1} + c y_{n - 2} = f_{n}$

transforms to become

$a Y (z) + b z^{- 1} Y (z) + c z^{- 2} Y (z) = F (z) \Leftrightarrow y (z) = \frac{F (z) z^{2}}{a z^{2} + b z + c} .$

si265_e

We have just discovered that the transfer function, H(z) is given by

$H (z) = \frac{z^{2}}{a z^{2} + b z + c} .$

si266_e

Then we find that

$Y (z) = F (z) H (z) .$

In order to find the response of the system to the function f_n we take the inverse transform of this expression. We are able to use the convolution property of z transforms, which states:

$Z {\sum_{k = 0}^{n} f_{k} g_{n - k}} = F (z) G (z)$

si268_e

or equivalently

$Z^{- 1} {F (z) G (z)} = \sum_{k = 0}^{n} f_{k} g_{n - k} .$

si269_e

So we find that the response of the system with zero initial conditions to any input sequence f_n is given by the convolution of f_n with the system's impulse response:

$y_{n} = Z^{- 1} {F (z) H (z)} = f_{n} * h_{n},$

We can use this result to solve two types of problems, given zero initial conditions. If we know the impulse response function of the system then we can find the system response to any input f_n either by convolving the two sequences

$y_{n} = \sum_{k = 0}^{n} f_{k} h_{n - k} = f_{n} * h_{n}$

si271_e

or by finding the z transform of fn, F(z) finding the transfer function of the system Z{h_n} = H(z), then finding Y(z) = H(z)F(z) and taking the inverse transform of this to find y_n. This type of problem is called a convolution problem. The other type of problem is that given any output, y_n, and given the input, f_n we can deduce the impulse response of the system. This we do by finding F(z)= Z{l_n}, Y(z) = Z{Y_n} and then H(z)= Y(z)/F(z), thus giving the transfer function. To find the impulse response we find h_n = Z^−l {H(z)}.

Example 15.33

The impulse response of a system is known to be h_n = 3(0.5)ⁿ. Find the response of the system to an input of f(t) = 2u_n given zero initial conditions.

Solution Method 1. We can take z transforms and use

$Y (z) = H (z) F (z)$

In this case

$\begin{array}{l} h_{n} = 3 {(0.5)}^{n} \Leftrightarrow H (z) = Z {3 {(0.5)}^{n}} = \frac{3 z}{z - 0.5} \\ f (t) = 2 u_{n} \Leftrightarrow F (z) = Z {2 u_{n}} = \frac{2 z}{z - 1} \end{array}$

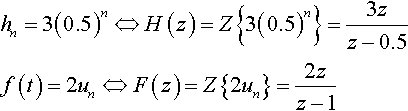
si273_e

Hence,

$Y (z) = H (z) F (z) = \frac{6 z^{2}}{(z - 0.5) (z - 1)} .$

si274_e

As we want to find y_n, we use partial fractions

$\frac{6 z}{(z - 0.5) (z - 1)} = \frac{- 6}{z - 0.5} + \frac{12}{z - 1}$

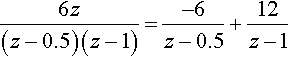
si275_e

(using the 'cover up’ rule). We can know take the inverse transform to find the system response

$\begin{array}{l} y_{n} = Z^{- 1} {Y (z)} = Z^{- 1} {\frac{- 6 z}{z - 0.5} + \frac{12 z}{z - 1}} \\ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? = - 6 {(0.5)}^{n} + 12 u_{n} . \end{array}$

si276_e

Alternative method. Find y_nby taking the convolution of f_n with the impulse response function

$y_{n} = f_{n} * h_{n} = (2 u_{n}) * (3 {(0.5)}^{n}) .$

By definition of convolution

$y_{n} = \sum_{k = 0}^{n} 2 u_{k} (3 {(0.5)}^{n - k}) = \sum_{k = 0}^{n} 6 {(0.5)}^{n - k} .$

si278_e

Writing out some of these terms we get

$\begin{array}{l} ? ? ? ? ? 6, & 6 (0.5 + 1), & 6 ({(0.5)}^{2} + 0.5 + 1), \\ (n = 0) & ? ? ? ? ? (n = 1) & ? ? ? ? ? ? ? ? ? ? ? ? (n = 2) \end{array}$

si279_e

$\begin{matrix} 6 ({(0.5)}^{3} + {0.5}^{2} + 0.5 + 1) . \\ (n = 3) \end{matrix}$

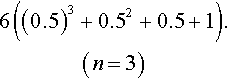
si280_e

We see that each term in the sequence is a geometric progression with first term 6 and common ratio 0.5 and n + 1 terms. Hence

$\begin{array}{l} y_{n} = \frac{6 {(1 - 0.5)}^{n + 1}}{1 - 0.5} = 12 (1 - {(0.5)}^{n + 1}) = 12 - 12 (0.5) {(0.5)}^{n} \\ ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? = 12 - 6 {(0.5)}^{n} \end{array}$

si281_e

which confirms the result of the first method.

The frequency response

As in the case of Laplace transforms and continuous systems, we find we are able to establish a relationship between the transfer function and the steady state response to a single frequency input.

The steady state response of the system to a sequence representing a single frequency input, e^jωn, is found to be

$Y (z) = H (e^{j ω}) e^{j ω n} .$

We can then see that for a single sinusoidal input the steady state response is found by substituting z = e^j^ω into the transfer function for the system and multiplying the resulting complex constant by the sinusoidal input. In other words, the steady state response is a scaled and phase shifted version of the input. The function H (e^j^ω) is called the frequency response function for a discrete system.

Example 15.34

A system transfer function is known to be

$H (z) = \frac{z}{z + 0.2} .$

Find the steady state response to the following:

(a)

$f_{n} = e^{j 2 n};$

(b)

$f (t) = cos (2 n) .$

Solution (a) The steady state response to a single frequency e^j^ωⁿ is given by H (e^j^ω)e^j^ωn. f_n= e^j2ⁿ, so in this case ω = 2 and H (z) is given as z/ (z + 0.2). Hence, we get the steady state response as

$\frac{e^{j^{2}}}{e^{j^{2}} + 0.2} e^{j^{2 n}} .$

si286_e

(b) Using $\frac{1}{2} H (e^{j ω}) e^{j ω t} + H (e^{- j ω}) e^{- i ω t}$ si287_e as the response to cos(ωn) and substituting for H and ω = 2 gives

$y_{n} = \frac{1}{2} (\frac{e^{j 2} e^{j 2n}}{e^{j 2} + 0.2} + \frac{e^{- j 2}}{e^{- j^{2}} + 0.2} e^{- j 2 n})$

Expressing this over a real denominator and simplifying gives

$\frac{cos (2 n) (1 + 0.2 cos (2)) + 0.2 sin (2) sin (2 n)}{1.4 + 0.4 cos (2)}$

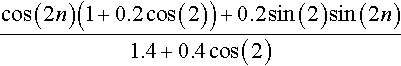
si289_e

Hence, the steady state response to an input of 3 cos(2n) is

$\frac{3 cos (2 n) (1 + 0.2 cos (2)) + 0.6 sin (2) sin (2 n)}{1.4 + 0.4 cos (2)} .$

si290_e

15.10 Summary

1. The Laplace transform F (s) of the function f (t) defined for t ≥ 0 is:

$F (s) = \int_{0}^{\infty} e^{- s t} f (t) d t .$

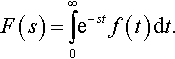
si291_e

The Laplace transform is a function of s, where s is a complex variable. Because the integral definition of the Laplace transform involves an integral to ∞, it is usually necessary to limit possible values of s so that the integral above converges (i.e. does not tend to ∞).

2. The impulse function, δ(t), also called a delta function, is the most famous example of a generalized function. The impulse function represents an idealized kick as it lasts for no time at all and has energy of exactly 1.

3. Laplace transforms are usually found by using a table of transforms (as in Table 15.1) and also by using properties of the transform, some of which are listed in Section 15.4.

4. Laplace transforms are used to reduce a differential equation to a simple equation in s-space. This can then be solved and the inverse transform used to find the solution to the differential equation.

5. The transfer function of the system, H (s), is the Laplace transform of its impulse response function with zero initial conditions, h(t). The Laplace transform of the response to any input function, with zero initial conditions, can be found by multiply the Laplace transform of the input function by the transfer function of the system Y (s) = H(s)F(s).

6. The steady state response to a single frequency input e^j^ω^t is H (jω)e^j^ω^t. H (jω) is called the frequency response function.

7. The z transform of a sequence f₀, f₁, f₂,…, f_n,.. is given by

$F (z) = \sum_{n = 0}^{\infty} f_{n} z^{- n} .$

si292_e

As this is an infinite summation it will not always converge. The set of values of z for which it exists is called the region of convergence.

8. The discrete impulse function or delta function is defined by

$δ_{n} = {\begin{matrix} 1 & n = 0 \\ 0 & n \neq 0. \end{matrix}$

si293_e

9. z transforms are usually found by using a table of transforms (as in Table 15.2) and also by using properties of the transform, some of which are listed in Section 15.7

10. z transforms are used to reduce a difference equation to a simple equation in z-space. This can then be solved and the inverse transform used to find the solution to the difference equation.

11. The transfer function of a discrete system, H (z), is the z transform of its impulse response function with zero initial conditions, h_n. The z transform of the response to any input function, with zero initial conditions, can be found by multiply the z transform of the input function by the transfer function of the system, Y (z) = H(z) F(z).

12. The steady state response of a discrete system to a single frequency input e^j^ωⁿ is H (e^jω)e^jωn. H (e^jωn) is called the frequency response function.

15.11 Exercises

15.1 Using the definition of the Laplace transform

$L {f (t)} = \int_{0}^{\infty} e^{- s t} f (t) d t$

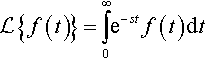
si294_e

show the following. In each case specify the values of s for which the transform exists.

(a) $L {2 e^{4 t}} = \frac{2}{s - 4}$ si295_e

(b) $L {3 e^{- 2 t}} = \frac{3}{s + 2}$

(d) $L {3 cos (5 t)} = \frac{3 s}{s^{2} + 25}$

15.2. Find Laplace transforms of the following using Table 15.1:

(a) $5 sin (3 t)$

(b) $cos (\frac{t}{2})$ si300_e

(d) $\frac{1}{2} e^{- 5 t}$

15.3. Find inverse Laplace transforms of the following using tables:

(a) $\frac{1}{s - 4}$

(b) $\frac{3}{s + 1}$

(d) $\frac{2}{s^{2} + 3}$

(e) $\frac{4 s}{9 s^{2} + 4}$

(f) $\frac{1}{s^{3}}$

(g) $\frac{5}{s^{4}}$

15.4. Find Laplace transforms of the following using the properties of the transform:

(a) $t e^{- 3 t}$

(b) $4 sin (t) e^{- 2 t}$

(d) $u (t - 1)$

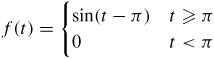
(e) $f (t) = {\begin{matrix} sin (t - π) & t \geq π \\ 0 & t < π \end{matrix}$ si314_e

15.5. Find inverse Laplace transforms of the following using the properties of the transform:

(a) $\frac{1}{{(s - 2)}^{2} + 9}$

(b) $\frac{s + 4}{{(s + 4)}^{2} + 1}$

(d) $\frac{s - 1}{s^{2} - 2 s + 10}$

15.6. Find inverse Laplace transforms using partial fractions:

(a) $\frac{1}{s (s + 1)}$

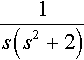
(b) $\frac{1}{s (s^{2} + 2)}$ si320_e

(d) $\frac{4}{(s^{2} + 1) (s - 3)}$

15.7. In each case solve the given differential equation using Laplace transforms:

(a) y’ + 5y = 0, where y(0) = 3

(b) y’ + y = t, where y(0) = 0

(d) y” −3y + 2y = 4e^2t, where y(0) = −3,y’(0) = 5

(e) y” + y = t, where y(0) = 1, y’(0) = −2

(f) y” + y‘ + 2y = 4,y(0) = 0,y’(0) = 0

15.8. A capacitor of capacitance C in an RC circuit, as in Figure 15.7, is charged so that initially its potential is V₀. At t = 0, it begins to discharge. Its charge q is then described by the differential equation

$R \frac{d q}{d t} + \frac{q}{C} = 0$

Using Laplace transforms, find the charge on the capacitor at time t after the switch was closed.

f15-07-9780750658553 — Figure 15.7 An RC circuit for Exercise 15.8.

15.9. Find the response of a system with zero initial conditions to an input of f (t) = 2e^−3t, given that the impulse response of the system is h(t) = 1/2(e^−t – e^−2t).

15.10.

(a) The impulse response of a system is given by h(t) = 3e⁻⁴^t. Find the system's step response, that is, the response of the system to an input of the step function, u(t).

(b) Use the result that Y(s) = H(s)F(s) where Y is the Laplace transform of the system output, F(s) the Laplace transform of the input and H(s) the system transfer function to show that the step response can be found by

$y_{u} (t) = L^{- 1} {\frac{H (s)}{s}}$

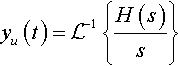
si324_e

$- \frac{4}{3} u (t) - e^{- 2 t} - \frac{2}{3} e^{- 3 t}$

si325_e

then

(i) find the system's transfer function; and

(ii) find its response to an input of e^−t.

15.11. A system has a known impulse response of h(t) = e^−t sin(2t). Find the input function f (t) that would produce an output of

$\begin{array}{l} y (t) = - 0.16 u (t) + 0.4 t + 0.16 e^{- t} cos (2 t) \\ ? ? ? ? ? ? ? ? ? ? ? ? ? ? - 0.04 sin (2 t) e^{- t} \end{array}$

si326_e

given zero initial conditions.

15.12. A system has transfer function

$H (s) = \frac{1}{{(s + 2)}^{2} + 4}$

si327_e

(a) Find its steady state response to a single frequency input of e^j5t;

(b) Find the steady-state response to an input of cos(5t) and sin(5t).

15.13. Using the definition of the z transform

$Z {f_{n}} = \sum_{n = 0}^{\infty} f_{n} z^{- n} = F (z)$

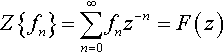
si328_e

show the following. In each case specify the values of z for which the transform exists:

(a) $Z {3 δ_{n}} = 3$

(b) $Z {6 u_{n}} = \frac{6 z}{z - 1}$

15.14. Find z transforms of the following using Table 15.2:

(a) $2 u_{n} + \frac{1}{2} n$

(b) $cos (3 n) + 2 sin (3 n)$

(d) $2 e^{j 4 n}$

15.15. Find inverse z transforms of the following using Table 15.2:

(a) $\frac{2 z}{z - 1} + 2$

(b) $\frac{z}{2 {(z - 1)}^{2}} + \frac{1}{1 + 3 / z}$

(d) $\frac{z^{2} + z (sin (1) - cos (1))}{z^{2} - 2 z cos (1) + 1}$

15.16. Find z transforms of the following using the properties of the transform:

(a) $u_{n + 2} 3^{n + 2}$

(b) ${(\frac{1}{2})}^{n} n$

(d) $n^{3}$

15.17. Find inverse z transforms of the following using the properties of the transform:

(a) $\frac{z}{{(z - 4)}^{2}}$

(b) $\frac{z}{z - 2 e^{j 4}}$

(d) $\frac{z}{z - 1} \frac{2 z}{z - 2}$

15.18. Find inverse z transforms using partial fractions

(a) $\frac{z^{2}}{(z - 1) (z + 1)}$

(b) $\frac{z^{3}}{(z - 1) (z^{2} - 2)}$

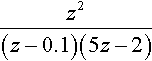
(d) $\frac{z^{2}}{{(z - 1)}^{2} (z + 2)}$

(e) $\frac{z^{2}}{z^{2} + 1}$

15.19 In each case solve the given difference equation using z transforms, n ≥ 0

(a) y_n + 5y_n−1 = 0, where y₋₁ = 3;

(b) $y_{n} + y_{n - 1} = n, ? where ? y_{- 1} = 0;$

(d) y_n −3y_n−1 + 2y_n−2 = 4 × 2ⁿ, where y_–1 = −3, y_–2 = 5;

(e) y_n + y_n–₁ = n, where y₋₁ = 0, y_–2 = 0

(f) 10y_n – 3y_n−1 – y_n–2= 4, y_–1= −1, y₋₂ = 2.

15.20. Find the response of a system with zero initial conditions, to an input of f_n = ₂(0.3)ⁿ, given that the impulse response of the system is h_n = (0.1)ⁿ + (−0.5)ⁿ.

15.21

(a) The impulse response of a discrete system is given by h_n=(0.8)ⁿ. Find the system's step response, that is, the response of the system to an input of the step function, u_n.

(b) Use the result that y(z) =H(z)F(z), where Yis the z transform of the system output, F (z) is the z transform of the input and H (z) is the system transfer function to show that the step response can be found by

$y_{n} = Z^{- 1} {\frac{H (z) z}{z - 1}}$

$\frac{1}{24} {(0.2)}^{n} + \frac{10}{48} u_{n}$

si355_e

then

(i) find the system's transfer functions; and

(ii) find its response to an input of 6(0.5)ⁿ.

15.22. A system has a known impulse response of h_n = (0.5)n. Find the input function f_n that would produce an output of 2(0.5)ⁿ+ 2_n −2u_n given zero initial conditions.

15.23. A system has transfer function H (z) = z/ (10z −3)

(i) find its steady state response to a single frequency input of e^j5i;

(ii) find the steady state response to an input of cos(5n) and sin(5n).

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 15.8 Solving linear difference equations with constant coefficients using z transforms

Create new playlist

Sign In

Sign Up

Using partial fractions to find the inverse transform

Example 15.29

15.8 Solving linear difference equations with constant coefficients using z transforms

Example 15.30

Example 15.31

15.9 z transforms and systems theory

The transfer function and impulse response function

Example 15.32

Response of a system with zero initial conditions to any input fn

Example 15.33

The frequency response

Example 15.34

15.10 Summary

15.11 Exercises

Table of Contents for
15.8 Solving linear difference equations with constant coefficients using z transforms

Response of a system with zero initial conditions to any input f_n