Vectors
9.1 Introduction
Many things can be represented by a simple number, for instance, time, distance, mass, which are then called scalar quantities. Others, however, are better represented by both their size, or magnitude, and a direction. Some of these are velocity, acceleration, and force. These quantities are called vector quantities because they are represented by vectors.
A simple example of a vector is one that describes displacement. Supposing someone is standing in a room with floor tiles (as in Figure 9.1) and moving from one position to another can be described by the number of tiles to the right and the number of tiles towards the top of the page.

In the example, to move from the door to the cupboard can be represented by (4, 2). This vector consists of two numbers, where the order of the numbers is important. Moving (4, 2) results in a different final position to that if we move (2, 4). The magnitude of the displacement can be found by drawing a straight line from the starting position to the final position and measuring the length. From Pythagoras theorem this can be found as ![]() . The direction can be described by an angle, for instance, the angle made to the wall with the window on it.
. The direction can be described by an angle, for instance, the angle made to the wall with the window on it.
This example shows that a two-dimensional vector (2D) can be used to represent movement on a flat surface. A 2D vector is two numbers, where the order of the numbers is important.
If the room in Figure 9.1 also had wall tiles then we could represent a position above the floor by the number of tiles towards the ceiling. This three-dimensional (3D) vector can be represented by three numbers. It can also be represented by the distance travelled and the direction, angles made to the floor and the angle made to the wall.
Velocity is an example of a vector quantity. This can be described by two things, the speed, which is the rate of change of distance travelled with respect to time, and also the direction in which it is travelling. Similarly, force can be described by the size of magnitude of the force and also the direction in which it operates.
Vectors have their own rules for addition and subtraction. If two forces of equal magnitude operate on one object then the net effect will depend on the direction of the forces. If the forces operate in opposite directions they could balance each other out, like two tug-of-war teams in a stalemate struggle. Alternatively, they could operate in the same direction or partially in the same direction and cause the object to have an acceleration.
For the examples of vectors given so far, the maximum dimension of the vector is three as there are only three spatial dimensions. However, there are many examples when vectors of higher dimension are useful. For instance, a path through the network given in Figure 9.2 can be represented by a list of 1 s and 0s to indicate whether each of the edges is included in the path. A path from S to T can be represented by a vector, for instance:


Although there are many other types of vectors we will concentrate on vectors of two or three dimensions, called spatial or geometrical vectors, used to represent physical quantities in space. Many of the ideas in this chapter are only true for geometrical vectors of two and three dimensional. As 3D vectors can only be correctly represented by making a 3D model, it is important to concentrate on understanding 2D vectors as they can be drawn on a piece of paper allowing results to be checked easily.
9.2 Vectors and vector quantities
A vector is a string of numbers, for example,
(1,0)
(3, −4, 2, −6, 8)
(2.6,9, −1.2,0.3).
The length of the string is called the dimension of the vector. For the examples given above, the dimensions are 3, 2, 5, and 4, respectively. The commas can be left out, so the examples given above can be written as
(1 0)
(3 −42 −6 8)
(2.69 −1.20.3).
Vectors may also be written as columns, giving:
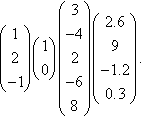
Whether vectors are written as columns or rows only becomes important when we look at matrices (Chapter 13). However, the order of the numbers in the vector is important: (0, 1) is a different vector from (1, 0).
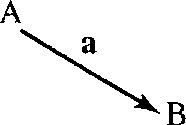
We will mainly deal with 2D or 3D vectors. Vectors are represented in a diagram by a line segment with an arrow as in Figure 9.3. In printed material vectors can be represented by bold letters: a. They are also represented by a or ![]() or
or ![]() , where A and B are points at either end of the vector.
, where A and B are points at either end of the vector.
In the rest of this chapter, we will assume that we are dealing with 2D or 3D vectors represented in rectangular form, also called Cartesian form.
This means that the numbers in the vectors correspond to the x, y, z values for a set of rectangular axes, as shown in Figure 9.4. This assumption is important for many of the geometrical interpretations presented here.

Position vectors and translation vectors
Vectors can represent points in a plane, as in Figure 9.5(a), or points in space, as in Figure 9.5(b). These are called position vectors. They can be thought of as representing a translation from the origin.
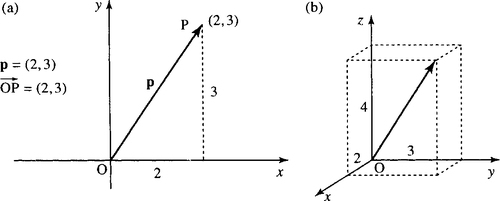
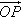 = (2,3) is used to represent a point in the plane. The point can be found by translating from the origin by 2 in the x-direction followed by 3 in the y-direction; hence, p = (2,3). (b) The position vector p = (2,3,4) is used to represent a point in space. The point can be found by translating from the origin by 2 in the x-direction, followed by 3 in the y-direction, and by 4 in the z-direction; hence, p = (2, 3, 4).
= (2,3) is used to represent a point in the plane. The point can be found by translating from the origin by 2 in the x-direction followed by 3 in the y-direction; hence, p = (2,3). (b) The position vector p = (2,3,4) is used to represent a point in space. The point can be found by translating from the origin by 2 in the x-direction, followed by 3 in the y-direction, and by 4 in the z-direction; hence, p = (2, 3, 4).Vectors can represent a translation that can be applied to figures. In Figure 9.6, a four-sided figure ABCD has been translated through the vector (2, 3).

Vector quantities
Vectors can represent physical quantities that have both a magnitude and a direction. In Figure 9.7, there is an example of the forces acting on a body that is being pulled up a slope. By using vectors and vector addition the resultant force acting on the body can be found and therefore the direction in which the body will travel can be found together with the size of the acceleration. Other quantities with both magnitude and direction are velocity, acceleration, and moment. Quantities that only have magnitude and no direction are called scalar quantities and can be represented using a number, for example, mass and length.

9.3 Addition and subtraction of vectors
Addition
To add two vectors, add the corresponding elements of the vectors.
Example 9.1
a + b = (2,3) + (4,2) = (2 + 4,3 + 2) = (6,5)
c = (1,3,1.5) d = (5, −2,1)
c+ d = (1,3,1.5)+(5,−2,1) = (1+5,3+(−2),1.5+1) = (6,1,2.5).
If the vectors are represented in the plane then the vector sum can be found using the parallelogram law, as in Figure 9.8. The resultant or vector sum of a and b is found by drawing vector a and then drawing vector b from the tip of vector a which gives the point C. Then a + b can be found by drawing a line starting at O to the point C. If we imagine walking from O to A, along vector a, and then from A to C, along vector b, this has the same effect as walking direct from O to C, along vector c. We can also use the parallelogram to show that a + b = b + a. To find b + a, start with vector b and draw vector a from the tip of vector b; this also gives the point C. Then if we walk from O to B along vector b and then from B to C along vector a, this has the same effect as walking along the other two sides of the parallelogram or walking direct from O to C. Hence

a+b=b+a=c
Subtraction
To subtract one vector from another, subtract the corresponding elements of the vectors.
Example 9.2
a − b = (2,3) − (4,2) = (2–4,3–2) = (−2,1).
Using a vector diagram we can perform vector subtraction in two ways. Draw a and −b and add as before or simply draw vectors a and b from the same point and the line joining the tip of b to the tip of a gives the vector a−b. These methods are explained in Figure 9.9.
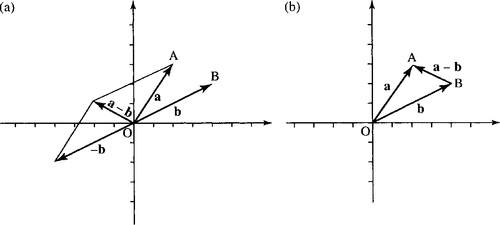
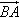 gives the vector a–b. To see this imagine walking directly from B to A, this is the same as walking from B to O, which is backwards along b and therefore is the vector –b, and then along
gives the vector a–b. To see this imagine walking directly from B to A, this is the same as walking from B to O, which is backwards along b and therefore is the vector –b, and then along 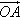 which is the vector a. Hence,
which is the vector a. Hence,  = –b + a = a–b.
= –b + a = a–b.Example 9.3
In Figure 9.10, ![]() = a and
= a and ![]() = b. OB = BC,OA = EO, and AD is parallel to OC and EF. Write the following vectors in terms of a and b:
= b. OB = BC,OA = EO, and AD is parallel to OC and EF. Write the following vectors in terms of a and b:
![]()

Solution
(a) ![]() is the same length as a in the opposite direction; therefore,
is the same length as a in the opposite direction; therefore, ![]() = –a.
= –a.
(b) ![]() is in the same direction as b, but twice the length; therefore,
is in the same direction as b, but twice the length; therefore, ![]() = 2b.
= 2b.
(c) ![]() is in a triangle with a and b. To get from B to A we would walk in the reverse direction along b and then along a:
is in a triangle with a and b. To get from B to A we would walk in the reverse direction along b and then along a: ![]() = −b + a = a− b.
= −b + a = a− b.
(d) ![]() = –
= – ![]() = –(a − b) = b – a.
= –(a − b) = b – a.
(e) ![]() is parallel to
is parallel to ![]() in the same direction; therefore, as
in the same direction; therefore, as ![]() = 2b then
= 2b then ![]() = 2b.
= 2b.
(f) To find ![]() we need to know
we need to know ![]() .
.![]() is the same length as a in the opposite direction; therefore,
is the same length as a in the opposite direction; therefore, ![]() = –a. To get from B to E we could go from B to O (–b) and then from O to E (–a); therefore,
= –a. To get from B to E we could go from B to O (–b) and then from O to E (–a); therefore, ![]() = −b − a.
= −b − a.
(g) ![]() is the same length as
is the same length as ![]() and in the same direction; therefore,
and in the same direction; therefore, ![]() =
= ![]() = b –a.
= b –a.
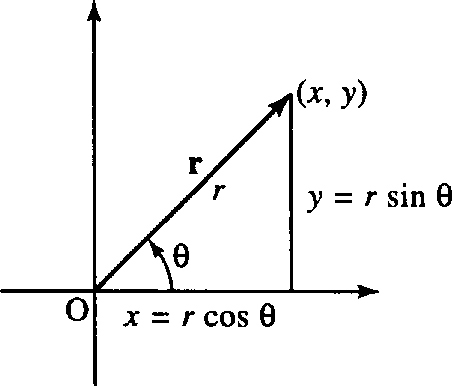
9.4 Magnitude and direction of a 2D vector–polar co-ordinates
We have already noted that a vector has magnitude and direction. A 2D vector can be represented by its length (also called magnitude or modulus), r (or |r|), and its angle to the x-axis, also called its argument, θ. If the vector is (x, y) then r2= x2 + y2, from Pythagoras's theorem The angle is given by tan−1 (y / x) if x is positive and by tan−1 (y / x) + π if x is negative. Hence, r = (r, θ) in polar coordinates, and can also be written as r ∠θ so it is clear that the second number represents the angle. As it is usual to give the angle between –π and +π, it may be necessary to subtract 2π from the angle given by this formula. (As a rotation of 2π is a complete rotation this will make no difference to the position of the vector.)
Example 9.4
Find the magnitude and direction of
(b) (–1, – 4)
(c) (1, −2.2)
(d) (–2, 5.6)
Solution To perform these conversions to polar form it is a good idea to draw a diagram of the vector in order to be able to check that the angle is of the correct size. Figure 9.11 shows the diagrams for each part of the example.

(a) r = (2, 3) has magnitude ![]() ≈ 3.606 and angle given by tan−1(3/2) ≈ 0.983 and therefore in polar coordinates r is 3.606 ∠0.983.
≈ 3.606 and angle given by tan−1(3/2) ≈ 0.983 and therefore in polar coordinates r is 3.606 ∠0.983.
(b) r = (−1, −4) has magnitude r = ![]() , and angle given by tan−1(−4/−l)+π ≈1.326+3.142 = 4.467. As this angle is bigger than π, subtract 2π (a complete revolution) to give −1.816. Therefore, in polar co-ordinates r = 4.123 ∠ −1.816. Note that the angle is between –π and − π /2, meaning that the vector must lie in the third quadrant, which we can see is correct from the diagram.
, and angle given by tan−1(−4/−l)+π ≈1.326+3.142 = 4.467. As this angle is bigger than π, subtract 2π (a complete revolution) to give −1.816. Therefore, in polar co-ordinates r = 4.123 ∠ −1.816. Note that the angle is between –π and − π /2, meaning that the vector must lie in the third quadrant, which we can see is correct from the diagram.
(c) r = (1, −2.2) has magnitude ![]() and the angle is given by tan−1 (−2.2/1) ≈ −1.144. Therefore, in polar co-ordinates r = 2.416 ∠−1.144. Note that the angle is between −π /2 and 0, meaning that the vector must lie in the fourth quadrant.
and the angle is given by tan−1 (−2.2/1) ≈ −1.144. Therefore, in polar co-ordinates r = 2.416 ∠−1.144. Note that the angle is between −π /2 and 0, meaning that the vector must lie in the fourth quadrant.
(d) r = (−2,5.6) has magnitude ![]() and angle given by tan−l (5.6/ – 2) +π ≈1.914. Therefore, in polar co-ordinates r = 5.946 ∠1.914. Note that the angle is between π/2 and π, meaning that the vector must lie in the second quadrant.
and angle given by tan−l (5.6/ – 2) +π ≈1.914. Therefore, in polar co-ordinates r = 5.946 ∠1.914. Note that the angle is between π/2 and π, meaning that the vector must lie in the second quadrant.
Many calculators have a rectangular to polar conversion facility. Look this up on the instructions with your calculator and check the results. Remember, to get the result in radians you should first put your calculator into radian mode.
Conversion from polar co-ordinates to rectangular co-ordinates
If a vector is given by its length and angle to the x-axis, that is, r = r ∠θ, then
![]()
Hence, in rectangular co-ordinates r = (r cos (θ), r sin (θ)).
This result can easily be found from the triangle, as shown in Figure 9.12; examples are given in Figure 9.13.

Adding two vectors expressed in polar co-ordinates
To add two vectors expressed in polar co-ordinates, first express them in rectangular co-ordinates, then find the sum and then convert back into polar co-ordinates.
Example 9.5
Find 2 ∠20° + 4 ∠50°.
Solution Using x = r cos(θ) and y = r sin(θ), we can express the two vectors in rectangular co-ordinates, giving
4 ∠50° ≈ (2.5711,3.064).
Therefore, 2 ∠20° + 4 ∠50° ≈ (1.879,0.684) + (2.571,3.064) = (4.45,3.748).
Finally, this can be represented in polar co-ordinates by using ![]() and θ = tan −1 (y / x) (+π, if x is negative) giving (4.45, 3.748) ≈ 5.818 ∠40.106°.
and θ = tan −1 (y / x) (+π, if x is negative) giving (4.45, 3.748) ≈ 5.818 ∠40.106°.
Example 9.6
Find 4 ∠1 + 2 ∠−1.6.
Solution Using x = r cos (θ) and y = r sin (θ), we can express the two vectors in rectangular co-ordinates, giving 4 ∠1≈ (2.161, 3.366):
2 ∠−1.6 ≈(−0.058, −1.999).
Therefore, 4∠1 +2∠ −1.6 ≈ (2.161,3.366) + (−0.058,−1.999) = (2.103, 1.367).
Finally, this can be represented in polar co-ordinates by using ![]() and θ = tan−1 (y / x) (+π, if x is negative), giving (2.103, 1.367) ≈ 2.508 ∠0.576.
and θ = tan−1 (y / x) (+π, if x is negative), giving (2.103, 1.367) ≈ 2.508 ∠0.576.
9.5 Application of vectors to represent waves (phasors)
In Section 5.3, we found the amplitude, phase, and cycle rate (frequency) of a wave. f(t) = A cos(ωt + ϕ) has amplitude A, angular frequency ω and phase ϕ. Suppose we consider waves of a fixed frequency (say 50 Hz giving ω = 50 × 2π ≈ 314); then, different waves can be represented by the amplitude and phase, giving y = A∠ϕ. The ideas of vectors can then be used to add and subtract waves and find their combined effect.
If a wave can be represented in polar form by A∠ϕ, then what does the rectangular form of the vector represent? We find that if the wave is split into cosine and sine terms by using the trigonometric identity cos(A + B) = cos(A) cos(B) – sin(A) sin(B), we get:
f(t) = A cos (ωt + ϕ) = A cos (ϕ) cos (ωt) — A sin (ϕ) sin (ωt).
As A cos (ϕ) is a constant, not involving an expression in t, this can be replaced by c and similarly A sin (ϕ) can be replaced by d giving
f(t) = c cos(ωt) — d sin(ωt)
where c = A cos(ϕ) and d = A sin(ϕ).
So the vector (c, d) used to represent a wave represents the function f(t) = c cos(ωt) — d sin(ωt) and if expressed in polar form A∠ϕ it represents the equivalent expression
f(t) = A cos(ωt+ϕ)
Example 9.7
Express the following as a single cosine term and give the amplitude and phase of the resultant function:
x = 3 cos(2t) + 2 sin(2t).
Solution Comparing x = 3 cos(2t) + 2 sin(2t) with the expression f(t) = c cos(ωt) – d sin(ωt) gives c = 3, d = −2 and ω = 2. Expressing the vector (3, −2) in polar form gives 3.605∠−0.588 and hence x = 3.605 cos(2t – 0.588) giving the amplitude as 3.605 and phase as –0.588.

which is the original expression.
Example 9.8
Express the following as a single cosine term and hence give the magnitude and phase of the resultant function:
y = −2 cos(t) – 4 sin(t)
Solution Comparing y = −2 cos(t) – 4 sin(t) with the expression f(t) = c cos(ωt) – d sin(ωt) gives c = −2, d = 4, and ω = 1. Expressing the vector (−2, 4) in polar form gives 4.472 ∠ 2.034 and hence y = 4.472 cos(t + 2.034).
Check: Expand y = 4.472 cos(t + 2.034) using cos(A + B) = cos(A) cos(B) – sin(A) sin(B) : 4.472 cos(t + 2.034) = 4.472 cos(t) cos(2.034) – 4.472 sin(t) sin(2.034) = −2 cos(t) – 4 sin(t).
Example 9.9
Express x = 3 cos(20t + 5) as the sum of cosine and sine terms.
Solution On representing x as the phasor 3 ∠5 with angular frequency 20,3 ∠5 converts to rectangular form as the vector (0.851, −2.877) and this now gives the values of (c, d) in the expression f(t) = c cos(ωt) – d sin(ωt), giving x = 0.851 cos(20t) + 2.877 sin(20t).
Example 9.10
Find the resultant wave found from combining the following into one term:
f(t) = 3 cos(314t + 0.5) + 2cos(314t + 0.9).
Solution As both terms are of the same angular frequency, 314 radians s−1, we can express the two component parts by their amplitude and phase and then add the two vectors, giving 3 ∠0.5+2 ∠0.9.
Expressing these in rectangular form gives (2.633, 1.438) + (1.243,1.567) = (3.876,3.005).
Finally, expressing this again in polar form gives 4.904 ∠ 0.659, so the resultant expression is f(t) = 4.904 cos(314t + 0.659).
This method is a shorthand version of writing out all the trigonometric identities. It is even quicker if you use the polar – rectangular and rectangular – polar conversion facility on a calculator.
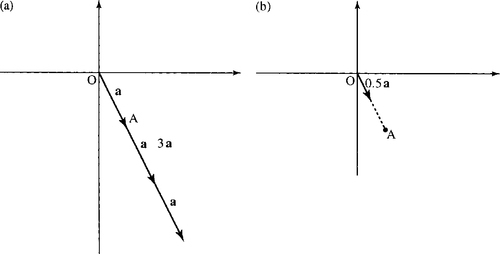
9.6 Multiplication of a vector by a scalar and unit vectors
Multiplying a vector by a scalar has the effect of changing the length without affecting the direction. Each number in the vector is multiplied by the scalar
Example 9.11
If a = (1, −2) then
3a = 3 (1, −2) = (3 × 1,3 × (–2)) = (3, −6)
0.5a = 0.5(1, −2) = (0.5 × 1,0.5 × (−2)) = (0.5, −1).
This is shown in Figure 9.14.
Unit vectors
Unit vectors have length 1. They are often represented by vectors with a cap on them ![]() Hence,
Hence, ![]() means the unit vector in the same direction as r. To find the unit vector in the same direction as r, divide r by its length:
means the unit vector in the same direction as r. To find the unit vector in the same direction as r, divide r by its length: ![]() = r /|r|, where |r| represents the magnitude of vector r.
= r /|r|, where |r| represents the magnitude of vector r.
In Section 9.5, we found the length of a 2D vector (x, y) is ![]() , similarly it can be shown that in three dimensions (x,y, z) the length is
, similarly it can be shown that in three dimensions (x,y, z) the length is ![]() .
.
Example 9.12
Find unit vectors in the direction of the following vectors:
(a) (1, −1) (b) (3, 4) (c) (0.5, 1, 0.2).
Solution (a) Find the length of (1, −1) given by ![]() =
= ![]() . Therefore, the unit vector is
. Therefore, the unit vector is
![]()
(b) Find the length of (3, 4) given by ![]() =
= ![]() = 5. Therefore, the unit vector (see Figure 9.15) is
= 5. Therefore, the unit vector (see Figure 9.15) is
![]()

 . The unit vector in the same direction is found by dividing the vector r by its length giving
. The unit vector in the same direction is found by dividing the vector r by its length giving 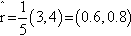 .
.(c) Find the length of (0.5, 1, 0.2) given by ![]() =
= ![]() . Therefore, the unit vector is
. Therefore, the unit vector is ![]() .
.
9.7 Basis vectors
Vectors in a plane are made up of a part in the x-direction and a part in the y-direction, for example, (2,3) = (2,0) + (0,3). i and j are used to represent unit vectors in the x-direction and y-direction, that is, i = (1,0) and j = (0, 1).
Any vector in the plane can be expressed in terms of i and j. i and j are called the Cartesian unit basis vectors, which is the name given to a co-ordinate system where the axes are at right angles to each other (orthogonal) (see Figure 9.16):
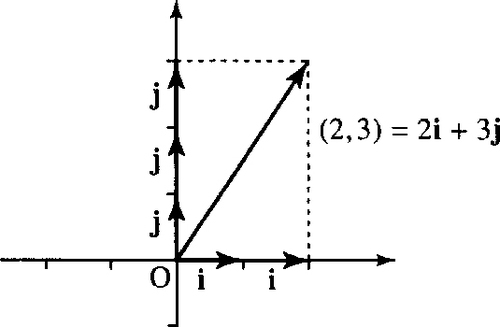
(2,3) = 2(1,0) + 3(0, 1) = 2i + 3j.
The unit vector in the z direction is often given the symbol k; and in three dimensions, using rectangular axes we have:
i = (1, 0, 0) j = (0, 1, 0) k = (0, 0, 1)
that is
(5, −1,2) = (5,0,0) + (0, −1,0) + (0,0,2)
= 5(1,0,0) + (–1)(0,1,0) + 2(0,0,1)
= 5i – j + 2k.
The vectors i and j form a basis set because all 2D geometrical vectors can be expressed in such terms. Similarly, all 3D vectors can be expressed in terms of i, j, and k. There are many other sets of vectors that can be used as a basis set: for instance, if we were in a room shaped like a parallelogram we could express any position in the room by moving parallel to one of the sides and then parallel to the other side. This is shown in Figure 9.17. Other basis sets are not as useful for interpreting spatial vectors as they do not give the same geometrical results. For instance, the interpretation of the scalar product, given in Section 9.8, relies on the fact that we use Cartesian basis vectors.

9.8 Products of vectors
There are two products of vectors that are commonly used: the scalar product, which results in a scalar, and the vector or cross product, which gives a vector as the result. However, both of these products are irreversible: they have no inverse operation. In other words, it is not possible to divide by a vector.
Scalar product
The scalar product of two vectors is defined by
a · b = (a1, a2) · (bl · b2) = a1b1 + a2b2.
Notice that the scalar product gives a simple number as the result.
Example 9.13
Find the scalar product of (2, 3) and (1, 2).
Solution Using the definition
(2, 3) ⋅ (1, 2) = (2)(1) + (3)(2) = 2 + 6 = 8.
Interpretation of the scalar product
The scalar product of a and b is related to the length of the vectors in the following way: a · b = ab cos(θ), where θ is the angle between the two vectors and a is the magnitude of a and b is the magnitude of b (see Figure 9.18).

The magnitude of a vector is the square root of the dot product with itself; hence, a · a = a2.
The scalar product can be used to find the angle between two vectors. It can also be used to find the length of a vector and can be used to test if two vectors are at right angles (orthogonal).
Example 9.14
Find the angle between (1, −1) and (3,2).
Solution If a = (1, −1) and b = (3,2), then a · b = (1, −1) · (3,2) = (1)(3) + (−1)(2) = 3 – 2 = 1.
We now use the relationship
![]()
to find the angle between the vectors. We find the magnitude of a and the magnitude of b
![]()
Hence,
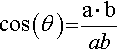
becomes
![]()
giving θ = cos−1(0.196) ≈ 1.373 radians.
Example 9.15
Show that (2, −1) and (−0.5, −1) are at right angles.
Solution If two vectors are at an angle θ with cos(θ) = 0, then θ = ±90°, so the vectors are at right angles. Hence, if we find that a · b = 0 this shows that a and b are at right angles (as long as one of the vectors is not the null vector (0, 0)). In this case the scalar product gives:
(2, −1)· (−0.5, −1) = 2(–0.5) + (–1)(–1) = −1 + 1 = 0
As the scalar product of the two vectors is 0 the angle between them is 90°, so they are at right angles.
Example 9.16
Show that (1, −1) and (−2, −2) are at right angles.
Solution (1, −1) · (–2, −2) = (1)(−2) + (–1)(–2) = −2 + 2 = 0
Hence, they are at right angles.
Direction cosines
We have seen that the scalar product of two vectors a and b, a · b = ab cos(θ). We can use this result to show that the components of a unit vector are the direction cosines of the vector, that is,
![]()
where α is the angle that the vector makes to the x-axis and β is the angle that the vector makes to the y-axis.
To show this, consider a unit vector ![]() = (x, y) = x i + y j. If we take the scalar product with the unit vector along the x-axis, i = (1,0), we will get
= (x, y) = x i + y j. If we take the scalar product with the unit vector along the x-axis, i = (1,0), we will get
![]()
and we know that ![]() · i = |
· i = |![]() ||i| cos(α), where
||i| cos(α), where ![]() and |i| are the magnitudes of
and |i| are the magnitudes of ![]() and i, respectively, and α is the angle between them. In this case, as we have two unit vectors their magnitudes are 1. This means that
and i, respectively, and α is the angle between them. In this case, as we have two unit vectors their magnitudes are 1. This means that ![]() · i = cos(α), where α is the angle between the two vectors. In this case, α is the angle that the vector,
· i = cos(α), where α is the angle between the two vectors. In this case, α is the angle that the vector, ![]() , makes to the x-axis. We have shown that
, makes to the x-axis. We have shown that ![]() · i = cos(α) and we know that
· i = cos(α) and we know that ![]() · i = x, so we have that x = cos(α), where α is the angle to the x-axis. By considering
· i = x, so we have that x = cos(α), where α is the angle to the x-axis. By considering ![]() · j, we find that y = cos(β), where β is the angle that the vector
· j, we find that y = cos(β), where β is the angle that the vector ![]() makes to the y-axis. So we have that the components of any unit vector
makes to the y-axis. So we have that the components of any unit vector ![]() are the direction cosines of the vector.
are the direction cosines of the vector.
If we consider any vector r we can find that a unit vector is the same direction as r by dividing by the magnitude of r. Hence, we have that:
![]()
where α is the angle the vector r makes to the x-axis and β is the angle the vector r makes to the y-axis (see Figure 9.19).

 = (cas(α), cas(β)) where α is the angle the vector r makes to the x-axis and β is the angle the vector r makes to the y-axis.
= (cas(α), cas(β)) where α is the angle the vector r makes to the x-axis and β is the angle the vector r makes to the y-axis.In three dimensions we get:
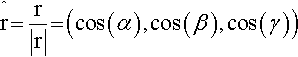
where α is the angle the vector r makes to the x-axis, β is the angle it makes to the y-axis, and γ the angle it makes to the z-axis.
Example 9.17
Find the angle that the following vectors make to the axes: (a) (3, 6); (b) (–1, −4,5).
Solution (a) r/|r = (cos(α), cos(β)), where α and β are the angles made to the x and y axes. Therefore,
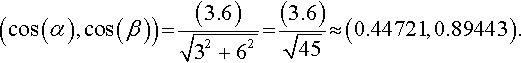
The angle made to the x-axis is α = cos−1(0.44721) ≈ 1.107 and the angle made to the y-axis is β = cos−1 (0.89443) ≈ 0.463. The angles made to the x and y axes are 1.107 and 0.463 radians, respectively.
(b) r/|r = (cos(α), cos(β), cos(y)), where α, β and γ are the angles made to the x, y, and z axes. Therefore,
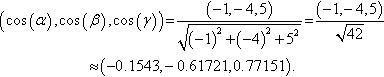
The angles made to axes in the x, y, and z directions are found by taking the inverse cosines of the above: 1.726, 2.236, 0.6896 radians, respectively.
Vector components
The scalar product can be used to find the component of a vector in a given direction. This is a useful idea, for instance, if we are resolving forces and we want to add up all the forces acting in a certain direction. We can use the dot product with a unit vector in the direction of interest to find the component in that direction. The component of a vector F in the direction of a vector r is F · (r /|r|)
Example 9.18
A removal company wants to move a piano from the upstairs window of a small house. A smooth plank is placed against a wall near the window so that it touches the wall at a height of 4 m and the base of the plank is 1.5 m from the building. The piano, of mass 800 kg, is to be slid down the plank while attached by a rope. Taking the acceleration due to gravity to be g ≈ 9.81 m s−2, what force is required on the other end of the rope to hold the piano steady while it is on the plank?
Solution We draw the situation as in Figure 9.20 using x and y axes. The vector that represents the plank goes from (0,0) to (1.5, 4). This is the direction vector p = (1.5,4) – (0,0) = (1.5,4).

The acceleration due to gravity is in a vertical direction and is a = (0, – g). From Newton's second law the force due to gravity is
F = m a= 800 × (0, −9.81).
The component of the force due to gravity acting along the direction of the plank is the scalar product of the force with a unit vector in the direction of the plank, that is

The – sign indicates that the component of the force due to gravity is in the opposite direction to the vector p along the plank. In order to hold the piano steady on the plank, we would need to have a force of equal magnitude in the opposing direction to be provided by the rope. That is, we would require a force of 7348 N on the rope.
Vector (or cross) product
The vector product of a and b is defined by a × b = ab sin (θ) ![]() , where
, where ![]() is the unit vector normal to the plane of a and b and θ is the angle between a and b.
is the unit vector normal to the plane of a and b and θ is the angle between a and b.
If a and b are vectors that lie in the x, y plane, the vector product will be a vector normal to that plane, that is, wholly in the z-direction. It can be found from the following expression:
(a1, a2, 0) × (b1, b2, 0) = (0,0, a1b2 − (a2b1) = (a1b2 −a2b1)k
where k is the unit vector in the z-direction.
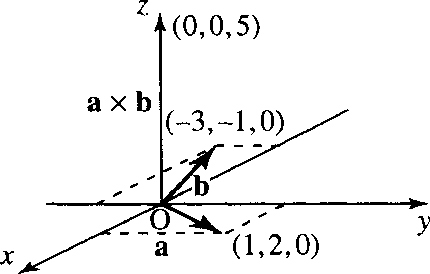
Example 9.19
(1,2,0) × (–3, −1,0) = (0,0, (1) (–1) – (2) (–3)) = (0, 0, 5). This is shown in Figure 9.21.
Applications of the vector product
The vector product can be used to find the area of a parallelogram with sides OA and OB (see Figure 9.22).
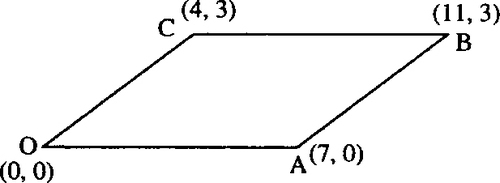
The area of a parallelogram is given by ab sin (θ), where a and b are the lengths of the sides and θ is the angle between them. Consider vectors a and b representing the sides of the parallelogram. We know that a × b = ab sin (θ)![]() , where
, where ![]() is a unit vector normal to the plane of a and b. As
is a unit vector normal to the plane of a and b. As ![]() is a unit vector it has a magnitude of 1, so |a × b| = ab sin (θ), which is exactly the same as the formula for the area of the parallelogram. Therefore, the area of the parallelogram can be found by taking the magnitude of the vector product of the vectors that define the sides of the parallelogram.
is a unit vector it has a magnitude of 1, so |a × b| = ab sin (θ), which is exactly the same as the formula for the area of the parallelogram. Therefore, the area of the parallelogram can be found by taking the magnitude of the vector product of the vectors that define the sides of the parallelogram.
As sin (θ) = 0 when θ = 0 or θ = 180o, the vector product can also be used to test for parallel vectors (vectors pointing in the same direction or in exactly opposing directions). Again we only need to consider the magnitude of the vector product.
Example 9.20
Show that the vectors (0.2, −5) and (–1,25) are parallel.
Solution Find 1(0.2, −5) × (–1,25) | = | (0.2 × 25) – (−5 × −1) | = 15–51=0.
As we know that |a × b| = ab sin (θ), then as a and b are of non-zero length, |a × b |= 0 ⇔ sin (θ) = 0. This shows that the vectors are parallel.
9.9 Vector equation of a line
In Chapter 2, we looked at the equation of a line that we found to be y = mx + c, where the gradient of the line is m and the line goes through the point (0, c). We also found that the equation of a line that goes through two points, (Xl, Y1) and (x2, y2), is
![]()
We would like to be able to express the equation of a line as a vector equation. If we know that the two points A and B represented by the position vectors a and b lie on the line, then a vector in the direction of the line will be a vector joining those two points, that is, b – a. As the line must go through A, we can see that any multiple of b – a added to the position vector a must lie on the line. This is shown in Figure 9.23

If we call the position vector of any point on the line r where r = (x, y), we now have the vector equation of the line as r = a + λ (b – a) where λ ∈ ![]() .
.
This can be rewritten as r = a (1 – λ) + λb.
Example 9.21
Find the vector equation of a line through the points (2, 4) and (0, 6) and show that your result agrees with the equation of the line y = −x + 6, as found in Example 2.3.
Solution Using r = a(1 – λ) + λb and a = (2,4), b = (0,6), we find r = (2,4)(1 – λ) + λ(0, 6) = (2(1 – λ) + λ(0), 4(1 – λ) + λ6) r = (2 – 2λ, 4 + 2λ)
To show that this is the same as equation y = –x + 6 use r = (x, y) (x, y) = (2 – 2λ, 4+2λ) ⇔ x =2 – 2λ and y = 4+2λ
This is a parametric equation for the line with parameter λ.
Eliminate λ by rewriting the equation for x so that λ is the subject and substitute into the equation for y:
![]()
Substituting for λ in y = 4 + 2λ gives
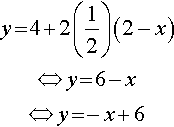
This shows that the vector equation of the line is equivalent to y = – x + 6.
9.10 Summary
1. A vector is a string of numbers where the length of the string is called the dimension of the vector.
2. Vectors are used to represent points on a plane or in space, translations and physical quantities that have both magnitude and direction (called vector quantities).
3. The vector sum is found by adding corresponding elements of the vectors, or from a diagram by using a parallelogram.
4. To subtract vectors, subtract corresponding elements of the vectors. A triangle may be used to perform vector subtraction in a diagram.
5. Two-dimensional vectors r = (x, y) can be expressed in polar co-ordinates using
![]()
and θ = tan−1(y) (+π, if x is negative), so that (x, y) = r∠θ where r or |r|is the magnitude, or length, of the vector and θ is theangle that the vector makes to the x-axis, also called its argument. To convert from polar to rectangular co-ordinates use:
![]()
To add vectors given in polar form they must first be converted to rectangular form.
6. Waves of a fixed frequency can be represented by phasors giving the amplitude and phase. f(t)= A cos (ωt + ϕ) can be represented by its amplitude and phase A∠ϕ. Converting this vector to rectangular form gives (c,d) where
![]()
Using ideas of conversion from polar to rectangular form and vector addition, waves of the same frequency can be easily combined.
7. Unit vectors have length 1. To find the unit vector in the same direction as a vector r divide the vector by its length:
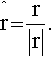
8. Any vectors in the plane can be represented in terms of i = (1, 0) and j = (0,1) and in three dimensions by i = (1,0, 0), j = (0,1,0), and k = (0,0, 1). These are the Cartesian unit basis vectors and they are at right angles to each other.
9. Where a = (a1, a2) and b = (b1,b2)are two vectors, the scalar product is given by a · b = (a1a2) ·(bl, b2) = a1b1+ a2b2and a ·b = ab cos(θ), where a, b are the magnitudes of the vectors a and b, and θ is the angle between them. The scalar product can be used to find the angle between two vectors.
10. The components of any unit vector give the cosines of the angles that the vector makes to each of the Cartesian axes. Then we have for any vector r:

where α is the angle the vector r makes to the x-axis and β is the angle it makes to the y-axis. In three dimensions:

where α is the angle the vector r makes to the x-axis, β is the angle it makes to the y-axis, and γ is the angle it makes to the z-axis. cos (α), cos (β), and cos (γ) are called the direction cosines of the vector.
11. The scalar product can be used to find the component of a vector in any given direction. Component of a vector F in the direction of a vector r = F · (r /|r|).
12. The vector product is given by a × b = ab sin (θ)![]() , where a and b are the magnitudes of the vectors a and b, θ is the angle between them, and
, where a and b are the magnitudes of the vectors a and b, θ is the angle between them, and ![]() is a unit vector normal to the plane of a and b. If a and b are vectors in the x, y plane, that is, a = (a1, a2, 0) and b = (bl, b2, 0), we have
is a unit vector normal to the plane of a and b. If a and b are vectors in the x, y plane, that is, a = (a1, a2, 0) and b = (bl, b2, 0), we have
(a1, a2, 0) × (bl, b2, 0) = (0,0, a1b2 –a2b1) = (alb2 – a2b1)k
where k is the unit vector in the z-direction. The magnitude of the vector product can be used to find the area of a parallelogram.
13. The vector equation of a line passing through two points a and b is
r = a(1 – λ) + λb λ ∈ ![]()
9.12 Exercises
9.1. In Figure 9.24, ![]() = a and
= a and ![]() = b, OA = BC = OD, OB = AC = EO, EOB and DOA are straight lines. Write the following in terms of a and b:
= b, OA = BC = OD, OB = AC = EO, EOB and DOA are straight lines. Write the following in terms of a and b:
(b) ![]()
(c) ![]()
(d) ![]()
(e) ![]()
(f) ![]()
(g) ![]()
(h) ![]()
(i) ![]()
(j) ![]()

9.2. Given a = (1,3), b = (–1,2), C = (3,6,2), and d = (6,4, −1), find the following:
(b) a – b
(c) b – a
(d) − b + a
(e) 2b
(f) a + 2b
(g) 3a – b
(h) c –d
(i) 10c
(j) c + 6d
(k) 6c – d
9.3. Express the following in its polar form, r ∠θ, where r is the length of the vector and θ its angle to the x-axis:
(b) (3, −1)
(c) (−1, −3)
(d) (5, −6)
9.4. Express the following vectors r ∠θ, where r is the modulus of the vector and θ the angle to the x-axis, in rectangular form. The angle is expressed in radians.
(b) l ∠ –π
(c) ![]() ∠π/4
∠π/4
(d) 3∠π/3
9.5. Express the following as a sum of a cosine and sine term in ωt:
(b) f(t) = 10 cos(20t + 5)
9.6. Express the following as single cosine terms:
(a) f(t) = 4 cos(10t) – 3 sin(10t)
(b) g(t) = −2 cos(157t)+ 10 sin(157t)
9.7. Express the following as a single wave:
(a) 6 cos(2t –3) + 10 cos(2t+ 2)
(b) cos(t –π /2) + cos(t + π /2)
(c) 2 cos(628t – 1.57) −6 cos(628t)
9.8. Find the unit vectors in the same direction as the following:
(b) (5, 12)
(c) (5, – 12)
(d) (1, 1)
(e) (3,2)
(f) (2,0)
(g) (0, −3)
(h) (2,4,4)
(i) (1, −1,2)
(j) (0.5,0, −0.5)
9.9. Express the following vectors in terms of i = (1,0) and j = (0, 1) or in terms of i = (0, 0, 1), j = (0, 1, 0), and k = (0, 0, 1) for 3D vectors:
(b) (–1, −2)
(c) (–6,2)
(d) (–1,2, −3)
(e) (0.2, −1.6,3.3)
9.10. Find the following scalar products:
(b) (9, 2) · (– 1, 6)
(c) (6, −1) · (−1, −3)
9.11. Find the angle between the following pairs of vectors:
(b) (6, −1) and (1,6)
(c) (2, −1) and (4,9)
9.12. Show that the following pairs of vectors are at right angles to each other:
(b) (–6,3) and (1,2)
(c) (0.5, −2) and (4, 1)
9.13. Find the angles that the following vectors make to the axes:
(b) (−1, −4,5)
9.14. (a) Find the component of the vector (−1,5) in the direction of the following vectors:
(ii) (0.5, −0.5)
(iii) (−5, 1)
(iv) (1, −5)
(v) (8,2)
(b) Find the component of the vector (−1, 2, 7) in the direction of the following vectors:
(ii) (6, 0, 2)
9.15. Show that the following pairs of vectors are parallel:
(b) (6,3) and (18,9)
9.16. Find the area of the parallelogram OABC where two adjacent sides are:
(b) ![]() = (4, −1) and
= (4, −1) and ![]() = (2,2)
= (2,2)
(c) ![]() = (−3, 1) and
= (−3, 1) and ![]() = (2,3)
= (2,3)
9.17. A straight line passes through the pair of points given. Find the vector equation of the line in each case:
(b) (1,1), (−2, −4)
(c) (1,1), (6,3)
(d) (−1, −4), (−3, −4)
