Complex numbers
10.1 Introduction
In the previous chapter, we have shown that a single frequency wave can be represented by a phasor. We begin this chapter with a brief look at linear system theory. Such systems, when the input is a single frequency wave, produce an output at the same frequency which may be phase shifted with a scaled amplitude. Using complex numbers the system can be represented by a number which multiplies the input phasor having the effect of rotating the phasor and scaling the amplitude. We can define j as the number which rotates the phasor by π /2 without changing the amplitude. If this multiplication is repeated, hence rotating the phasor by (π/2) + (π /2) = π, then the system output will be inverted. In this way we can get the fundamental definition j2 = −1. j is clearly not a real number as any real number squared is positive. j is called an imaginary number.
The introduction of imaginary numbers allows any quadratic equation to be solved. In previous chapters we said that the equation ax2 + bx + c = 0 had no solutions when the formula leads to an attempt to take the square root of a negative number. The introduction of the number j makes square roots of negative numbers possible and in these cases the equation has complex roots. A complex number, z, has a real and imaginary part, z = x + jy where x is the real part and y is the imaginary part. Real numbers are represented by points on a number line. Complex numbers need a whole plane to represent them.
We shall look at operations involving complex numbers, the conversion between polar and Cartesian (rectangular) form and the application of complex numbers to alternating current theory.
By looking at the problem of motion in a circle, we show the equivalence between polar and exponential form of complex numbers and represent a wave in complex exponential form. We can also obtain formulae for the sine and cosine in terms of complex exponentials, and we solve complex equations zn = c, where c is a complex number.
10.2 Phasor rotation by π/2
In system theory, a system is represented (Figure 10.1) as a box with an input and an output. We think about the system after it has been in operation for a length of time, so any initial switching effects have disappeared.

Of particular importance are systems which, when the input is a single frequency wave, produce an output, at the same frequency that can be characterized by a phase shift and a change of amplitude of the wave. Examples of such systems are electrical circuits which are made up of lumped elements, that is, resistors, capacitors, and inductors. Here the input and output are voltages. Such a system is shown in Figure 10.2(a). Equivalent mechanical systems are made up of masses, springs and dampers, and the input and output is the external force applied and the tension in the spring. An example of such a mechanical system is shown in Figure 10.2(b).

We saw in Chapter 9 that a single frequency wave can be characterized by its amplitude and phase and these can be represented by vectors, called phasors. The advantage of complex numbers is that a phasor can be treated as a number and the system can be represented also by a number multiplying the input phasor.
Consider a single frequency input of 0 phase and amplitude 1. If there is a system which has the effect of simply shifting the phase by π/2, then we represent this by the imaginary number j. So j × 1∠0 = 1 ∠π /2. This system is shown in Figure 10.3(a). Supposing now we consider a system which can be broken into two components both of which shift the phase by π2![]() as shown in Figure 10.3(b). The combined effect of the two systems is to multiply the input by j × j. The final output wave, shifted now by π, is the cos(ωt + π) = – cos(ωt) so it is −1 times the initial input. For this to be so then j × j = −1.
as shown in Figure 10.3(b). The combined effect of the two systems is to multiply the input by j × j. The final output wave, shifted now by π, is the cos(ωt + π) = – cos(ωt) so it is −1 times the initial input. For this to be so then j × j = −1.

This is the central definition for complex numbers:
j?×?j?=−1
![]()
meaning that j?=?√−1![]() , where j is an operator which rotates a phasor by π /2.
, where j is an operator which rotates a phasor by π /2.
We will return to these linear time-invariant systems in Chapter 16.
10.3 Complex numbers and operations
Complex numbers allow us to find solutions to all quadratic equations. Equations like x2+ 4 = 0 do not have real roots because
x2?+?4?=?0?⇔?x2?=?−4
![]()
and there is no real number, which if squared will give −4.
If we introduce new numbers by using j?=?√−1![]() then a solution to x2 + 4 = 0 is x = j2. j2 is an imaginary number. To check that j2 is in fact a solution to x2+ 4 = 0, substitute it into the equation x2 + 4 = 0, to give
then a solution to x2 + 4 = 0 is x = j2. j2 is an imaginary number. To check that j2 is in fact a solution to x2+ 4 = 0, substitute it into the equation x2 + 4 = 0, to give
(j2)2?+?4?=?0⇔j2(2)2?+?4?=?0⇔(−1)(4)+4?=?0?using?j2?=?−1⇔0?=?0

which is true.
Therefore, x = j2 is a solution. In order to solve all possible quadratic equations we need to use complex numbers, that is numbers that have both real and imaginary parts. Mathematicians often use i instead of j to represent √−1![]() However, j is used in engineering work to avoid confusion with the symbol for the current.
However, j is used in engineering work to avoid confusion with the symbol for the current.
Real and imaginary parts and the complex plane
A complex number, z, can be written as the sum of its real and imaginary parts:
z?=?a?+?jb
![]()
where a and b are real numbers.
The real part of z is a (Re (z) a). The imaginary part of z is b(Im(z) = b).
Complex numbers can be represented in the complex plane (often called an Argand diagram) as the points (x, y) where
z?=?x?+?jy
![]()
for example, z = 1 –j2 is shown in Figure 10.4. The methods used for visualizing and adding and subtracting complex numbers is the same as that used for two-dimensional vectors in Chapter 9.

Equality of two complex numbers
Two complex numbers can only be equal if their real parts are equal and their imaginary parts are equal.
Example 10.1
If a −2 + jb = 6 + j2, where a and b are known to be real numbers, then find a and b
Solution
a?−?2?+?jb?=?6?+?j2
![]()
We know that a and b are real, so
a−2=6(real?parts?must?be?equal)⇔a=8b=2(imaginary?parts?must?be?equal)

Check by substituting a = 8 and b = 2 into
a?−?2?+?jb?=?6?+?j2
![]()
which gives
8−2?+?j2=6?+?j2⇔6?+?j2?=?6?+?j2
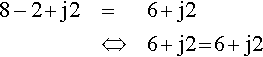
which is correct
Addition of complex numbers
To add complex numbers, add the real parts and the imaginary parts.
Example 10.2
Given z1 = 3 + j4 and z 2 = 1 –j2, find z1 + z2.
Solution
z1?+?z2?=?3?+?j4?+?1?−j2?=?(3+1)?+?j(4−2)?=?4?+j2.
![]()
On the Argand diagram, the numbers add like vectors by the parallelogram law as in Figure 10.5.

Subtraction of complex numbers
To subtract complex numbers, we subtract the real and imaginary parts.
Example 10.3
Given z1 = 3 + j4 and z2 = 1 –j2, find z1–z2.
Solution
z1?−?z2?=?3?+?j4?−?(1−j2)?=?3−1?+?j(4−(−2))?=?2?+j6.
![]()
On the Argand diagram, reverse the vector z1 to give −z2 and then add z1 and −z2 as in Figure 10.6.

Multiplication of complex numbers
To multiply complex numbers multiply out the brackets, as for any other expression, and remember that j2 = −1.
Example 10.4
Given z1 = 3 + j4 and z2 = 1 –j2, find z1 · z2.
Solution
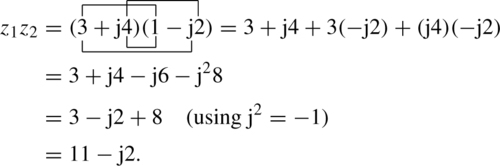
Example 10.5
Find (4 –j2)(8 – j).
Solution Multiplying as before gives
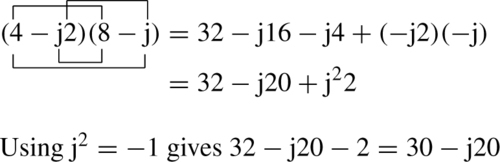
The complex conjugate
The complex conjugate of a number, z = x + jy, is the number with equal real part and the imaginary part negated. This is represented by z*:
z*?=?x?−?jy
![]()
A number multiplied by its conjugate is always real and positive (or zero). For example, z = 3 + j4 ⇔ z* = 3 –j4.
zz*=(3+j4)(3−j4)?=?(3)(3)?+?(j4)3?+?3(−j4)?+?(j4)(−j4)=9+j12?−?j12?−?j216=9−?j216?=?9?+?16=?25?(using?j2?=?−1).
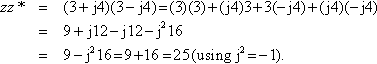
Note that the conjugate of the conjugate takes you back to the original number.
z=3+j4z*=3−j4z**=3+j4?=?z
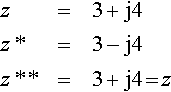
The conjugate of a number can be found on an Argand diagram by reflecting the position of the number in the real axis (see Figure 10.7).

Example 10.6
Find complex conjugates of the following and show that zz* is real and positive, or zero, in each case
(a) 2 − j5
(b) − 4 + j2
(c) − 5
(d) j6
(e) a + jb, where a and b are real.
Solution (a) The conjugate of 2 –j5 is
(2 − j5)* = 2 + j5
Hence
zz*=(2−j5)(2+j5)?=?(2)(2)+?(−j5)2?+?2(j5)+?(−j5)(j5)=4−j10?+?j10?−j225=4?−?j225?(using?j2?=?−1)=4+25?=?29
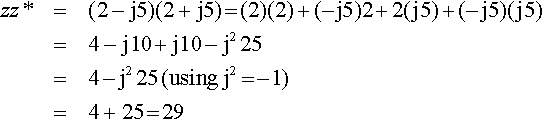
which is real and positive. We have shown that 2 – j5 multiplied by its conjugate 2 + j5 gives a real, positive number.
(b)
(−4?+?j2)*=−4−j2(−4?+j2)(−4−j2)=(−4)(−4)?+?(j2)?(−4)+?(−4)(−2)+?(j2)(−j2)=16−j8?+j8?−j24=16−j24?(using?j2?=−1)=16+4?=?20
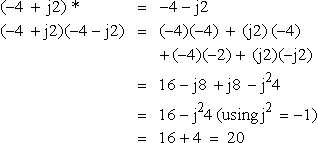
which is real and positive.
(c) −5 is a real number and therefore its complex conjugate is the same: −5. (–5)* = −5 and (–5)(–5) = 25, which is real and positive.
(d)??(j6)*=-j6(j6)(-j6)=-j236?=?36
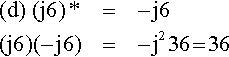
which is real and positive.
(e)
(a?+?jb)*?=a−jb(a?+?jb)(a?−?jb)=(a)(a)+(jb)(a)+?(a)(−jb)+(jb)(−jb)=a2?+?jab?−?jab?−?j2b2?=?a2?−j2b2using?j2=−1,?this?gives?a2?+?b2
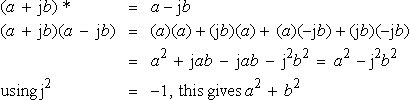
As a and b are real, this must be a real number. Also, we know that the square of a real number is greater than or equal to 0. So a2 + b2 is real, and it is positive if a ≠ 0, b ≠ 0 or zero if both a and b are zero.
It is a good idea to remember this last result that a + jb multiplied by its conjugate, a – jb, gives a2 + b2. That is, any number multiplied by its complex conjugate gives the sum of the square of the real part and the square of the imaginary part. This is the same as the value of the modulus of z squared, that is,
zz*?=?|z|2.
![]()
Division of complex numbers
To divide complex numbers, we use the fact that a number times its conjugate is real to transform the bottom line of the fraction to a real number. If we multiply the bottom line by its complex conjugate, we must also multiply the top line in order not to change the value of the number.
Example 10.7
Given z1 = 3 + j4 and z2= 1 – j2, find z1/ z2.
Solution
z1z2=3+j41−?j2=(3+j4)(1+j2)(1−j2)(1+j2)

Here, we have multiplied the top and bottom line by z*2 to make the bottom line entirely real. Hence, we get
(3+j4?+?j6?+j28)(1+22)?=?(−5?+?j10)5?=?−55?+?j105?=?−1+j2.
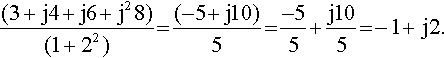
Example 10.8
Find
−3?+?j210+?j5

in the form x + jy.
Solution Multiply the top and bottom line by the complex conjugate of 10 + j5 to make the bottom line real
−3?+?j210+?j5=(−3+j2)(10−j5)(10?+?j5)?(10−j5)=(−3)(10)+j2(10)+(−3)(−j5)+(j2)(−j5)(102−52)=−30?+?j20?+?j15?−?j210125=−30?+?j20?+?j15?−?10125=−20?+?j35125?=?−20125?+?j35125?=?−0.16+?j0.28.

10.4 Solution of quadratic equations
In Chapter 2 of the Background Mathematics Notes available on the companion website for this book, we looked at solutions of ax2 + bx + c = 0 where a, b and c are real numbers and said that the solutions are given by the formula
x?=?−b?±√b2?−?4ac2a

We discovered that there are no real solutions if b2 –4ac < 0 because we would need to take the square root of a negative number. We can now find complex solutions in this case by using j?=?√−1![]() .
.
Example 10.9
Solve the following where x ε ![]() , the set of complex numbers:
, the set of complex numbers:
(a) x2 + 3x + 5 = 0
(b) x2 – x + 1 = 0
(c) 4x2 – 2x + 1 = 0
(d) 4x2 + 1 = 0
Solution (a) To solve x2+3x+5 = 0, compare with ax2 + bx + c = 0.
This gives a = 1, b = 3, and c = 5. Substitute in
x?=?−b?±?√b2−4ac2a
![]()
to give
x?=?−3?±?√32−4(1)(5)2(1)?=?−3?±?√−112

We write −11 = (–1) · (11), so
√−11?=?√−1√11?≈?j3.317???(using?j?=?√−1)
![]()
Therefore,
x?≈?−3?±?j3.3172?⇒?x?≈?−?1.5?+?j1.658?∨?x?≈?1.5?−?j1.658.

(b) To solve x2 – x + 1 = 0, compare it with ax2 + bx + c = 0. We all that a = 1, b = −1, and c = 1. Substitute in
x?=?−b?±?√b2−4ac2a

to give
x?=?−(−1)?±?√(−1)2−4(1)(1)2(1)?=?+1?±?√−32

We write −3 = (–1) ·3, so
√−3?=?√−1√3?≈?j1.732????(using?j?=?√−1)
![]()
Therefore,
x?≈?1?±?j1.7322?⇒?x?≈?0.5?+?j0.866?∨x?≈?0.5?−?j0.866.

(c) To solve 4x2 – 2x + 1 = 0, compare it with ax2+ bx + c = 0. We get a = 4, b = −2, and c = 1. Substitute in
x?=?−b?±?√b2−4ac2a

to give
x?=?−(−2)?±?√(−2)2−4(4)(1)2(4)?=?2?±?√−128

We write −12 = (–1) ·12, so
√−12?=?√−1√12?≈?j3.4641?(using?j?=?√−1)
![]()
Therefore,
x?≈?2?±?j3.46418?⇔?x?≈?0.25?+?j0.433?∨?x?≈0.25?−?j0.433.

(d) To solve 4x2 + 1 = 0, we could use the formula as in the other cases but it is quicker to do the following:
4x2?+?1?⇔4x2?=?−1??(subtracting?1?from?both?sides)⇔x2?=?−14?(dividing?both?sides?by?4)⇔x?=?±?√−0.25???(taking?the?square?root?of?both?sides)

as √−0.25?=?√−1?√0.25?=?j0.5![]() , we get x = ±j0.5 ⇔ x = j0.5 ∨ x = −j0.5.
, we get x = ±j0.5 ⇔ x = j0.5 ∨ x = −j0.5.
If ax2 + bx + c = 0 and the coefficients a, b, c are all real numbers, then we find that the two roots of the equation, if they are not entirely real, must be the complex conjugates of each other. This is true for all the cases we looked at in Example 10.9.
x2?+?3x?+?5?=0
![]()
has solutions x = −1.5 + j 1.658 and x = −1.5 − j 1.658.
x2?−?x?+?1?=0
![]()
has solutions x = 0.5 + j0.866 and x = 0.5 – j0.866.
4x2?+?1?=0
![]()
has solutions x = j0.5 and x = −j0.5.
We can show that if the coefficients a, b, and c are real in the equation ax2 + bx + c = 0, then the roots of the equation must either be real or complex conjugates of each other. We know from the formula that
ax2?+bx?+c?=0?⇔?x?=?−b?±?√b2−4ac2a

If x has an imaginary part, then b2– 4ac < 0, so that √b2?−?4ac![]() is an imaginary number. We can write this is terms of j as follows:
is an imaginary number. We can write this is terms of j as follows:
√b2?−?4ac?=?√−?(4ac−b2)?=?√−1√(4ac−?b2)?=?j√(4ac−?b2)
![]()
So the solutions, in the case, b2–4ac < 0 are
x?=?−b?±?j√4ac−b22a

which can be written, using
p?=?−b2a
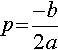
and
q?=?√4ac−?b22a,
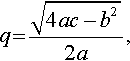
as
x?=?p?±?jq?⇔?x?=?p?−?jq?∨?x?=?p?+?jq
![]()
where p and q are real.
This shows that the two solutions are complex conjugates of each other. This fact can be used to find the other root when one root is known.
Example 10.10
Given that the equation x2 –kx + 8 = 0, where k ε ![]() has one solution x = 2 – j2 then find the other solution and also the value of k.
has one solution x = 2 – j2 then find the other solution and also the value of k.
Solution We know that non-real solutions must be complex conjugates of each other so if one solution is x = 2 –j2 the other one must be x = 2 + j2. To find k, we use the result that if an equation has exactly two solutions xl and x2, then the equation must be equivalent to (x –x1)(x – x2) = 0. We know that x = 2 + j2 or x = 2 – j2, therefore, the equation must be equivalent to
(x−?(2+j2))(x−(2−j2))?=?0
![]()
Multiplying out the brackets gives:
x2−x?(2+j2)?−?x(2−j2)+(2+j2)(2−j2)?=?0⇔?x2+?x(−2−j2?−2?+j2)?+?(4+4)?=?0⇔?x2?−?4x?+?8?=?0

Compare x2 – 4x + 8 = 0 with x2 – kx + 8 = 0. The coefficient of x2 are equal in both cases, as are the constant terms, so the equations would be the same if –k = −4 ⇔ k = 4, giving the solution as k = 4.
10.5 Polar form of a complex number
From the Argand diagram in Figure 10.8, we can see that a complex number can be expressed in terms of the length of the vector (the modulus) and the angle it makes with the x-axis (the argument). This is exactly the same process as that as in expressing vectors in polar coordinates as in Section 9.4.
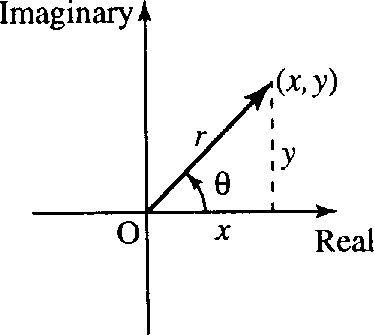
If z = x + jy then z can be represented in polar form as r ∠ θ where
r2?=?x2?+?y2
![]()
tan?(θ)?=?yx
![]()
Hence
r?=?√x2?+?y2,???θ?=?tan−1?(yx)???(+?π?if?x?is?negative)

We can write the complex number as
z=?r?∠θ
![]()
r, the modulus of z, is also written as |z|.
As it is usual to give the angle between –π and π, it may be necessary to subtract 2π from the angle given by this formula. As 2π is a complete rotation, this will make no difference to the position of the complex number on the diagram.
Example 10.11
Express the following complex numbers in polar form
(a) 3 + j2
(b) − 2 − j5
(c) − 4 + j2
(d) 4 − j2
Solution To perform these conversions to polar form, it is a good idea to draw a diagram of the number in order to check that the angle is of the correct size (see Figure 10.9).

(a) 3 + j2 has modulus r?=?√32?+?22?≈?3.61![]() and the angle is given by tan−l (2/3); therefore, in polar form 3 + j2 ≈ 3.61∠0.59
and the angle is given by tan−l (2/3); therefore, in polar form 3 + j2 ≈ 3.61∠0.59
(b) –2 – j5 has modulus r?=?√(−2)2?+?(−5)2?≈?5.39![]() and the angle is given by tan−1 (–5/ (–2)) +π ≈ 4.332. As this angle is bigger than 2π, subtract 2π (a complete revolution) to give −1.95. Therefore, in polar form −2 – j5 ≈ 5.39∠–1.95. Note that the angle is between –π and –π /2, meaning that the number must lie in the third quadrant, which we can see is correct from the diagram.
and the angle is given by tan−1 (–5/ (–2)) +π ≈ 4.332. As this angle is bigger than 2π, subtract 2π (a complete revolution) to give −1.95. Therefore, in polar form −2 – j5 ≈ 5.39∠–1.95. Note that the angle is between –π and –π /2, meaning that the number must lie in the third quadrant, which we can see is correct from the diagram.
(c) –4 + j2 has modulus r?=?√(−4)2?+?22?≈?4.47![]() and the angle is given by tan−l (2/(–4)) + π ≈ −0.46 + π ≈ 2.68. Therefore, in polar form −4+j2 ≈ 4.47 ∠2.68. Note that the angle is between π/2and π, meaning that the number must lie in the second quadrant, which we can see is correct from the diagram.
and the angle is given by tan−l (2/(–4)) + π ≈ −0.46 + π ≈ 2.68. Therefore, in polar form −4+j2 ≈ 4.47 ∠2.68. Note that the angle is between π/2and π, meaning that the number must lie in the second quadrant, which we can see is correct from the diagram.
(d) 4 – j2 has modulus r?=?√(4)2?+(−?2)2?≈?4.47![]() and the angle is given by tan−1 (–2/4) ≈ −0.46. Therefore, in polar form 4 – j2 ≈ 4.47∠– 0.46. Note that the angle is between –π /2 and 0 meaning that the number must lie in the fourth quadrant, which we can see is correct from the diagram.
and the angle is given by tan−1 (–2/4) ≈ −0.46. Therefore, in polar form 4 – j2 ≈ 4.47∠– 0.46. Note that the angle is between –π /2 and 0 meaning that the number must lie in the fourth quadrant, which we can see is correct from the diagram.
Check the calculations by using the rectangular to polar conversion facility on your calculator.
Conversion from polar form to Cartesian (rectangular) form
If a number is given by its modulus and argument, in polar form, r ∠θ, we can convert back to Cartesian (rectangular) form using:
x = r cos(θ) and y = r sin(θ) This can be seen from Figure 10.10 and examples are given in Figure 10.11. As z = x + jy, z = r cos(θ) + jr sin(θ) = r(cos(θ) + j sin(θ)).


Addition, subtraction, multiplication, and division of complex numbers in polar form
To add and subtract two complex numbers, always express them first in rectangular form; that is, write as z = a + jb. The result of the addition or subtraction then can be converted back to polar form.
To multiply two numbers in polar form, multiply the moduli and add the arguments.
To divide two numbers in polar form divide the moduli and subtract the arguments.
Example 10.12
Given
z1?=?3∠π/6???z2=?2?∠π/4
![]()
Find zl + z2, zl –z2, zlz2, and zl/z2.
Solution To find zl + z2 use r ∠θ = r(cos(θ) + j sin(θ))
z1=3(cos(π/6)?+?j?sin(π/6))?≈?2.5981?+?j?1.5z2=2(cos(π/4)?+?jsin?(π/4))?≈?1.4142+??j1.4142z1?+?z2≈2.5981?+j1.5?+?1.4142?+?j1.4142=4.0123?+?j2.9142.

To express zl + z2, back in polar form, use r?=?√x2?+?y2![]() and θ = tan−1(y /x) (+π if x is negative).
and θ = tan−1(y /x) (+π if x is negative).
r=√4.01232?+?2.91422≈?4.959,θ=tan−1(2.9142/4.0123)?≈?0.6282
![]()
Hence, zl + z2 ≈ 4.959∠0.6282.
To find zl – z2 we already have found (above) that zl = 3∠π/6 ≈ 2.5981 + j1.5 and z2 = 2∠π/4 ≈ 1.4142 + j1.4142. So zl – z2 ≈ 2.5981 + j1.5– (1.4142 + j1.4142) = 1.1839 + j0.0858.
To express zl–z2 back in polar form use, r?=?√x2?+?y2![]() and θ = tan−1(y / x) (+π if x is negative).
and θ = tan−1(y / x) (+π if x is negative).
Then zl – z2 ≈ 1.1839 + j0.0858 ≈ 1.187 ∠0.0723.
To find zl z2, multiply the moduli and add the arguments:
z1z2?=?3∠π/6?⋅?2∠π/4?=?(3)?⋅?(2)∠((π/6)?+?(π/4))?=?6∠5π/12.
![]()
To find zl/z2, divide the moduli and subtract the arguments:
z1z2?=?3∠π/62∠π/4?=?32∠((π/6)−(π/4))?=?1.5∠−π/12.

10.6 Applications of complex numbers to AC linear circuits
An alternating current (AC) electrical circuit consisting of resistors, capacitors, and inductors can be analysed using the relationship
V?=?ZI
![]()
where V is the voltage, Z the impedance, and I the current and V, Z, and I are all complex quantities.
Each component has a complex impedance associated with it and for two components in series, as in Figure 10.12(a), the resultant impedance ZR is found by the formula
ZR?=?Z1?+?Z2
![]()
For two components in parallel, as in Figure 10.12(b), the resultant impedance is given by
1ZR?=?1Z1?+?1Z2


In the case of parallel circuit elements, it may be easier to calculate the admittance, the reciprocal of the impedance Y = 1/ Z. Then use the fact that for circuit elements in parallel
YR?=?Y1?+?Y2?and?V?=?I/Y.
![]()
The real part of Z is called the resistance and the imaginary part is called the reactance.
Z?=?R?+?jS
![]()
where R is the resistance in ohms and S is the reactance in ohms.
The impedances of circuit elements are as follows:
| Resistor | Z = R | No reactive element |
| Capacitor | Z = 1/(jωC) = −j/(ωC) | Purely reactive |
| Inductor | Z = jωL | Purely reactive |
where ω is the angular frequency of the source, ω = 2π f, f is the frequency in Hz, R is the resistance (in ohms), C is the capacitance (in farads), and L is the impedance (in henries).
Example 10.13
Find the impedance of the circuit shown in Figure 10.13(a) at 20kHz where L = 2mH, C = 100 μF, and R = 2000Ω. Assuming a voltage amplitude of 300 V, calculate the current I and relative phase.

Solution The impedances of the elements are shown in Figure 10.13(b). As we are given that f, the frequency of the input, is 20 kHz, ω = 2π f = 2π × 20 × 103. As the elements are in series, we can sum the impedances
Z=R?+?jωL?−?jωC=2000?+?j2π?×?20?×?103?×?2×?10−3−?j2π?×?20?×?103?×?100?×?10−6

giving
2000?+?j?(80−14π)?≈?2000?+?j251.2
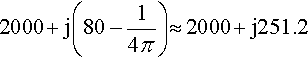
Expressing this is polar form gives Z ≈ 2016∠7°. Therefore, from V =ZI and given V = 300,
I?=?300Z?=?3002016∠7°?≈?0.149∠?−?7°.
![]()
giving a current of magnitude 0.149 A with a relative phase of −7°.
Example 10.14
One form of a ‘tuned circuit’ that can be used as a band-pass filter is given in Figure 10.14(a). Given that R = 300 Ω, L = 2 mH, and C = 10 μF, find the admittance of the circuit at 2 kHz. Given that the current source is of amplitude 12 A, find the voltage amplitude and its relative phase.
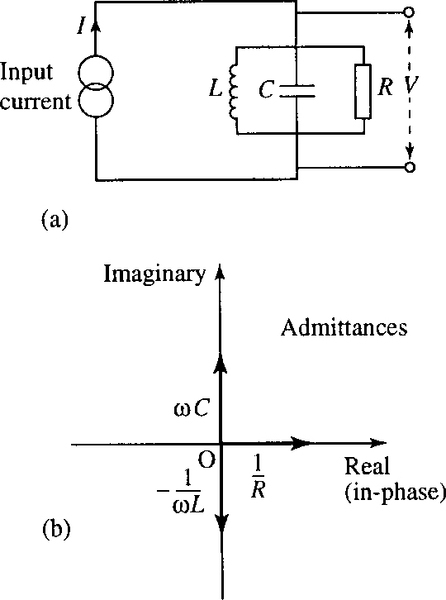
Solution The admittances of the elements are shown in Figure 10.14(b). As the elements are in parallel, we can sum the admittances
Y?=1R?+jωC?−jωL???where?ω?=?2?×?103?×?2?π

giving
Y=1300?+?j(2π?×?103?×?2?×?10?×?10−6)−?j2?×?103?×?2π?×?2?×?10−3≈0.003333?+?j0.0859.
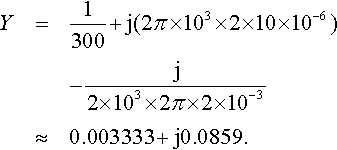
Expressing this is polar form gives Y = 0.086∠88°. Therefore, from V = ZI or V = I / Y, we have
V?=?120.086∠88°?≈?139.6?∠?−?88°
![]()
giving a voltage amplitude of 139.6 V with a relative phase of −88°.
10.7 Circular motion
When we introduced the sine and cosine function in Chapter 5, we used the example of a rotating rod of length r. We plotted the position of the rod, its height, and horizontal distance from the centre against the angle through which the rod had rotated. This defined the sine and cosine functions. We consider this problem again. This time we specify that the circular motion is at constant angular velocity ω. That is, the rate of change of the angle θ, dθ/ dt, is constant and equals ω. That is:
dθdt?=ω???(where?ω?is?a?constant)

⇔???θ?=?ωt?+?ϕ
![]()
where φ is the angle when t = 0. If we start with the rod horizontal, then φ = 0 and we have θ = ωt, The (x, y) position of the tip of the rod of length r is given as a function of time by x = r cos (ωt) and y = r sin (ωt), where ω is the constant angular velocity, so the rotating vector is given by r?=?(r?cos(ωt),??r?sin(ωt))??with?θ?=?ωt.![]()
Consider now a ball on the end of a string with constant angular velocity ω. Can we obtain an expression for its acceleration? The acceleration is of particular importance because we know from Newton's second law that the force required to maintain the circular motion can be found by using F = ma, where F is the force, m is the mass, and a is the acceleration. We assume, in this discussion, that the effects of gravity and air resistance are negligible. The ball is being rotated in a plane which is vertical to the ground.
First, imagine lying flat on the ground in a line with the x-axis and watching the ball. It appears to oscillate back and forth and its position is given by x = r cos(ωt). This is pictured in Figure 10.15.
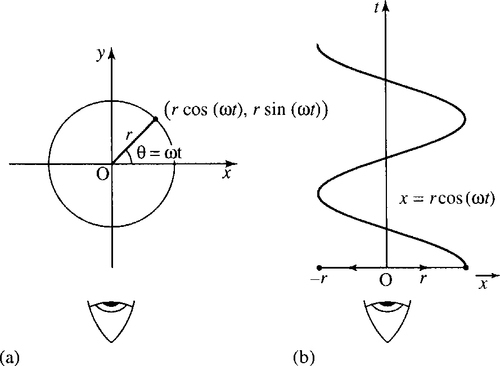
Differentiating with respect to t gives the component of the velocity in the x-direction
dxdt?=?−?rω?sin?(ωt).
![]()
The acceleration is the derivative of this velocity
ddt(dxdt).

This is also written as d2x /dt2(read as ‘d two x by dt squared’) and it means the derivative of the derivative
dxdt?=?−?rω?sin?(ωt)
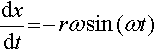
differentiating again gives
d2xdt2?=?−?rω2?cos?(ωt)?=?−ω2?(r?cos?(ωt))

and as x = r cos(ωt)
d2xdt2?=?−ω2x.
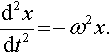
This equation tells us that the horizontal acceleration is proportional to the horizontal distance from the origin in a direction towards the origin. This type of behaviour is called simple harmonic motion.
We can consider the movement in the y-direction by changing our point of view as in Figure 10.16. Again we can find the component of the acceleration, this time in the y-direction.
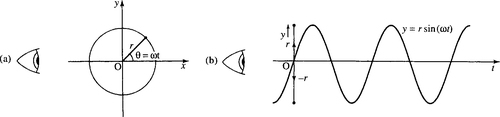
We differentiate y = r sin(ωt) to get the component of velocity in the y-direction:
dydt?=?rω?cos?(ωt)

Differentiate again to find the acceleration:
d2ydt2?=?-rω2?sin?(ωt)

and as y = r sin(ωt)
d2ydt2?=?−ω2y
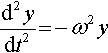
Notice that this is the same equation as we had for x. We can represent the motion, both in the x- and y-directions by using a complex number to represent the rotating vector. The real part of z represents the position in the x-direction and the imaginary part of z represents the position in the y-direction:
z?=?x?+?jy?=?r?cos?(ωt)?+?jr?sin(ωt)
![]()
Then
dzdt?=?−rω?sin(ωt)?+?jr?ω?cos(ωt)

The real part of dz / dt represents the component of velocity in the x-direction and the imaginary part represents the velocity in the y-direction. Again, we can differentiate to find the acceleration
d2zdt2?=−rω2?cos(ωt)?−?jr?ω2?sin(ωt)=−ω2?(rcos(ωt)?+?jr?sin(ωt))?=?−?ω2z
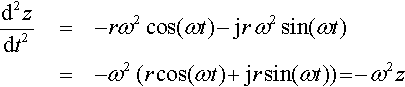
as
z?=?r?cos(ωt)?+?jr?sin?(ωt)
![]()
So, we get
d2zdt2?=?−?ω2z

This shows that the acceleration operates along the length of the vector z towards the origin and it must be of magnitude |–ω2 z| = ω2r where r is the radius of the circle. The ball is always accelerating towards the centre of the circle. This also tells us the force that the string must provide in order to maintain the circular motion at constant angular velocity. The force towards the centre, called the centripetal force, must be | F| = mω2r, where r is the radius of the circle and m is the mass of the ball. This has been given by Newton's second law F = ma.
We can use the equation for circular motion to show that it is possible to represent a complex number, z, in the form z = r ejθ, where r is the modulus and the argument. To do this we must first establish the conditions which determine a particular solution to the equation
d2zdt2?=?−?ω2z

We know that one solution of the differential equation
d2zdt2?=?−?ω2z
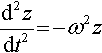
with the condition that z = r when t = 0, is given by z = r cos(ωt) + jr sin(ωt). Unfortunately, there is at least one other solution, given by the case where the string travels clockwise rather than anti-clockwise, that is, z = r cos(–ωt) +jr sin –ωt). However, we can pin down the solution to the anti-clockwise direction of rotation by using the fact that we defined the angular velocity by dθ/dt = ω. This gives a condition on the initial velocity (at t = 0). From Figure 10.17 we can see that the velocity must be positive and only have a component in the y-direction at t = 0.

This discounts the possibility of the motion being clockwise as this would give a negative initial velocity. From z = r cos(ωt) + jr sin(ωt)
dzdt?=?−rω?sin(ωt)?+?jr?ω?cos(ωt)dt
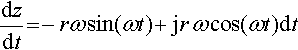
and at t = 0, dz/dt = jrω. We now have enough information to say that
d2zdt2?=?−?ω2z?and?z?=?r?when?t=?0

and
dzdt?=?−jωr??when??t=0???⇔???z?=?r?cos(ωt)?+?jrsin(ωt)
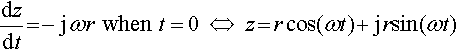
In Chapter 8 we looked at the exponential function and we found that y = y0 ekt is a solution to the equation d y/dt = ky. This equation models the situation where the rate of change of the population is proportional to its current size: the first derivative of y is proportional to y. The equation
d2zdt2?=?−?ω2z
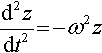
is similar only now the acceleration is related to z, that is the second derivative is proportional to z. As the exponential functions have the property that the derivative gives a scaled version of the original function, we must also get a scaled version of the original function if we differentiate twice. So we can try a solution of the form z = r ekt for the equation
d2zdt2=−?ω2zz=r?ekt⇒dzdt?=?rk?ekt⇒d2zdt2?=?rk2?ekt

Substituting into
d2zdt2?=?−?ω2z

we get
rk2?ekt?=?−?ω2r?ekt
![]()
Dividing both sides by r ekt gives k2= –ω2⇔ k = ±jω.
This gives two possible solutions: z = r ejωtwhen k = jω and z = r e−jωtwhen k = –jω. Again, we can use the initial velocity to determine the solution. Using z = r ejωtwe get
dzdt?=?jrω?ejωt

at t = 0 then we get the velocity as jωr, which was one of the conditions we wanted to fulfil.
This shows that the two expression z = r ejωt and z = r cos (ωt) + jr sin(ωt) both satisfy
d2zdt2?=?−ω2z??and?z?=?r???when?t?=?0
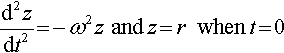
and
dzdt?=?jωr???when?t?=?0.
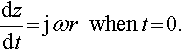
We have stated that these initial conditions are enough to determine the solution of the differential equation. So, the only possibility is that
r?ejωt?=?r?cos(ωt)?+?jr?sin?(ωt)
![]()
This shows the equivalence of the polar form of a complex number and the exponential form. Replacing ωt by θ, we get r ejθ = r cost(θ) + jr sin (θ), which we recognize as the polar form for a complex number z = r ∠θ where r is the modulus and θ is the argument. We can represent any complex number z = x + jy in the form r ejθ. r and θ are found, as given before for the polar form, by
r?=?√x2?+?y2
![]()
θ?=?tan?−1(yx)??(+?π?if?x?is?negative)

Conversely, to express a number given in exponential form in rectangular (Cartesian) form, we can use r ejθ = r cos(θ) + jr sin (θ).
Example 10.15
Show that z = 2 ej3t is a solution to d2z/dt2 = –9z where z = 2 when t = 0 and dz/dt = j6 when t = 0.
Solution If z = 2 ej3t, then when t = 0, z = 2 e0 = 2
dzdt?=?2?(j3)ej3t?=?j6ej3t

when t = 0
dzdt?=?j6e0?=?j6.
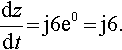
Hence
d2zdt2=j6(j3)?ej3t⇒?d2zdt2?=?−?18ej3t

Substituting into d2z/dt2= –9z gives −18 ej3t= −9(2 ej3t) ⇔ –18 ej3t= −18 ej3t, which is true.
Example 10.16
Express z = 3 + j4 in exponential form.
Solution The modulus r if given by
r?=?√32?+?42?=?√25?=?5
![]()
The argument is tan−1 (4/3) ≈ 0.9273. Hence, z ≈ 5 ej0.9273.
Example 10.17
Find the real and imaginary parts of the following
(a) 3 ej(π/2)
(b) e−j
(c) e3+j2
(d) e−j(j−1)
(e) jj
Solution (a) Use r ejθ= r cos(θ) + jr sin(θ) ·3 ej(π/2) has r = 3 and θ = π /2
3?ej(π/2)=3?cos(π/2)?+?j3?sin(π/2)=3.0?+?j(3)(1)?=?j3

The real part is 0 and the imaginary part is 3.
(b) Comparing e−jwith rejθ gives r = 1 and θ = −1. Using r ejθ= r cos(θ) + jr sin(θ)
e−j=1?cos(−1)?+?j?sin(−1)≈0.5403?−?j0.8415
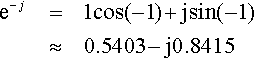
So the real part of e−jis approximately 0.5403 and the imaginary part is approximately −0.8415.
(c) Notice that e3+j2 is not in the form r ejθbecause the exponent has a real part. We therefore split the exponent into its real and imaginary bits by using the rules of powers:
e3+j2?=?e3?ej2
![]()
e3 ≈ 20.09 is a real number, and the remaining exponent j2 is purely imaginary:
e3ej2?≈?20.09ej2
![]()
Comparing e3ej2 with rejθ gives r = e3 and θ = 2. Using rejθ = r cos(θ) + jr sin(θ) gives
e3?ej2?=?e3?cos(2)?+je3?sin?(2)≈?−?8.359?+?j?18.26

The real part of e3+j2 is approximately −8.359 and the imaginary part is approximately 18.26.
(d) For e−j(j–1) we need first to write the exponent in a form that allows us to split it into its real and imaginary bits. So, we remove the brackets to give
e−j(j−1)?=?e−j2+j
![]()
Using j2 = −1, this gives
e−j(j−1)?=?e1+j
![]()
Now, using the rules of powers we can write
e1+j = e1ej. e1 is a real number and the exponent of ej is purely imaginary. Comparing e1ej with rejθgives r = e1 and θ = 1. Using rejθ = r cos(θ) + jr sin(θ) gives
e1?ej1?=?e1?cos?(1)?+?je1?sin(1)≈?1.469?+?j2.287

The real part of e−j(j–1) is approximately 1.469 and the imaginary part is approximately 2.287
(e) jj looks a very confusing number as we have only dealt with complex powers when the base is e. We therefore begin by looking for a way of rewriting the expression so that its base is e. To do this, we write the base, j, in exponential form. From the Argand diagram in Figure 10.18, as j is represented by the point (0,1) we can see that that it has modulus 1 and argument π /2. Hence, j = ej(π/2).

Use this to replace the base in the expression jj so that
jj = (ej(π/2))j = ej2(π/2) = e−π/2. We can now see that jj is in fact a real number!
jj?=?e−π/2?≈?0.2079.
![]()
The real part of jj is approximately 0.2079 and the imaginary part is 0.
10.8 The importance of being exponential
We have shown that
r?ejθ?=?r?cos(θ)?jr?sin(θ)?=?r∠θ
![]()
Here r is the modulus of the complex number and θ is the argument. Therefore, the exponential form is simply another way of writing the polar form. The advantage of the exponential form is its simplicity. For circular motion, at constant angular velocity, it can represent the motion both in the real and imaginary (x and y) directions in one simple expression r ejωt. The rules for multiplication and powers of complex numbers in exponential form are given by the rules of powers, as for any other number, given in Chapter 4 of the Background Notes in Mathematics available on the companion website for this book, thus confirming the rules that we gave for the polar form.
Multiplication:
r1?ejθ1?r2?ejθ2?=?r1?r2ej(θ1?+?θ2)
![]()
That is, we multiply the moduli and add the arguments.
Division:
r1?ejθ1r2?ejθ2?=?r1r2e(θ1−θ2)

That is, we divide the moduli and subtract the arguments.
The complex conjugate is of a number r ejθ is the number of same modulus and negative argument. That is, the complex conjugate of r ejθis r e−jθ
Powers:
(r?ejθ)n?=?r?ejnθ.
![]()
That is, to raise a complex number to the power n, take the nth power of its modulus and multiply its argument by n.
Example 10.18
Given z1 = 3 j(π/6)z2 = 2 ej(π/4), Find zl + z2, zl – z2, zlz2, zl/z2, z*1z*2 and z31![]()
Solution To find zl + z2, use r ejθ= r(cos(θ) + j sin(θ))
z1?=?3?ej(π/6)?=?3(cos(π6)?+?j?sin(π6))?≈?2.5981?+?j1.5z2?=?2?ej(π/4)?=?2(cos(π4)?+?j?sin(π4))?≈?4.4142?+?j1.4142

Therefore,
z1?+?z2?≈?2.5981?+?j?1.5?+?1.4142?+?j1.4142?=?4.0123?+?j2.9142
![]()
To express z1 + z2 back in exponential form, use r?=?√x2?+?y2![]() and θ = tan−1(y / x) (+π if x is negative).
and θ = tan−1(y / x) (+π if x is negative).
r?=?√(4.0123)2?+?(2.9142)2?≈?4.959?andθ?=?tan−1?(2.9142/4.0123)?≈?0.6282
![]()
Hence, z1 + z2 ≈ 4.959 ej0.6282
To find zl– z2, we already have found (above) that
z1?=?3ej(π/6)?≈?2.5981?+?j1.5??andz2?=?2ej(π/4)?≈?1.4142?+?j1.4142

Therefore
z1?−?z2?≈?2.5981?+?j1.5?−?(1.4142?+?j1.4142)?=?1.839?+?j0.0858
![]()
To express zl – z 2 back in polar form, use r?=?√x2?+?y2![]() and θ = tan−1(y /x) (+π if x is negative):
and θ = tan−1(y /x) (+π if x is negative):
z1−?z2?≈?1.1839?+?j0.0858?≈?1.187?ej0.0723.
![]()
To find z1z2, multiply the moduli and add the arguments
z1z2?=?3ej(π/6)?2ej(π/4)?=?3.2?ej(π/6)+(π/4)?=?6e−j(5π/12).
![]()
To find zl/ z2, divide the moduli and subtract the arguments
z1z2?=?3ej(π/6)2ej(π/4)?=?32?ej((π/6)−(π/4))?=?1.5?e−j(π/12).

To find z*1z*2, we find the complex conjugate of zl and z2
z*1=(3?e−j(π/6))*?=?3?ej(π/6)z*2=(2?ej(π/4))*?=?2?e−j(π/4)z*1z*2=3?e−j(π/6)2e−j(π/4)?=?3.2?e−j((π/6)+(π/4))=?6?e−j(5π/12).

To find z31![]()
z31?=?(3ej(π/6))3?=?33(ej(π/6))3?=?27ej(π/6)×?3?=?27ej(π/2).
![]()
Expressions for the trigonometric functions
From the exponential form, we can find expressions for the cosine or sine in terms of complex numbers. We begin with a complex number z of modulus 1 and its complex conjugate
ejθ?=?cos(θ)?+j?sin?(θ)
e−jθ?=?cos(θ)?−?j?sin?(θ)
From these, we can find the expression for the cosine and sine in terms of the complex exponential. Adding Equation (10.1) and (10.2), we have
ejθ?+e−jθ?=?cos(θ)?+?j?sin?(θ)?+?cos(θ)?−?j?sin(θ)??????⇔???ejθ+?e−jθ?=?2?cos(θ)

Dividing both sides by 2 gives
12(ejθ+?e−jθ)?=?cos(θ)???⇔??cos(θ)?=?12?(ejθ+?e−jθ)
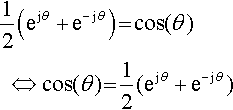
Now, subtracting Equation (10.2) from Equation (10.1), we get
ejθ−?e−jθ?=?cos(θ)?+?j?sin(θ)?−?(cos(θ)?−?j?sin(θ))???⇔?ejθ−?e−jθ?=2j?sin(θ)

Dividing both sides by 2j gives
12j(ejθ−?e−jθ)?=?sin(θ)???⇔?sin(θ)=12j(ejθ?−?e−jθ)
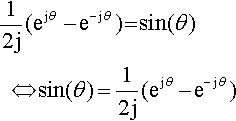
So, we have
cos(θ)?=?12(ejθ?+?e−jθ)sin(θ)?=?12j(ejθ?−?e−jθ)

Using tan(θ) = sin(θ) / cos(θ), we get
tan?(θ)?=?(1/2j)(ejθ?−?e−jθ)(1/2)(ejθ?+?e−jθ)=?1j?(ejθ?−?e−jθejθ?+?e−jθ)
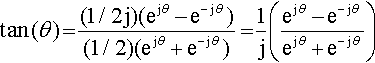
Compare these with the definition of the sinh, cosh, and tanh functions given in Chapter 8:
cosh(θ)?=?12(eθ?+?e−θ)sinh(θ)?=?12(eθ?−?e−θ)tanh(x)?=?eθ?−?e−θeθ?+?e−θ

We see that:
cos(jθ)?=cosh(θ)sin(jθ)?=j?sinh(θ)tan(jθ)?=j?tanh(θ)

De Moivre's theorem
Using the expression for the cmoplex number in terms of a sine and cosine, rejθ= r(cos(θ) + j sin(θ)), and using this in r ejθn= r ejnθ, we get
(r?(cos(θ))?+?j?sin(θ))?n?=?rn?(cos(nθ)?+?j?sin(nθ))
![]()
This is called De Moivre's theorem and can be used to obtain multiple angle formulae.
Example 10.19
Find sin(3θ) in terms of powers of sin(θ) and cos(θ).
Solution We use the fact that sin(3θ) = Im(cos(3θ)+j sin(3θ)), where Im() represents ‘the imaginary part of’. Hence
sin(3θ)?=Im(ej3θ)=Im((cos(θ)?+?j?sin(θ))3).

Expanding
(cos(θ)?+?j?sin(θ))3?=?(cos(θ)?+?j?sin(θ))(cos(θ)+?j?sin(θ))2=?(cos(θ)?+?j?sin(θ))?cos2(θ)?+?2j?cos(θ)?sin(θ)?+?j2?sin2(θ))=?cos3(θ)?+?j?sin(θ))?cos2(θ)?+?2j?cos2(θ)?sin(θ)+j2?cos(θ)?sin2(θ)?+?2j2cos(θ)?+?sin2(θ)?+?j3?sin3(θ)=?cos3(θ)?−?3j?sin(θ)?cos2(θ)?−?3cos(θ)?sin2(θ)−j?sin3(θ)=?cos3(θ)?−?3?cos(θ)?sin2(θ)?+?j(3sin(θ)?cos2(θ)?+?sin3(θ)).
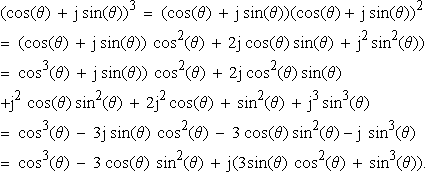
As sin(3θ) = Im((cos(θ) + j sin(θ))3), we take the imaginary part of the expression we have found to get
sin(3θ)?=?3?sin?(θ)?cos2(θ)?−?sin3(θ).
![]()
Example 10.20
Express cos3 (θ) in terms of cosines of multiples of θ.
Solution Using cos(θ) = (1/2)(ejθ+e−jθ) and the expansion (a+b)3 = a3 + 3a2b + 3ab2 + b3:
cos3(θ)=(12(ejθ?+?e−jθ))3=123(ej3θ?+3ejθ?+?3e−jθ?+e−j3θ)122(12(ej3θ?+e−j3θ)?+?32(ejθ?+e−jθ)).

As
cos(θ)?=?12(ejθ?+?e−jθ)??and??cos(3θ)?=?12(ej3θ?+?e−j3θ)
![]()
we get
cos3(θ)?=?14?cos(3θ)?+?34cos(θ).
![]()
The exponential form can be used to solve complex equations of the form zn = c, where c is a complex number. A particularly important example is the problem of finding all the solutions of zn = 1, called the n roots of unity.
The n roots of unity
To solve the equation zn = 1, we use the fact that 1 is a complex number with modulus 1 and argument 0, as can be seen in Figure 10.19(a). However, we can also use an argument of 2π, 4π, 6π, or any other multiple of 2π. As 2π is a complete revolution, adding 2π on to the argument of any complex number does not change the position of the vector representing it and therefore does not change the value of the number.

The equation zn= 1 can be expressed as
zn?=?ej2πN??where?N?∈?ℤ
![]()
We can solve this equation by taking the nth root of both sides, which is the same as taking both sides to the power 1 /n.
(zn)?1/n?=?ej2πN/n??where?N?∈?ℤ
![]()
We can substitute some values for N to find the various solutions also using the fact that there should be n roots to the equation zn= 1 so that we can stop after finding all n roots.
Example 10.21
Find all the solutions to z3 = 1.
Solution Write 1 as a complex number with argument 2π N giving the equation as
z3=?ej2πN??where?N?∈?ℤ.
![]()
Taking the cube root of both sides:
(z3)1/3=?ej(2πN/3)??where?N?∈?ℤ.
![]()
Substituting
N=0?:z=ej2π0=1N=1?:z=ej2π/3N=2?:z=ej4π/3.

There is no need to use any more values of N. We use the fact that there should be three roots of a cubic equation. If we continued to substitute values for N, then the values will begin to repeat. For example, substituting N = 3 gives z = ej2π3/3 = ej2π, which we know is the same as ej0 (subtracting 2π from the argument) which equals 1, which is a root that we have already found.
The solutions to z3= 1 are shown on an Argand diagram in Figure 10.20. The principal root of a complex equation is the one found nearest to the position of the positive x-axis. Notice that in the case of z3 = 1, the principal root is 1 and the other solutions can be obtained from another by rotation through 2π /3. Hence, another way of finding the n roots of zn= 1 is to start with the principal root of z = 1 = ej0 and add on multiples of 2π/n to the argument, in order to find the other roots.

Example 10.22
Find all the roots of z5 = 1
Solution One root, the principal root, is z = 1 = ej0. The other roots can be found by rotating this around the complex plane by multiples of 2π/5. Therefore, we have the solutions:
z=1,?ej2π/5,?ej4π/5,?ej6π/5,?ej8π/5.
![]()
These are shown in Figure 10.21.

