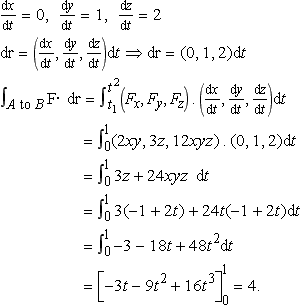Vector calculus
18.1 Introduction
In the previous chapter, we looked at functions of more than one variable. For a function of two variables (x, y) we define a function u = f (x, y) which can be represented by a surface. For each pair of values (x, y) we can find a single value for u, showing that u is a scalar quantity. For this reason, a function of spatial coordinates is called a scalar field. We also saw how to calculate a gradient of a function of two variables and that the gradient depends on the direction of the path that we choose across the surface. This means that the gradient must be described by both a magnitude and a direction. From Chapter 9, we know that vectors are used to represent quantities that have both magnitude and direction and we shall show in this chapter that we represent the gradient of a scalar field as a vector field.
A vector field is a vector function, which means that at each point in space the function has both magnitude and direction and can be expressed by a vector with x, y, and z components. In Chapter 6, we quoted many relationships between physical quantities that involve derivatives. There we considered only movement in a single spatial direction. Many of these equations should properly be described by vector field equations in space. In order to express these equations, we need to define the operations of divergence and curl of a vector field. Vector field equations are particularly important in electromagnetic field theory.
In this chapter we give an introduction to vector fields and operations on vector fields with applications to evaluating line and surface integrals.
18.2 The gradient of a scalar field
We define the gradient of a scalar field as follows
![]()
![]() is the gradient of φ or simply ‘grad
is the gradient of φ or simply ‘grad ![]() is called the ‘del’ operator. The meaning of this definition is that we take the partial derivative of the scalar field with respect to x, y, and z, and these are the components of our vector field.
is called the ‘del’ operator. The meaning of this definition is that we take the partial derivative of the scalar field with respect to x, y, and z, and these are the components of our vector field.
This definition is equivalent to
![]()
and also to
![]()
If ![]() is defined for two spatial dimensions (x, y) only then we would have
is defined for two spatial dimensions (x, y) only then we would have
![]()
Example 18.1
Given ![]() = x2 + xyz, find the vector field that describes its gradient.
= x2 + xyz, find the vector field that describes its gradient.
Solution We use
![]()
Differentiating ![]() partially with respect to x, y, and z, we find:
partially with respect to x, y, and z, we find:

Therefore, we find that
![]()
Direction of maximum slope
We would like to know why this vector function is called the gradient. We saw in the last chapter that a function of more than one variable has many derivatives associated with it, depending on the direction that we choose to measure it. We found that for a function of ![]() of two variables, along a path defined by (x(t), y(t)), the derivative of
of two variables, along a path defined by (x(t), y(t)), the derivative of ![]() is given by:
is given by:
![]()
Using the definition of the scalar product, we can write the above as
![]()
where (dx / dt, dy / dt) has components representing the rate of change of x and y and therefore gives the direction of the path in the (x, y) plane.
We also know from Chapter 9 that for two vectors a and b:
![]()
where a · b is the scalar product of vectors a and b, ![]() is the angle between them and a, b are their magnitudes. If the direction of b could be chosen in order to maximize this scalar product we would choose
is the angle between them and a, b are their magnitudes. If the direction of b could be chosen in order to maximize this scalar product we would choose ![]() because
because ![]() with the maximum value occurring at
with the maximum value occurring at ![]() where
where ![]() = 1. So to maximize the scalar product we choose the direction of b to be along a. So the direction of the path which maximizes the scalar product
= 1. So to maximize the scalar product we choose the direction of b to be along a. So the direction of the path which maximizes the scalar product
![]()
will be when the direction of (dx / dt, d y / dt) is the same as that of ![]() So
So ![]() gives the magnitude and direction of maximum gradient of
gives the magnitude and direction of maximum gradient of ![]() and the slope in any general direction can be found by taking the component of
and the slope in any general direction can be found by taking the component of ![]() in the direction of interest.
in the direction of interest.
Example 18.2
![]() describes its gradient, where x, y > 0 and find the maximum slope at the point (4,9,1).
describes its gradient, where x, y > 0 and find the maximum slope at the point (4,9,1).
Solution We use
![]()
Differentiating ![]() partially with respect to x, y, and z, we find:
partially with respect to x, y, and z, we find:
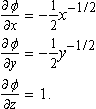
Therefore, we find that
![]()
Therefore, the maximum slope at the point (4, 9, 1) is given by substituting x = 4, y = 9, and z = 1 into the above expression for grad ![]() giving (−1/4, −1/6, 1). This has a magnitude of
giving (−1/4, −1/6, 1). This has a magnitude of
![]()
in a direction given by the unit vector
![]()
The  (del) operator
(del) operator
We defined
![]()
or equivalently
![]()
We can see that ∇ (del) can be considered as an operator defined by
![]()
or equivalently
![]()
This same operator can be used when differentiating vector fields.
18.3 Differentiating vector fields
We now consider vector fields, which represent a vector at each point in space. Therefore, we have the field F which has components in the x, y, and z directions, all of which are also functions of x, y, and z, that is
![]()
where Fx, Fy, Fzare all functions of x, y, and z.
There are two important fields that can be found by differentiating vector fields. The divergence of a vector field produces a scalar field and the curl of a vector field produces a vector field. These are defined as follows

The last expression can also be represented by using a determinant to define the cross-product of a vector. We have that
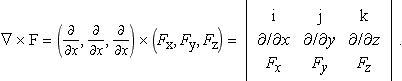
There is one more operator that is used in many equations of electromagnetic fields. This is the ‘del squared’ operator ![]() which operates on a scalar field. This is defined by
which operates on a scalar field. This is defined by
![]()
All of these operators are important in describing vector field relationships. For instance
![]()
represents the three-dimensional wave equation.
Example 18.3
![]()
Solution From the definition
![]()
we see that we find the scalar field by partially differentiating the first component by x, the second by y, and the third by z, and summing the result. Hence
![]()
To find ![]() we use the definition in terms of the determinant and expand about the first row, which in this case gives:
we use the definition in terms of the determinant and expand about the first row, which in this case gives:

Example 18.4
Show the vector identity
![]()
Solution Taking F = (Fx, Fy, Fz), we get from the definition of curl:
![]()
Now taking the divergence of the resulting vector field we take the dot product of
![]()
with the above giving

We use the fact that for functions with continuous partial derivatives
![]()
that is, the order of differentiation used to calculate higher-order partial derivatives is not important. Then all the terms in the above cancel out giving
![]()
18.4 The scalar line integral
The result of integrating a scalar field along a given curve is important for calculating many physical quantities. We know that in one dimension we relate the work done by a force in moving from one location to another as W = ∫ F dx, where F is the force, W is the work done or energy used and x is the distance moved in the direction of the force. In three dimensions, an object can move along a path and the position of the object will vary such that r = (x(t), y(t), z(t)) where t is some parameter used to describe the path taken. The work done in any given direction will be given by the component of the force in that direction multiplied by the distance moved. Hence we find:
![]()
where C is the path along which the object moves and r describes its position vector. To calculate this value we need to be able to integrate fields along a path, where the path is described in terms of a position vector, r = (x(t), y(t), z(t)).
We use
![]()
and the symbolic relationship
![]()
to give
![]()
and

where t1 and t2 are the values of the parameter at the start and end points of the curve C.
Example 18.5
Given F = 2xyzi – x2y j + z2x k, Find the integral of F along a path defined by 2t i – t j + k from t = 1 to t = 4.
Solution We have r = 2t i – 3t j + k, and therefore, x = 2t, y = −3t, and z = 1 giving
![]()
Therefore, we want to find
![]()
Substituting for x, y, z in terms of t, as above, we get

Example 18.6
Find
![]()
where F = (2xy, 3z, 12xyz), and C is a path clockwise around a triangle ABC with vertices A(1,0,–l), B (1,1,1), C (0,1,1).
Solution We need to integrate along each of the three sides of the triangle. We need, in each case to find the equation of the line along the side of the triangle. The vector equation of a line between two points a and b was found in Chapter 9 to be r = a(l – t)+ b t where t is some parameter and for points between A and B then 0≤t ≤ 1.
From A to B:r = (1,0, –1)(1 – t) + (1,1, l)t = (1, t, −1 + 2t). So x = 1, y = t, and z = − 1 + 2t, and

Therefore, the total integral around the path is given by the sum of the integral along the three sections – that is
![]()
Integrals round a closed curve
If we are calculating the line integral round a closed curve in a plane (where the field is a function of x and y only) we can use Green's theorem in a plane to convert the integral into a double integral over the enclosed surface. This theorem is as follows
![]()
The left-hand side of this expression represent the integral of F · dr, as before, however now we are limited to considering a plane so that r = (x, y) and also the path of integration must be closed. The fact that C is a closed path is indicated by the small circle on the integral sign.
Example 18.7
Using Green's theorem find the integral
![]()
where F = (3x2, −4xy), and C a path clockwise along the perimeter of the rectangle 0 ≤ x ≤ 4, 0 ≤ y ≤ 1.
Solution We want to find
![]()
which, by Green's theorem in the plane, is equal to
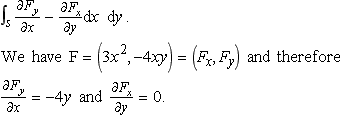
The surface is a rectangle so the limits for the integration are easy to establish as being for x from 0 to 4 and for y from 0 to 1. Hence, we get the surface integral.
![]()
To perform a multiple integral we simply do one integral and then integrate the result. The order of performing the integrations will not matter in this case because the limits of integration are independent of the other variable and the integrals exists and are continuous in the relevant region. We do the inner integration with respect to x. Here we are integrating −4 y, which does not contain a term in x, so we treat it as a constant for the purposes of the first integration giving the integral as −4 y x.
![]()
Now, we do the integration in y to give
![]()
18.5 Surface integrals
Many problems in field theory involve the calculation of flux of a vector field out of some enclosed surface. This requires us to integrate a vector field over the surface. Such problems are simplified by using the divergence theorem, which relates the integral of a vector field over a bounding surface to the integral of the divergence of the field over the enclosed volume.
![]()
S is a surface enclosing the volume V. This expresses the relationship between the amount of source material in a volume and the flux out of the enclosing surface. An example is the relationship between electric charge within a volume and the flux of the resulting electric field.
Example 18.8
Given F = (x – y + z, 2x2y, 1) find the integral of F over the closed surface consisting of the edges of the cube 0 ≤ x ≤ 3, 0 ≤ y ≤ 3 and 0 ≤ z ≤ 3.
Solution We want to use the divergence theorem
![]()
so we need to find the divergence of the vector field F = (x – y + z, 2x2 y, 1) giving Fx = x − y + z, Fy = 2x2y, and Fz = 1 and
![]()
The integral is
![]()
We can now perform each of the integrations one after the other. We begin with, the integration over x, which gives

Example 18.9
Use the divergence therem to evaluate the surface integral of F where R = e−(x+y+z) and S is the surface of a tetrahedron defined by the vertices (0,0,0), (1,0,0), (0,1,0), and (0,0,1).
Solution We use
![]()
but in order to express the limits of the integration we need to consider the geometry of the given tetrahedron. This is shown in Figure 18.1.

We can see from the figure that the sides of the tetrahedron lie along the x, y- and z-axes and the fourth side is the plane ABC, given by the equation x + y + z = 1. In this simple case, we can guess the equation of this plane and check that it is correct by substituting the values for the points A (1,0,0), B (0,1,0), and C (0,0,1). We need to choose the limits of integration so that we integrate correctly over this tetrahedron. x must start from 0 and go up to values lying on the plane ABC. This means that x is from 0 to 1 – y – z. If we integrate for x first then when considering the integration for y, we will have eliminated the x variable and will be left with the y, z plane. So y goes between y = 0 and the line BC, given by y = 1 – z. Finally, in considering z we have the values of z from 0 to 1. This gives:
![]()
We perform the integration with respect to x:

Now we integrate with respect to y:
![]()
Finally, integrating with respect to z we get:

18.6 Summary
1. A scalar field is a function of spatial coordinates giving a single, scalar value at every point (x, y, z).
2. The gradient of a scalar field φ grad φ is defined by:
![]()
3. The gradient of a scalar field gives the magnitude and direction of the maximum slope at any point r = (x, y, z) on φ.
4. ∇is the ‘del’ operator where
![]()

5. A vector field is a vector function of spatial coordinates, for example, F(x, y, z)= i Fx+ j Fy+ k Fz= (Fx, Fy, Fz)where Fx, Fy, Fzare all functions of x, y, and z.
6. The divergence and curl of a vector field are defined by

The expression for curl F can also be represented using a determinant, to define the cross product of two vectors. We have that:
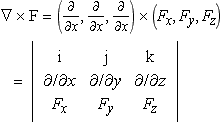
7. A line integral of a vector field, F, along some path C can be calculated by
![]()
where r = (x(t), y(t), z(t)) is the position vector of a position on the curve C represented using a parameter t and values t1 and t2 correspond to the end points of the path of C.
8. The line integral around a closed path in two dimensions can be converted to a surface integral by using Green's theorem in two dimensions:
![]()
This gives a double integral evaluated over the given surface in the plane.
9. A surface integral around a closed surface in three dimensions can be converted to a volume integral over the volume enclosed within the surface using the divergence theorem
![]()
This then gives a triple integral to be evaluated over the given volume.
18.7 Exercises
18.1. Given that φ = x2 – yz + 5z3, Ψ = x2y2Z, F = (xy, 3xyz, x –z), and G = (3z, 4x, 2), find
(b) ∇ ψ at (0.5, 0.1,0)
(c) ∇·F
(d) ∇xG
(e) curl (φ i + ψ j)
(f) div(ψ G)
(g) The magnitude of the maximum slope and the unit vector in the direction of the maximum slope of ψ at the point (1,2,0).
18.2. ϕ and ψ are scalar field functions of (x, y, z). Show the following vector identities:
![]()
18.3. Calculate
![]()
where
(a) F = (y2, x, zy) and C is along the line joining the points A (2,0,0) and B (1,1,0),
(b) F = x2yi + 2xy j + 3xyz k and C is along the path given by r = ti + (1 – t) j + t k for t from 1 to 3.
18.4. Find the work done by the force F = (3x, –2y, z) in the displacement along the curve y = x, z = 2x2 as x goes from 1 to 2.
18.5. Use Green's theorem in the plane to evaluate the following line integrals clockwise around the given closed curve
(a) F = xi + y 2j, where C is the perimeter of a rectangle ABCD where A = (0,0), B = (0,2), C = (1,2), and D = (1,0);
(b) F = (x– y)i + (–x –y)j where C is the perimeter of the square given by 1 ![]()
(c) F = (cos(y), sin(x)) where C is the region bounded by the lines x = 0, x = 1, y = −π /2, and y = π/2.
18.6. For the following vector fields, F, use the divergence theorem to evaluate the surface integrals over the surface, S, indicated:
(a) F = xyi + yzj + xzk, where S is the surface of the cube given by 0![]() and
and ![]()
(b) F = zi – y2 j and S is the surface of 0 ![]()
(c) F = (x+ y, x – z, x2 + z2) where S is the surface of a tetrahedron defined by the vertices (0,0,0), (1,0,0), (0,1,0), and (0,0,1).