18.2 THE POLYNOMIAL DIVISION ALGORITHM
Assume that the dividend polynomial A of degree n is given by
(18.1)
![]()
The divisor polynomial of degree m is given by
(18.2)
![]()
The polynomial division operation produces the quotient and remainder polynomials Q and R
(18.3)
![]()
(18.4)
![]()
where
(18.5)
![]()
The division operation is a series of multiply/subtract iterations such that after each iteration one coefficient of the quotient polynomial is obtained, in descending order. Also, a partial remainder polynomial having m terms is obtained after each iteration. At the end of the iterations, all the coefficients of Q are determined as well as the final remainder polynomial R.
The notation we use in this chapter for the partial remainder polynomials is as follows:
- R(i): input partial remainder polynomial at iteration i
- R(i + 1): resulting partial remainder polynomial at iteration i
- rj(i): jth coefficient of R(i), 0 ≤ j < m
According to the above definitions, can express R(i) explicitly as
(18.6)
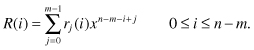
We can express the long-division algorithm for polynomials as an iteration using an LFSR as indicated in Algorithm 18.1.
Algorithm 18.1
Linear feedback shift register (LFSR) polynomial division algorithm
1: // Initialization of partial remainder R and q
2: qn−m = an
3: for j = 0 : m − 1 do
4: rj(0) = an−m+j
5: end for
6: // Start Iterations
7: for i = 0 : n − m do
8: for j = 1 : m − 1 do
9: rj(i + 1) = rj−1(i) + qn−m−ibj−1
10: end for
11: qn−m−i−1 = rm−1(i)
12: r0(i + 1) = an−m−i
13: end for
14: // Final remainder
15: for j = 0 : m − 1 do
16: rj = rj(n − m + 1)
17: end for
Note from the algorithm that the most significant coefficient of the divisor polynomial B is not used. Instead we use our knowledge of the rm−1(i) to directly estimate the quotient coefficient qm−n−i for ensuring that rm(i) = 0.
