Further Notes on Repeated-Measures Analyses
Advantages of the Repeated-Measures Design versus the Between-Subjects Design
An alternative to the repeated-measures design is a between-subjects design, as described in Chapter 9. For example, you could have followed a between-subjects design in which two groups would be measured at only one point in time: immediately following the weekend program (at Time 2, from Figure 12.3). In this between-subjects study, one group of couples would attend the weekend encounter, and the other group would not attend. If you conducted the study well, you could then attribute any differences in the group means to the weekend experience.
With both the repeated-measures design and the between-subjects design, the sums of squares and mean squares are computed in similar ways. However, an advantage of the repeated-measures design is that each participant serves as his or her own control. Since each participant serves in each treatment condition, variability in scores due to individual differences between participants will not be a factor in determining the size of the treatment effect. Between-subjects variability is removed from the error term in computing the F test (see Table 12.1). This computation usually allows for a more sensitive test of treatment effects because the between-subjects variance is typically much larger than the within-subjects variance. This is true because multiple observations from the same participant tend to be positively correlated, even when you obtain measures across time.
An additional advantage with repeated measures is increased efficiency since this design requires only half the number of participants that you would need in a between-subjects design. This might be an important consideration when the targeted study population is limited. These statistical and practical differences illustrate the importance of carefully planning your analyses when designing an experiment.
Weaknesses of the One-Way Repeated Measures Design
The primary limitation of the present design is the lack of a control group. Since all participants receive the treatment in this design, there is no comparison that you can make to evaluate if any observed changes are truly the result of the experimental manipulation. In the study just described, for example, increases in investment scores might occur because of time spent together and have nothing to do with the specific program activities during the weekend (i.e., the treatment). Chapter 13, “Factorial ANOVA with Repeated-Measures Factors and Between-Subjects Factors,” shows how you can remedy this weakness with the addition of an appropriate control group.
Another potential problem with this type of design is that participants might be affected by a treatment in a way that changes responses to subsequent measures. This problem is called a sequence effect.
Sequence Effects
An important consideration in a repeated measures design is the potential for certain experimental confounds. In particular, the experimenter must control for order effects and carry-over effects.
Order Effects
Order effects result when the ordinal position of the treatments biases participant responses. Consider this example. An experimenter studying perception requires participants to perform a reaction-time task in each of three conditions. Participants must depress a button on a response pad while waiting for a signal, and after receiving the signal they must depress a different button. The dependent variable is reaction time and the independent variable is the type of signal. The independent variable has three levels: in condition 1, the signal is a flash of light; in condition 2, it is an audio tone; in condition 3, it is both the light and tone simultaneously. Each test session consists of 50 trials. A mean reaction time is computed for each session. Assume that these conditions are presented in the same order for all participants (e.g., in the morning, before lunch, and after lunch).
The problem with this research design is that reaction-time scores might be adversely affected after lunch by fatigue. Responses to condition 3 might be more a measure of fatigue than a true treatment effect. For example, suppose the experiment yields mean scores for 10 participants as shown in Table 12.2. It appears that presentation of both signals (tone and light) causes a delayed reaction time compared to the other two treatments (tone alone or light alone).
| Type of Signal | ||
|---|---|---|
| Tone | Light | Tone and Light |
| 650 | 650 | 1125 |
An alternative explanation for the preceding results is that a fatigue effect in the early afternoon is causing the longer reaction times. According to this interpretation, you would expect each of the three treatments to have longer reaction times if presented during the early afternoon period. If you collected the data as described, there is no way to determine which explanation is correct.
To control for this problem, you must vary the treatment order. This technique, called counterbalancing, is used to present the conditions in different orders to different participants. A counterbalanced research design appears in Table 12.3:
| Treatment Order | |||
|---|---|---|---|
| AM | Late AM | Early PM | |
| Participant 1 | Tone | Light | Both |
| Participant 2 | Both | Tone | Light |
| Participant 3 | Light | Both | Tone |
| Participant 4 | Tone | Both | Light |
| Participant 5 | Light | Tone | Both |
| Participant 6 | Both | Light | Tone |
Note that in Table 12.3, each treatment occurs an equal number of times at each point of measurement. To achieve complete counterbalancing, you must use each combination of treatment sequences for an equal number of participants so that possible error due to order effects is dispersed evenly across treatment conditions.
Complete counterbalancing becomes impractical as the number of treatment conditions increases. For example, there are only 6 possible sequences of 3 treatments, but this increases to 24 sequences with 4 treatments, 120 sequences with 5 treatments, and so forth. Obviously, complete counterbalancing typically is feasible only if the independent variable can assume a relatively small number of values. |
Carryover Effects
Carryover effects occur when an effect from one treatment changes (carries over to) participants’ responses in the following treatment condition. For example, suppose you are investigating the hypnotic effect of three different drugs. Drug 1 is given on night 1, and sleep onset latency is measured by electroencephalogram. The same measure is collected on nights 2 and 3, when drugs 2 and 3 are administered. If drug 1 has a long half-life (e.g., flurazepam), then it may still exert an effect on sleep latency at night 2. This carryover effect would make it impossible to accurately assess the effect of drug 2.
To avoid potential carryover effects, the experimenter might decide to separate the experimental conditions by one week. Counterbalancing also provides some control over carryover effects. If all treatment combinations can be given, then each treatment will be followed (and preceded) by each other treatment with equal frequency.
However, carryover effects are not as likely to even out with counterbalancing as are order effects. The advantage of counterbalancing might lie more in enabling the experimenter to measure the extent of carryover effects and to make appropriate adjustments to the analysis.
Ideally, careful consideration of experimental design will allow the experimenter to avoid significant carryover effects in a study. This is another consideration when choosing between a repeated-measures and a between-subjects design. In the study of drug effects described above, the investigator can avoid any possible carryover effects by using a between-subjects design. In that design, each participant would receive only one of the drug treatments.
Validity Conditions for the Univariate One-Way ANOVA, Repeated-Measures Design
The analysis described previously was conducted as a conventional univariate repeated-measures ANOVA. This analysis is valid only if certain assumptions about the data hold true. Two assumptions for this test are normality and homogeneity of covariance. Statisticians have pointed out that, in many instances, data collected under real-world conditions do not meet the second assumption.
The violation of homogeneity of covariance is particularly problematic for repeated measures designs as compared to between-subjects designs. In the case of between-subjects designs, the analysis still produces a robust F test even when this assumption is not met (provided sample sizes are equal). On the other hand, a violation of this assumption with a repeated measures design leads to an increased probability of a Type I error (i.e., rejection of a true null hypothesis). Therefore, you must take greater care when analyzing repeated measures designs to either prove that the assumptions of the test have been met or alter the analysis to account for the effects of the violation.
A discussion of the validity conditions for the univariate ANOVA and alternative approaches to the analysis of repeated measures data appears next. This section merely introduces some of the relevant issues and is not intended as an exhaustive description of the statistical problems inherent with use of repeated measures analyses. For a more detailed treatment, see Barcikowski and Robey (1984) or LaTour and Miniard (1983).
The assumptions underlying a valid application of the conventional F test are that criterion scores from the experimental treatments have a multivariate normal distribution in the population (i.e., normality) and that the common covariance matrix has a spherical pattern (i.e., homogeneity of covariance). Normality is impossible to prove but becomes more likely as sample size increases.
Homogeneity of covariance refers to the covariance between participants for any two treatments. One way to conceptualize this is that participants should have the same rankings in scores for all pairs of levels of the independent variable. For example, if there are three treatment (Tx) conditions, the covariance between Tx1 and Tx2 should be comparable to the covariance between Tx2 and Tx3, and to the covariance between Tx1 and Tx3.
If there are only two levels of the independent variable, then this assumption is automatically satisfied because there is only one covariance value. |
Homogeneity of covariance is sufficient for test validity, but a less-specific type of covariance pattern (i.e., sphericity) is a necessary validity condition (Huynh & Mandeville, 1979; Rouanet & Lepine, 1970). SAS performs a test for sphericity if you request the PRINTE option in the REPEATED statement. The general form for this option is as follows:
REPEATED trial-variable-name #levels CONTRAST (level#) / SUMMARY
PRINTE;The REPEATED statement from the actual program is as follows:
3 REPEATED TIME 3 CONTRAST (1) / SUMMARY PRINTE;
Revising the program presented earlier so that it includes the PRINTE option results in seven pages of output. The results requested by the PRINTE option would appear on pages 3 and 4. Those pages appear here as Output 12.3:
Output 12.3. Results of Test for Sphericity Requested by PRINTE Option
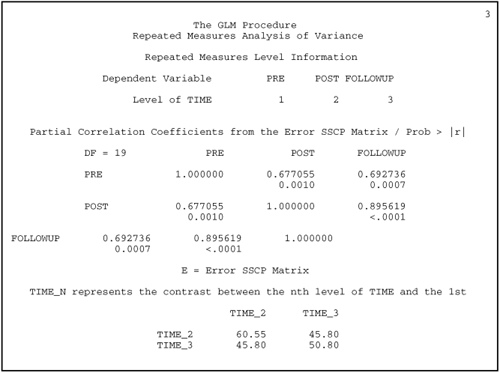

The test performed with orthogonal components is the test of interest. In Output 12.3, this test appears toward the middle of output page 4 under “Sphericity Tests,” to the right of “Orthogonal Components,” under the heading “Mauchly’s Criterion.”
In Output 12.3, this test is significant at approximately p = .03. Technically, a significant p value indicates that the data display significant non-sphericity and thus departure from the homogeneity of covariance assumption. Be warned, however, that this test is extremely sensitive and any deviation from sphericity results in a significant F test. However, you can compensate for small to moderate deviations from sphericity through use of an adjusted F test (discussion follows). If there is a severe departure from sphericity (e.g., p < .01), then another approach to the problem is to use multivariate tests.
Alternate Analyses
If the assumptions of the test are not met, then various alternatives to the conventional univariate ANOVA have been proposed. These alternatives consist of modifications of the univariate ANOVA or use of the multivariate ANOVA.
Modified Univariate Tests
As stated above, the primary concern when the sphericity pattern is not present is that the F test will be too liberal and lead to inappropriate rejection of the null hypothesis (i.e., Type I error). Therefore, modifications that are recommended to compensate for non-sphericity are generally aimed at making the test more conservative.
The currently accepted method to modify the F test to account for deviations from sphericity is to adjust the degrees of freedom associated with the F value. Several correction factors have been developed to accomplish this. The correction factor is named epsilon (Greenhouse & Geisser, 1959). Epsilon varies between a lower limit of [1/(k–1)] and 1, depending on the degree to which the data deviate from a spherical pattern. The degrees of freedom are multiplied by the correction factor to yield a number that is either lower or unchanged. Therefore, a given test typically has fewer degrees of freedom and requires a greater F value to achieve a given p level. With epsilon at a value of 1 (meaning the assumption has been met), the degrees of freedom are unchanged. To the extent that sphericity is not present, epsilon is reduced and this further decreases the degrees of freedom to produce a more conservative test.
The computations for epsilon are performed routinely by SAS as part of the univariate analysis for repeated measures. (See page 4 of Output 12.2.) Although the exact procedure to follow is somewhat controversial and can depend on characteristics specific to a given dataset, there is some consensus for use of the following general guidelines:
You should use the adjusted univariate test when the Greenhouse-Geisser (G-G) epsilon is greater than or equal to .75.
If the G-G epsilon is less than .75, a multivariate analysis (MANOVA) provides a more powerful test.
A Greenhouse-Geisser (G-G) epsilon value of approximately .76 (p < .05) was previously reported in Output 12.2. According to the above guidelines, this value suggests use of the adjusted F test.
Multivariate ANOVA
As a repeated-measures design consists of within-subjects observations across treatment conditions, the individual treatment measures can be viewed as separate, correlated dependent variables. Thereby the dataset is easily conceptualized as multivariate even though the design is univariate, and it can be analyzed with multivariate statistics. In this type of analysis, each level of the repeated factor is treated as a separate variable. The SAS program described earlier in this chapter computes a multivariate ANOVA automatically, and includes the results in the output. The statistics for the multivariate test appear on page 3 of Output 12.2. SAS computes four test statistics, and the appropriate test to use depends on the characteristics of your dataset. For a review of the statistical literature on this topic, see Olson (1976).
The multivariate ANOVA has an advantage over the univariate test in that it requires no assumption of sphericity. Some statisticians recommend that the multivariate ANOVA be used frequently, if not routinely, with repeated measures designs (Davidson, 1972). This argument is made for several reasons.
In selecting a test statistic, it is always desirable to choose the most powerful test. A test is said to have power when it is able to correctly reject the null hypothesis. In many situations, the univariate ANOVA is more powerful than the MANOVA and is therefore the better choice. However, the test to determine if the assumption of sphericity has been met is not very powerful with small samples. Therefore, only when the n is large (i.e., 20 greater than the number of treatment levels or n > k + 20) does the test for sphericity have sufficient power. Remember that the multivariate test becomes just as powerful as the univariate test as the n grows larger. This, however, creates a sort of catch-22: with a small n, there is no certainty that the assumptions underlying the univariate ANOVA have been met; with a large n, the MANOVA is equal to, if not more powerful than, the univariate test.
Others argue that the univariate approach offers a more powerful test for many types of data and should not be so readily abandoned (Tabachnick & Fidell, 2001). In their view, the multivariate ANOVA should be reserved for those situations that cannot be analyzed with the univariate ANOVA.
With the current example, the sample is composed of 20 participants and thus falls below the sensitivity threshold for sphericity tests described above (i.e., n < k + 20). In other words, the decision to reject the null hypothesis of significant departure from the homogeneity of covariance assumption (i.e., Mauchly’s Criterion of .68, p < .05) might not be correct. Fortunately, both the standard and adjusted F values (as well as the multivariate statistics) suggest rejection of the study’s null hypothesis of no difference in investment scores across the three points in time.
