35. Cache Oblivious Data Structures

The memory system of most modern computers consists of a hierarchy of memory levels, with each level acting as a cache for the next; for a typical desktop computer the hierarchy consists of registers, level 1 cache, level 2 cache, level 3 cache, main memory, and disk. One of the essential characteristics of the hierarchy is that the memory levels get larger and slower the further they get from the processor, with the access time increasing most dramatically between main memory and disk. Another characteristic is that data is moved between levels in large blocks. As a consequence of this, the memory access pattern of an algorithm has a major influence on its practical running time. Unfortunately, the RAM model (Figure 35.1) traditionally used to design and analyze algorithms is not capable of capturing this, since it assumes that all memory accesses take equal time.

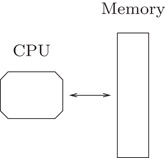
Figure 35.1The RAM model.

Because of the shortcomings of the RAM model, a number of more realistic models have been proposed in recent years. The most successful of these models is the simple two-level I/O-model introduced by Aggarwal and Vitter [1] (Figure 35.2). In this model the memory hierarchy is assumed to consist of a fast memory of size M and a slower infinite memory, and data is transfered between the levels in blocks of B consecutive elements. Computation can only be performed on data in the fast memory, and it is assumed that algorithms have complete control over transfers of blocks between the two levels. We denote such a transfer a memory transfer. The complexity measure is the number of memory transfers needed to solve a problem. The strength of the I/O model is that it captures part of the memory hierarchy, while being sufficiently simple to make design and analysis of algorithms feasible. In particular, it adequately models the situation where the memory transfers between two levels of the memory hierarchy dominate the running time, which is often the case when the size of the data exceeds the size of main memory. Agarwal and Vitter showed that comparison based sorting and searching require Θ(SortM,B(N))=Θ(NBlogM/BNB) $Θ ({Sort}_{M, B} (N)) = Θ (\frac{N}{B} \log_{M / B} \frac{N}{B})$ and Θ(log_B N) memory transfers in the I/O-model, respectively [1]. Subsequently a large number of other results have been obtained in the model; see the surveys by Arge [2] and Vitter [3] for references. Also see Chapter 28.

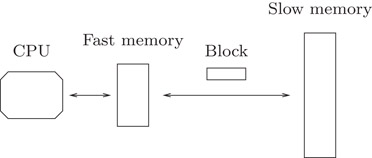
Figure 35.2The I/O model.

More elaborate models of multi-level memory than the I/O-model have been proposed (see, e.g., [3] for an overview) but these models have been less successful, mainly because of their complexity. A major shortcoming of the proposed models, including the I/O-model, have also been that they assume that the characteristics of the memory hierarchy (the level and block sizes) are known. Very recently however, the cache-oblivious model, which assumes no knowledge about the hierarchy, was introduced by Frigo et al. [4]. In essence, a cache-oblivious algorithm is an algorithm formulated in the RAM model but analyzed in the I/O model, with the analysis required to hold for any B and M. Memory transfers are assumed to be performed by an off-line optimal replacement strategy. The beauty of the cache-oblivious model is that since the I/O-model analysis holds for any block and memory size, it holds for all levels of a multi-level memory hierarchy (see [4] for details). In other words, by optimizing an algorithm to one unknown level of the memory hierarchy, it is optimized on all levels simultaneously. Thus the cache-oblivious model is effectively a way of modeling a complicated multi-level memory hierarchy using the simple two-level I/O-model.

Frigo et al. [4] described optimal Θ(Sort_{M, B}(N)) memory transfer cache-oblivious algorithms for matrix transposition, fast Fourier transform, and sorting; Prokop also described a static search tree obtaining the optimal O(log_B N) transfer search bound [5]. Subsequently, Bender et al. [6] described a cache-oblivious dynamic search trees with the same search cost, and simpler and improved cache-oblivious dynamic search trees were then developed by several authors [7–10]. Cache-oblivious algorithms have also been developed for, for example, problems in computational geometry [7,11,12], for scanning dynamic sets [7], for layout of static trees [13], for partial persistence [7], and for a number of fundamental graph problems [14] using cache-oblivious priority queues [14,15]. Most of these results make the so-called tall cache assumption, that is, they assume that M > Ω(B2); we make the same assumption throughout this chapter.

Empirical investigations of the practical efficiency of cache-oblivious algorithms for sorting [16], searching [9,10,17] and matrix problems [4] have also been performed. The overall conclusion of these investigations is that cache-oblivious methods often outperform RAM algorithms, but not always as much as algorithms tuned to the specific memory hierarchy and problem size. On the other hand, cache-oblivious algorithms perform well on all levels of the memory hierarchy, and seem to be more robust to changing problem sizes than cache-aware algorithms.

In the rest of this chapter we describe some of the most fundamental and representative cache-oblivious data structure results. In Section 35.2 we discuss two fundamental primitives used to design cache-oblivious data structures. In Section 35.3 we describe two cache-oblivious dynamic search trees, and in Section 35.4 two priority queues. Finally, in Section 35.5 we discuss structures for 2-dimensional orthogonal range searching.

35.2Fundamental Primitives

The most fundamental cache-oblivious primitive is scanning—scanning an array with N elements incurs Θ(NB) $Θ (\frac{N}{B})$ memory transfers for any value of B. Thus algorithms such as median finding and data structures such as stacks and queues that only rely on scanning are automatically cache-oblivious. In fact, the examples above are optimal in the cache-oblivious model. Other examples of algorithms that only rely on scanning include Quicksort and Mergesort. However, they are not asymptotically optimal in the cache-oblivious model since they use O(NBlogNM) $O (\frac{N}{B} \log \frac{N}{M})$ memory transfers rather than Θ(Sort_{M, B} (N)).

Apart from algorithms and data structures that only utilize scanning, most cache-oblivious results use recursion to obtain efficiency; in almost all cases, the sizes of the recursive problems decrease double-exponentially. In this section we describe two of the most fundamental such recursive schemes, namely the van Emde Boas layout and the k-merger.

35.2.1Van Emde Boas Layout

One of the most fundamental data structures in the I/O-model is the B-tree [18]. A B-tree is basically a fanout Θ(B) tree with all leaves on the same level. Since it has height O(log_B N) and each node can be accessed in O(1) memory transfers, it supports searches in O(log_B N) memory transfers. It also supports range queries, that is, the reporting of all K elements in a given query range, in O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ memory transfers. Since B is an integral part of the definition of the structure, it seems challenging to develop a cache-oblivious B-tree structure. However, Prokop [5] showed how a binary tree can be laid out in memory in order to obtain a (static) cache-oblivious version of a B-tree. The main idea is to use a recursively defined layout called the van Emde Boas layout closely related to the definition of a van Emde Boas tree [19]. The layout has been used as a basic building block of most cache-oblivious search structures (e.g., in [6–11,13]).

35.2.1.1Layout

For simplicity, we only consider complete binary trees. A binary tree is complete if it has N = 2h − 1 nodes and height h for some integer h. The basic idea in the van Emde Boas layout of a complete binary tree T $T$ with N leaves is to divide T $T$ at the middle level and lay out the pieces recursively (Figure 35.3). More precisely, if T $T$ only has one node it is simply laid out as a single node in memory. Otherwise, we define the top tree T0 $T_{0}$ to be the subtree consisting of the nodes in the topmost ⌊h/2⌋ levels of T $T$ , and the bottom trees T1,…,Tk $T_{1}, \dots, T_{k}$ to be the Θ(N−−√) $Θ (\sqrt{N})$ subtrees rooted in the nodes on level ⌈h/2⌉ of T $T$ ; note that all the subtrees have size Θ(N−−√) $Θ (\sqrt{N})$ . The van Emde Boas layout of T $T$ consists of the van Emde Boas layout of T0 $T_{0}$ followed by the van Emde Boas layouts of T1,…,Tk $T_{1}, \dots, T_{k}$ .

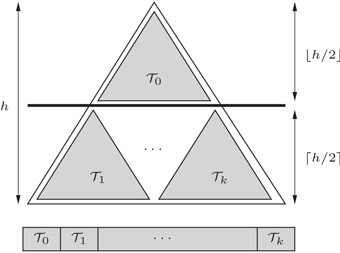
Figure 35.3The van Emde Boas layout.

35.2.1.2Search

To analyze the number of memory transfers needed to perform a search in T $T$ , that is, traverse a root-leaf path, we consider the first recursive level of the van Emde Boas layout where the subtrees are smaller than B. As this level T $T$ is divided into a set of base trees of size between Θ(B−−√) $Θ (\sqrt{B})$ and Θ(B), that is, of height Ω(log B) (Figure 35.4). By the definition of the layout, each base tree is stored in O(B) contiguous memory locations and can thus be accessed in O(1) memory transfers. That the search is performed in O(log_B N) memory transfers then follows since the search path traverses O((log N)/ log B) = O(log_B N) different base trees.

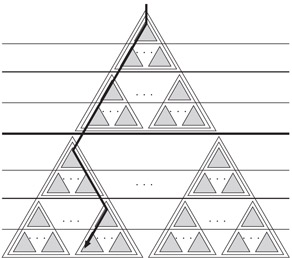
Figure 35.4A search path.

35.2.1.3Range query

To analyze the number of memory transfers needed to answer a range query [x1, x2] on T $T$ using the standard recursive algorithm that traverses the relevant parts of T $T$ (starting at the root), we first note that the two paths to x1 and x2 are traversed in O(log_B N) memory transfers. Next we consider traversed nodes v that are not on the two paths to x1 and x2. Since all elements in the subtree Tv $T_{v}$ rooted at such a node v are reported, and since a subtree of height log B stores Θ(B) elements, O(KB) $O (\frac{K}{B})$ subtrees Tv $T_{v}$ of height log B are visited. This in turn means that the number of visited nodes above the last log B levels of T $T$ is also O(KB) $O (\frac{K}{B})$ ; thus they can all be accessed in O(KB) $O (\frac{K}{B})$ memory transfers. Consider the smallest recursive level of the van Emde Boas layout that completely contain Tv $T_{v}$ . This level is of size between Ω(B) and O(B2) (Figure 35.5a). On the next level of recursion Tv $T_{v}$ is broken into a top part and O(B−−√) $O (\sqrt{B})$ bottom parts of size between Ω(B−−√) $Ω (\sqrt{B})$ and O(B) each (Figure 35.5b). The top part is contained in a recursive level of size O(B) and is thus stored within O(B) consecutive memory locations; therefore it can be accessed in O(1) memory accesses. Similarly, the O(B) nodes in the O(B−−√) $O (\sqrt{B})$ bottom parts are stored consecutively in memory; therefore they can all be accessed in a total of O(1) memory transfers. Therefore, the optimal paging strategy can ensure that any traversal of Tv $T_{v}$ is performed in O(1) memory transfers, simply by accessing the relevant O(1) blocks. Thus overall a range query is performed in O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ memory transfers.

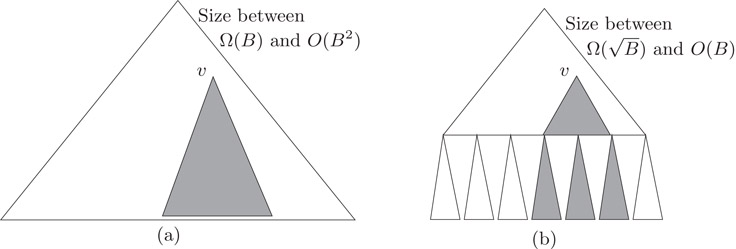
Figure 35.5Traversing tree Tv $T_{v}$ with O(B) leaves; (a) smallest recursive van Emde Boas level containing Tv $T_{v}$ has size between Ω(B) and O(B2); (b) next level in recursive subdivision.

Theorem 35.1

Let T $T$ be a complete binary tree with N leaves laid out using the van Emde Boas layout. The number of memory transfers needed to perform a search (traverse a root-to-leaf path) and a range query in T $T$ is O(log_B N) and O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ , respectively.

Note that the navigation from node to node in the van Emde Boas layout is straight-forward if the tree is implemented using pointers. However, navigation using arithmetic on array indexes is also possible [9]. This avoids the use of pointers and hence saves space.

The constant in the O(log_B N) bound for searching in Theorem 35.1 can be seen to be four. Further investigations of which constants are possible for cache-oblivious comparison based searching appear in [20].

35.2.2k-Merger

In the I/O-model the two basic optimal sorting algorithms are multi-way versions of Mergesort and distribution sorting (Quicksort) [1]. Similarly, Frigo et al. [4] showed how both merge based and distribution based optimal cache-oblivious sorting algorithms can be developed. The merging based algorithm, Funnelsort, is based on a so-called k-merger. This structure has been used as a basic building block in several cache-oblivious algorithms. Here we describe a simplified version of the k-merger due to Brodal and Fagerberg [12].

35.2.2.1Binary mergers and merge trees

A binary merger merges two sorted input streams into a sorted output stream: In one merge step an element is moved from the head of one of the input streams to the tail of the output stream; the heads of the input streams, as well as the tail of the output stream, reside in buffers of a limited capacity.

Binary mergers can be combined to form binary merge trees by letting the output buffer of one merger be the input buffer of another—in other words, a binary merge tree is a binary tree with mergers at the nodes and buffers at the edges, and it is used to merge a set of sorted input streams (at the leaves) into one sorted output stream (at the root). Refer to Figure 35.6 for an example.

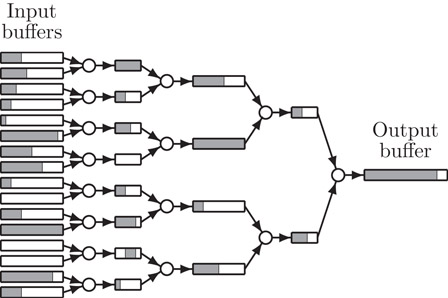
Figure 35.6A 16-merger consisting of 15 binary mergers. Shaded parts represent elements in buffers.

An invocation of a binary merger in a binary merge tree is a recursive procedure that performs merge steps until the output buffer is full (or both input streams are exhausted); if an input buffer becomes empty during the invocation (and the corresponding stream is not exhausted), the input buffer is recursively filled by an invocation of the merger having this buffer as output buffer. If both input streams of a merger get exhausted, the corresponding output stream is marked as exhausted. A procedure FILL(v) performing an invocation of a binary merger v is shown in Figure 35.7 (ignoring exhaustion issues). A single invocation FILL(r) on the root r of a merge tree will merge the streams at the leaves of the tree.

Figure 35.7Invocation of binary merger v.

35.2.2.2k-merger

A k-merger is a binary merge tree with specific buffer sizes. For simplicity, we assume that k is a power of two, in which case a k-merger is a complete binary tree of k − 1 binary mergers. The output buffer at the root has size k3, and the sizes of the rest of the buffers are defined recursively in a manner resembling the definition of the van Emde Boas layout: Let i = log k be the height of the k-merger. We define the top tree to be the subtree consisting of all mergers of depth at most ⌈i/2⌉, and the bottom trees to be the subtrees rooted in nodes at depth ⌈i/2⌉ + 1. We let the edges between the top and bottom trees have buffers of size k^3/2, and define the sizes of the remaining buffers by recursion on the top and bottom trees. The input buffers at the leaves hold the input streams and are not part of the k-merger definition. The space required by a k-merger, excluding the output buffer at the root, is given by S(k) = k^1/2 · k^3/2 + (k^1/2 + 1) · S(k^1/2), which has the solution S(k) = Θ(k2).

We now analyze the number of memory transfers needed to fill the output buffer of size k3 at the root of a k-merger. In the recursive definition of the buffer sizes in the k-merger, consider the first level where the subtrees (excluding output buffers) have size less than M/3; if k¯ $\bar{k}$ is the number of leaves of one such subtree, we by the space usage of k-mergers have k¯2≤M/3 ${\bar{k}}^{2} \leq M / 3$ and (k¯2)2=k¯4=Ω(M) $({\bar{k}}^{2})^{2} = {\bar{k}}^{4} = Ω (M)$ . We call these subtrees of the k-merger base trees and the buffers between the base trees large buffers. Assuming B2 ≤ M/3, a base tree Tv $T_{v}$ rooted in v together with one block from each of the large buffers surrounding it (i.e., its single output buffer and k¯ $\bar{k}$ input buffers) can be contained in fast memory, since M/3+B+k¯⋅B≤M/3+B+(M/3)1/2⋅(M/3)1/2≤M $M / 3 + B + \bar{k} \cdot B \leq M / 3 + B + (M / 3)^{1 / 2} \cdot (M / 3)^{1 / 2} \leq M$ . If the k-merger consists of a single base tree, the number of memory transfers used to fill its output buffer with k3 elements during an invocation is trivially O(k3/B + k). Otherwise, consider an invocation of the root v of a base tree Tv $T_{v}$ , which will fill up the size Ω(k¯3) $Ω ({\bar{k}}^{3})$ output buffer of v. Loading Tv $T_{v}$ and one block for each of the k¯ $\bar{k}$ buffers just below it into fast memory will incur O(k¯2/B+k¯) $O ({\bar{k}}^{2} / B + \bar{k})$ memory transfers. This is O(1/B) memory transfer for each of the Ω(k¯3) $Ω ({\bar{k}}^{3})$ elements output, since k¯4=Ω(M) ${\bar{k}}^{4} = Ω (M)$ implies k¯2=Ω(M1/2)=Ω(B) ${\bar{k}}^{2} = Ω (M^{1 / 2}) = Ω (B)$ , from which k¯=O(k¯3/B) $\bar{k} = O ({\bar{k}}^{3} / B)$ follows. Provided that none of the input buffers just below Tv $T_{v}$ become empty, the output buffer can then be filled in O(k¯3/B) $O ({\bar{k}}^{3} / B)$ memory transfers since elements can be read from the input buffers in O(1/B) transfers amortized. If a buffer below Tv $T_{v}$ becomes empty, a recursive invocation is needed. This invocation may evict Tv $T_{v}$ from memory, leading to its reloading when the invocation finishes. We charge this cost to the Ω(k¯3) $Ω ({\bar{k}}^{3})$ elements in the filled buffer, or O(1/B) memory transfers per element. Finally, the last time an invocation is used to fill a particular buffer, the buffer may not be completely filled (due to exhaustion). However, this happens only once for each buffer, so we can pay the cost by charging O(1/B) memory transfers to each position in each buffer in the k-merger. As the entire k-merger uses O(k2) space and merges k3 elements, these charges add up to O(1/B) memory transfers per element.

We charge an element O(1/B) memory transfers each time it is inserted into a large buffer. Since k¯=Ω(M1/4) $\bar{k} = Ω (M^{1 / 4})$ , each element is inserted in O(logk¯k)=O(logMk3) $O (\log_{\bar{k}} k) = O (\log_{M} k^{3})$ large buffers. Thus we have the following.

Theorem 35.2

Excluding the output buffers, the size of a k-merger is O(k2) and it performs O(k3BlogMk3+k) $O (\frac{k^{3}}{B} \log_{M} k^{3} + k)$ memory transfers during an invocation to fill up its output buffer of size k3.

35.2.2.3Funnelsort

The cache-oblivious sorting algorithm Funnelsort is easily obtained once the k-merger structure is defined: Funnelsort breaks the N input elements into N^1/3 groups of size N^2/3, sorts them recursively, and then merges the sorted groups using an N^1/3-merger.

Funnelsort can be analyzed as follows: Since the space usage of a k-merger is sub-linear in its output, the elements in a recursive sort of size M/3 only need to be loaded into memory once during the entire following recursive sort. For k-mergers at the remaining higher levels in the recursion tree, we have k3 ≥ M/3 ≥ B2, which implies k2 ≥ B^4/3 > B and hence k3/B > k. By Theorem 35.2, the number of memory transfers during a merge involving N′ elements is then O(log_M(N′)/B) per element. Hence, the total number of memory transfers per element is

O (1 B (1 + \sum i = 0 \infty log M N (2 / 3) i)) = O ((log M N) / B) .

$O (\frac{1}{B} (1 + \sum_{i = 0}^{\infty} \log_{M} N^{(2 / 3)^{i}})) = O ((\log_{M} N) / B) .$

Since log_M x = Θ(log_M/B x) when B2 ≤ M/3, we have the following theorem.

Theorem 35.3

Funnelsort sorts N element using O(Sort_{M, B}(N)) memory transfers.

In the above analysis, the exact (tall cache) assumption on the size of the fast memory is B2 ≤ M/3. In [12] it is shown how to generalize Funnelsort such that it works under the weaker assumption B^{1 + ɛ} ≤ M, for fixed ɛ > 0. The resulting algorithm incurs the optimal O(Sort_{M, B}(N)) memory transfers when B^{1 + ɛ} = M, at the price of incurring O(1/ɛ · Sort_{M, B}(N)) memory transfers when B2 ≤ M. It is shown in [21] that this trade-off is the best possible for comparison based cache-oblivious sorting.

35.3Dynamic B-Trees

The van Emde Boas layout of a binary tree provides a static cache-oblivious version of B-trees. The first dynamic solution was given Bender et al. [6], and later several simplified structures were developed [7–10]. In this section, we describe two of these structures [7,9].

35.3.1Density Based

In this section we describe the dynamic cache-oblivious search tree structure of Brodal et al. [9]. A similar proposal was given independently by Bender et al. [8].

The basic idea in the structure is to embed a dynamic binary tree of height log N + O(1) into a static complete binary tree, that is, in a tree with 2h − 1 nodes and height h, which in turn is embedded into an array using the van Emde Boas layout. Refer to Figure 35.8.

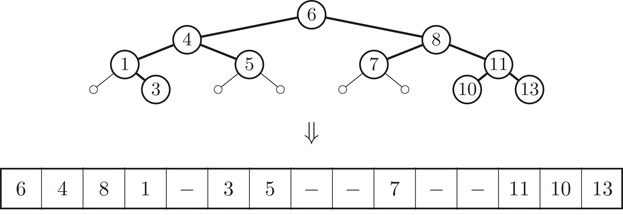
Figure 35.8Illustration of embedding a height H tree into a complete static tree of height H, and the van Emde Boas layout of this tree.

To maintain the dynamic tree we use techniques for maintaining small height in a binary tree developed by Andersson and Lai [22]; in a different setting, similar techniques has also been given by Itai et al. [23]. These techniques give an algorithm for maintaining height log N + O(1) using amortized O(log2N) time per update. If the height bound is violated after performing an update in a leaf l, this algorithm performs rebalancing by rebuilding the subtree rooted at a specific node v on the search path from the root to l. The subtree is rebuilt to perfect balance in time linear in the size of the subtree. In a binary tree of perfect balance the element in any node v is the median of all the elements stored in the subtree Tv $T_{v}$ rooted in v. This implies that only the lowest level in Tv $T_{v}$ is not completely filled and the empty positions appearing at this level are evenly distributed across the level. Hence, the net effect of the rebuilding is to redistribute the empty positions in Tv $T_{v}$ . Note that this can lower the cost of future insertions in Tv $T_{v}$ , and consequently it may in the long run be better to rebuild a subtree larger than strictly necessary for reestablishment of the height bound. The criterion for choosing how large a subtree to rebuild, that is, for choosing the node v, is the crucial part of the algorithms by Andersson and Lai [22] and Itai et al. [23]. Below we give the details of how they can be used in the cache-oblivious setting.

35.3.1.1Structure

As mentioned, the data structure consists of a dynamic binary tree T $T$ embedded into a static complete binary tree T′ $T^{'}$ of height H, which in turn is embedded into an array using the van Emde Boas layout.

In order to present the update and query algorithms, we define the density ρ(u) of a node u as |T_u|/|T′_u|, where |T_u| and |T′_u| are the number of nodes in the trees rooted in u in T $T$ and T′ $T^{'}$ , respectively. In Figure 35.8, the node containing the element 4 has balance 4/7. We also define two density thresholds τ_i and γ_i for the nodes on each level i = 1, 2, …, H (where the root is at level 1). The upper density thresholds τ_i are evenly space values between 3/4 and 1, and the lower density thresholds γ_i are evenly spaced values between 1/4 and 1/8. More precisely, τ_i = 3/4 + (i − 1)/(4(H − 1)) and γ_i = 1/4 − (i − 1)/(8(H − 1)).

35.3.1.2Updates

To insert a new element into the structure we first locate the position in T $T$ of the new node w. If the insertion of w violates the height bound H, we rebalance T $T$ as follows: First we find the lowest ancestor v of w satisfying γ_i ≤ ρ(v) ≤ τ_i, where i is the level of v. If no ancestor v satisfies the requirement, we rebuild the entire structure, that is, T $T$ , T′ $T^{'}$ and the layout of T′ $T^{'}$ : For k the integer such that 2k ≤ N < 2^{k + 1} we choose the new height H of the tree T′ $T^{'}$ as k + 1 if N ≤ 5/4 · 2k; otherwise we choose H = k + 2. On the other hand, if the ancestor v exists we rebuild Tv $T_{v}$ : We first create a sorted list of all elements in Tv $T_{v}$ by an in-order traversal of Tv $T_{v}$ . The ⌈|T_v|/2⌉th element becomes the element stored at v, the smallest ⌊(|T_v| − 1)/2⌋ elements are recursively distributed in the left subtree of v, and the largest ⌈(|T_v| − 1)/2⌉ elements are recursively distributed in the right subtree of v.

We can delete an element from the structure in a similar way: We first locate the node w in T $T$ containing the element e to be deleted. If w is not a leaf and has a right subtree, we then locate the node w′ containing the immediate successor of e (the node reached by following left children in the right subtree of w), swap the elements in w and w′, and let w = w′. We repeat this until w is a leaf. If on the other hand w is not a leaf but only has a left subtree, we instead repeatedly swap w with the node containing the predecessor of e. Finally, we delete the leaf w from T $T$ , and rebalance the tree by rebuilding the subtree rooted at the lowest ancestor v of w satisfying satisfying γ_i ≤ ρ(v) ≤ τ_i, where i is the level of v; if no such node exists we rebuild the entire structure completely.

Similar to the proof of Andersson and Lai [22] and Itai et al. [23] that updates are performed in O(log2N) time, Brodal et al. [9] showed that using the above algorithms, updates can be performed in amortized O(log_B N + (log2N)/B) memory transfers.

35.3.1.3Range queries

In Section 35.2, we discussed how a range query can be answered in O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ memory transfers on a complete tree T′ $T^{'}$ laid out using the van Emde Boas layout. Since it can be shown that the above update algorithm maintains a lower density threshold of 1/8 for all nodes, we can also perform range queries in T $T$ efficiently: To answer a range query [x1, x2] we traverse the two paths to x1 and x2 in T $T$ , as well as O(log N) subtrees rooted in children of nodes on these paths. Traversing one subtree Tv $T_{v}$ in T $T$ incurs at most the number of memory transfers needed to traverse the corresponding (full) subtree T′v $T_{v}^{'}$ in T′ $T^{'}$ . By the lower density threshold of 1/8 we know that the size of T′v $T_{v}^{'}$ is at most a factor of eight larger than the size of Tv $T_{v}$ . Thus a range query is answered in O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ memory transfers.

Theorem 35.4

There exists a linear size cache-oblivious data structure for storing N elements, such that updates can be performed in amortized O(log_B N + (log2N)/B) memory transfers and range queries in O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ memory transfers.

Using the method for moving between nodes in a van Emde Boas layout using arithmetic on the node indices rather than pointers, the above data structure can be implemented as a single size O(N) array of data elements. The amortized complexity of updates can also be lowered to O(log_B N) by changing leaves into pointers to buckets containing Θ(log N) elements each. With this modification a search can still be performed in O(log_B N) memory transfers. However, then range queries cannot be answered efficiently, since the O(KlogN) $O (\frac{K}{\log N})$ buckets can reside in arbitrary positions in memory.

35.3.2Exponential Tree Based

The second dynamic cache-oblivious search tree we consider is based on the so-called exponential layout of Bender et al. [7]. For simplicity, we here describe the structure slightly differently than in [7].

35.3.2.1Structure

Consider a complete balanced binary tree T $T$ with N leaves. Intuitively, the idea in an exponential layout of T $T$ is to recursively decompose T $T$ into a set of components, which are each laid out using the van Emde Boas layout. More precisely, we define component C0 $C_{0}$ to consist of the first 12logN $\frac{1}{2} \log N$ levels of T $T$ . The component C0 $C_{0}$ contains N−−√ $\sqrt{N}$ nodes and is called an N-component because its root is the root of a tree with N leaves (that is, T $T$ ). To obtain the exponential layout of T $T$ , we first store C0 $C_{0}$ using the van Emde Boas layout, followed immediately by the recursive layout of the N−−√ $\sqrt{N}$ subtrees, T1,T2,…,TN√ $T_{1}, T_{2}, \dots, T_{\sqrt{N}}$ , of size N−−√ $\sqrt{N}$ , beneath C0 $C_{0}$ in T $T$ , ordered from left to right. Note how the definition of the exponential layout naturally defines a decomposition of T $T$ into log log N + O(1) layers, with layer i consisting of a number of N1/2i−1 $N^{1 / 2^{i - 1}}$ -components. An X-component is of size Θ(X−−√) $Θ (\sqrt{X})$ and its Θ(X−−√) $Θ (\sqrt{X})$ leaves are connected to X−−√ $\sqrt{X}$ -components. Thus the root of an X-component is the root of a tree containing X elements. Refer to Figure 35.9. Since the described layout of T $T$ is really identical to the van Emde Boas layout, it follows immediately that it uses linear space and that a root-to-leaf path can be traversed in O(log_B N) memory transfers.

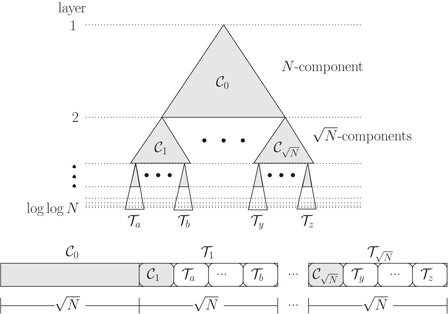
Figure 35.9Components and exponential layout.

By slightly relaxing the requirements on the layout described above, we are able to maintain it dynamically: We define an exponential layout of a balanced binary tree T $T$ with N leaves to consist of a composition of T $T$ into log log N + O(1) layers, with layer i consisting of a number of N^{1/2^{i − 1}}-components, each laid out using the van Emde Boas layout (Figure 35.9). An X-component has size Θ(X−−√) $Θ (\sqrt{X})$ but unlike above we allow its root to be root in a tree containing between X and 2X elements. Note how this means that an X-component has between X/2X−−√=12X−−√ $X / 2 \sqrt{X} = \frac{1}{2} \sqrt{X}$ and 2X/X−−√=2X−−√ $2 X / \sqrt{X} = 2 \sqrt{X}$ leaves. We store the layout of T $T$ in memory almost as previously: If the root of T $T$ is root in an X-component C0 $C_{0}$ , we store C0 $C_{0}$ first in 2⋅2X−−√−1 $2 \cdot 2 \sqrt{X} - 1$ memory locations (the maximal size of an X-component), followed immediately by the layouts of the subtrees (X−−√ $\sqrt{X}$ -components) rooted in the leaves of C0 $C_{0}$ (in no particular order). We make room in the layout for the at most 2X−−√ $2 \sqrt{X}$ such subtrees. This exponential layout for T $T$ uses S(N)=Θ(N−−√)+2N−−√⋅S(N−−√) $S (N) = Θ (\sqrt{N}) + 2 \sqrt{N} \cdot S (\sqrt{N})$ space, which is Θ(N log N).

35.3.2.2Search

Even with the modified definition of the exponential layout, we can traverse any root-to-leaf path in T $T$ in O(log_B N) memory transfers: The path passes through exactly one N^{1/2^{i − 1}}-component for 1 ≤ i ≤ log log N + O(1). Each X-component is stored in a van Emde Boas layout of size Θ(X−−√) $Θ (\sqrt{X})$ and can therefore be traversed in Θ(logBX−−√) $Θ (\log_{B} \sqrt{X})$ memory transfers (Theorem 35.1). Thus, if we use at least one memory transfer in each component, we perform a search in O(log_B N) + log log N memory accesses. However, we do not actually use a memory transfer for each of the log log N + O(1) components: Consider the traversed X-component with B−−√≤X≤B $\sqrt{B} \leq X \leq B$ . This component is of size O(B−−√) $O (\sqrt{B})$ and can therefore be loaded in O(1) memory transfers. All smaller traversed components are of total size O(B−−√logB−−√)=O(B) $O (\sqrt{B} \log \sqrt{B}) = O (B)$ , and since they are stored in consecutively memory locations they can also be traversed in O(1) memory transfers. Therefore only O(1) memory transfers are used to traverse the last log log B − O(1) components. Thus, the total cost of traversing a root-to-leaf path is O(log_B N + log log N − log log B) = O(log_B N).

35.3.2.3Updates

To perform an insertion in T $T$ we first search for the leaf l where we want to perform the insertion; inserting the new element below l will increase the number of elements stored below each of the log log N + O(1) components on the path to the root, and may thus result in several components needing rebalancing (an X-component with 2X elements stored below it). We perform the insertion and rebalance the tree in a simple way as follows: We find the topmost X-component Cj $C_{j}$ on the path to the root with 2X elements below it. Then we divide these elements into two groups of X elements and store them separately in the exponential layout (effectively we split Cj $C_{j}$ with 2X elements below it into two X-components with X elements each). This can easily be done in O(X) memory transfers. Finally, we update a leaf and insert a new leaf in the X2-component above Cj $C_{j}$ (corresponding to the two new X-components); we can easily do so in O(X) memory transfers by rebuilding it. Thus overall we have performed the insertion and rebalancing in O(X) memory transfers. The rebuilding guarantees that after rebuilding an X-component, X inserts have to be performed below it before it needs rebalancing again. Therefore we can charge the O(X) cost to the X insertions that occurred below Cj $C_{j}$ since it was last rebuilt, and argue that each insertion is charged O(1) memory accesses on each of the log log N + O(1) levels. In fact, using the same argument as above for the searching cost, we can argue that we only need to charge an insertion O(1) transfers on the last log log B − O(1) levels of T $T$ , since rebalancing on any of these levels can always be performed in O(1) memory transfers. Thus overall we perform an insertion in O(log_B N) memory transfers amortized.

Deletions can easily be handled in O(log_B N) memory transfers using global rebuilding: To delete the element in a leaf l of T $T$ we simply mark l as deleted. If l’s sibling is also marked as deleted, we mark their parent deleted too; we continue this process along one path to the root of T $T$ . This way we can still perform searches in O(log_B N) memory transfers, as long as we have only deleted a fraction of the elements in the tree. After N2 $\frac{N}{2}$ deletes we therefore rebuild the entire structure in O(N log_B N) memory accesses, or O(log_B N) accesses per delete operation.

Bender et al. [7] showed how to modify the update algorithms to perform updates “lazily” and obtain worst case O(log_B N) bounds.

35.3.2.4Reducing space usage

To reduce the space of the layout of a tree T $T$ to linear we simply make room for 2 log N elements in each leaf, and maintain that a leaf contains between log N and 2 log N elements. This does not increase the O(log_B N) search and update costs since the O(log N) elements in a leaf can be scanned in O((log N)/B) = O(log_B N) memory accesses. However, it reduces the number of elements stored in the exponential layout to O(N/ log N).

Theorem 35.5

The exponential layout of a search tree T $T$ on N elements uses linear space and supports updates in O(log_B N) memory accesses and searches in O(log_B N) memory accesses.

Note that the analogue of Theorem 35.1 does not hold for the exponential layout, that is, it does not support efficient range queries. The reason is partly that the X−−√ $\sqrt{X}$ -components below an X-component are not located in (sorted) order in memory because components are rebalanced by splitting, and partly because of the leaves containing Θ(log N) elements. However, Bender et al. [7] showed how the exponential layout can be used to obtain a number of other important results: The structure as described above can easily be extended such that if two subsequent searched are separated by d elements, then the second search can be performed in O(log^*d + log_B d) memory transfers. It can also be extended such that R queries (batched searching) can be answered simultaneously in O(RlogBNR+SortM,B(R)) $O (R \log_{B} \frac{N}{R} + {Sort}_{M, B} (R))$ memory transfers. The exponential layout can also be used to develop a persistent B-tree, where updates can be performed in the current version of the structure and queries can be performed in the current as well as all previous versions, with both operations incurring O(log_B N) memory transfers. It can also be used as a basic building block in a linear space planar point location structure that answers queries in O(log_B N) memory transfers.

35.4Priority Queues

A priority queue maintains a set of elements with a priority (or key) each under the operations INSERT and DELETEMIN, where an INSERT operation inserts a new element in the queue, and a DELETEMIN operation finds and deletes the element with the minimum key in the queue. Frequently we also consider a DELETE operation, which deletes an element with a given key from the priority queue. This operation can easily be supported using INSERT and DELETEMIN: To perform a DELETE we insert a special delete-element in the queue with the relevant key, such that we can detect if an element returned by a DELETEMIN has really been deleted by performing another DELETEMIN.

A balanced search tree can be used to implement a priority queue. Thus the existence of a dynamic cache-oblivious B-tree immediately implies the existence of a cache-oblivious priority queue where all operations can be performed in O(log_B N) memory transfers, where N is the total number of elements inserted. However, it turns out that one can design a priority queue where all operations can be performed in Θ(SortM,B(N)/N)=O(1BlogM/BNB) $Θ ({Sort}_{M, B} (N) / N) = O (\frac{1}{B} \log_{M / B} \frac{N}{B})$ memory transfers; for most realistic values of N, M, and B, this bound is less than 1 and we can, therefore, only obtain it in an amortized sense. In this section we describe two different structures that obtain these bounds [14,15].

35.4.1Merge Based Priority Queue: Funnel Heap

The cache-oblivious priority queue Funnel Heap due to Brodal and Fagerberg [15] is inspired by the sorting algorithm Funnelsort [4,12]. The structure only uses binary merging; essentially it is a heap-ordered binary tree with mergers in the nodes and buffers on the edges.

35.4.1.1Structure

The main part of the Funnel Heap structure is a sequence of k-mergers (Section 35.2.2) with double-exponentially increasing k, linked together in a list using binary mergers; refer to Figure 35.10. This part of the structure constitutes a single binary merge tree. Additionally, there is a single insertion buffer I.

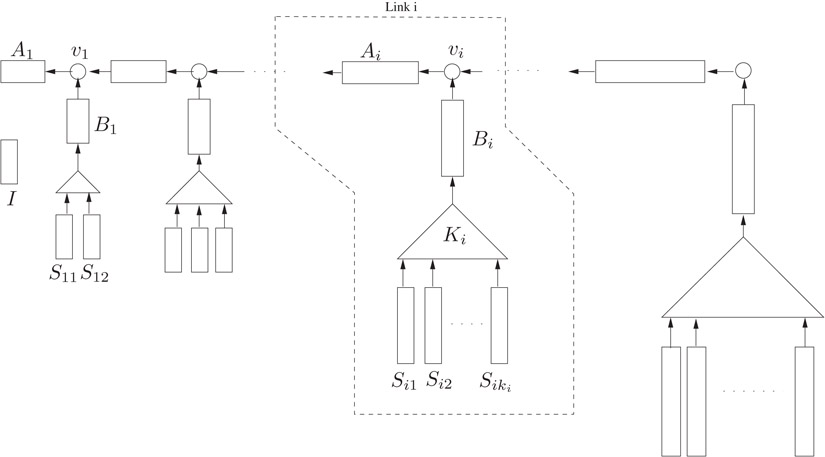
Figure 35.10Funnel Heap: Sequence of k-mergers (triangles) linked together using buffers (rectangles) and binary mergers (circles).

More precisely, let k_i and s_i be values defined inductively by

$(k 1, s 1) = (2, 8), s i + 1 = s i (k i + 1), k i + 1 = ⌈ ⌈ s i + 1 1 / 3 ⌉ ⌉,$ $\begin{matrix} (k_{1}, s_{1}) = (2, 8), \\ s_{i + 1} = s_{i} (k_{i} + 1), \\ k_{i + 1} = ⌈ ⌈ {s_{i + 1}}^{1 / 3} ⌉ ⌉, \end{matrix}$	(35.1)

where ⌈⌈x⌉⌉ denotes the smallest power of two above x, that is, ⌈⌈x⌉⌉ = 2^{⌈ log x⌉}. We note that s_i^1/3 ≤ k_i < 2s_i^1/3, from which s_i^4/3 < s_{i + 1} < 3s_i^4/3 follows, so both s_i and k_i grow double-exponentially: si+1=Θ(s4/3i) $s_{i + 1} = Θ (s_{i}^{4 / 3})$ and ki+1=Θ(k4/3i) $k_{i + 1} = Θ (k_{i}^{4 / 3})$ . We also note that by induction on i we have si=s1+∑i−1j=1kjsj $s_{i} = s_{1} + \sum_{j = 1}^{i - 1} k_{j} s_{j}$ for all i.

A Funnel Heap consists of a linked list with link i containing a binary merger v_i, two buffers A_i and B_i, and a k_i-merger K_i having k_i input buffers S_i1,…, S_{ik_i}. We refer to B_i, K_i, and S_i1,…, S_{ik_i} as the lower part of the link. The size of both A_i and B_i is k3i $k_{i}^{3}$ , and the size of each S_ij is s_i. Link i has an associated counter c_i for which 1 ≤ c_i ≤ k_i + 1. The initial value of c_i is one for all i. The structure also has one insertion buffer I of size s1. We maintain the following invariants:

Invariant 35.1

For link i, S_{ic_i},…, S_{ik_i} are empty.

Invariant 35.2

On any path in the merge tree from some buffer to the root buffer A1, elements appear in decreasing order.

Invariant 35.3

Elements in buffer I appear in sorted order.

Invariant 35.2 can be rephrased as the entire merge tree being in heap order. It implies that in all buffers in the merge tree, the elements appear in sorted order, and that the minimum element in the queue will be in A1 or I, if buffer A1 is non-empty. Note that an invocation (Figure 35.7) of any binary merger in the tree maintains the invariants.

35.4.1.2Layout

The Funnel Heap is laid out in consecutive memory locations in the order I, link 1, link 2,…, with link i being laid out in the order c_i, A_i, v_i, B_i, K_i, S_i1, S_i2,…, S_{ik_i}.

35.4.1.3Operations

To perform a DELETEMIN operation we compare the smallest element in I with the smallest element in A1 and remove the smallest of these; if A1 is empty we first perform an invocation of v1. The correctness of this procedure follows immediately from Invariant 35.2.

To perform an INSERT operation we insert the new element among the (constant number of) elements in I, maintaining Invariant 35.3. If the number of elements in I is now s1, we examine the links in order to find the lowest index i for which c_i ≤ k_i. Then we perform the following SWEEP(i) operation.

In SWEEP(i), we first traverse the path p from A1 to S_{ic_i} and record how many elements are contained in each encountered buffer. Then we traverse the part of p going from A_i to S_{ic_i}, remove the elements in the encountered buffers, and form a sorted stream σ1 of the removed elements. Next we form another sorted stream σ2 of all elements in links 1,…, i − 1 and in buffer I; we do so by marking A_i temporarily as exhausted and calling DELETEMIN repeatedly. We then merge σ1 and σ2 into a single stream σ, and traverse p again while inserting the front (smallest) elements of σ in the buffers on p such that they contain the same numbers of elements as before we emptied them. Finally, we insert the remaining elements from σ into S_{ic_i}, reset c_l to one for l = 1,2,…, i − 1, and increment c_i.

To see that SWEEP(i) does not insert more than the allowed s_i elements into S_{ic_i}, first note that the lower part of link i is emptied each time c_i is reset to one. This implies that the lower part of link i never contains more than the number of elements inserted into S_i1, S_i2,…, S_{ik_i} by the at most k_i SWEEP(i) operations occurring since last time c_i was reset. Since si=s1+∑i−1j=1kjsj $s_{i} = s_{1} + \sum_{j = 1}^{i - 1} k_{j} s_{j}$ for all i, it follows by induction on time that no instance of SWEEP(i) inserts more than s_i elements into S_{ic_i}.

Clearly, SWEEP(i) maintains Invariants 35.1 and 35.3, since I and the lower parts of links 1,…, i − 1 are empty afterwards. Invariant 35.2 is also maintained, since the new elements in the buffers on p are the smallest elements in σ, distributed such that each buffer contains exactly the same number of elements as before the SWEEP(i) operation. After the operation, an element on this path can only be smaller than the element occupying the same location before the operation, and therefore the merge tree is in heap order.

35.4.1.4Analysis

To analyze the amortized cost of an INSERT or DELETEMIN operation, we first consider the number of memory transfers used to move elements upwards (towards A1) by invocations of binary mergers in the merge tree. For now we assume that all invocations result in full buffers, that is, that no exhaustions occur. We imagine charging the cost of filling a particular buffer evenly to the elements being brought into the buffer, and will show that this way an element from an input buffer of K_i is charged O(1BlogM/Bsi) $O (\frac{1}{B} \log_{M / B} s_{i})$ memory transfers during its ascent to A1.

Our proof rely on the optimal replacement strategy keeping as many as possible of the first links of the Funnel Heap in fast memory at all times. To analyze the number of links that fit in fast memory, we define Δ_i to be the sum of the space used by links 1 to i and define i_M to be the largest i for which Δ_i ≤ M. By the space bound for k-mergers in Theorem 35.2 we see that the space used by link i is dominated by the Θ(s_i k_i) = Θ(k_i⁴) space use of S_i1,…, S_{ik_i}. Since ki+1=Θ(k4/3i) $k_{i + 1} = Θ (k_{i}^{4 / 3})$ , the space used by link i grows double-exponentially with i. Hence, Δ_i is a sum of double-exponentially increasing terms and is therefore dominated by its last term. In other words, Δ_i = Θ(k_i⁴) = Θ(s_i^4/3). By the definition of i_M we have Δ_{i_M} ≤ M < Δ_{i_M + 1}. Using si+1=Θ(s4/3i) $s_{i + 1} = Θ (s_{i}^{4 / 3})$ we see that log_M(s_{i_M}) = Θ(1).

Now consider an element in an input buffer of K_i. If i ≤ i_M the element will not get charged at all in our charging scheme, since no memory transfers are used to fill buffers in the links that fit in fast memory. So assume i > i_M. In that case the element will get charged for the ascent through K_i to B_i and then through v_j to A_j for j = i, i − 1,…, i_M. First consider the cost of ascending through K_i: By Theorem 35.2, an invocation of the root of K_i to fill B_i with k3i $k_{i}^{3}$ elements incurs O(ki+ki3BlogM/Bki3) $O (k_{i} + \frac{{k_{i}}^{3}}{B} \log_{M / B} {k_{i}}^{3})$ memory transfers altogether. Since M<ΔiM+1=Θ(k4iM+1) $M < Δ_{i_{M} + 1} = Θ (k_{i_{M} + 1}^{4})$ we have M = O(k_i⁴). By the tall cache assumption M = Ω(B2) we get B = O(k_i²), which implies k_i = O(k_i³/B). Under the assumption that no exhaustions occur, that is, that buffers are filled completely, it follows that an element is charged O(1BlogM/Bki3)=O(1BlogM/Bsi) $O (\frac{1}{B} \log_{M / B} {k_{i}}^{3}) = O (\frac{1}{B} \log_{M / B} s_{i})$ memory transfers to ascend through K_i and into B_i. Next consider the cost of ascending through v_j, that is, insertion into A_j, for j = i, i − 1,…, i_M: Filling of A_j incurs O(1 + |A_j|/B) memory transfers. Since B=O(k2iM+1)=O(k8/3iM) $B = O (k_{i_{M} + 1}^{2}) = O (k_{i_{M}}^{8 / 3})$ and |A_j| = k_j³, this is O(|A_j|/B) memory transfers, so an element is charged O(1/B) memory transfers for each A_j (under the assumption of no exhaustions). It only remains to bound the number of such buffers A_j, that is, to bound i − i_M. From s4/3i<si+1 $s_{i}^{4 / 3} < s_{i + 1}$ we have s(4/3)i−iMiM<si $s_{i_{M}}^{(4 / 3)^{i - i_{M}}} < s_{i}$ . Using log_M(s_{i_M}) = Θ(1) we get i − i_M = O(log log_M s_i). From log log_M s_i = O(log_M s_i) and the tall cache assumption M = Ω(B2) we get i − i_M = O(log_M s_i) = O(log_M/B s_i). In total we have proved our claim that, assuming no exhaustions occur, an element in an input buffer of K_i is charged O(1BlogM/Bsi) $O (\frac{1}{B} \log_{M / B} s_{i})$ memory transfers during its ascent to A1.

We imagine maintaining the credit invariant that each element in a buffer holds enough credits to be able to pay for the ascent from its current position to A1, at the cost analyzed above. In particular, an element needs O(1BlogM/Bsi) $O (\frac{1}{B} \log_{M / B} s_{i})$ credits when it is inserted in an input buffer of K_i. The cost of these credits we will attribute to the SWEEP(i) operation inserting it, effectively making all invocations of mergers be prepaid by SWEEP(i) operations.

A SWEEP(i) operation also incurs memory transfers by itself; we now bound these. In the SWEEP(i) operation we first form σ1 by traversing the path p from A1 to S_{ic_i}. Since the links are laid out sequentially in memory, this traversal at most constitutes a linear scan of the consecutive memory locations containing A1 through K_i. Such a scan takes O((Δ_{i − 1} + |A_i| + |B_i| + |K_i|)/B) = O(k_i³/B) = O(s_i/B) memory transfers. Next we form σ2 using DELETEMIN operations; the cost of which is paid for by the credits placed on the elements. Finally, we merge of σ1 and σ2 into σ, and place some of the elements in buffers on p and some of the elements in S_{ic_i}. The number of memory transfers needed for this is bounded by the O(s_i/B) memory transfers needed to traverse p and S_{ic_i}. Hence, the memory transfers incurred by the SWEEP(i) operation itself is O(s_i/B).

After the SWEEP(i) operation, the credit invariant must be reestablished. Each of the O(s_i) elements inserted into S_{ic_i} must receive O(1BlogM/Bsi) $O (\frac{1}{B} \log_{M / B} s_{i})$ credits. Additionally, the elements inserted into the part of the path p from A1 through A_{i − 1} must receive enough credits to cover their ascent to A1, since the credits that resided with elements in the same positions before the operations were used when forming σ2 by DELETEMIN operations. This constitutes O(Δ_{i − 1}) = o(s_i) elements, which by the analysis above, must receive O(1BlogM/Bsi) $O (\frac{1}{B} \log_{M / B} s_{i})$ credits each. Altogether O(si/B)+O(siBlogM/Bsi)=O(siBlogM/Bsi) $O (s_{i} / B) + O (\frac{s_{i}}{B} \log_{M / B} s_{i}) = O (\frac{s_{i}}{B} \log_{M / B} s_{i})$ memory transfers are attributed to a SWEEP(i) operation, again under the assumption that no exhaustions occur during invocations.

To actually account for exhaustions, that is, the memory transfers incurred when filling buffers that become exhausted, we note that filling a buffer partly incurs at most the same number of memory transfers as filling it entirely. This number was analyzed above to be O(|A_i|/B) for A_i and O(|Bi|BlogM/Bsi) $O (\frac{| B_{i} |}{B} \log_{M / B} s_{i})$ for B_i, when i > i_M. If B_i become exhausted, only a SWEEP(i) can remove that status. If A_i become exhausted, only a SWEEP(j) for j ≥ i can remove that status. As at most a single SWEEP(j) with j > i can take place between one SWEEP(i) and the next, B_i can only become exhausted once for each SWEEP(i), and A_i can only become exhausted twice for each SWEEP(i). From |A_i| = |B_i| = k_i³ = Θ(s_i) it follows that charging SWEEP(i) an additional cost of O(siBlogM/Bsi) $O (\frac{s_{i}}{B} \log_{M / B} s_{i})$ memory transfers will cover all costs of filling buffers when exhaustion occurs.

Overall we have shown that we can account for all memory transfers if we attribute O(siBlogM/Bsi) $O (\frac{s_{i}}{B} \log_{M / B} s_{i})$ memory transfers to each SWEEP(i). By induction on i, we can show that at least s_i insertions have to take place between each SWEEP(i). Thus, if we charge the SWEEP(i) cost to the last s_i insertions preceding the SWEEP(i), each insertion is charged O(1BlogM/Bsi) $O (\frac{1}{B} \log_{M / B} s_{i})$ memory transfers. Given a sequence of operation on an initial empty priority queue, let i_max be the largest i for which SWEEP(i) takes place. We have s_{i_max} ≤ N, where N is the number of insertions in the sequence. An insertion can be charged by at most one SWEEP(i) for i = 1,…, i_max, so by the double-exponential growth of s_i, the number of memory transfers charged to an insertion is

O (\sum k = 0 \infty 1 B log M / B N (3 / 4) k) = O (1 B log M / B N) = O (1 B log M / B N B),

$O (\sum_{k = 0}^{\infty} \frac{1}{B} \log_{M / B} N^{(3 / 4)^{k}}) = O (\frac{1}{B} \log_{M / B} N) = O (\frac{1}{B} \log_{M / B} \frac{N}{B}),$

where the last equality follows from the tall cache assumption M = Ω(B2).

Finally, we bound the space use of the entire structure. To ensure a space usage linear in N, we create a link i when it is first used, that is, when the first SWEEP(i) occurs. At that point in time, c_i, A_i, v_i, B_i, K_i, and S_i1 are created. These take up Θ(s_i) space combined. At each subsequent SWEEP(i) operation, we create the next input buffer S_{ic_i} of size s_i. As noted above, each SWEEP(i) is preceded by at least s_i insertions, from which an O(N) space bound follows. To ensure that the entire structure is laid out in consecutive memory locations, the structure is moved to a larger memory area when it has grown by a constant factor. When allocated, the size of the new memory area is chosen such that it will hold the input buffers S_ij that will be created before the next move. The amortized cost of this is O(1/B) per insertion.

Theorem 35.6

Using Θ(M) fast memory, a sequence of N INSERT, DELETEMIN, and DELETE operations can be performed on an initially empty Funnel Heap using O(N) space in O(1BlogM/BNB) $O (\frac{1}{B} \log_{M / B} \frac{N}{B})$ amortized memory transfers each.

Brodal and Fagerberg [15] gave a refined analysis for a variant of the Funnel Heap that shows that the structure adapts to different usage profiles. More precisely, they showed that the ith insertion uses amortized O(1BlogM/BNiB) $O (\frac{1}{B} \log_{M / B} \frac{N_{i}}{B})$ memory transfers, where N_i can be defined in any of the following three ways: (a) N_i is the number of elements present in the priority queue when the ith insertion is performed, (b) if the ith inserted element is removed by a DELETEMIN operation prior to the jth insertion then N_i = j − i, or (c) N_i is the maximum rank of the ith inserted element during its lifetime in the priority queue, where rank denotes the number of smaller elements in the queue.

35.4.2Exponential Level Based Priority Queue

While the Funnel Heap is inspired by Mergesort and uses k-mergers as the basic building block, the exponential level priority queue of Arge et al. [14] is somewhat inspired by distribution sorting and uses sorting as a basic building block.

35.4.2.1Structure

The structure consists of Θ(log log N) levels whose sizes vary from N to some small size c below a constant threshold c_t; the size of a level corresponds (asymptotically) to the number of elements that can be stored within it. The i’th level from above has size N^{(2/3)^{i − 1}} and for convenience we refer to the levels by their size. Thus the levels from largest to smallest are level N, level N^2/3, level N^4/9,…, level X^9/4, level X^3/2, level X, level X^2/3, level X^4/9,…, level c^9/4, level c^3/2, and level c. In general, a level can contain any number of elements less than or equal to its size, except level N, which always contains Θ(N) elements. Intuitively, smaller levels store elements with smaller keys or elements that were more recently inserted. In particular, the minimum key element and the most recently inserted element are always in the smallest (lowest) level c. Both insertions and deletions are initially performed on the smallest level and may propagate up through the levels.

Elements are stored in a level in a number of buffers, which are also used to transfer elements between levels. Level X consists of one up buffer uX that can store up to X elements, and at most X^1/3 down buffers dX1,…,dXX1/3 $d_{1}^{X}, \dots, d_{X^{1 / 3}}^{X}$ each containing between (1/2)X^2/3 and 2X^2/3 elements. Thus level X can store up to 3X elements. We refer to the maximum possible number of elements that can be stored in a buffer as the size of the buffer. Refer to Figure 35.11. Note that the size of a down buffer at one level matches the size (up to a constant factor) of the up buffer one level down.

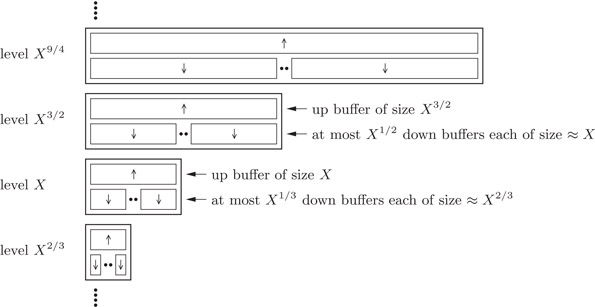
Figure 35.11Levels X^2/3, X, X^3/2, and X^9/4 of the priority queue data structure.

We maintain three invariants about the relationships between the elements in buffers of various levels:

Invariant 35.4

At level X, elements are sorted among the down buffers, that is, elements in dXi $d_{i}^{X}$ have smaller keys than elements in dXi+1 $d_{i + 1}^{X}$ , but elements within dXi $d_{i}^{X}$ are unordered.

The element with largest key in each down buffer dXi $d_{i}^{X}$ is called a pivot element. Pivot elements mark the boundaries between the ranges of the keys of elements in down buffers.

Invariant 35.5

At level X, the elements in the down buffers have smaller keys than the elements in the up buffer.

Invariant 35.6

The elements in the down buffers at level X have smaller keys than the elements in the down buffers at the next higher level X^3/2.

The three invariants ensure that the keys of the elements in the down buffers get larger as we go from smaller to larger levels of the structure. Furthermore, an order exists between the buffers on one level: keys of elements in the up buffer are larger than keys of elements in down buffers. Therefore, down buffers are drawn below up buffers on Figure 35.11. However, the keys of the elements in an up buffer are unordered relative to the keys of the elements in down buffers one level up. Intuitively, up buffers store elements that are “on their way up,” that is, they have yet to be resolved as belonging to a particular down buffer in the next (or higher) level. Analogously, down buffers store elements that are “on their way down”—these elements are by the down buffers partitioned into several clusters so that we can quickly find the cluster of smallest key elements of size roughly equal to the next level down. In particular, the element with overall smallest key is in the first down buffer at level c.

35.4.2.2Layout

The priority queue is laid out in memory such that the levels are stored consecutively from smallest to largest with each level occupying a single region of memory. For level X we reserve space for exactly 3X elements: X for the up buffer and 2X^2/3 for each possible down buffer. The up buffer is stored first, followed by the down buffers stored in an arbitrary order but linked together to form an ordered linked list. Thus O(∑log3/2logcNi=0N(2/3)i)=O(N) $O (\sum_{i = 0}^{\log_{3 / 2} \log_{c} N} N^{(2 / 3)^{i}}) = O (N)$ is an upper bound on the total memory used by the priority queue.

35.4.2.3Operations

To implement the priority queue operations we use two general operations, push and pull. Push inserts X elements into level X^3/2, and pull removes the X elements with smallest keys from level X^3/2 and returns them in sorted order. An INSERT or a DELETEMIN is performed simply by performing a push or pull on the smallest level c.

Push. To push X elements into level X^3/2, we first sort the X elements cache-obliviously using O(1+XBlogM/BXB) $O (1 + \frac{X}{B} \log_{M / B} \frac{X}{B})$ memory transfers. Next we distribute the elements in the sorted list into the down buffers of level X^3/2 by scanning through the list and simultaneously visiting the down buffers in (linked) order. More precisely, we append elements to the end of the current down buffer dX3/2i $d_{i}^{X^{3 / 2}}$ , and advance to the next down buffer as soon as we encounter an element with larger key than the pivot of . Elements with larger keys than the pivot of the last down buffer are inserted in the up buffer u^{X^3/2}. Scanning through the X elements take O(1+XB) $O (1 + \frac{X}{B})$ memory transfers. Even though we do not scan through every down buffer, we might perform at least one memory transfer for each of the X^1/2 possible buffers. Thus the total cost of distributing the X elements is O(XB+X1/2) $O (\frac{X}{B} + X^{1 / 2})$ memory transfers.

During the distribution of elements a down buffer may run full, that is, contain 2X elements. In this case, we split the buffer into two down buffers each containing X elements using O(1+XB) $O (1 + \frac{X}{B})$ transfers. We place the new buffer in any free down buffer location for the level and update the linked list accordingly. If the level already has the maximum number X^1/2 of down buffers, we remove the last down buffer d^X_X^1/2 by inserting its no more than 2X elements into the up buffer using O(1+XB) $O (1 + \frac{X}{B})$ memory transfers. Since X elements must have been inserted since the last time the buffer split, the amortized splitting cost per element is O(1X+1B) $O (\frac{1}{X} + \frac{1}{B})$ transfers. In total, the amortized number of memory transfers used on splitting buffers while distributing the X elements is O(1+XB) $O (1 + \frac{X}{B})$ .

If the up buffer runs full during the above process, that is, contains more than X^3/2 elements, we recursively push all of these elements into the next level up. Note that after such a recursive push, X^3/2 elements have to be inserted (pushed) into the up buffer of level X^3/2 before another recursive push is needed.

Overall we can perform a push of X elements from level X into level X^3/2 in O(X1/2+XBlogM/BXB) $O (X^{1 / 2} + \frac{X}{B} \log_{M / B} \frac{X}{B})$ memory transfers amortized, not counting the cost of any recursive push operations; it is easy to see that a push maintains all three invariants.

Pull. To describe how to pull the X smallest keys elements from level X^3/2, we first assume that the down buffers contain at least 32X $\frac{3}{2} X$ elements. In this case the first three down buffers , , and contain the between 32X $\frac{3}{2} X$ and 6X smallest elements (Invariants 4 and 5). We find and remove the X smallest elements simply by sorting these elements using O(1+XBlogM/BXB) $O (1 + \frac{X}{B} \log_{M / B} \frac{X}{B})$ memory transfers. The remaining between X/2 and 5X elements are left in one, two, or three down buffers containing between X/2 and 2X elements each. These buffers can easily be constructed in O(1+XB) $O (1 + \frac{X}{B})$ transfers. Thus we use O(1+XBlogM/BXB) $O (1 + \frac{X}{B} \log_{M / B} \frac{X}{B})$ memory transfers in total. It is easy to see that Invariants 4–6 are maintained.

In the case where the down buffers contain fewer than 32X $\frac{3}{2} X$ elements, we first pull the X^3/2 elements with smallest keys from the next level up. Because these elements do not necessarily have smaller keys than the, say U, elements in the up buffer u^{X^3/2}, we then sort this up buffer and merge the two sorted lists. Then we insert the U elements with largest keys into the up buffer, and distribute the remaining between X^3/2 and X3/2+32X $X^{3 / 2} + \frac{3}{2} X$ elements into X^1/2 down buffers containing between X and X+32X1/2 $X + \frac{3}{2} X^{1 / 2}$ each (such that the O(1X+1B) $O (\frac{1}{X} + \frac{1}{B})$ amortized down buffer split bound is maintained). It is easy to see that this maintains the three invariants. Afterwards, we can find the X minimal key elements as above. Note that after a recursive pull, X^3/2 elements have to be deleted (pulled) from the down buffers of level X^3/2 before another recursive pull is needed. Note also that a pull on level X^3/2 does not affect the number of elements in the up buffer u^{X^3/2}. Since we distribute elements into the down and up buffers after a recursive pull using one sort and one scan of X^3/2 elements, the cost of doing so is dominated by the cost of the recursive pull operation itself. Thus ignoring the cost of recursive pulls, we have shown that a pull of X elements from level X^3/2 down to level X can be performed in O(1+XBlogM/BXB) $O (1 + \frac{X}{B} \log_{M / B} \frac{X}{B})$ memory transfers amortized, while maintaining Invariants 4–6.

35.4.2.4Analysis

To analyze the amortized cost of an INSERT or DELETEMIN operation, we consider the total number of memory transfers used to perform push and pull operations during N2 $\frac{N}{2}$ operations; to ensure that the structure always consists of O(log log N) levels and use O(N) space we rebuild it using O(NBlogM/BNB) $O (\frac{N}{B} \log_{M / B} \frac{N}{B})$ memory transfers (or O(1BlogM/BNB) $O (\frac{1}{B} \log_{M / B} \frac{N}{B})$ transfers per operation) after every N2 $\frac{N}{2}$ operations [14].

The total cost of N2 $\frac{N}{2}$ such operations is analyzed as follows: We charge a push of X elements from level X up to level X^3/2 to level X. Since X elements have to be inserted in the up buffer uX of level X between such pushes, and as elements can only be inserted in uX when elements are inserted (pushed) into level X, O(N/X) pushes are charged to level X during the N2 $\frac{N}{2}$ operations. Similarly, we charge a pull of X elements from level X^3/2 down to level X to level X. Since between such pulls Θ(X) elements have to be deleted from the down buffers of level X by pulls on X, O(N/X) pulls are charged to level X during the N2 $\frac{N}{2}$ operations.

Above we argued that a push or pull charged to level X uses O(X1/2+XBlogM/BXB) $O (X^{1 / 2} + \frac{X}{B} \log_{M / B} \frac{X}{B})$ memory transfers. We can reduce this cost to O(XBlogM/BXB) $O (\frac{X}{B} \log_{M / B} \frac{X}{B})$ by more carefully examining the costs for differently sized levels. First consider a push or pull of X ≥ B2 elements into or from level X^3/2 ≥ B3. In this case XB≥X−−√ $\frac{X}{B} \geq \sqrt{X}$ , and we trivially have that O(X1/2+XBlogM/BXB)=O(XBlogM/BXB) $O (X^{1 / 2} + \frac{X}{B} \log_{M / B} \frac{X}{B}) = O (\frac{X}{B} \log_{M / B} \frac{X}{B})$ . Next, consider the case B^4/3 ≤ X < B2, where the X^1/2 term in the push bound can dominate and we have to analyze the cost of a push more carefully. In this case we are working on a level X^3/2 where B2 ≤ X^3/2 < B3; there is only one such level. Recall that the X^1/2 cost was from distributing X sorted elements into the less than X^1/2 down buffers of level X^3/2. More precisely, a block of each buffer may have to be loaded and written back without transferring a full block of elements into the buffer. Assuming M = Ω(B2), we from X^1/2 ≤ B see that a block for each of the buffers can fit into fast memory. Consequently, if a fraction of the fast memory is used to keep a partially filled block of each buffer of level X^3/2 (B2 ≤ X^3/2 ≤ B3) in fast memory at all times, and full blocks are written to disk, the X^1/2 cost would be eliminated. In addition, if all of the levels of size less than B2 (of total size O(B2)) are also kept in fast memory, all transfer costs associated with them would be eliminated. The optimal paging strategy is able to keep the relevant blocks in fast memory at all times and thus eliminates these costs.

Finally, since each of the O(N/X) push and pull operations charged to level X (X > B2) uses O(XBlogM/BXB) $O (\frac{X}{B} \log_{M / B} \frac{X}{B})$ amortized memory transfers, the total amortized transfer cost of an INSERT or DELETEMIN operation in the sequence of N2 $\frac{N}{2}$ such operations is

O (\sum i = 0 \infty 1 B log M / B N ( 2 / 3 ) i B) = O (1 B log M / B N B) .

$O (\sum_{i = 0}^{\infty} \frac{1}{B} \log_{M / B} \frac{N^{(2 / 3)^{i}}}{B}) = O (\frac{1}{B} \log_{M / B} \frac{N}{B}) .$

Theorem 35.7

Using Θ(M) fast memory, N INSERT, DELETEMIN, and DELETE operations can be performed on an initially empty exponential level priority queue using O(N) space in O(1BlogM/BNB) $O (\frac{1}{B} \log_{M / B} \frac{N}{B})$ amortized memory transfers each.

35.52d Orthogonal Range Searching

As discussed in Section 35.3, there exist cache-oblivious B-trees that support updates and queries in O(log_B N) memory transfers (e.g., Theorem 35.5); several cache-oblivious B-tree variants can also support (one-dimensional) range queries in O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ memory transfers [6,8,9], but at an increased amortized update cost of O(logBN+log2NB)=O(log2BN) $O (\log_{B} N + \frac{\log^{2} N}{B}) = O (\log_{B}^{2} N)$ memory transfers (e.g., Theorem 35.4).

In this section we discuss cache-oblivious data structures for two-dimensional orthogonal range searching, that is, structures for storing a set of N points in the plane such that the points in a axis-parallel query rectangle can be reported efficiently. In Section 35.5.1 we first discuss a cache-oblivious version of a kd-tree. This structure uses linear space and answers queries in O(N/B−−−−√+KB) $O (\sqrt{N / B} + \frac{K}{B})$ memory transfers; this is optimal among linear space structures [24]. It supports updates in O(logNB⋅logM/BN)=O(log2BN) $O (\frac{\log N}{B} \cdot \log_{M / B} N) = O (\log_{B}^{2} N)$ transfers. In Section 35.5.2 we then discuss a cache-oblivious version of a two-dimensional range tree. The structure answers queries in the optimal O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ memory transfers but uses O(N log2N) space. Both structures were first described by Agarwal et al. [11].

35.5.1Cache-Oblivious kd-Tree

35.5.1.1Structure

The cache-oblivious kd-tree is simply a normal kd-tree laid out in memory using the van Emde Boas layout. This structure, proposed by Bentley [25], is a binary tree of height O(log N) with the N points stored in the leaves of the tree. The internal nodes represent a recursive decomposition of the plane by means of axis-orthogonal lines that partition the set of points into two subsets of equal size. On even levels of the tree the dividing lines are horizontal, and on odd levels they are vertical. In this way a rectangular region R_v is naturally associated with each node v, and the nodes on any particular level of the tree partition the plane into disjoint regions. In particular, the regions associated with the leaves represent a partition of the plane into rectangular regions containing one point each. Refer to Figure 35.12.

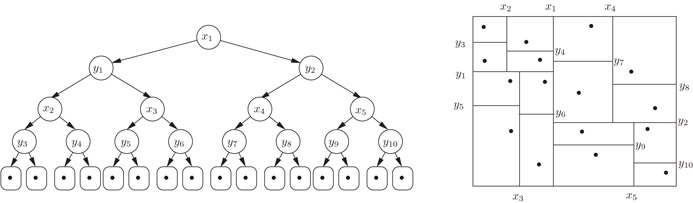
Figure 35.12kd-tree and the corresponding partitioning.

35.5.1.2Query

An orthogonal range query Q on a kd-tree T $T$ is answered recursively starting at the root: At a node v we advance the query to a child v_c of v if Q intersects the region R_{v_c} associated with v_c. At a leaf w we return the point in w if it is contained in Q. A standard argument shows that the number of nodes in T $T$ visited when answering Q, or equivalently, the number of nodes v where R_v intersects Q, is O(N−−√+K) $O (\sqrt{N} + K)$ ; N−−√ $\sqrt{N}$ nodes v are visited where R_v is intersected by the boundary of Q and K nodes u with R_u completely contained in Q [25].

If the kd-tree T $T$ is laid out using the van Emde Boas layout, we can bound the number of memory transfers used to answer a query by considering the nodes log B levels above the leaves of T $T$ . There are O(NB) $O (\frac{N}{B})$ such nodes as the subtree Tv $T_{v}$ rooted in one such node v contains B leaves. By the standard query argument, the number of these nodes visited by a query is O(N/B−−−−√+KB) $O (\sqrt{N / B} + \frac{K}{B})$ . Thus, the number of memory transfers used to visit nodes more than log B levels above the leaves is O(N/B−−−−√+KB) $O (\sqrt{N / B} + \frac{K}{B})$ . This is also the overall number of memory transfers used to answer a query, since (as argued in Section 35.2.1) the nodes in Tv $T_{v}$ are contained in O(1) blocks, that is, any traversal of (any subset of) the nodes in a subtree Tv $T_{v}$ can be performed in O(1) memory transfers.

35.5.1.3Construction

In the RAM model, a kd-tree on N points can be constructed recursively in O(N log N) time; the root dividing line is found using an O(N) time median algorithm, the points are distributed into two sets according to this line in O(N) time, and the two subtrees are constructed recursively. Since median finding and distribution can be performed cache-obliviously in O(N/B) memory transfers [4,5], a cache-oblivious kd-tree can be constructed in O(NBlogN) $O (\frac{N}{B} \log N)$ memory transfers. Agarwal et al. [11] showed how to construct logN−−√=12logN $\log \sqrt{N} = \frac{1}{2} \log N$ levels in O(Sort_{M, B}(N)) memory transfers, leading to a recursive construction algorithms using only O(Sort_{M, B}(N)) memory transfers.

35.5.1.4Updates

In the RAM model a kd-tree T $T$ can relatively easily be modified to support deletions in O(log N) time using global rebuilding. To delete a point from T $T$ , we simply find the relevant leaf w in O(log N) time and remove it. We then remove w’s parent and connect w’s grandparent to w’s sibling. The resulting tree is no longer a kd-tree but it still answers queries in O(N−−√+T) $O (\sqrt{N} + T)$ time, since the standard argument still applies. To ensure that N is proportional to the actual number of points in T $T$ , the structure is completely rebuilt after N2 $\frac{N}{2}$ deletions. Insertions can be supported in O(log2N) time using the so-called logarithmic method [26], that is, by maintaining log N kd-trees where the i’th kd-tree is either empty or of size 2i and then rebuilding a carefully chosen set of these structures when performing an insertion.

Deletes in a cache-oblivious kd-tree is basically done as in the RAM version. However, to still be able to load a subtree Tv $T_{v}$ with B leaves in O(1) memory transfers and obtain the O(N/B−−−−√+KB) $O (\sqrt{N / B} + \frac{K}{B})$ query bound, data locality needs to be carefully maintained. By laying out the kd-tree using (a slightly relaxed version of) the exponential layout (Section 35.3.2) rather than the van Emde Boas layout, and by periodically rebuilding parts of this layout, Agarwal et al. [11] showed how to perform a delete in O(log_B N) memory transfers amortized while maintaining locality. They also showed how a slightly modified version of the logarithmic method and the O(Sort_{M, B}(N)) construction algorithms can be used to perform inserts in O(logNBlogM/BN)=O(log2BN) $O (\frac{\log N}{B} \log_{M / B} N) = O (\log_{B}^{2} N)$ memory transfers amortized.

Theorem 35.8

There exists a cache-oblivious (kd-tree) data structure for storing a set of N points in the plane using linear space, such that an orthogonal range query can be answered in O(N/B−−−−√+KB) $O (\sqrt{N / B} + \frac{K}{B})$ memory transfers. The structure can be constructed cache-obliviously in O(Sort_{M, B}(N)) memory transfers and supports updates in O(logNBlogM/BN)=O(log2BN) $O (\frac{\log N}{B} \log_{M / B} N) = O (\log_{B}^{2} N)$ memory transfers.

35.5.2Cache-Oblivious Range Tree

The main part of the cache-oblivious range tree structure for answering (four-sided) orthogonal range queries is a structure for answering three-sided queries Q = [x_l, x_r] × [y_b,∞), that is, for finding all points with x-coordinates in the interval [x_l, x_r] and y-coordinates above y_b. Below we discuss the two structures separately.

35.5.2.1Three-Sided Queries

35.5.2.1.1Structure

Consider dividing the plane into N−−√ $\sqrt{N}$ vertical slabs X1,X2,…,XN√ $X_{1}, X_{2}, \dots, X_{\sqrt{N}}$ containing N−−√ $\sqrt{N}$ points each. Using these slabs we define 2N−−√−1 $2 \sqrt{N} - 1$ buckets. A bucket is a rectangular region of the plane that completely spans one or more consecutive slabs and is unbounded in the positive y-direction, like a three-sided query. To define the 2N−−√−1 $2 \sqrt{N} - 1$ buckets we start with N−−√ $\sqrt{N}$ active buckets b1,b2,…,bN√ $b_{1}, b_{2}, \dots, b_{\sqrt{N}}$ corresponding to the N−−√ $\sqrt{N}$ slabs. The x-range of the slabs define a natural linear ordering on these buckets. We then imagine sweeping a horizontal sweep line from y = − ∞ to y = ∞. Every time the total number of points above the sweep line in two adjacent active buckets, b_i and b_j, in the linear order falls to N−−√ $\sqrt{N}$ , we mark b_i and b_j as inactive. Then we construct a new active bucket spanning the slabs spanned by b_i and b_j with a bottom y-boundary equal to the current position of the sweep line. This bucket replaces b_i and b_j in the linear ordering of active buckets. The total number of buckets defined in this way is 2N−−√−1 $2 \sqrt{N} - 1$ , since we start with N−−√ $\sqrt{N}$ buckets and the number of active buckets decreases by one every time a new bucket is constructed. Note that the procedure defines an active y-interval for each bucket in a natural way. Buckets overlap but the set of buckets with active y-intervals containing a given y-value (the buckets active when the sweep line was at that value) are non-overlapping and span all the slabs. This means that the active y-intervals of buckets spanning a given slab are non-overlapping. Refer to Figure 35.13a.

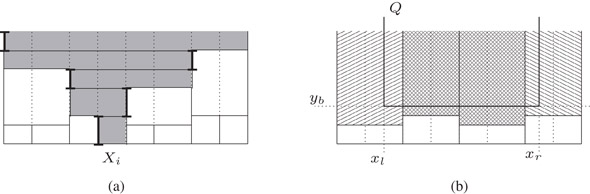
Figure 35.13(a) Active intervals of buckets spanning slab X_i; (b) Buckets active at y_b.

After defining the 2N−−√−1 $2 \sqrt{N} - 1$ buckets, we are ready to present the three-sided query data structure; it is defined recursively: It consists of a cache-oblivious B-tree T $T$ on the N−−√ $\sqrt{N}$ boundaries defining the N−−√ $\sqrt{N}$ slabs, as well as a cache-oblivious B-tree for each of the N−−√ $\sqrt{N}$ slabs; the tree Ti $T_{i}$ for slab i contains the bottom endpoint of the active y-intervals of the O(N−−√) $O (\sqrt{N})$ buckets spanning the slab. For each bucket b_i we also store the N−−√ $\sqrt{N}$ points in b_i in a list Bi $B_{i}$ sorted by y-coordinate. Finally, recursive structures S1,S2,…,S2N√−1 $S_{1}, S_{2}, \dots, S_{2 \sqrt{N} - 1}$ are built on the N−−√ $\sqrt{N}$ points in each of the 2N−−√−1 $2 \sqrt{N} - 1$ buckets.

35.5.2.1.2Layout

The layout of the structure in memory consists of O(N) memory locations containing T $T$ , then T1,…,TN√ $T_{1}, \dots, T_{\sqrt{N}}$ , and B1,…,B2N√−1 $B_{1}, \dots, B_{2 \sqrt{N} - 1}$ , followed by the recursive structures S1,…,S2N√−1 $S_{1}, \dots, S_{2 \sqrt{N} - 1}$ . Thus the total space use of the structure is S(N)≤2N−−√⋅S(N−−√)+O(N)=O(NlogN) $S (N) \leq 2 \sqrt{N} \cdot S (\sqrt{N}) + O (N) = O (N \log N)$ .

35.5.2.1.3Query

To answer a three-sided query Q, we consider the buckets whose active y-interval contain y_b. These buckets are non-overlapping and together they contain all points in Q, since they span all slabs and have bottom y-boundary below y_b. We report all points that satisfy Q in each of the buckets with x-range completely between x_l and x_r. At most two other buckets b_l and b_r—the ones containing x_l and x_r—can contain points in Q, and we find these points recursively by advancing the query to Sl $S_{l}$ and Sr $S_{r}$ . Refer to Figure 35.13b.

We find the buckets b_l and b_r that need to be queried recursively and report the points in the completely spanned buckets as follows. We first query T $T$ using O(logBN−−√) $O (\log_{B} \sqrt{N})$ memory transfers to find the slab X_l containing x_l. Then we query Tl $T_{l}$ using another O(logBN−−√) $O (\log_{B} \sqrt{N})$ memory transfers to find the bucket b_l with active y-interval containing y_b. We can similarly find b_r in O(logBN−−√) $O (\log_{B} \sqrt{N})$ memory transfers. If b_l spans slabs X_l, X_{l + 1},…, X_m we then query Tm+1 $T_{m + 1}$ with y_b in O(logBN−−√) $O (\log_{B} \sqrt{N})$ memory transfers to find the active bucket b_i to the right of b_l completely spanned by Q (if it exists). We report the relevant points in b_i by scanning Bi $B_{i}$ top-down until we encounter a point not contained in Q. If K′ is the number or reported points, a scan of Bi $B_{i}$ takes O(1+K′B) $O (1 + \frac{K^{'}}{B})$ memory transfers. We continue this procedure for each of the completely spanned active buckets. By construction, we know that every two adjacent such buckets contain at least N−−√ $\sqrt{N}$ points above y_b. First consider the part of the query that takes place on recursive levels of size N ≥ B2, such that N−−√/B≥logBN−−√≥1 $\sqrt{N} / B \geq \log_{B} \sqrt{N} \geq 1$ . In this case the O(logBN−−√) $O (\log_{B} \sqrt{N})$ overhead in finding and processing two consecutive completely spanned buckets is smaller than the O(N−−√/B) $O (\sqrt{N} / B)$ memory transfers used to report output points; thus we spend O(logBN−−√+KiB) $O (\log_{B} \sqrt{N} + \frac{K_{i}}{B})$ memory transfers altogether to answer a query, not counting the recursive queries. Since we perform at most two queries on each level of the recursion (in the active buckets containing x_l and x_r), the total cost over all levels of size at least B2 is O(∑loglogBNi=1logBN1/2i+KiB)=O(logBN+KB) $O (\sum_{i = 1}^{\log \log_{B} N} \log_{B} N^{1 / 2^{i}} + \frac{K_{i}}{B}) = O (\log_{B} N + \frac{K}{B})$ transfers. Next consider the case where N = B. In this case the whole level, that is, T $T$ , T1,…,TB√ $T_{1}, \dots, T_{\sqrt{B}}$ and B1,…,B2B√−1 $B_{1}, \dots, B_{2 \sqrt{B} - 1}$ , is stored in O(B) contiguously memory memory locations and can thus be loaded in O(1) memory transfers. Thus the optimal paging strategy can ensure that we only spend O(1) transfers on answering a query. In the case where N≤B−−√ $N \leq \sqrt{B}$ , the level and all levels of recursion below it occupies O(B−−√logB−−√)=O(B) $O (\sqrt{B} \log \sqrt{B}) = O (B)$ space. Thus the optimal paging strategy can load it and all relevant lower levels in O(1) memory transfers. This means that overall we answer a query in O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ memory transfers, provided that N and B are such that we have a level of size B2 (and thus of size B and B−−√ $\sqrt{B}$ ); when answering a query on a level of size between B and B2 we cannot charge the O(logBN−−√) $O (\log_{B} \sqrt{N})$ cost of visiting two active consecutive buckets to the ( < B) points found in the two buckets. Agarwal et al. [11] showed how to guarantee that we have a level of size B2 by assuming that B = 2^2d for some non-negative integer d. Using a somewhat different construction, Arge et al. [27] showed how to remove this assumption.

Theorem 35.9

There exists a cache-oblivious data structure for storing N points in the plane using O(N log N) space, such that a three-sided orthogonal range query can be answered in O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ memory transfers.

35.5.2.2Four-sided queries

Using the structure for three-sided queries, we can construct a cache-oblivious range tree structure for four-sided orthogonal range queries in a standard way. The structure consists of a cache-oblivious B-tree T $T$ on the N points sorted by x-coordinates. With each internal node v we associate a secondary structure for answering three-sided queries on the points stored in the leaves of the subtree rooted at v: If v is the left child of its parent then we have a three-sided structure for answering queries with the opening to the right, and if v is the right child then we have a three-sided structure for answering queries with the opening to the left. The secondary structures on each level of the tree use O(N log N) space, for a total space usage of O(N log2N).

To answer an orthogonal range query Q, we search down T $T$ using O(log_B N) memory transfers to find the first node v where the left and right x-coordinate of Q are contained in different children of v. Then we query the right opening secondary structure of the left child of v, and the left opening secondary structure of the right child of v, using O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ memory transfers. Refer to Figure 35.14. It is easy to see that this correctly reports all K points in Q.

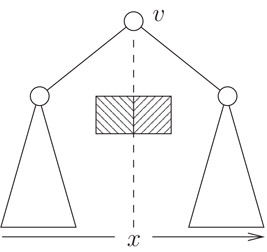
Figure 35.14Answering a four-sided query in v using two three-sided queries in v’s children.

Theorem 35.10

There exists a cache-oblivious data structure for storing N points in the plane using O(N log2N) space, such that an orthogonal range query can be answered in O(logBN+KB) $O (\log_{B} N + \frac{K}{B})$ memory transfers.

Acknowledgments

Lars Arge was supported in part by the National Science Foundation through ITR grant EIA–0112849, RI grant EIA–9972879, CAREER grant CCR–9984099, and U.S.–Germany Cooperative Research Program grant INT–0129182.

Gerth Stølting Brodal was supported by the Carlsberg Foundation (contract number ANS-0257/20), BRICS (Basic Research in Computer Science, www.brics.dk, funded by the Danish National Research Foundation), and the Future and Emerging Technologies programme of the EU under contract number IST-1999-14186 (ALCOM-FT).

Rolf Fagerberg was supported by BRICS (Basic Research in Computer Science, www.brics.dk, funded by the Danish National Research Foundation), and the Future and Emerging Technologies programme of the EU under contract number IST-1999-14186 (ALCOM-FT). Part of this work was done while at University of Aarhus.

References

1.A. Aggarwal and J. S. Vitter. The input/output complexity of sorting and related problems. Communications of the ACM, 31(9):1116–1127, Sept. 1988.

2.L. Arge. External memory data structures. In J. Abello, P. M. Pardalos, and M. G. C. Resende, editors, Handbook of Massive Data Sets, pages 313–358. Kluwer Academic Publishers, 2002.

3.J. S. Vitter. External memory algorithms and data structures: Dealing with massive data. ACM Computing Surveys, 33(2):209–271, June 2001.

4.M. Frigo, C. E. Leiserson, H. Prokop, and S. Ramachandran. Cache-oblivious algorithms. In Proc. 40th Annual IEEE Symposium on Foundations of Computer Science, pages 285–298. IEEE Computer Society Press, 1999.

5.H. Prokop. Cache-oblivious algorithms. Master’s thesis, Massachusetts Institute of Technology, Cambridge, MA, June 1999.

6.M. A. Bender, E. D. Demaine, and M. Farach-Colton. Cache-oblivious B-trees. In Proc. 41st Annual IEEE Symposium on Foundations of Computer Science, pages 339–409. IEEE Computer Society Press, 2000.

7.M. A. Bender, R. Cole, and R. Raman. Exponential structures for cache-oblivious algorithms. In Proc. 29th International Colloquium on Automata, Languages, and Programming, volume 2380 of Lecture Notes in Computer Science, pages 195–207. Springer, 2002.

8.M. A. Bender, Z. Duan, J. Iacono, and J. Wu. A locality-preserving cache-oblivious dynamic dictionary. In Proc. 13th Annual ACM-SIAM Symposium on Discrete Algorithms, pages 29–38. SIAM, 2002.

9.G. S. Brodal, R. Fagerberg, and R. Jacob. Cache oblivious search trees via binary trees of small height. In Proc. 13th Annual ACM-SIAM Symposium on Discrete Algorithms, pages 39–48. SIAM, 2002.

10.N. Rahman, R. Cole, and R. Raman. Optimized predecessor data structures for internal memory. In Proc. 3rd Workshop on Algorithm Engineering, volume 2141 of Lecture Notes in Computer Science, pages 67–78. Springer, 2001.

11.P. K. Agarwal, L. Arge, A. Danner, and B. Holland-Minkley. Cache-oblivious data structures for orthogonal range searching. In Proc. 19th ACM Symposium on Computational Geometry, pages 237–245. ACM Press, 2003.

12.G. S. Brodal and R. Fagerberg. Cache oblivious distribution sweeping. In Proc. 29th International Colloquium on Automata, Languages, and Programming, volume 2380 of Lecture Notes in Computer Science, pages 426–438. Springer, 2002.

13.M. Bender, E. Demaine, and M. Farach-Colton. Efficient tree layout in a multilevel memory hierarchy. In Proc. 10th Annual European Symposium on Algorithms, volume 2461 of Lecture Notes in Computer Science, pages 165–173. Springer, 2002. Full version at http://www.cs.sunysb.edu/bender/pub/treelayout-full.ps.

14.L. Arge, M. Bender, E. Demaine, B. Holland-Minkley, and J. I. Munro. Cache-oblivious priority-queue and graph algorithms. In Proc. 34th ACM Symposium on Theory of Computation, pages 268–276. ACM Press, 2002.

15.G. S. Brodal and R. Fagerberg. Funnel heap - a cache oblivious priority queue. In Proc. 13th International Symposium on Algorithms and Computation, volume 2518 of Lecture Notes in Computer Science, pages 219–228. Springer, 2002.

16.G. S. Brodal, R. Fagerberg, and K. Vinther. Engineering a cache-oblivious sorting algorithm. In Proc. 6th Workshop on Algorithm Engineering and Experiments, 2004.

17.R. E. Ladner, R. Fortna, and B.-H. Nguyen. A comparison of cache aware and cache oblivious static search trees using program instrumentation. In Experimental Algorithmics, From Algorithm Design to Robust and Efficient Software (Dagstuhl seminar, September 2000), volume 2547 of Lecture Notes in Computer Science, pages 78–92. Springer, 2002.

18.R. Bayer and E. McCreight. Organization and maintenance of large ordered indexes. Acta Informatica, 1:173–189, 1972.

19.P. van Emde Boas. Preserving order in a forest in less than logarithmic time and linear space. Information Processing Letters, 6:80–82, 1977.

20.M. A. Bender, G. S. Brodal, R. Fagerberg, D. Ge, S. He, H. Hu, J. Iacono, and A. López-Ortiz. The cost of cache-oblivious searching. In Proc. 44th Annual IEEE Symposium on Foundations of Computer Science, pages 271–282. IEEE Computer Society Press, 2003.

21.G. S. Brodal and R. Fagerberg. On the limits of cache-obliviousness. In Proc. 35th ACM Symposium on Theory of Computation, pages 307–315. ACM Press, 2003.

22.A. Andersson and T. W. Lai. Fast updating of well-balanced trees. In Proc. 2nd Scandinavian Workshop on Algorithm Theory, volume 447 of Lecture Notes in Computer Science, pages 111–121. Springer, 1990.

23.A. Itai, A. G. Konheim, and M. Rodeh. A sparse table implementation of priority queues. In Proc. 8th International Colloquium on Automata, Languages, and Programming, volume 115 of Lecture Notes in Computer Science, pages 417–431. Springer, 1981.

24.K. V. R. Kanth and A. K. Singh. Optimal dynamic range searching in non-replicating index structures. In Proc. International Conference on Database Theory, volume 1540 of Lecture Notes in Computer Science, pages 257–276. Springer, 1999.

25.J. L. Bentley. Multidimensional binary search trees used for associative searching. Communication of the ACM, 18:509–517, 1975.

26.J. L. Bentley. Decomposable searching problems. Information Processing Letters, 8(5):244–251, 1979.

27.L. Arge, G. S. Brodal, and R. Fagerberg. Improved cache-oblivious two-dimensional orthogonal range searching. Unpublished results, 2004.

^*This chapter has been reprinted from first edition of this Handbook, without any content updates.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 35. Cache Oblivious Data Structures

Create new playlist

Sign In

Sign Up

Table of Contents for
35. Cache Oblivious Data Structures