CHAPTER 34
Pricing Interest Rate Swaps
Aims
- To show that cash flows in a swap are equivalent to a replication portfolio consisting of a position in a fixed rate bond and a floating rate note (bond) (FRN).
- To demonstrate that the swap rate is calculated by assuming that the swap must have the same value to both parties at inception – otherwise the swap would not take place. The swap rate is determined solely by the term structure of interest rates.
- To show how arbitrage arguments can be invoked to demonstrate that the market value of an FRN is equal to the notional principal Q in the FRN (a) at inception
 , and (b) just after, any reset date
, and (b) just after, any reset date 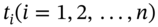 .
. - To show how to value an FRN at any date
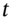 (between payment dates), using two different methods the ‘short method’ and the ‘forward rate method’. Both methods give the same outcome for the value of the FRN at any date
(between payment dates), using two different methods the ‘short method’ and the ‘forward rate method’. Both methods give the same outcome for the value of the FRN at any date 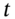 .
. - To show that the value of a swap at any date
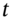 is the difference between the present value of the cash flows from a fixed rate bond and the present value of the cash flows from an FRN.
is the difference between the present value of the cash flows from a fixed rate bond and the present value of the cash flows from an FRN. - To analyse how the mark-to-market value of a swap changes through time in response to changes in interest rates and the number of remaining payments in the swap.
A swap can be priced by considering the swap as a synthetic bond portfolio. When a pay-fixed, receive-float interest rate swap is initiated (at ![]() ) each leg of the swap must have the same (present) value – otherwise both sides would not enter into the swap. This insight allows us to price the swap (i.e. determine the fixed swap rate,
) each leg of the swap must have the same (present) value – otherwise both sides would not enter into the swap. This insight allows us to price the swap (i.e. determine the fixed swap rate, ![]() ).
).
Over time ![]() the (mark-to-market) value of the swap to any one party can be positive or negative, as the present value (PV) of the fixed and floating rate payments in the swap alter as interest rates change. Somewhat paradoxically the PV of the variable rate (LIBOR) payments remain relatively stable, even though these floating cash flows change over time. So it is the fixed leg of the swap which is the main source of changes in the mark-to-market value of the swap.
the (mark-to-market) value of the swap to any one party can be positive or negative, as the present value (PV) of the fixed and floating rate payments in the swap alter as interest rates change. Somewhat paradoxically the PV of the variable rate (LIBOR) payments remain relatively stable, even though these floating cash flows change over time. So it is the fixed leg of the swap which is the main source of changes in the mark-to-market value of the swap.
34.1 CASH FLOWS IN A SWAP
The payments in a receive-float, pay-fixed swap are shown in Figure 34.1 and look exactly like a long position in an FRN and a short position in a fixed rate bond.
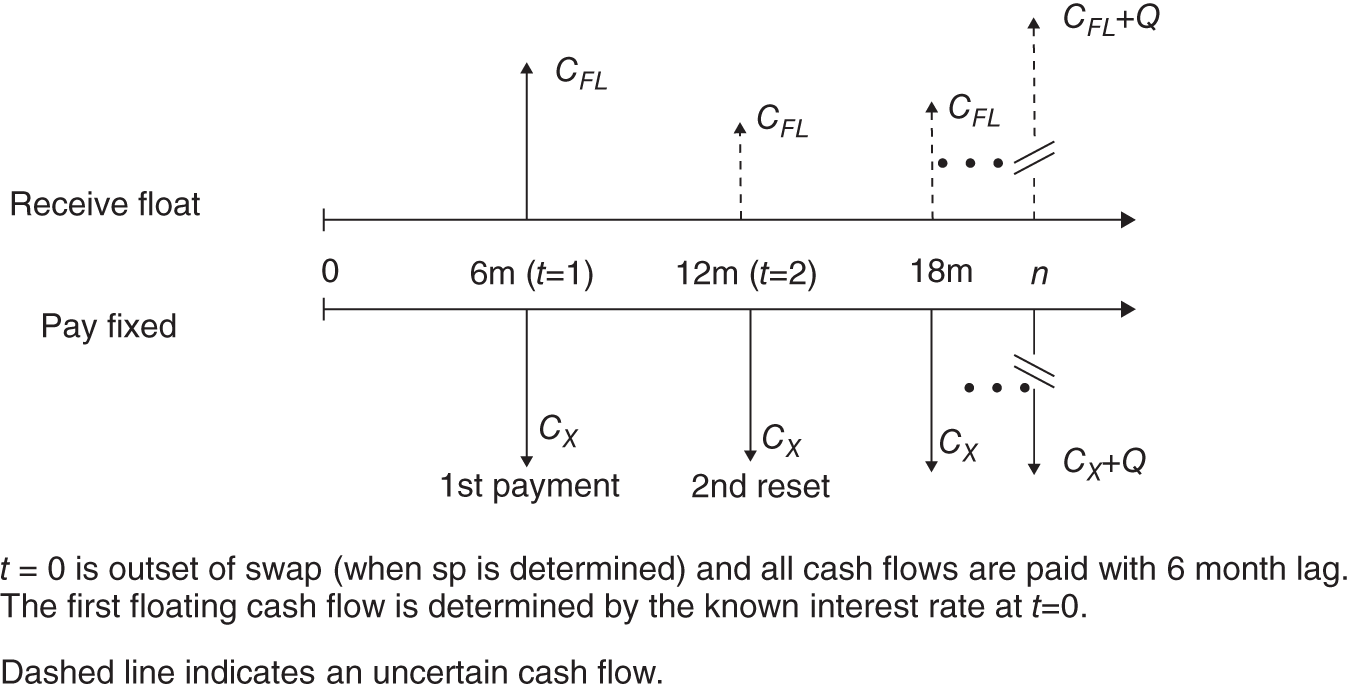
FIGURE 34.1 Cash flows in a receive-float, pay-fixed swap
If you have a ‘receive-float, pay-fixed’ swap, on a nominal principal ![]() , your net cash receipts at each 6-month payment date, are
, your net cash receipts at each 6-month payment date, are ![]() . These are the same cash flows that would ensue from selling a fixed rate bond with maturity value1 $100m and using the proceeds to purchase (i.e. go long) a floating rate bond (also with maturity value $100m). Both the floating and fixed rate bond are redeemed at maturity for
. These are the same cash flows that would ensue from selling a fixed rate bond with maturity value1 $100m and using the proceeds to purchase (i.e. go long) a floating rate bond (also with maturity value $100m). Both the floating and fixed rate bond are redeemed at maturity for ![]() . In an interest rate swap the notional principal
. In an interest rate swap the notional principal ![]() is not exchanged at maturity, so there are no cash flows from this source in the swap. But the latter is also the case if we are long the FRN and short the fixed rate bond since the two principal amounts of $Q at maturity, cancel out (Figure 34.1). Hence, the net payment in the swap and the net payment from the long-short bond position are both
is not exchanged at maturity, so there are no cash flows from this source in the swap. But the latter is also the case if we are long the FRN and short the fixed rate bond since the two principal amounts of $Q at maturity, cancel out (Figure 34.1). Hence, the net payment in the swap and the net payment from the long-short bond position are both ![]() at maturity.
at maturity.
The replication portfolio of being long an FRN and short a fixed rate bond (both with maturity value Q) gives exactly the same (net) cash flows as the swap. You would not enter the swap unless the present value of floating payments ![]() equals the present value of the fixed payments
equals the present value of the fixed payments ![]() . Hence you only enter the swap if at
. Hence you only enter the swap if at ![]() ,
, ![]() . As we see below, this result allows us to determine the swap rate. However, first we consider how to value the FRN.
. As we see below, this result allows us to determine the swap rate. However, first we consider how to value the FRN.
34.2 FLOATING RATE NOTE (FRN)
An FRN is a bond with variable rate coupons based on future LIBOR rates. We can value the FRN in a number of different ways:
- Using arbitrage arguments.
- Using all forward rates to estimate all (expected) future floating cash flows. The value of the FRN is then the present value of these expected cash flows. This is the ‘forward rate method’.
- Using a ‘short method’ to value the FRN which only uses the floating cash flow at the next payment date and the known principal
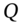 of the FRN.
of the FRN.
Not surprisingly, all three methods give the same answer for the value of the FRN (at any date) and all the methods are equivalent, although it is the arbitrage argument which really underlies the other two approaches.
It is also important to be clear about what point in time you are trying to value the FRN. When pricing a swap you need to find the value of the FRN at inception of the swap ![]() . We will see that the present value of the FRN at
. We will see that the present value of the FRN at ![]() is just the principal in the FRN, which equals
is just the principal in the FRN, which equals ![]() . After inception of the swap, interest rates may change (i.e. the yield curve will shift) and the market value of the FRN could increase or decrease – but we can still use the above three methods to value the FRN at
. After inception of the swap, interest rates may change (i.e. the yield curve will shift) and the market value of the FRN could increase or decrease – but we can still use the above three methods to value the FRN at ![]() .
.
34.2.1 Value of an FRN at t = 0
An FRN is a bond whose floating (coupon) payments are adjusted in line with prevailing market interest rates, which are determined at the previous reset date. Consider a notional principle of ![]() and a LIBOR rate of
and a LIBOR rate of ![]() at time
at time ![]() . At
. At ![]() the coupon payable at the first reset date
the coupon payable at the first reset date ![]() , on the floating rate bond is known and equals
, on the floating rate bond is known and equals ![]() (where
(where ![]() ). Subsequent coupon payments on the ‘floater’ depend on future LIBOR rates at
). Subsequent coupon payments on the ‘floater’ depend on future LIBOR rates at ![]() which are not known at
which are not known at ![]() . However, somewhat counter-intuitively it is shown in Appendix 34 that even though these future floating payments are uncertain, nevertheless the following propositions are true:
. However, somewhat counter-intuitively it is shown in Appendix 34 that even though these future floating payments are uncertain, nevertheless the following propositions are true:
Proposition 1
At inception
, all future receipts on an FRN have a present value equal to Q
Proposition 2
Immediately after any reset date
, all future floating receipts have a present value of Q
Proposition 1 allows us to price the swap at inception, ![]() . Proposition 2 helps in valuing the FRN (and hence the swap) after inception (i.e.
. Proposition 2 helps in valuing the FRN (and hence the swap) after inception (i.e. ![]() ). Hence the value of an FRN over time is like the stylised pattern in Figure 34.2 – its value equals
). Hence the value of an FRN over time is like the stylised pattern in Figure 34.2 – its value equals ![]() at
at ![]() , it also equals
, it also equals ![]() just after any of the reset dates and at the maturity date,
just after any of the reset dates and at the maturity date, ![]() . Between reset dates, the market value of the FRN can deviate from its notional value
. Between reset dates, the market value of the FRN can deviate from its notional value ![]() (Figure 34.2). But as interest rates generally do not change drastically over short periods, the value of the FRN does not deviate too far from
(Figure 34.2). But as interest rates generally do not change drastically over short periods, the value of the FRN does not deviate too far from ![]() , between reset dates.
, between reset dates.
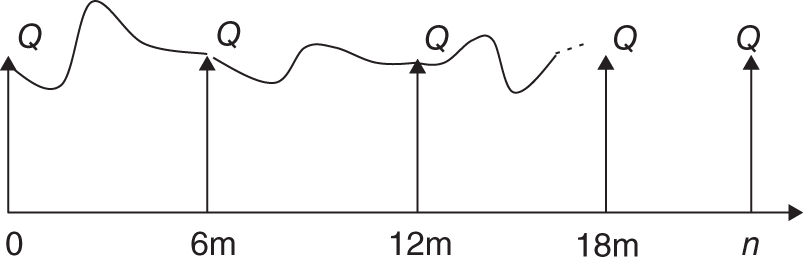
FIGURE 34.2 Value of a FRN over time
A semi-intuitive way of showing that the (present) value of an FRN equals ![]() at
at ![]() and just after each payment date is to value the FRN using current forward rates and to recursively calculate its value, as we move back in time from the final payment date (Figure 34.3).
and just after each payment date is to value the FRN using current forward rates and to recursively calculate its value, as we move back in time from the final payment date (Figure 34.3).
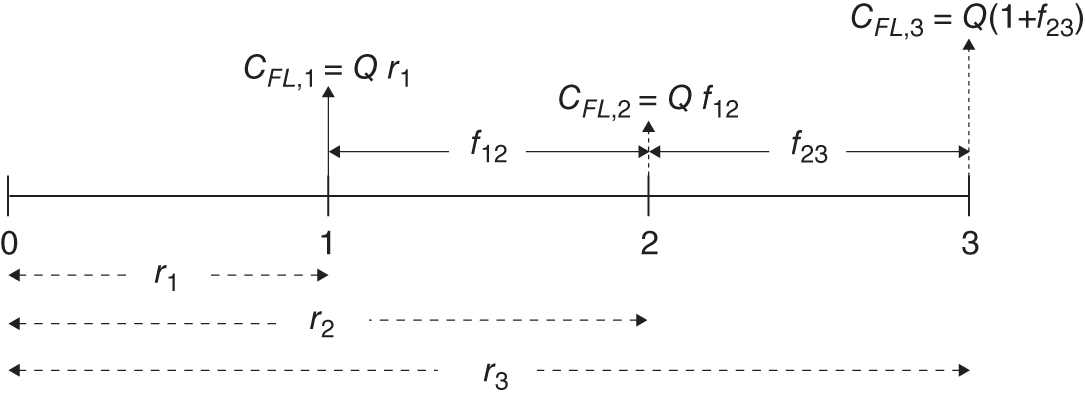
FIGURE 34.3 FRN, expected cash flows
For simplicity consider a 3-period FRN, which pays annual coupons (and we use compound rates). The forward rates are all known at ![]() . (They are calculated from the known spot rates at
. (They are calculated from the known spot rates at ![]() ). The expected final floating payment is
). The expected final floating payment is ![]() but this has an expected present value at
but this has an expected present value at![]() of
of ![]() . Hence at
. Hence at ![]() , the present value of the cash flow at
, the present value of the cash flow at ![]() plus the cash flow at
plus the cash flow at ![]() is
is ![]() – the latter has a present value at
– the latter has a present value at ![]() of
of ![]() . We have now shown that at
. We have now shown that at ![]() , the present value of both the future cash flows at
, the present value of both the future cash flows at ![]() and
and ![]() are worth
are worth ![]() in total. At
in total. At ![]() we also receive a cash flow
we also receive a cash flow ![]() , so at
, so at ![]() all (current and future) cash flows are worth
all (current and future) cash flows are worth ![]() – but these have a present value at
– but these have a present value at ![]() of
of ![]() . Hence the value of all the future cash flows
. Hence the value of all the future cash flows ![]() from the FRN have a value today (at
from the FRN have a value today (at ![]() ) of
) of ![]() . Also note from the above that just after the floating rate payment dates at
. Also note from the above that just after the floating rate payment dates at ![]() and
and ![]() , the (present) value of any remaining future cash flows, is also equal to
, the (present) value of any remaining future cash flows, is also equal to ![]() . (See Appendix 34 for a formal proof of this using arbitrage arguments.)
. (See Appendix 34 for a formal proof of this using arbitrage arguments.)
34.3 PRICING A SWAP: SHORT METHOD
To price a plain vanilla swap at the outset ![]() means finding the fixed rate
means finding the fixed rate ![]() which makes the (present) value of the fixed rate bond equal to the (present) value of the FRN – or what is the same thing, that the fixed-for-floating swap has zero initial value.
which makes the (present) value of the fixed rate bond equal to the (present) value of the FRN – or what is the same thing, that the fixed-for-floating swap has zero initial value.
For example, suppose you are a swap dealer who has to fix the swap rate ![]() for a ‘new’ fixed for floating (LIBOR) swap with a notional principal of
for a ‘new’ fixed for floating (LIBOR) swap with a notional principal of ![]() . Let
. Let ![]() be the payment each period in the fixed leg of the swap and
be the payment each period in the fixed leg of the swap and ![]() the tenor in the fixed-leg (e.g. 180/360 or 181/360 etc.). The discount factors are
the tenor in the fixed-leg (e.g. 180/360 or 181/360 etc.). The discount factors are ![]() where
where ![]() and
and ![]() is the actual number of days from
is the actual number of days from ![]() to
to ![]() .2 The (present) value of the fixed leg at
.2 The (present) value of the fixed leg at ![]() is:
is:
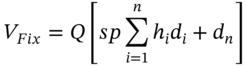
Note that if the notional principal in the swap is $1, then the term in square brackets is the ‘present value of the fixed payments in an interest rate swap, with $1 notional principal’. Now we make use of our above proposition that the market value at ![]() of all the future floating (LIBOR) cash flows are today equal to the notional principal, so
of all the future floating (LIBOR) cash flows are today equal to the notional principal, so ![]() . The swap rate is that value of
. The swap rate is that value of ![]() for which
for which ![]() . Hence the swap rate is the solution to:
. Hence the swap rate is the solution to:
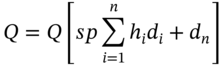
The swap rate depends only on the term structure of spot rates at ![]() (and not on
(and not on ![]() ):
):
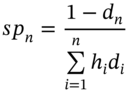
This is the swap rate for an n-period swap. There are different quoted swap rates for swaps with different maturities. The ‘swap spread’ is often defined as the difference between the swap rate and the yield to maturity (![]() ) of an n-period government bond, so the ‘swap spread’ =
) of an n-period government bond, so the ‘swap spread’ = ![]() . A plot of the swap rate
. A plot of the swap rate ![]() against
against ![]() is often referred to as the ‘swap rate curve’.
is often referred to as the ‘swap rate curve’.
Swap rates generally lie slightly above T-bond yields because swap rates reflect the creditworthiness of major banks that provide swaps (and also reflect liquidity in the market). In fact swap rates rather than government bond rates are often used as benchmark rates for pricing assets such as corporate bonds, mortgages etc., because the swaps' market is so liquid and virtually risk free. If the tenor ![]() in the fixed leg of the swap is constant, then
in the fixed leg of the swap is constant, then
Table 34.1 shows the calculation of the (4-year) swap rate ![]() p.a. from the spot yield curve on 15 March-01, using the above formula (with
p.a. from the spot yield curve on 15 March-01, using the above formula (with ![]() for all periods in the fixed-leg of the swap).3
for all periods in the fixed-leg of the swap).3
TABLE 34.1 Calculation of swap rate
| Today is 15 March-01 | ||||||||
| Notional principal: 100,000 | ||||||||
| Days in year (swap convention): 360 | ||||||||
| Days to 1st floating reset date: 184 | ||||||||
| 6-month LIBOR on 15 March-01: 5.15% | ||||||||
| Date | Days | Cum. days | Spot rates LIBOR | Discount factors LIBOR | Forward rates LIBOR | Floating cash flows | PV (Floating cash flows) | d*f*m |
| 15-Mar-01 | ||||||||
| 15-Sep-01 | 184 | 184 | 5.15 | 0.9744 | 5.1500 | 2,632.2222 | 2,564.7133 | 0.0256 |
| 15-Mar-02 | 181 | 365 | 5.27 | 0.9493 | 5.2537 | 2,641.4436 | 2,507.4648 | 0.0251 |
| 15-Sep-02 | 184 | 549 | 5.36 | 0.9244 | 5.2576 | 2,687.2221 | 2,484.1663 | 0.0248 |
| 15-Mar-03 | 181 | 730 | 5.45 | 0.9005 | 5.2905 | 2,659.9635 | 2,395.2546 | 0.0240 |
| 15-Sep-03 | 184 | 914 | 5.54 | 0.8767 | 5.3102 | 2,714.1088 | 2,379.4313 | 0.0238 |
| 15-Mar-04 | 182 | 1096 | 5.65 | 0.8532 | 5.4376 | 102,749.0067 | 87,668.9698 | 0.0235 |
| 1. Swap rate | 0.0536 | 2. Swap rate | 0.0536 | |||||
| PV fixed CF | 100,000 | PV floating CF | 100,000 | |||||
The discount rates are calculated as follows. For example, between 15 March-01 and 15 September-02 ![]() there are 549 days and the quoted spot rate (at
there are 549 days and the quoted spot rate (at ![]() ) is
) is ![]() p.a., so the discount factor is:
p.a., so the discount factor is:
How can we check that ![]() is the correct swap rate? The PV of the fixed cash flows using
is the correct swap rate? The PV of the fixed cash flows using ![]() should equal the notional principal in the swap of $100,000. We have
should equal the notional principal in the swap of $100,000. We have ![]() (payable every 6 months) and using the discount factors in Table 34.1:
(payable every 6 months) and using the discount factors in Table 34.1:
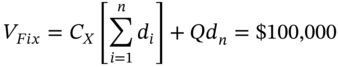
So, using ![]() ensures that
ensures that ![]() which is as expected. If the swap dealer is a fixed rate receiver (and floating rate payer) she will set the actual swap rate above 5.3579% to reflect the transactions cost of hedging her swaps book and the credit risk of the counterparty in the swap.
which is as expected. If the swap dealer is a fixed rate receiver (and floating rate payer) she will set the actual swap rate above 5.3579% to reflect the transactions cost of hedging her swaps book and the credit risk of the counterparty in the swap.
34.4 PRICING A SWAP: FORWARD RATE METHOD
When using the ‘forward rate method’ to determine the swap rate we use all the forward rates to determine the present value of the floating rate payments ![]() , set this equal to the present value of the fixed rate payments
, set this equal to the present value of the fixed rate payments ![]() and then solve for the unknown swap rate,
and then solve for the unknown swap rate, ![]() . Of course, we already know that the present value of the floating payments is equal to
. Of course, we already know that the present value of the floating payments is equal to ![]() but the ‘forward rate method’ is useful in pricing other kinds of swap which we meet later – so we introduce the method here.
but the ‘forward rate method’ is useful in pricing other kinds of swap which we meet later – so we introduce the method here.
The floating coupon payments are ![]() where the forward rates
where the forward rates ![]() apply to the period between
apply to the period between ![]() . Therefore
. Therefore ![]() is actually the known LIBOR rate fixed at
is actually the known LIBOR rate fixed at ![]() for the period
for the period ![]() . Also
. Also ![]() and
and ![]() = actual number of days between each repayment date. Spot rates are used to calculate forward rates. For example, the forward rate
= actual number of days between each repayment date. Spot rates are used to calculate forward rates. For example, the forward rate ![]() applicable to the period
applicable to the period ![]() is derived from the two spot rates
is derived from the two spot rates ![]() ,
, ![]() using the arbitrage relationship:
using the arbitrage relationship:
For example, from Table 34.1 we see that ![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() . Hence
. Hence ![]() .4 The present value of all the floating payments,
.4 The present value of all the floating payments, ![]() at
at ![]() is:
is:
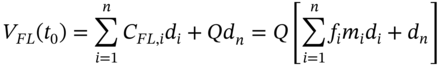
and from Table 34.2 this gives ![]() as expected, since we already know that at inception of the swap, the value of the floating leg equals
as expected, since we already know that at inception of the swap, the value of the floating leg equals ![]() . The PV of the fixed cash flows is
. The PV of the fixed cash flows is ![]() hence, as before:
hence, as before:
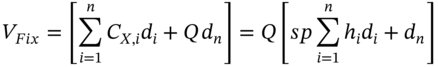
TABLE 34.2 New spot rates and discount factors
| Today is 15 June-01 | |||||||||
| Notional principal: 100,000 | |||||||||
| Days in year (swap convention): 360 | |||||||||
| Days to 1st floating reset date: 184 | |||||||||
| 6-month LIBOR on 15 March-01: 5.15% | |||||||||
| Swap rate (set on 15 March-01): 5.36% | |||||||||
| Date | Days | Cum. days | New LIBOR rate 15 Jun-01 | Discount factors LIBOR | Fixed CF, sp = 0.0536 | PV fixed cash flows | PV (floating cash flows) | Floating coupons | PV floating cash flows |
| 15-Jun-01 | |||||||||
| 15-Sep-01 | 92 | 92 | 6.15 | 0.9845 | 2,679 | 2,637 | 5.1500 | 2,632 | 2,591 |
| 15-Mar-02 | 181 | 273 | 6.27 | 0.9546 | 2,679 | 2,557 | 6.2330 | 3,134 | 2,992 |
| 15-Sep-02 | 184 | 457 | 6.36 | 0.9253 | 2,679 | 2,479 | 6.1988 | 3,168 | 2,932 |
| 15-Mar-03 | 181 | 638 | 6.45 | 0.8974 | 2,679 | 2,404 | 6.1784 | 3,106 | 2,788 |
| 15-Sep-03 | 184 | 822 | 6.54 | 0.8701 | 2,679 | 2,331 | 6.1492 | 3,143 | 2,735 |
| 15-Mar-04 | 182 | 1004 | 6.65 | 0.8436 | 102,679 | 86,615 | 6.2182 | 3,144 | 87,007 |
| PV fixed CF | 99,024 | PV floating CF | 101,044 | ||||||
| Value ‘receive-float, pay-fixed’ swap (15 June) | 2,020 | ||||||||
Equating![]() and
and ![]() and rearranging, we obtain an expression for the swap rate using the ‘forward rate method’:
and rearranging, we obtain an expression for the swap rate using the ‘forward rate method’:
The swap rate calculated using (34.11) is shown as ‘2. Swap rate’ in Table 34.1 and naturally it gives the same numerical value of 5.36% as that derived in Equation (34.5), which uses only the term structure of spot (or discount) rates.
34.5 MARKET VALUE OF A SWAP
At inception of the swap on 15 March-01, the value of the swap is ![]() by construction. We now want to calculate the mark-to-market value of the swap sometime after its inception. The value of the swap changes over time as interest rates change and as the number of cash flows remaining changes. The value of a receive-float pay-fixed swap at
by construction. We now want to calculate the mark-to-market value of the swap sometime after its inception. The value of the swap changes over time as interest rates change and as the number of cash flows remaining changes. The value of a receive-float pay-fixed swap at ![]() is the difference between the value of the FRN (floating leg) and the fixed coupon bond:
is the difference between the value of the FRN (floating leg) and the fixed coupon bond:
Suppose on 15 June (i.e. after 3 months), spot rates (and hence forward rates) have all increased – what is the new value of the swap? To value the swap we need to find the new (present) values of the FRN and the fixed-rate bond, using the new higher spot rates. We begin by valuing the FRN and we can use two different methods:
- ‘short method’ – use only the next LIBOR cash flow (plus Q)
- ‘forward rate method’ – use forward rates as forecasts of all future LIBOR cash flows.
34.5.1 Value of FRN at t > 0 (‘Short Method’)
Suppose we are trying to value the swap at t (15 June), between ![]() (15 March) and
(15 March) and ![]() (15 September-01) – Figure 34.4. From our earlier analysis we know that the present value of the floating leg equals Q immediately after any payment date. Between payment dates an FRN can have a value different to Q.
(15 September-01) – Figure 34.4. From our earlier analysis we know that the present value of the floating leg equals Q immediately after any payment date. Between payment dates an FRN can have a value different to Q.
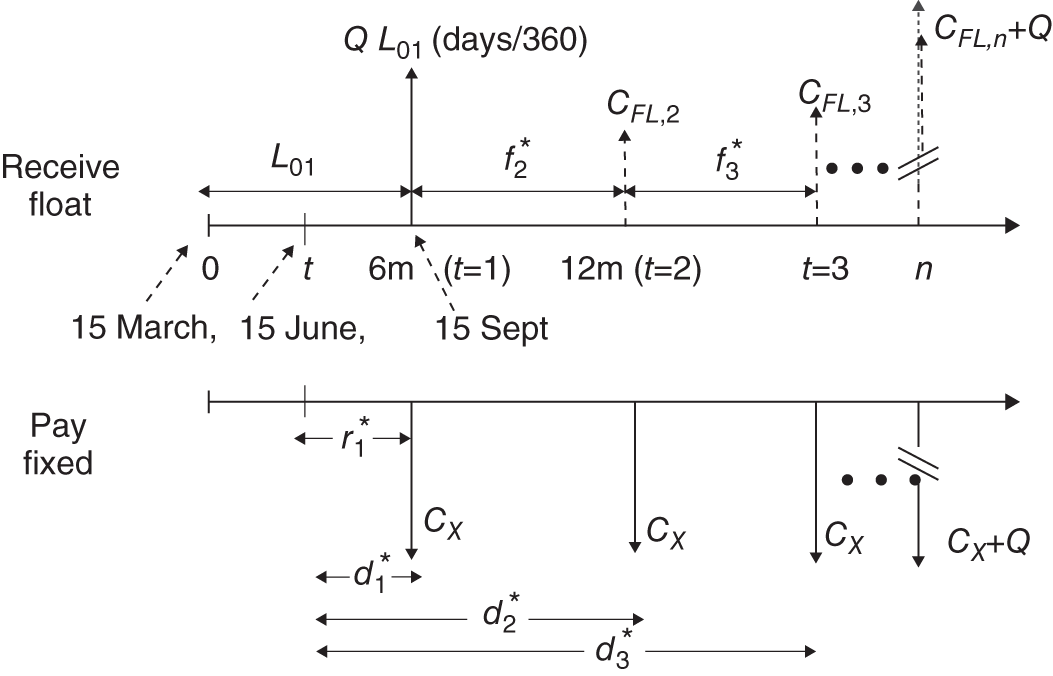
FIGURE 34.4 Value of swap at t, receive-float, pay-fixed
The floating cash flow at ![]() (15 September) is known and depends on the LIBOR rate
(15 September) is known and depends on the LIBOR rate ![]() which was fixed on 15 March (at
which was fixed on 15 March (at ![]() and which pays out at
and which pays out at ![]() ). This cash flow is:
). This cash flow is:
Using proposition 2, the value of all future LIBOR cash flows accruing after![]() (that is
(that is ![]() plus the final payment of Q at
plus the final payment of Q at ![]() ), have a PV at
), have a PV at![]() of Q. Hence the value of the FRN at
of Q. Hence the value of the FRN at ![]() depends only on the present value of the next floating LIBOR payment
depends only on the present value of the next floating LIBOR payment ![]() plus Q. The new spot rate applicable from 15 June to 15 September (92 days) is
plus Q. The new spot rate applicable from 15 June to 15 September (92 days) is ![]() , so the new discount rate
, so the new discount rate ![]() (Table 34.2).
(Table 34.2).
Hence the (present) value of the FRN on 15 June is:
At inception of the swap (15 March) the present value of the floating rate payments was $100,000. Although the spot-LIBOR rate ![]() has increased and the next cash flow of $2,632 is unchanged, nevertheless the value of the FRN on 15 June has increased. This is because you now have less time to wait (92 days) for the first payment on 15 September (compared with 184 days at inception of the swap on 15 March-01).
has increased and the next cash flow of $2,632 is unchanged, nevertheless the value of the FRN on 15 June has increased. This is because you now have less time to wait (92 days) for the first payment on 15 September (compared with 184 days at inception of the swap on 15 March-01).
The above formula with minor changes in notation applies to the value of the FRN between any two payment dates – its value depends only on the present value of the next known floating LIBOR payment ![]() , plus Q.
, plus Q.
34.5.2 Value of FRN at t > 0 (‘Forward Rate Method’)
The value of the FRN at t (15 June) is the PV of all future LIBOR cash flows after time t. We can value the FRN by using the new forward rates at ![]() to provide an estimate of expected future cash flows and discount these cash flows back to time
to provide an estimate of expected future cash flows and discount these cash flows back to time ![]() , using the new spot rates determined at
, using the new spot rates determined at ![]() . This is the ‘forward rate method’.
. This is the ‘forward rate method’.
The value of the FRN between inception and the first payment date (![]() ) depends on: (i) the PV of the next LIBOR payment
) depends on: (i) the PV of the next LIBOR payment ![]() which was fixed at
which was fixed at ![]() ; plus (ii) PV of all the future floating rate payments
; plus (ii) PV of all the future floating rate payments ![]() at payment dates
at payment dates ![]() (
(![]() ); plus (iii) the PV of Q. The ‘new’ interest rates at
); plus (iii) the PV of Q. The ‘new’ interest rates at ![]() are higher (Table 34.2) than at
are higher (Table 34.2) than at ![]() . All spot rates are now measured from time
. All spot rates are now measured from time ![]() and hence we have ‘new’ discount factors and new forward rates:
and hence we have ‘new’ discount factors and new forward rates:
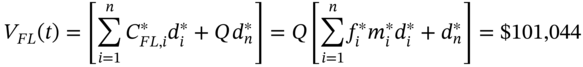
where ![]()
![]() , so the discount factors apply to the period from today
, so the discount factors apply to the period from today ![]() to the remaining payment dates,
to the remaining payment dates, ![]() . The PV of the FRN on 15 June is
. The PV of the FRN on 15 June is ![]() – not surprisingly this is the same value as found above using the ‘short method’.
– not surprisingly this is the same value as found above using the ‘short method’.
For more ‘exotic’ swaps than the plain vanilla swap considered here (and discussed in Chapter 35), we often cannot use the ‘short method’ and we need to value the floating leg using ‘the forward rate method’.
34.5.3 Value of Fixed Leg at t > 0
Now let's value the fixed leg at t. The fixed payments are ![]() . The only change to note is that discount rates now use the new spot rates at time t so that
. The only change to note is that discount rates now use the new spot rates at time t so that ![]() where
where ![]() is the actual number of days from
is the actual number of days from ![]() to
to ![]() , that is from 15 June to the other reset dates (Figure 34.4), hence:
, that is from 15 June to the other reset dates (Figure 34.4), hence:
The value of the fixed leg on 15 June-01 is calculated in Table 34.2:
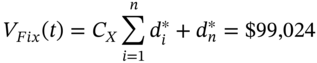
The PV of the fixed leg has fallen from $100,000 (at inception on 15 March) to $99,024 (on 15 June) because of the rise in spot rates which alters the discount factors ![]() . The value of a receive-float, pay-fixed swap at time t is therefore:
. The value of a receive-float, pay-fixed swap at time t is therefore:
The rise in interest rates between 15 March and 15 June results in an increase in value of the receive-floating LIBOR-leg of the swap and a fall in the value of the ‘pay-fixed’ leg of the swap – so the ‘receive-float pay-fixed swap’ has increased in value and is worth $2,020.
34.6 SWAP DELTA AND PVBP
In the above example the value of the swap changed because of (i) a change in the yield curve and (ii) because we moved through time and revalued the swap on 15 June. If we had valued the swap on, say, 15 April two years later and interest rates had not changed, the swap value would have changed simply because it has only two further cash flows remaining.
It is useful when hedging a swap to separate out the effect of interest rate changes and the ‘passage of time’, on the market value of the swap. To do so we consider what happens to the (present) value of the swap when all interest rates increase by the same small amount over a small time interval (say one day). If the change in interest rates is taken to be 1 bp then the resulting change in the value of the swap is known as the swap delta. The latter concept is useful when hedging a position in swaps – which we discuss in Chapter 39. The swap delta is a similar concept to the delta of an option. The value of the swap on 15 June (using the ‘short method’) gives:
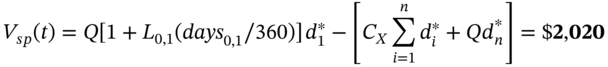
where
What will happen to the value of the swap if all interest rates rise by 1 bp, over the next day? Higher spot and hence forward rates lead to an increase in the expected cash flows from the FRN and no change in the cash flows in the fixed leg, hence the net cash receipts of the receive-float pay-fixed swap, increase. But does this imply that the present value of these net cash flows increases?
All future floating LIBOR payments (except that at the next payment date) will increase but so will the discount rates applied to these higher floating cash flows, and in present value terms these two effects are largely offsetting so the value of the floating leg of the swap does not vary much (see Figure 34.2). But how much is this offset? Using the ‘short method’ we can easily see what's happening to the value of the FRN:
If interest rates increase, ![]() will fall the next day but not by much, as it only falls because of the increase in the (single) short-term LIBOR interest rate which implies
will fall the next day but not by much, as it only falls because of the increase in the (single) short-term LIBOR interest rate which implies ![]() is smaller. On the other hand, although the fixed dollar payments each period do not change, there may be many of these, so their present value falls by a relatively large amount, after a rise in all spot interest rates. But as a fixed rate payer you are better off when the PV of your ‘debt’ is lower. Hence:
is smaller. On the other hand, although the fixed dollar payments each period do not change, there may be many of these, so their present value falls by a relatively large amount, after a rise in all spot interest rates. But as a fixed rate payer you are better off when the PV of your ‘debt’ is lower. Hence:
A rise in interest rates will increase the present value of a ‘receive-float, pay-fixed’ swap.
Hence, a ‘receive-float, pay-fixed swap’ has a positive delta.
Another way of seeing how the value of a long maturity ‘receive-float pay-fixed’ swap changes after a rise in interest rates is to note that the floating-leg (FRN) has a small duration ![]() and the fixed-leg has a large duration,
and the fixed-leg has a large duration, ![]() . For each leg of the swap we have
. For each leg of the swap we have ![]() , hence for a parallel shift in the yield curve:
, hence for a parallel shift in the yield curve:
Since ![]() then a rise in interest rates (usually) increases the value of the receive-float pay-fixed swap.
then a rise in interest rates (usually) increases the value of the receive-float pay-fixed swap.
34.7 SUMMARY
- A plain vanilla interest rate swap involves one party exchanging a series of fixed cash flows for cash flows determined by a floating rate (LIBOR). The notional principal in the swap is not exchanged.
- Cash flows in a ‘receive-float, pay-fixed swap’ are equivalent to taking a long position in an FRN and a short position in a fixed rate bond. At inception, the two parties in the swap will not enter the swap unless the value of the fixed bond equals the value of the floating bond. Hence the swap rate is calculated by making the fixed leg of the swap equal to the value of the floating leg, at inception of the swap.
- The swap rate is determined by the term structure of spot rates, at inception of the swap.
- After a swap has been initiated, the value of the swap may become positive or negative (to one of the parties). The mark-to-market value of a swap at any time is the present value of the remaining future net cash flows in the swap.
- The mark-to-market value of a swap changes over time as spot interest rates (and hence forward rates) change and because the swap will have less cash flows outstanding. For a long-dated swap, it is the fixed-leg rather than the floating-leg whose present value changes by a large amount, as interest rates change.
- The change in the (present) value of a swap position after a 1 basis point change in all interest rates is known as the swap delta (or the present value of a basis point, PVBP). The swap delta is a useful concept when swap dealers try to hedge the whole of their swaps book.
APPENDIX 34: VALUE OF AN FRN USING ARBITRAGE
We wish to determine the present value ![]() of all future floating rate payments on an FRN at any reset date
of all future floating rate payments on an FRN at any reset date ![]() (
(![]() ). The FRN has a notional (face) value Q, which is fixed. Using an arbitrage argument, we show that
). The FRN has a notional (face) value Q, which is fixed. Using an arbitrage argument, we show that ![]() must equal Q immediately after any reset date, including at
must equal Q immediately after any reset date, including at ![]() when the swap is initiated. (Note that this analysis says nothing about the value of the FRN when we are between reset/payment dates.)
when the swap is initiated. (Note that this analysis says nothing about the value of the FRN when we are between reset/payment dates.)
Suppose that immediately after any reset/payment date ![]() we have
we have ![]() . Consider the following arbitrage strategy:
. Consider the following arbitrage strategy:
- Sell (short) an FRN at
 and invest
and invest  at LIBOR (in a risk-free bank deposit).
at LIBOR (in a risk-free bank deposit).Net cash inflow at
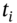 is
is 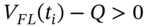 .
. - At the next payment date use the LIBOR receipts from the bank deposit to pay LIBOR on the short FRN.
Roll over the principal
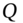 of the deposit. Repeat this process until
of the deposit. Repeat this process until  .
.Net cash inflow = 0 at each payment date up to
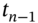 .
. - At
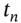 use the LIBOR interest from the deposit account to pay LIBOR on the FRN and use the principal
use the LIBOR interest from the deposit account to pay LIBOR on the FRN and use the principal 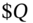 from the deposit account to pay the principal on the FRN.
from the deposit account to pay the principal on the FRN.Net cash inflow = 0.
Hence, if ![]() at any payment date (including
at any payment date (including ![]() ) there is a risk-free arbitrage profit to be made, since you receive a net cash inflow at
) there is a risk-free arbitrage profit to be made, since you receive a net cash inflow at ![]() and no net cash outflows after that date. This arbitrage strategy will result in bond arbitrageurs selling FRNs at time
and no net cash outflows after that date. This arbitrage strategy will result in bond arbitrageurs selling FRNs at time ![]() , which will push the market price of the FRN down, until its market value equals
, which will push the market price of the FRN down, until its market value equals ![]() (its par value), at which point arbitrage trades cease and equilibrium is restored. But the market price of the FRN is just the market's valuation of the future cash flows from the FRN so
(its par value), at which point arbitrage trades cease and equilibrium is restored. But the market price of the FRN is just the market's valuation of the future cash flows from the FRN so ![]() . Since the arbitrage is riskless, we expect
. Since the arbitrage is riskless, we expect ![]() at all future payment/reset dates
at all future payment/reset dates ![]() (
(![]() ), and today at
), and today at ![]() .
.
EXERCISES
Question 1
What are the main causes of a change in the mark-to-market value of a 20-year pay-fixed, receive-floating (plain vanilla) interest rate swap? Explain.
Question 2
From a swap dealer's viewpoint, explain a ‘matched’ 20-year swap.
Question 3
Today a swap dealer agrees a receive-fixed, pay-floating 10-year interest rate swap on a notional principal of $10m. What might cause the swap to have a positive value to the swap dealer, in 3 months' time? Explain.
Question 4
A swap dealer has to decide the swap rate to charge in a ‘new’ fixed-for-floating (LIBOR) swap on a notional principal of ![]() . The swap's maturity is 2 years, with payments every 180 days. The term structure of LIBOR rates is 12% p.a. over 6 months, 12.25% p.a. over 1 year, 12.75% p.a. over 18 months and 13.02% p.a. over 2 years (all continuously compounded). Assume there are 360 days in a year.
. The swap's maturity is 2 years, with payments every 180 days. The term structure of LIBOR rates is 12% p.a. over 6 months, 12.25% p.a. over 1 year, 12.75% p.a. over 18 months and 13.02% p.a. over 2 years (all continuously compounded). Assume there are 360 days in a year.
Calculate the swap rate.
Briefly explain what factors determine the quoted swap rate.
Question 5
At inception, the swap rate is ![]() (simple rate) on a plain vanilla
(simple rate) on a plain vanilla ![]() swap.
swap.
The previous reset date was 15 January. The 6-month LIBOR rate on 15 January was 3.6% p.a. (simple rate). The tenor in the swap is 6 months.
It is now 15 March. The next (LIBOR) reset date is 15 July and the swap matures on the next 15 January (in 10 months' time).
Assume 6 months equals ½ year etc. and the yield curve is ‘flat’ at 5% p.a. (continuously compounded). Forward rates to calculate floating cash flows in the swap are ‘simple rates’, not continuously compounded.
Calculate the mark-to-market value of a receive-fixed, pay-floating swap (on 15 March) by considering the swap as a series of forward contracts.
Question 6
A ![]() notional, interest rate swap has a remaining life of 10 months. Under the terms of the swap, 6-month LIBOR (floating) is exchanged for a fixed swap rate,
notional, interest rate swap has a remaining life of 10 months. Under the terms of the swap, 6-month LIBOR (floating) is exchanged for a fixed swap rate, ![]() p.a.
p.a.
The yield curve is currently ‘flat’ at 10% p.a. (continuously compounded), which is equivalent to 10.254% p.a. (simple interest).
The 6-month LIBOR rate, 2 months ago, at the previous ‘reset date’ was 9.6% p.a. (simple rate) and the next payment dates are in 4 months and 10 months.
Consider the swap as a combination of a fixed and a floating bond and calculate the current value of the swap, to the party paying floating.
Question 7
It is immediately after a payment date on swap with a notional principal of ![]() (annual payments). The swap rate
(annual payments). The swap rate ![]() . The swap is a receive-fixed, pay-floating interest rate swap with two remaining payment dates.
. The swap is a receive-fixed, pay-floating interest rate swap with two remaining payment dates.
The current spot rates for the two periods are ![]() p.a. and
p.a. and ![]() p.a., respectively and the forward rate is
p.a., respectively and the forward rate is ![]() p.a. (compound rates).
p.a. (compound rates).
Consider the swap as a bond portfolio and calculate the value of the swap to the party receiving-fixed.
NOTES
- 1 Also called the par, face, or principal value.
- 2 Note that even when the fixed payments are determined using the swap convention where
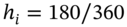 is the same for each reset period, nevertheless when calculating the discount factors
is the same for each reset period, nevertheless when calculating the discount factors 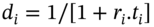 we must use the actual number of days since the swap was initiated so,
we must use the actual number of days since the swap was initiated so, 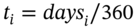 .
. - 3 As an aside note, we can use Equation (34.5) to calculate spot rates from swap rates. For example, suppose we have calculated 1-year and 2-year spot rates
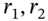 from T-bill prices then we can calculate the 3-year spot rate
from T-bill prices then we can calculate the 3-year spot rate 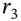 using Equation (34.5), if we observe (know) the current 3-year swap rate,
using Equation (34.5), if we observe (know) the current 3-year swap rate, 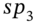 . If we also know the current market swap rates
. If we also know the current market swap rates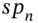 for
for 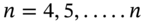 then we can use Equation (34.5) to calculate all the spot rates
then we can use Equation (34.5) to calculate all the spot rates  and hence construct the complete spot rate curve. This is often done in practice because the swaps market is very liquid and the spot rate curve is derived from observable swap rates.
and hence construct the complete spot rate curve. This is often done in practice because the swaps market is very liquid and the spot rate curve is derived from observable swap rates. - 4 Equivalently, forward rates can also be derived from the LIBOR discount rates:
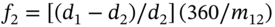 .
.