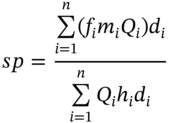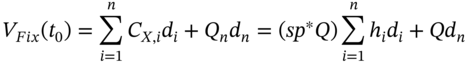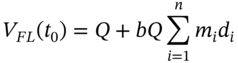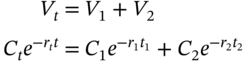CHAPTER 35
Other Interest Rate Swaps
Aims
- To price and value ‘non-standard’ interest rate swaps such as variable rate swaps, off-market swaps, zero-coupon swaps, swaps with variable notional principals and basis swaps.
- The swap rate on more complex interest rate swaps can be determined by making the present value of the fixed leg of the swap equal to the (expected) present value of the floating leg (at inception of the swap) – as for plain vanilla swaps. However, the methods used in calculating these present values differ for exotic swaps.
- To show how swap dealers hedge their interest rate swaps book using other fixed income assets such as FRAs, bonds, interest rate futures, and interest rate options.
- To demonstrate how to hedge the credit risk of a swap position using collateral, netting and credit enhancements.
35.1 SWAP DEALS
There are a wide variety of swap contracts which can be designed to suit particular customers' requirements. In a spread-to-LIBOR swap, the floating rate is not at LIBOR-flat but at LIBOR plus a spread. Since most floating-rate bank loans contain a spread over LIBOR, this swap can be constructed to exactly match the floating payments in a LIBOR bank loan. In an off-market swap, the fixed swap rate is set at whatever rate is chosen by the ‘customer’ (e.g. a corporate) – for example, this off-market swap rate might be chosen to exactly match the fixed rate on an existing bank loan. In a zero-coupon swap the fixed payment is not periodic but consists of one ‘lump sum’ payment at the maturity of the swap.
Some corporates may have fixed interest rate loans where the fixed payments change over time in a predetermined way – for example, the fixed rate might be 3% p.a. for the first 10 years followed by a fixed rate of 4% p.a. for a further 5 years. To match the payments in such a loan the corporate might use a swap to ‘receive fixed’ but the swap has a pre-agreed changing path for the (fixed) swap rate which matches that on the bank loan. Also, the corporate might pay floating (LIBOR-flat) in the swap, thus effectively converting her fixed rate loan (with different fixed rates over different time periods) to a variable rate loan.
In a basis swap both parties make floating-rate interest payments but they are linked to different floating rates, for example 90-day LIBOR against 180-day LIBOR or against the 90-day T-bill rate. This type of swap is also referred to as a floating-floating swap. It allows a corporate to exchange one set of floating-rate payments for a slightly different set of floating payments. Although LIBOR and T-bill rates (for the same maturities) tend to move together, the spread can change – which gives rise to net payments in the swap.
Another kind of basis swap is a yield curve swap. Here both parties pay floating but one might be based on a short rate (e.g. 3-month T-bill rate) and the other on the 20-year T-bond yield. If the yield curve is initially upward sloping but during the life of the swap it flattens out then this would benefit the party paying the 20-year rate and receiving the short rate.
A yield curve swap might be useful for a Savings and Loan Association (S&L) (or bank) to offset interest rate risk. An S&L has (mostly) short-term floating rate liabilities (e.g. deposits) and (some) floating rate long-term assets (e.g. variable rate mortgage receipts). The S&L will suffer if short rates rise relative to long rates (i.e. if the yield curve flattens) but it can offset this risk by entering into a yield curve swap, to receive cash flows based on a short rate and pay out cash flows based on a long rate.
Swaps may have variable notional principals. If the notional principal falls over the life of the swap this is an amortising swap. For example, if someone has floating loan payments linked to a mortgage where the principal on the ‘mortgage’ falls through time, then an amortising swap is appropriate. The converse, where the principal increases through time is known as an accreting swap. This is useful where, for example, a construction firm has building costs which increase by, say, $10m each year for 5 years and it has taken out a ‘staggered LIBOR-loan’ for $10m today, followed by an extra $10m principal in each succeeding year, over the construction period. The construction firm can convert this ‘increasing principal’ floating-rate loan into an ‘increasing principal’ fixed rate loan by entering into an accreting swap to ‘receive-floating, pay-fixed’, on a (notional) variable principal amount.
It is also possible to create a swap with a variable notional principal that first increases and then decreases over the life of the swap, to match the changing principal in a bank loan held by a corporate – this is known as a roller-coaster swap. A roller-coaster swap can be useful in hedging floating rate payments on a bank loan for project finance (e.g. for building an electricity generating station where the principal of the bank loan first increases (to pay the construction costs) and then decreases (after cash flows from the project come on stream).
Diff swaps or quanto swaps are cross-currency interest rate swaps. One party to the swap has cash flows determined by a foreign interest rate but these foreign cash flows are based on a notional principal in the home currency. They embed a fixed currency exchange rate in the swap deal.
For example, a US firm might enter a swap where it receives periodic cash flows based on (fixed) Euribor swap rates but calculated on a dollar principal amount. In the swap the US firm might pay USD-LIBOR (on the same dollar principal amount). The US firm therefore avoids any currency risk. The term ‘diff swap’ arises from the fact that payments in the swap depend on the difference between interest rates in two countries. The receipt of Euribor interest in the swap could be used to pay interest on an existing Euribor bank loan. The US firm then effectively has a fixed USD loan (and no exchange rate risk).
If you wish to enter into a swap at some time in the future at a swap rate fixed today, then a forward swap is appropriate. This is simply a forward contract on the swap rate. Now consider an option on a swap, which is known as a swaption. The swaption ‘delivers’ a (cash-market) swap at the expiration date of the option. If you choose to receive the fixed payment in the swap (and pay floating) it is called a receiver swaption. (The converse is a payer swaption.) Forward swaps and swaptions are discussed in Chapter 39.
We use the methods outlined in the previous chapter to value a variety of ‘non-standard’ interest rate swaps, these include:
- a swap with a variable notional principal
- a spread-to-LIBOR swap
- an off-market swap
- a zero-coupon swap
- a swap with a variable swap rate (for the ‘fixed’ payments).
35.2 PRICING NON-STANDARD SWAPS
35.2.1 Variable Notional Principal
Assume the day-count convention for the floating leg is 
and for the fixed leg it is 
. (We keep the subscript on 
because in some swaps 
). In amortising, accreting and roller-coaster swaps the notional principal 
varies in a pre-specified manner, determined at the outset of the swap. We can price this swap in the same way as we priced a plain vanilla interest rate swap, the only changes being:
- We replace
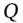with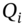 
, hence 
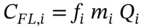and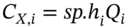 
. - We have to value the floating leg using all the forward rates – we cannot use the ‘short method’ as we have a variable notional principal
.
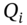At inception of the swap the value of the floating and fixed legs are:
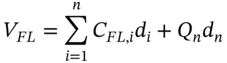
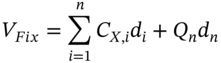
Hence equating the two present values and solving for the swap rate, 
:
Not surprisingly, the swap rate is determined by the predetermined values of the (changing) notional principal 
as well as the term structure of interest rates, reflected in 
and 
. Note that a plain vanilla swap has 
(fixed) and then (35.3) gives the swap rate for a plain vanilla swap, as derived in Chapter 34.
35.2.2 Spread-to-LIBOR Swap
Instead of LIBOR-flat in the floating leg, the swap contract may specify that the floating leg has an interest rate of 
, where 
is a spread of say 30 bps 
. We assume the notional value in the swap is fixed at 
. The value of the fixed leg is:
The floating leg can be viewed as floating payments at LIBOR-flat with a PV of 
at inception, plus periodic constant payments at 
, hence:
where we have assumed that the spread 
uses the same day-count convention as the floating payments. Equating (35.4) and (35.5), the swap rate 
, which gives zero value for the ‘spread-to-LIBOR’ swap at inception, is:
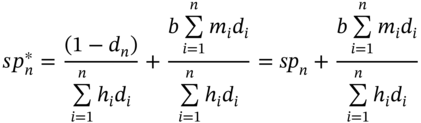
is the ‘at-market’ swap rate (at 
) for a fixed-for-floating swap at LIBOR-flat. If you are paying fixed using the ‘at-market’ swap rate 
but receiving LIBOR-flat, the value of the swap to you is zero (by construction). But if you are paying fixed at 
and receiving LIBOR+b the value of this swap to you will be positive. Hence to make the value of this ‘pay-fixed, receive-LIBOR+b’ swap equal to zero, the fixed swap rate 
you pay in this ‘spread-to-LIBOR’ swap, is greater than the ‘at-market’ swap rate 
.
35.2.3 Zero-coupon Swap (Against LIBOR-flat)
In a zero-coupon swap there is a single fixed payment of 
at 
which has present value 
. We have to determine the value for 
, which makes the swap have zero value at inception of the swap.
The floating payments are the same as in a plain vanilla swap 
, where the (notional) principal in the swap is 
. We know that the value of all these floating payments at 
is simply 
(say). Suppose 
(where 
). Equating 
we have 
. The zero-coupon swap rate (per $1 nominal principal) is then quoted as 
.
In other words, on a notional principal of $100m the fixed leg of the swap has to pay out a single payment of $117.674m at 
while the floating leg receives LIBOR on each payment date. The zero-coupon swap rate is (defined as):
It is easy to see that 
. Hence, the zero-coupon swap rate is the n-period LIBOR rate 
(p.a.) adjusted by the maturity of the swap 
.
In pricing our next set of swaps, so that the swap has the same value to both parties at inception, involves an up-front payment by one of the parties in the swap.
35.2.4 Off-market Swap (Against LIBOR-flat)
Suppose the current ‘at market’ swap rate (for an n-year swap) with 
is 
, which implies that using 
, 
, so the swap has zero value (to both parties). How do you price a swap where the fixed-rate payer wants to pay fixed at 
(every period)? This is an ‘off-market’ swap. The present value of the fixed leg at 
is:
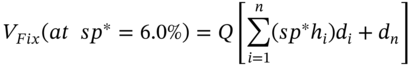
which must be less than 
. Suppose 
. Then the pay-fixed party in the off-market swap will deliver an up-front payment of 
to the swap counterparty. The ‘pay-fixed’ party in all future periods then pays fixed at 
and receives LIBOR-flat.
35.2.5 Swap with Changing Fixed Rates (Against LIBOR-flat)
It is a bit strange to think of the ‘fixed rate’ in a swap not being the same fixed rate every period. But at 
someone might like to pay a known amount each period but this predetermined amount can be different in each period.
Suppose the current ‘at market’ swap rate (for an n-year swap) with 
and with constant payments in the fixed leg is 
. The fixed payments are 
and 
– so the swap has zero value to both parties.
The known ‘fixed payments’ in the swap with a known changing value for 
are 
where each different 
at each future reset date are all known at
. The value of the fixed leg is:
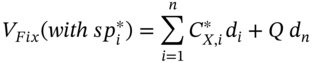
The numerical value of 
is unlikely to equal $100m and could be larger or smaller depending on the particular values chosen (at 
) for 
. Suppose 
. The ‘pay-fixed at 
would pay an up-front payment of 
at 
to the counterparty in the swap, then in all future periods would pay the (variable but) predetermined payments 
(and receive LIBOR each period).
35.2.6 Basis Swap
Consider an 18-month basis swap, with resets every 180 days, where you agree to pay the (variable) T-bill rate and receive LIBOR on a notional principal of 
. This can be replicated with two plain vanilla swaps:
Pay T-bill rate and receive-fixed + pay-fixed and receive-LIBOR
Suppose the current term structure is:
| Maturity | T-bills | LIBOR |
 |
 |
 |
 |
 |
 |
 |
 |
 |
Pricing the two plain vanilla swaps so that they have zero value at inception gives:
- Pay variable T-bill rate and receive-fixed at
:
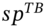(35.10a)where1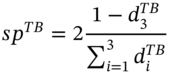
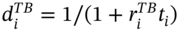
- Pay fixed at
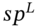and receive LIBOR
(35.10b)
The term structure of LIBOR rates is usually slightly above that for T-bills (e.g. by 20–30 bps) because the former carries more credit risk, hence we might find that 
p.a. and 
p.a. Now it is clear that the original basis swap of ‘pay the T-bill rate and receive-LIBOR’ would be priced so that one party would:
Pay the T-bill rate and receive (LIBOR – 0.4%).
35.2.7 Mark-to-market Value of Non-standard Swaps
After inception, all of the above swaps will generally have a positive or negative value to one of the parties in the swap. The mark-to-market value of these swaps can be calculated using the ‘forward rate method’. All we need to do at time 
is note the new spot rates (and hence discount rates) and calculate the new forward rates. The forward rates are used to determine the new floating rate payments 
remaining in the swap and these are discounted using the new spot rates at t, to give:
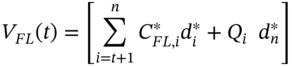
where the sum is from the next payment date 
to 
. The value of the (remaining) fixed payments at the new spot rates is straightforward:
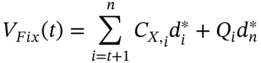
where 
. The current market value of a receive-floating, pay-fixed swap at any time after inception (
) is:
35.3 HEDGING INTEREST RATE SWAPS
A swap dealer will usually take on one side of a plain vanilla interest rate swap even if she cannot immediately find an offsetting swap. This is known as ‘warehousing’. If the dealer does warehouse an interest rate swap then she is exposed to interest rate risk. One way of hedging the floating interest payments is with a series of interest rate futures contracts. Eurodollar futures can be used and a series of Eurodollar futures is known as a Eurodollar strip.
35.3.1 Hedging Floating LIBOR Cash Flows Only
After aggregating all her interest rate swap deals, assume a swap dealer (Ms Float) currently has a net position to receive-float, pay-fixed, (in USD) which currently has positive value to the dealer. How can the swap dealer hedge against future changes in interest rates?
At first sight it may look as if she just has to hedge changes in LIBOR on the floating side since the fixed (coupon) payments are just that, fixed. Ms Float can hedge any single future LIBOR swap receipt by today, going long (buying) Eurodollar futures with a maturity date just after the LIBOR reset date. If interest rates fall in the future, Ms Float receives lower floating-rate cash flows from her swaps but the futures price will rise and the profit from closing out the futures offsets her lower LIBOR swap receipts. So today, for each LIBOR reset date in the swap Ms Float goes long 
futures:
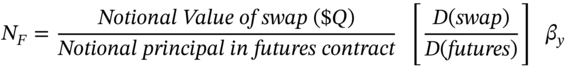
where D(swap) = ½. (say), the tenor of cash flows in the swap. If there are 
remaining reset dates, she goes long a total of 
futures contracts today, using 
contracts for each reset date – this is a strip hedge. Ms Float will then close out 
contracts at each future reset date. However, this is not the hedge usually undertaken by swaps dealers, who invariably hedge the present value of the swap.
The above is fine if you just want to hedge the future floating cash flows – so, for example, the above futures hedge is correct for a company hedging cash flows from a floating rate bank loan or bank deposit. But if the swap dealer just hedges her LIBOR floating leg of the swap she is ignoring the fixed leg. Remember that although the fixed (coupon) payments in the swap are ‘fixed’ each period, their present value is not – and above we have not yet hedged the change in the present value of the fixed payments in the swap.
35.3.2 Hedging the Mark-to-market Value
The market value of the swap changes due to (a) interest rates changes and (b) the swap has fewer payment dates remaining. We now discuss a different type of hedge where the swap dealer chooses to hedge the present value of the swap – that is, the present value of the floating receipts minus the fixed payments. If the swap dealer hedges the mark-to-market (present) value of the swap then any changes in interest rates (over a short time horizon) will not alter the present value of the swap dealer's position. Because the hedge is only effective over a short time horizon, the hedge position must be periodically rebalanced.
Hedging the PV of the swap is a conceptually different approach to hedging only the future LIBOR cash flows in the swap. The choice between these two types of hedge depends on what you consider is the most useful hedge in the circumstances. For example, it is reasonable for a company with a floating rate loan just to hedge the upcoming floating rate payments using a strip of interest rate futures contracts – since these variable loan payments are the key cash-flow risk for the corporate. But it seems more sensible for the swap dealer to hedge changes in value for both legs of the swap. If the swap currently has a value of $100m to the swap dealer, then with the hedge in place the swap dealer's position will still have $100m value, after a change in interest rates (over a short time horizon). Also for regulatory purposes it is the mark-to-market value that is used in determining how much ‘capital’ (e.g. retained profits and equity capital) the swap dealer has to hold against the ‘market risk’ of her swap's book.
Suppose you are holding a receive-float, pay-fixed swap that currently has positive value. If over the next few days all interest rates (including forward rates) fall by 1 bp (parallel shift), the mark-to-market value of your swap position will fall. It is perhaps easiest at the outset to analyse what is going on by assuming that the PV of the floating payments remains unchanged. (Remember, as interest rates change, the PV of the floating payments stays close to $Q.) As a fixed-rate payer in the swap, you are worse off after a fall in interest rates because the PV of your future fixed (coupon) payments increases – your liabilities have increased. Hence a fall in interest rates by 1 bp will result in a fall in the value of a receive-float, pay-fixed swap.
35.3.3 Delta of a Swap
The delta of a swap (by convention) is defined as the dollar change in present value of the swap for a 1 bp increase in all interest rates (i.e. an upward parallel shift in the yield curve). The present value at time t of the net cash flows at each future swap payment date 
is:
where the floating cash flow depends on the appropriate forward rate and 
is the discount factor (which depends on spot interest rates measured from today, t). The PV of the swap (with 
remaining payments) is simply the sum of these PVs:
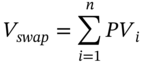
At inception the swap has zero value. Suppose the pay-fixed swap has been in existence for some time and currently has a positive market value. To calculate the swap's delta we need to find the change in the present value of the swap due to a 1 bp (per annum) increase in interest rates (over a short time horizon). To do so we calculate the new present value of the swap with all interest rates 1 bp higher (using the ‘forward rate method’ for the FRN) – this is sometimes referred to as the ‘perturbation method’.2 We therefore undertake the following steps:
- We know the current value of the swap,
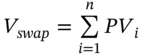. - Set ‘new’ spot rates = existing spot rates plus 1 bp.
- Calculate new discount factors,
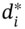and forward rates,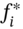 
- Calculate new floating cash flows,
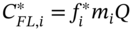at each payment date and keep the fixed cash flows 
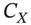unchanged. - Calculate the new net cash flows
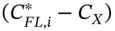. - Calculate the new PV of each net cash flow,
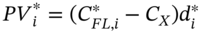using the new discount (spot) rates. - Calculate the change in PV at each payment date,
. - Calculate change in PV of all future cash flows,
.
The (dollar) change in the value of the swap 
for a 1 bp increase in all spot rates is referred to as the swap's delta (or the ‘present value of a basis point’, PVBP). A swap dealer will have a large number of interest rate swaps and it can aggregate all the fixed and floating cash flows at each payment date. The individual (net) cash flows from each swap may be positive or negative, as may their aggregated value at any payment date.
Suppose it is 15 April-01 and (to simplify matters) assume the aggregated swaps book only has payments every 6 months, with three further payments remaining. The next aggregated payments are on 15 September-01, 15 March-02, and 15 September-02. On 15 April-01 suppose the delta's for each of the three net cash flows are $10,000, $9,500, and $8,400 (Table 35.1) – giving a total swap delta of 
. Since all the deltas are positive then, if interest rates increase (fall) over the next week by 1 bp, the present value of the swap position increases (falls) by $27,900 (over the next week).3
TABLE 35.1 Hedging the PV of the swap (receive-float, pay-fixed)
| Today is 15 April-01 | |||
| Three payment dates remaining: 15 September-01, 15 March-01, 15 September-02. | |||
| 15 September-01 | 15 March-01 | 15 September-02 | |
Change in PV of net cash flows, for 1 bp change,
 |
$10,000 | $9,500 | $8,400 |
| Delta of one long Eurodollar futures | –$25 | –$25 | –$25 |
| Number of futures |
 |
 |
 |
| Aggregate delta for futures = NF × $25 | –$10,000 | –$9,500 | –$8,400 |
Note: Today is 15 April-01. Three payment dates remaining: 15 September-01, 15 March-02, 15 September-02. Total 
for the hedge = 400+380+340 = 1,120.
35.3.4 Hedging the Present Value of a Swaps Book
We can hedge the (present) value of the cash flows in the swap using any fixed income assets such as bonds, interest rate futures, and interest rate options – since their market value changes as interest rates change and therefore they can be used to offset any changes in the PV of the swaps position. By far the most popular method uses Eurodollar futures because they are liquid out to long maturities of 20–30 years.
When interest rates increase by 1 bp (per annum), the value of a receive-float, pay-fixed swap increases (i.e. positive delta), as the PV of the fixed payments is lower. To hedge we need to take a position in futures where a rise in interest rates leads to a loss on the futures – that is, today we take a long position in Eurodollar futures which have a ‘delta’ or ‘tick value’ of $25. Table 35.1 shows that the number of contracts needed (for each reset date) is:
Since we are only considering a potential change in interest rates over, say, 1 week, we can in principle use any interest rate futures contracts which mature after 1 week. But our rebalancing period might be longer than a week, in which case we might use longer dated Eurodollar contracts.
Consider implementing a strip hedge on 15 April-01. You take a long position in 400 September-01, 380 March-02 and 340 September-02 contracts – a total of 1,116 long contracts. Of course we could also use other Eurodollar strategies. For example, a stack hedge involves going long 1,116 September-01 contracts or 1,116 September-02 contracts.
If over the next few days (say) interest rates rise by 1 bp, then the (approximate) increase in the present value of the swaps position ($27,900) would be offset by the $27,900 losses on the long futures positions.4 So the mark-to-market value of the hedge position would remain constant over a ‘short’ time horizon.
We have removed the interest rate risk on the PV of the swaps book. The swap dealer will feel happy holding less of a (regulatory) ‘capital buffer’ against the market risk of its swaps book, since it is hedged and the risk of losses from changes in the value of the swaps book is minimal (and the regulator will agree). From time to time the swap dealer will rebalance its position in 1,116 futures and calculate a new hedge position for 
. This is because as interest rates change and as time moves on, this changes the delta of the swaps book.
35.3.5 Gamma and Convexity
Note that as swaps are equivalent to a ‘long-short’ bond portfolio, they have a non-linear (convex) response to interest rate changes. Our swaps ‘delta hedge’ is only effective for small changes in interest rates – or equivalently the hedge is only accurate over short time horizons. So the delta-hedged position should be rebalanced frequently (as we did when hedging options positions). If we thought there would be large changes in interest rates (over a short time period) then we require an estimate of the swaps' gamma. (This is a very similar concept to the convexity of a bond). As a Eurodollar futures contract has zero gamma we cannot use this to hedge the gamma of the swaps book.
To gamma hedge the swaps position, we require fixed income instruments that have a non-zero gamma – we could use FRAs, cash market bonds, options on T-bonds, or caps and floors. Using FRAs has the advantage that they have a zero vega and so do not introduce the additional complication of sensitivity to changes in the volatility (standard deviation) of interest rates. To see how this might work suppose the delta and gamma of our (total) swaps book are 
and 
respectively. We first gamma hedge and then delta hedge our swap position:
- Take positions in FRAs (and/or bonds) with a portfolio gamma
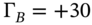, which then offsets the gamma of the swaps book. Suppose the FRAs used to obtain a zero gamma have a portfolio delta of 
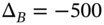. - The new delta for the ‘swaps plus FRAs’ is
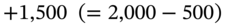. So if interest rates rise, the value of our current portfolio (i.e. swaps +FRAs) also rises. - Now take positions in Eurodollar futures to offset this ‘new delta’. We go long
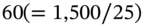Eurodollar futures. If interest rates rise there is a fall in value of our Eurodollar futures position and we close out at a loss, which balances the gain on our ‘swaps plus FRAs’.
The mark-to-market swaps position would then be largely protected from both large and small changes in interest rates. While swap dealers delta-hedge their swaps position with futures, they often do not gamma hedge and are therefore subject to some price risk on their swaps book, if there are large changes in interest rates over a short time period.
35.3.6 Allocation of Cash Flows to Standard Payment Dates
In the above example we assumed all cash flows from the swaps occurred at specific fixed dates, 6 months apart. This is unrealistic, as swap dealers will have net cash flows in their swaps book on almost every day of the year. We therefore have a problem in aggregating cash flows, as our swaps do not have cash flows on exactly the same payment dates. Swap cash flows that fall between ‘standard’ payment dates need to be allocated to ‘standard time buckets’ to make the above calculations manageable.
Suppose it is 15 February 
and the ‘standard’ payment dates we have chosen (arbitrarily) are at 
(15 June) and 
(15 December). A future known cash flow in the swap 
falls between these two standard payment dates (
) – for example on 10 October.
How should we allocate 
which accrues on 10 October, so that we end up with 
allocated to 
(15 June) and 
allocated to 
(15 December)? We use an allocation method that ensures the following:
- PV of the allocated cash flows
, 
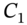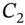equals the PV of the actual cash flow 
:
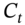where (continuously compounded) interest rates are measured from today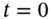 
(15 February, Figure 35.1). - The change in PV of the allocated cash flows
, 
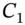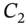equals the change in PV of the actual cash flow 
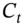(for a parallel shift in the yield curve):
where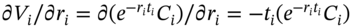 
, (for 
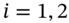) and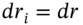 
for a parallel shift in the yield curve.5 Given current spot yields and the actual cash flow 
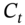, Equations (35.18) and (35.19) can be solved for the two unknowns, 
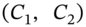– the dollar amounts to allocate to each standard ‘time-bucket’ at 
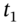and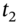 
. The coupons 
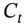include all cash flows in the swaps book which fall on 10 October. This allocation process has to be repeated for each cash flow that falls between any two standard payment dates.
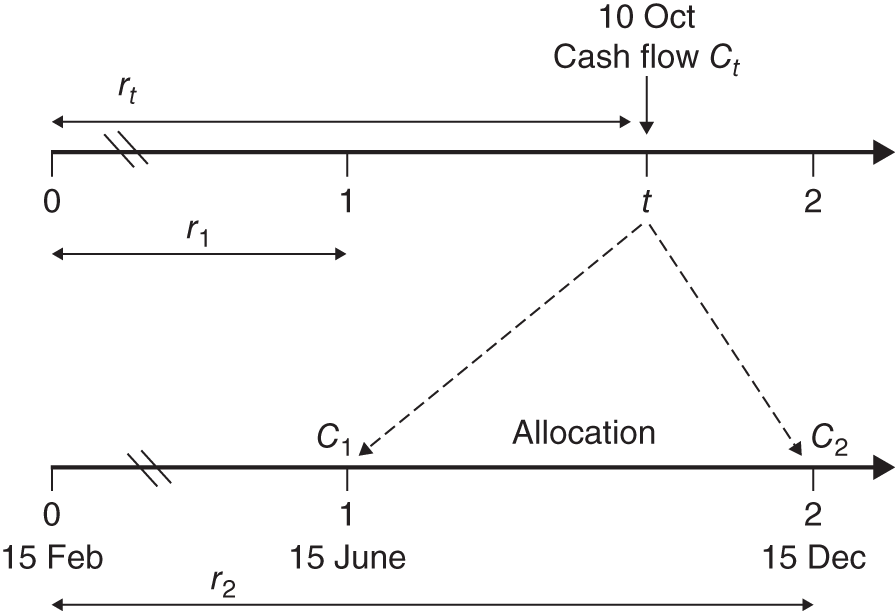
FIGURE 35.1 Allocation of cash flows
35.4 CREDIT RISK
Hedging credit risk in the swap's book is a key issue for a swap dealer. In a swap between a dealer-D and company-A only one party will face default risk at any one time. This is because at time 
if the value of the swap to the dealer is 
, then 
. It is only if 
and company-A defaults that there is a problem for the swap dealer. On the other hand if the swap dealer defaults when 
, then company-A is not harmed since the value of the swap to company-A is negative (
). In this case company-A could simply discontinue its swap payments, although in practice it may not do so because of general reputation effects in the market.
As the value of the swap changes over the life of the swap then either party can in principle be subject to default risk at some time during the life of the swap. However, because the principal in an interest rate swap is not actually exchanged, the default risk in an interest rate swap is less than the default risk of holding a portfolio of bonds – where the principal payments do influence the market value of the bond portfolio.
Credit risks in a fixed-for-floating swap are difficult to assess but these risks are often managed by using so-called credit enhancements. The most common method to limit credit risk is to pledge some sort of collateral, such as a line of credit from a bank or securities (e.g. T-bonds) which are held ‘in trust’ by a third party. For example, if one party undergoes a downgrade in its Standard and Poor's or Moody's credit rating, the collateral can be increased.
Alternatively, marking-to-market occurs when periodically the swap's value is calculated and the party with a negative swap value pays the counterparty this amount in cash. The swap rate then has to be reset to give a zero current value for the swap, based on current interest rates. The new swap rate determines the fixed payments in the swap until the next ‘mark-to-market’ date, when the procedure is repeated. Clearly this procedure is similar to margin payments in a futures contract.
Netting is a fairly simple form of credit enhancement. If at 
the swap dealer's position with company-Z is +$5m and on another swap contract with company-Z it is minus $4m then they can agree that the outstanding net position for the swap dealer is $1m. Hence if company-Z defaults, the swap dealer is only exposed to $1m credit risk rather than $5m.
However, it must be pointed out that in the event of bankruptcy by company-Z, it is not always clear that the bankruptcy courts will legally accept such a deal. It is worth noting that in the UK the House of Lords deemed that UK Local Authorities (i.e. equivalent to US Municipal Authorities), acted ultra vires (i.e. beyond the scope of authority) in entering into swap contracts and these contracts then became null and void – even though Local Authorities had the funds to pay the losses on their swaps positions. Total losses from vanilla interest rate swap defaults have historically been very low (e.g. less than ½% of the principal value of all swaps entered into). This is probably because swap deals tend to involve large well-capitalised organisations with high credit ratings and a ‘favourable reputation’ to preserve.
35.5 SUMMARY
- We can adapt the techniques used for plain vanilla fixed-for-floating interest rate swaps, to price and value more complex interest rate swaps.
- The swap rate is calculated assuming the swap must have zero value (to both parties) at inception – otherwise the swap would not take place. The swap rate is calculated by making the value of the fixed leg of the swap equal to the value of the floating leg, at inception of the swap.
- After the swap has been initiated the value of the swap may be positive or negative (to one of the parties).
- Complex interest rate swaps such as a spread-to-LIBOR swap, an off-market swap, a zero-coupon swap, a swap with a time varying swap rate (for the ‘fixed’ payments) and a swap with a variable notional principal, can all be priced by using a replication bond portfolio (i.e. a fixed rate bond and an FRN) to represent the cash flows in the swap.
- Hedging the market risk of swaps is usually done by calculating the delta of the swaps book (for standard time buckets) and using interest rate futures to delta hedge the interest rate risk. If the swap dealer is worried about large changes in interest rates then she can also hedge the gamma of her swaps book using FRAs, bonds, or (fixed income) options (although using options also introduces vega risk). After gamma hedging, the swaps dealer can then use interest rate futures to hedge the swap's delta.
- Credit risk of a swap can be mitigated using collateral, netting, and credit enhancements.
EXERCISES
Question 1
Suppose a plain vanilla interest rate ‘at-market’ swap (which has zero value at inception) has a swap rate of 
. You want a ‘receive-fixed, pay LIBOR’ swap at an ‘off-market’ fixed swap rate of 6.1%. What will happen when you enter the swap and what will determine your future fixed payments?
Question 2
Suppose a plain vanilla fixed-for-floating (LIBOR) ‘at-market’ swap (which has zero value at inception) has a swap rate of 6% p.a. You want a ‘spread-to-LIBOR’ swap where you receive LIBOR+2% and pay fixed. Will you pay more or less than 6% p.a. fixed? What alternative arrangement might happen when you enter the swap?
Question 3
A bank pays 30-day LIBOR-1% on its deposits and receives 360-day LIBOR from its bank loans. How might it use a yield curve swap to hedge its interest rate risk over the next 2 years?
Question 4
Why does it make sense for a swap dealer to hedge the market-to-market value of her (interest rate) swaps book rather than hedge just the future floating rate payments?
Question 5
What is the delta of a (interest rate) swaps book?
Question 6
You have delta-hedged your (interest rate) swaps book on Monday and are going to reassess the hedge in a week's time. On Monday, have you eliminated all market risk and if not how might you improve your hedged positon?
Question 7
When is a swap dealer subject to credit risk (due to a default of the swap counterparty)?
NOTES
- 1 We assume the T-bill is priced using simple yield (and not the T-bill discount rate).
- 2 A similar approach is used to determine ‘the Greeks’ in the BOPM.
- 3 Note that in practice not all the deltas will necessarily be positive, some of the deltas for the three net cash flows may be positive and some may be negative – depending on the aggregate net cash flows from all the swaps held by the swap dealer on these dates. Any negative cash flows reduce the overall swap's delta and of course the overall swap's delta may be negative.
- 4 Conversely, if interest rates fall, the value of the swaps position falls but the long futures can be closed out at a profit, so the hedge works in this case too.
- 5 For a single cash flow, the time to maturity equals the duration,
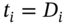. Hence, the change in the PVs can also be written in terms of the familiar duration relationships: 
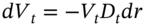for the actual cash flow and 
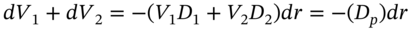where 
is defined as the portfolio duration of the two cash flows.