19.1 INTRODUCTION

The discrete Fourier transform (DFT) is a very important algorithm that finds use in many applications such as telecommunications, speech processing, image processing, medical imaging such as in computer assisted tomography (CAT), radar (synthetic aperture radar), sonar, and antenna array (phased arrays) [120, 121]. A very important application nowadays is the use of DFT techniques in orthogonal frequency division multiplexing (OFDM) as an efficient data modulation scheme. This technique is also extended for use in multiple-input multiple-output (MIMO) systems where each transmitter/receiver has multiple antennas to simultaneously transmit/receive multiple data streams in what is known as OFDM-MIMO systems [122]. This is not the forum to discuss what is OFDM and how it differs from the classic frequency division multiplexing (FDM). Excellent textbooks on digital communication cover such topics [113]

The DFT algorithm finds the spectrum of a periodic discrete-time signal with period N. The spectral component X(k) is obtained by the equation

(19.1)

where W_N is the twiddle factor, which equals the Nth root of unity and is given by

(19.2)

The dependence graph of the eight-point DFT algorithm is shown in Fig. 19.1. Input samples x(n) are represented by the vertical lines and output samples X(k) are represented by the horizontal lines. Input sample is represented by the point at location (n, k). The DFT algorithm is essentially a matrix–vector multiplication problem. For the case N = 8 we have

(19.3)

where

(19.4)

(19.5)

(19.6)

Figure 19.1 Dependence graph of an eight-point DFT algorithm.

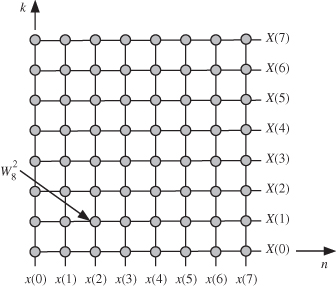
We removed the subscript from the twiddle factor to reduce clutter. We note that the powers of W are between 0 and 7.

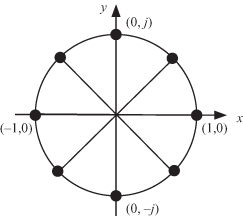
Figure 19.2 shows the values of the different powers of Wⁱ when 0 ≤ i < 8. We see that the twiddle factor powers are uniformly distributed around the unit circle. The angle between successive values is 2π/N = 45° for the case N = 8. Notice that the complex number Wⁱ has simple values when its angle is 0°, 90°, 180°, and 270°. Multiplying x(n) by these values in Eq. 19.1 becomes a trivial operation. Direct evaluation of Eq. 19.1 requires (N − 1)² complex number multiplications and N (N − 1) complex number additions. When N = 1,024, the number of operations becomes large. Very efficient techniques have been proposed for evaluating the DFT using much fewer operations than would be required by the original algorithm.

Figure 19.2 The values of twiddle powers Wⁱ when 0 ≤ i < 8.

Fast Fourier transform (FFT) was developed to reduce the number of operations required to obtain the DFT. The main concept in FFT is to break the original DFT sequence into two shorter sequences. The DFT of the shortened sequences are then recombined to give the DFT of the original sequence [123]. Assuming N is even, each of the N/2-point DFTs would require (N/2)² complex multiplications. A total of N²/2 complex multiplication would be required. Assuming N to be an integer power of two, the splitting process can be repeated until a series of simple two-point DFTs are required.