8.7 USEFUL THEOREMS
We show in this section some useful theorems related to the formal technique we proposed in the previous section. The following theorem discusses how we can check if a given algorithm is cycle free or not.
Theorem 8.1
An algorithm with W nodes/tasks is cycle free if and only if Ak has zeros in its main diagonal elements for 1 ≤ k ≤ W.
Proof:
Assume the algorithm is cycle free. In that case, we do not expect any diagonal element to be nonzero for Ak with k ≥ 1. The worst case situation is when our algorithm has all the nodes connected in one long string of W nodes as shown in Fig. 8.5a. The highest power for Ak is when k = W − 1 since this is the maximum length of the path between W nodes. AW = 0 since there is no path of length W. Thus, a cycle-free algorithm will produce zero diagonal elements for all powers of Ak with 1 ≤ k ≤ W.
Figure 8.5 Worst case algorithm that has 10 nodes. (a) When the algorithm is cycle free. (b) The longest possible cycle in an algorithm with 10 nodes is 10.
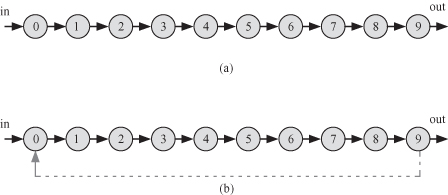
Now assume that all powers of Ak for 1 ≤ k ≤ W are all zero diagonal elements. This proves that we do not have any cycles of length 1 to W in the algorithm. This proves that the algorithm does not have any cycles since for W nodes, we cannot have a cycle of length greater than W. Figure 8.5b shows the longest possible cycle in an algorithm of W nodes/tasks.
The following theorem gives us the performance parameter D.
Theorem 8.2
A DAG has depth D if and only if the following two conditions are satisfied:
(8.11)
![]()
(8.12)
![]()
where 1 ≤ D ≤ W.
Proof:
Assume the DAG has depth D. This indicates that the maximum possible path length is D − 1. This implies the following two equations:
(8.13)
![]()
(8.14)
![]()
The condition AD = 0 above implies that there are no paths of length D or less in the algorithm and the longest path length is D − 1 according to Eq. 8.13. This is the length of the path that connects D nodes together. The first node is the input node and the last node is the output node.
Now assume the two conditions in (8.13) and (8.14) are true. Thus, the maximum path length is D for the algorithm.
The following theorem results as a consequence of the procedure for assigning execution order to the nodes according to Algorithm 8.1. It assures that the execution sequence assigned to each node is the smallest or earliest possible value.
Theorem 8.3
A node is assigned to sequence k if and only if it depends on one or more nodes assigned to sequence k − 1.
Proof:
Assume that node i is assigned sequence k. This implies that it must be executed after all the nodes in sequence k − 1. This implies that it depends on one or more nodes from that sequence. If that was not the case, the procedure of Algorithm 8.1 would have assigned a smaller sequence value to node i.
Now assume that node i depends on one or more nodes that belong to sequence K − 1. This node can only execute after all these nodes complete their execution. This implies that the sequence to be assigned to node i should have the value k.
The following theorem assures us that we can execute all nodes having the execution sequence in parallel or simultaneously.
Theorem 8.4
Nodes belong to the same sequence if and only if they are independent of each other and can be evaluated in parallel.
Proof:
Assume two nodes, i and j, have the same sequence Sk. This implies that the two nodes can be evaluated simultaneously in parallel and that they are independent of each other.
Now assume that two nodes, i and j, are independent and can be evaluated in parallel at the same time. This implies that the two nodes belong to the same sequence value. These two nodes could be moved to the earliest sequence, Sk, where both nodes depend on one or more nodes from sequence Sk−1.
The following theorem is unique to DAGs. It indicates that the last nodes executed are all output nodes and their outputs are not used to supply other nodes.
Theorem 8.5
A DAG has depth D if and only if all the nodes in sequence SD are output nodes.
Proof:
When the depth of the DAG is D, then nodes in sequence SD cannot be interior nodes. If a node were interior, then it must send its output data to a node i at sequence D + 1 since we do not have cycles. This would imply that node i will be evaluated at sequence SD+1 and the depth of the graph is at least D + 1. This contradicts the requirement that the depth is D.
Now assume that all nodes in sequence SD are output nodes. This implies that there are no more nodes that depend on them. Thus, the depth of the graph is D.
The following theorem is perhaps the most important theorem for DAGs. Essentially, it assures us that the sequence assigned to the nodes is the fastest possible schedule.
Theorem 8.6
The task execution schedule constructed from Algorithm 8.1 is the optimal schedule possible for the given DAG assuming we have enough computing resources to execute all the tasks in a given sequence level.
Theorems 8.3 and 8.5 indicate that we cannot reduce the depth of the graph by moving nodes from the given sequence to an earlier sequence. Hence, depth D cannot be reduced below its value.
Theorem 8.4 indicates that we have the maximum number of nodes in any given sequence level. So, we have the maximum number of nodes that could be assigned the same sequence order.
The above two paragraphs imply the following:
1. We have maximum parallelism at any sequence level.
2. We have the absolute minimum number of levels under the given assumptions.
Hence, the schedule obtained from Algorithm 8.1 is the optimal schedule.
The following theorem assures us that the execution order assigned to the nodes preserves the order dictated by the algorithm.
Theorem 8.7
The procedure in Algorithm 8.1 for setting the execution order of the algorithm tasks preserves the correctness of the algorithm.
Proof:
Two facts about the procedure assure us of the correctness of executing the algorithm:
1. The procedure in Algorithm 8.1 does not remove any parent from the parent set of any node and does not disturb the links between the tasks.
2. Theorem 8.3 assures us that any task will only be executed after all its parent tasks have been executed.
