Teofilo F. Gonzalez
University of California, Santa Barbara
25.3Binary Search Tree Implementations
25.4Balanced BST Implementation
Given an initially empty set S, the dictionary problem consists of executing online any sequence of operations of the form S.membership(s), S.insert(s), and S.delete(s), where each element s is an object (or point in one-dimensional space). Each object can be stored in a single word, and it takes O(1) time to store or retrieve it. It is well known that the set may be represented by using arrays (sorted or unsorted), linked lists (sorted or unsorted), hash tables, binary search trees, AVL-trees, B-trees, 2-3 trees, weighted balanced trees, or balanced binary search trees (i.e., 2-3-4 trees, symmetric B-trees, half balanced trees, or red-black trees).
The worst-case time complexity for performing each of these operations is O(log n), where n is the maximum number of elements in the set being represented, when using AVL-trees, B-trees (fixed order), 2-3 trees, weighted balanced trees, or balanced binary search trees. See Chapters 2, 3, 9, 11 and 16 for details on these structures. The insertion or deletion of elements in these structures requires a set of additional operations to preserve certain properties of the resulting trees. For binary search trees, these operations are called rotations, and for m-way search trees they are called splitting or combining nodes. The balanced binary search trees are the only trees that require a constant number of rotations for both the insert and delete operations [1,2].
This chapter discusses several algorithms [3,4] for the generalized dictionary problem for the case when the data is multidimensional, rather than one dimensional. Each data element consists of d-ordered components which we call ordered d-tuple or simply d-tuple. Each component contains a value which can be stored in a memory word and which can be compared against another value to determine whether the values are identical, the first value is larger than the second one, or the first value is smaller than the second one. The comparison operation between components takes constant time. We show that the basic multidimensional dictionary operations can be implemented to take O(d + log n), where n is the number of d-tuples in the set. We also show that other common operations can also be executed within the same time complexity bounds.
Let us now discuss one of the many applications of multidimensional dictionaries. Given a set of n points in multidimensional space and an integer D, the problem is to find the least number of orthogonal hypersquares (or d-boxes) of size D to cover all the points, that is, each of the points must be in at least one of the d-boxes. This covering problem arises in image processing, as well as when locating emergency facilities so that all users are within a reasonable distance of one of the facilities [5]. The problem has been shown to be NP-hard and several polynomial time approximation schemes for its solution have been developed [5]. The simplest approximation algorithm defines d-boxes along a multidimensional grid with grid d-boxes of length D. The approximation algorithm takes every d-dimensional point and by using simple arithmetic operations, including the floor function, finds its appropriate (grid) d-box. The d-box, which is characterized by d integer components, is inserted into a multidimensional dictionary and the operation is repeated for each d-dimensional point. Then one just visits all the d-tuples in the set and the d-boxes they represent is the solution generated by this simple approximation algorithm. Note that when a d-tuple is inserted into a multidimensional dictionary that already contains it, the dictionary will not change because dictionaries store sets, that is, multiple copies of the d-tuples are not allowed. Other applications of multidimensional dictionaries are when accessing multiattribute data by value. These applications include the management of geometrical objects and the solution of geometry search problems.
Given a d-tuple s in set S, one may access in constant time the ith element in the d-tuple by using the function s.x(i). In other words, the d-tuple s is simply (s.x(1), s.x(2),…, s.x(d)). In this chapter, we examine the methods given in References 3 and 4 to represent the data set and their algorithms to perform online any sequence of the multidimensional dictionary operations. The most efficient of the implementations performs each of the three dictionary operations in O(d + log n) time, where n is the number of d-tuples and d is the number of dimensions. Each of the insert and delete operations requires no more than a constant number of rotations. The best of the algorithms requires dn words to represent the d-tuples, plus O(n) additional space is required to keep additional pointers and data. Because we are using balanced binary search trees, we can also perform other operations efficiently. For example, find the (lexicographically) smallest or largest d-tuple (O(log n) time), print in lexicographic order (O(dn) time), and concatenation (O(d + log n) time). By modifying slightly the representation and introducing additional information, one can also find the (lexicographically) kth smallest or largest d-tuple efficiently (O(log n) time). In Section 25.5, we show that the structure given in Reference 4 may also be used to implement the split operation in O(d + log n) time and that the approach can also be used with other balanced structures, such as AVL-trees, weight-balanced trees, and so on.
It is interesting to note that three decades ago balanced structures were written off for this type of applications. As noted in Reference 6, “balanced tree schemes based on key comparisons (e.g., AVL-trees, B-trees, etc.) lose some of their usefulness in this more general context.” At that time the approach was to use tries in conjunction with balanced tree schemes to represent multidimensional data. We will elaborate on these structures after defining some terms.
Given a set of strings over an alphabet Σ, the tree of all their prefixes is called a trie (see Chapter 29). In Figure 25.1, we depict the trie for the set of strings over the English alphabet T = {akam, aklm, cmgi, cmos, cors, corv, nort, novl, novn}. In this case, all the elements in the trie have the same number of symbols, but in general a trie may contain string with different number of symbols. Each node x in a trie is the destination of all the strings with the same prefix (say px) and node x consists of a set of element–pointer pairs. The first component of the pair is an alphabet element and the second one is a pointer to a subtrie that contains all the strings with prefix px followed by the alphabet element. In Figure 25.1, the pairs for a trie node are represented by the edges emanating from the lower portion of the circle that represents a node. Note that no two element-pointer pairs for a trie node have the same first component or the same second component. The set of element–pointer pairs in a trie node may be represented in different ways. For example, one may store the element–pointer pairs for each internal node as follows:
1.An array of m pointers, where m is the number of elements in the alphabet Σ. In this case, one needs to define a function to translate each element in the alphabet to an integer in the range [0, m − 1]. The function can normally be implemented to take constant time;
2.A sorted linked list with all the symbols and corresponding pointers of the branches emanating from the node [7];
3.A binary search tree with all the symbols and corresponding pointers of the branches emanating from the node [8].
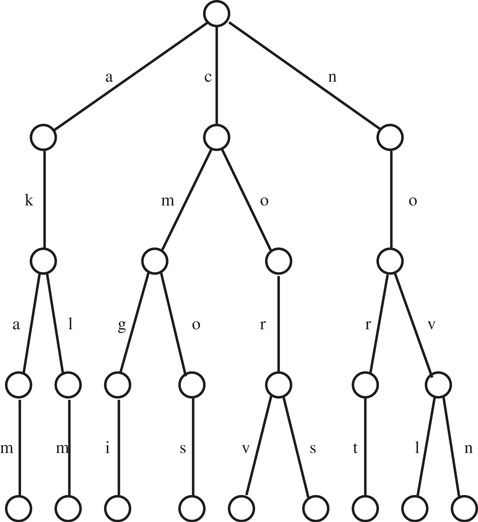
Figure 25.1Trie for set T.
We shall refer to the resulting structures as trie-array, trie-list, and trie-bst, respectively. These are by no means all the possibilities. For example, later on we discuss hybrid representations that have some interesting properties.
For multidimensional dictionaries defined over the set of integers [0, m), the trie method treats a point in d-space as a string with d elements defined over the alphabet Σ = {0, 1, …, m − 1} (see Figure 25.1). For the trie-array representation, the element–pointer pairs in a trie node are represented by an m-element sequential array of pointers. The ith pointer corresponds to the ith alphabet symbol, and a null pointer is used when the corresponding alphabet element is not part of any element–pointer pair. The space required to represent n d-tuples in this structure is at most dnm pointers, but the total amount of information can be represented using dn log m bits. The insert and delete operations take O(md) time, because either of these operations may add or delete d − 1 trie nodes and each node includes an m-component array of pointers. On the other hand, the membership operation takes only O(d) time. This is the fastest way of implementing the membership operation no matter what structure is used to represent the set. The trie-array implementation is not possible when m is large because there will be too much space wasted. The trie-list representation mentioned above is much better for this scenario. In this case, the list of element–pointer pairs is stored in a sorted linked list. The list is sorted with respect to the alphabet elements, that is, the first component in the element–pointer pairs. In the trie-bst representation, the element–pointers are stored in a binary search tree. The ordering is with respect to the alphabet elements. In the former case, we use dn memory locations for the d-tuples, plus 2dn pointers, and in the latter case one needs 3dn pointers. The time complexity for insert, delete, and membership in both of these representations is O(d + n). It is important to note that there are two types of pointers: the trie pointers and the linked list or binary search tree pointers.
In practice, one may use hybrid structures in which some nodes in the trie are trie-arrays and others are trie-lists, and depending on the number of element–pointer pairs one transforms from one representation to the other. For example, if the number of element–pointer pairs becomes more than some bound bu one uses trie-array nodes, but if it is less than bl then one uses the trie-list nodes. If it is some number between these two bounds, then either representation is fine to use. By using appropriate values for bl and bu in this approach, we can avoid “trashing” which means that the algorithm spends most of the time changing back and forth from one representation to the other.
Bentley and Saxe [9] used a modified version of the trie-bst implementation. In this case, the binary search tree is replaced by a completely balanced binary tree. That is, each binary search tree or subtree for trie node x with k element–pointer pairs has as root an element–pointer pair (y, ptr) such that the median of the ordered strings (with prefix equal to the prefix of the trie node x (denoted by px) plus any of the k alphabet elements in the k element–pointer pairs) has as prefix px followed by y. For example, the root of the trie in Figure 25.1 has the pair with alphabet element c, and the root of the subtrie for the prefix no is the pair with alphabet element v. This balanced structure is the best possible when the trie does not change or it changes very slowly like in multikey sorting or restricted searching [10,11]. Since the overall structure is rigid, it can be shown that rebalancing after inserting or deleting an element can be very expensive and therefore not appropriate in a dynamic environment.
Research into using different balanced strategies for the trie-bst structures has lead into structures that use fixed order B-trees [12], weight-balanced trees [6], AVL-trees [13], and balanced binary search trees [14]. It has been shown that insert, delete, and membership for multidimensional dictionaries for all of the above structures take O(d + log n) time in the worst case, except for weight-balanced trees in which case it is an expected time complexity bound. The above procedures are complex and require balancing criteria in addition to the obvious ones. Also, the number of rotations needed for these insert and delete operations is not bounded by a constant. Vaishnavi [14] used balanced binary search trees that require only a constant number of rotations, however, since one may encounter d trees, the total number of rotations are no longer bounded by a constant. He left it as an open problem to design a structure such that multidimensional dictionaries can be implemented so that only a constant number of rotations are performed after each insert and delete operation.
25.3Binary Search Tree Implementations
As pointed out by Gonzalez [3,4], using a balanced binary search tree (without a trie) and storing each tuple at each node lead to membership (and also insert and delete) algorithms that take O(d log n) time, where n is the number of elements in the tree, because one needs to compare the element being searched with the d-tuples at each node. One can go further and claim that for some problem instances it actually requires Θ(d log n) time. Gonzalez [4] also points out that simple shortcuts to the search process do not work. For example, if we reach a node in the search such that the first k components are identical, one may be tempted to conclude that in the subtree rooted at that node one needs to search only from position k + 1 to d in the d-tuples. This is false because the k-component prefixes of all the d-tuples in a subtree may vary considerable in a binary search tree. One can easily show that even the membership operation cannot be implemented this way. However, this variation is more predictable when comparing against the smallest or largest d-tuple in a subtree. This is a key idea exploited in Reference 3.
Manber and Myers [15] developed an efficient algorithm that given an N symbol text it finds all the occurrences of any input word q. The scenario is that the text is static, but there will be many word searches. Their approach is to preprocess the text and generate a structure where the searching can be performed efficiently. In their preprocessing stage, they construct a sorted list with all the N suffixes of the text. Locating all the occurrences of a string q reduces to performing two binary search operations in the list of suffixes, the first for the first suffix that contains as prefix q and the second search is for the last suffix that contains as prefix q. Both searches are similar, so let’s discuss the first one. This operation is similar to the membership operation discussed in this chapter. Manber and Myers [15] binary search process begins by letting L (R) be the largest (smallest) string in the list. Then l (r), the index of the first element where L (R) differs from q, is computed. Note that if two strings are identical the index of the first component where they differ is set to the length of string plus 1. We use this convention throughout this chapter. The middle entry M in the list is located and then they compute the index of the first component where M and q differ. If this value is computed the obvious way, then the procedure will not be efficient. To do this efficiently they compute it with l, r as well as the index of the first component where M and L, and M and R differ. These last two values are precomputed in the preprocessing stage. This indirect computation may take O(|q|) time; however, overall the phases of the computation the process takes at most O(|q|) time. The advantage of this approach is that it requires only O(N) space, and the preprocessing can be done in O(N) expected time [15]. The disadvantage is that it is not dynamic. Updating the text requires expensive recomputation of the precomputed data, that is, one needs to find the first component where many pairs in the list differ in order to carry out efficiently the binary search process. For their application [15], the text is static. The time required to do the search for q is O(|q| + log N) time. This approach results in a structure that is similar to the fully balanced tree strategy in Reference 9.
Gonzalez [3] solved Vaishnavi’s open problem by designing a binary tree data structure where the multidimensional dictionary operations can be performed in O(d + log n) time while performing only a constant number of rotations. To achieve this goal the set of d-tuples S is represented in a balanced binary search tree that contains additional information at each node. This additional information is similar to the one in the lists of Manber and Myers [15], but it can be recomputed efficiently as we insert and delete elements. The disadvantage is that the membership operation is more complex. But all the procedures developed in Reference 3 are simpler than the ones given in References 6,12–14. One just needs to add a few instructions in addition to the normal code required to manipulate balanced binary search trees [2]. The additional information in Reference 3 includes for every node v in the tree the index of the first element where v and the smallest (largest) d-tuple in the subtree rooted at v differ as well as a pointer to this d-tuple. As mentioned above, testing for membership is more complex. At each iteration in the search process [3], we are at the tree node t and we know that if q is in the tree then it is in the subtree rooted at t. The algorithm knows either the index of a component where q and the smallest d-tuple in the subtree t differ, or the index of a component where q and the largest d-tuple in the subtree t differ. Then the algorithm determines that q is in node t or it advances to the left or right subtrees of node t. In either case, it maintains the above invariant. It is important to point out that the invariant is: “the index of a component where q and the smallest d-tuple in the subtree differ” rather than the “the first index of a …” It does not seem possible to find “the first index …” in this structure efficiently with the information stored in the tree. This is not a big problem when q is in the tree since it will be found quickly, but if it is not in the tree then in order to avoid reporting that it is in the tree one must perform an additional verification step at the end that takes O(d) time. Gonzalez [3] calls this search strategy “assume, verify, and conquer” (AVC). That is, in order to avoid multiple expensive verification steps one assumes that some prefixes of strings match. The outcome of the search depends on whether or not these assumptions were valid. This can be determined by performing one simple verification step that takes O(d) time. The elimination of multiple verification steps is very important because in the worst case there are Ω(log n) of such steps, and each one could take Ω(d) time. The difference between this approach and the one in Reference 15 is that Manber and Myers compute the first element where M and q differ, whereas Gonzalez [3] computes an element where M and q differ. As we said before, in Gonzalez [3] structure one cannot compute efficiently the first element where M and q differ, whereas in Reference 15 this is possible because it is a static structure.
Gonzalez [4] modified the structure in Reference 3 to one that follows the search process in Reference 15. The new structure, which we discuss in Section 25.4, is in general faster to update because for every node t one keeps the index of the first component where the d-tuple stored at node t and the smallest (largest) d-tuple greater (smaller) than all the d-tuples in the subtree rooted at t (if any) differ, rather than the one between node t and the smallest (largest) d-tuple in its subtree rooted at t as in Reference 3. In this structure, only several nodes have to be modified when inserting a node or deleting a leaf node, but in the structure in Reference 3 one may need to update O(log n) nodes. Deleting a nonleaf node from the tree requires more work in this structure than in Reference 3, but membership testing is simpler in the structure in Reference 4. To summarize, the membership algorithm in Reference 4 mimics the search procedure in Reference 15, but follows the update approach developed in Reference 3. Gonzalez [4] established that the dictionary operations can be implemented to take O(d + log n) time while performing only a constant number of rotations for both insert and delete. Other operations which can be performed efficiently in this multidimensional balanced binary search trees are: finding the (lexicographically) smallest (largest) d-tuple (O(log n) time), print in lexicographic order (O(dn) time), and concatenation (O(d + log n) time). Finding the (lexicographically) kth smallest (largest) d-tuple can also be implemented efficiently (O(log n) time) by adding to each node the number of nodes in its left subtree. The asymptotic time complexity bound for the procedures in Reference 4 is identical to the ones in Reference 3, but the procedures in Reference 4 are simpler. To distinguish this new type of balanced binary search trees from the classic ones and the ones in Reference 3, we refer to these trees as multidimensional balanced binary search trees. In this article, we follow the notation in Reference 4.
In Section 25.5, we show that the rotation operation in Reference 4 can be implemented to take only constant time by making some rather simple operations that were first discussed in Reference 16. The implication of this, as pointed out in Reference 16, is that the split operation can also be implemented to take O(d + log n). Also, the efficient implementation of the rotation operation allows us to use the technique in Reference 4 on many other balanced structures, such as AVL, weight balanced, and so on, since performing O(log n) rotations does not limit the applicability of the techniques in Reference 4. These observations were first reported in Reference 16, where they present a similar approach, but in a more general setting.
25.4Balanced BST Implementation
Let us now discuss the data structure and algorithms for the multidimensional dictionaries given in Reference 4. The representation is based on balanced binary search trees, without external nodes, that is, each node represents one d-tuple. Balanced binary search trees and their algorithms [2] are like the typical “bottom-up” algorithms for the Red-Black trees. The ordering of the d-tuples is lexicographic. Each node t in the tree rooted at r has the following information in addition to the color bit required to manipulate balanced binary search trees [2]. Note that if two d-tuples are identical the index of the first component where they differ is set to d + 1. We use this convention throughout this chapter.
|
s: |
The d-tuple represented by the node. The individual components may be accessed as s.x(1), s.x(2), …, s.x(d) |
|
lchild: |
Pointer to the left subtree of t |
|
rchild: |
Pointer to the right subtree of t |
|
lptr: |
Pointer to the node with largest d-tuple in r with value smaller than all the d-tuples in the subtree rooted at t, or null if no such d-tuple exists |
|
hptr: |
Pointer to the node with smallest d-tuple in r with value larger than all the d-tuples in the subtree rooted at t, or null if no such d-tuple exists |
|
lj: |
Index of first component where s and the d-tuple at the node pointed at by lptr differ, or one if lptr = null |
|
hj: |
Index of first component where s and the d-tuple at the node pointed at by lptr differ, or one if hptr = null |
The insert, delete, and membership procedures perform the operations required to manipulate balanced binary search trees, and some new operations to update the structure. The basic operations to manipulate balanced binary search trees are well known [1,2]; so we only discuss in detail the new operations.
To show that membership, insert, and delete can be implemented to take O(d + log n) time, we only need to show that the following (new) operations can be performed O(d + log n) time.
A. Given the d-tuple q determine whether or not it is stored in the tree
B. Update the structure after adding a node (just before rotation(s), if any)
C. Update the structure after performing a rotation
D. Update the structure after deleting a leaf node (just before rotation(s), if any)
E. Transform the deletion problem to deletion of a leaf node.
The membership operation that tests whether or not the d-tuple q given by (q.x(1), q.x(2), …, q.x(d)) is in the multidimensional binary search tree (or subtree) rooted at r appears in [4] and implements (A). The basic steps are as follows. Let t be any node encountered in the search process in the multidimensional balanced binary search tree rooted at r. Let prev(t) to be the d-tuple in r with largest value but whose value is smaller than all the d-tuples stored in the subtree rooted at t, unless no such tuple exists in which case its value is ( − ∞, − ∞, …, − ∞), and let next(t) be the d-tuple in r with smallest value but whose value is larger than all the d-tuples stored in the subtree rooted by t, unless no such tuple exists in which case its value is ( + ∞, + ∞, …, + ∞). The following invariant is maintained throughout the search process. During the search we will be visiting node t which is initially the root of the tree. The value of dlow is the index of the first component where q and prev(t) differ, and variable dhigh is the index of the first component where q and next(t) differ. The d-tuple being search for, q, has value (lexicographically) greater than prev(t) and (lexicographically) smaller than next(t).
The computation of j, the index of the first component where t.s and q differ is performed as follows: when dlow ≥ dhigh, then either (1) dlow = t.lj in which case j is just min {dlow, t.lj}, or (2) dlow = t.lj in which case j is set to the index of the first component starting at position dlow where q and t.s differ. The case when dlow < dhigh is similar and appears in Reference 4. Gonzalez [4] proved that by setting j by the above procedure will set it to the index of the first component where t.s and q differ. When j is equal to d + 1, then q is the d-tuple stored in t and the procedure returns the value of true. Otherwise by comparing the jth element of q and t, the procedure decides whether to search in the left or right subtrees of t. In either case dhigh or dlow is set appropriately and the invariant holds at the next iteration. The time complexity at each level is not bounded by a constant; however, it is bounded by 1 plus the difference between the new and old values of max{dlow, dhigh}. Since max{dlow, dhigh} does not decrease and it is at most d + 1 at the end of each operation, it follows that the total number of operations performed is of order d plus the height of the tree (O(log n)). Correctness and efficiency are established in the following lemma whose proof appears in Reference 4.
Lemma 25.1
Given a d-tuple q, the formal procedure membership (q, r) given in Reference 4 determines whether or not q is in the multidimensional balanced binary search tree rooted at r in O(d + log n) time [4].
For operation (B), a node is added as a leaf node, the information that needs to be set for that node are the pointers lptr and hptr which can be copied from the parent node, unless there is no parent in which case they are set to null. The values lj and hj can be computed directly in O(d) time. A predecessor of the node added also needs its lptr and lj, or hptr and hj values changed. This can be easily done in O(d), by remembering the node in question during the search process, that is, the last node where one makes a left turn (moving to the leftchild) or the last one where one makes a right turn (moving to the rightchild).
Lemma 25.2
After inserting a node q in a multidimensional balanced binary search tree and just before rotation, the structure can be updated as mentioned above in O(d + log n) time [4].
The implementation of operation (D) is similar to the one for (B), therefore, it will not be discussed further. The rotation operation (C) can be reduced to a simple rotation, as a double or triple rotation can reduced to two and three simple rotations, respectively. A simple rotation is shown in Figure 25.2. It is simpler to implement the rotation operation by moving the nodes rather than just their values, because this reduces the number of updates that need to be performed. Clearly, the only nodes whose information needs to be updated are b, d and the parent of d. This can be implemented to take O(d) time.
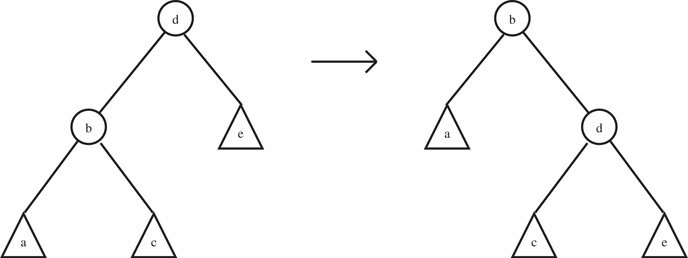
Figure 25.2Rotation.
Lemma 25.3
After a rotation in a multidimensional balanced binary search tree, the structure can be updated as mentioned above in O(d) time [4].
Operation (E) is more complex to implement. It is well known [17] that the problem of deleting an arbitrary node from a balanced binary search tree can be reduced to deleting a leaf node by applying a simple transformation. Since all cases are similar, let’s just discuss the case shown in Figure 25.3. The node to delete is a which is not a leaf node. In this case, node b contents are moved to node a, and now we delete the old node b which is labeled x. As pointed out in Reference 4, updating the resulting structure takes O(d + log n) time. Since the node labeled x will be deleted, we do not need to update it. For the new root (the one labeled b), we need to update the lj and hj values. Since we can use directly the old lptr and hptr pointers, the update can be done in O(d) time. The lj (hj) value of the nodes (if any) in the path that starts at the right (left) child of the new root that continues through the leftchild (rightchild) pointers until the null pointer is reached needs to be updated. There are at most O(log n) of such nodes. However, the d-tuples stored at each of these nodes are decreasing (increasing) in lexicographic order when traversing the path top down. Therefore, the lj (hj) values appear in increasing (decreasing) order. The correct values can be easily computed in O(d + log n) time by reusing previously computed lj (hj) values while traversing the path top down. The following lemma, whose proof is omitted, summarizes these observations. Then we state the main result in Reference 4 which is based on the above discussions and the lemmas.
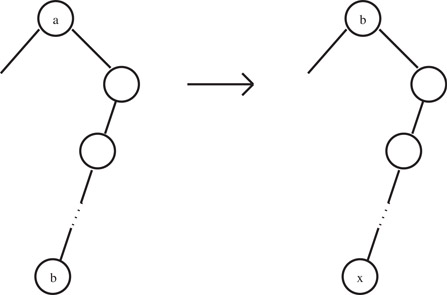
Figure 25.3Transforming deletion of an arbitrary node to deletion of a leaf node.
Lemma 25.4
Transforming the deletion problem to deleting a leaf node can be performed, as mentioned above, in O(d + log n) time [4].
Theorem 25.1
Any online sequence of operations of the form insert, delete, and membership, for any d-tuple can be carried out on a multidimensional balanced binary search tree in O(d + log n) time, where n is the current number of points, and each insert and delete operation requires no more than a constant number of rotations [4].
With respect to other operations, one can easily find the smallest or largest d-tuple in O(log n) time by just taking all the leftchild or rightchild pointers. By traversing the tree in inorder one can print all the d-tuples in increasing in O(dn) time. An O(d + log n) time algorithm to concatenate two sets represented by the structure can be easily obtained by using standard procedures provided that all the d-tuples in one set are in lexicographic order smaller than the ones in the other set. The kth smallest or largest d-tuple can be found in O(log n) time after adding to each node in the tree the number of nodes in its left subtree.
The split operation is given a d-tuple q and a set represented by a multidimensional balanced binary search tree t, split t into two multidimensional balanced binary search trees: one containing all the d-tuples in lexicographic order smaller than or equal to q and the other one containing the remaining elements. At first glance, it seems that the split operation cannot be implemented within the O(d + log n) time complexity bound. The main reason is that there could be Ω(log n) rotations and each rotation takes time proportional to d. However, the analysis in Reference 4 for the rotation operation which is shown in Section 25.4 can be improved and one can show that it can be easily implemented to take constant time. The reason for this is that for a simple rotation, see Figure 25.2, the lj or hj value needs to be updated for the node labeled b, and we know the lptr and hptr pointers. This value can be computed from previous values before the rotation, that is, the lj and hj values for node b and the fact that the rptr value for b is node d before the rotation. The other value to be updated is the lj value for node d after the rotation, but this is simply the rj value for node d before the rotation.
The efficient implementation of the rotation operation allows us to use the same technique on many other balanced structures, such as AVL-trees, weight-balanced trees, and so on, since having O(log n) rotations does not limit its applicability.
On average, the trie-bst approach requires less space to represent the d-tuples than our structures. However, multidimensional balanced binary search trees have simple procedures that take only O(d + log n) time, and only a constant number of rotations are required after each insert and delete operations. Furthermore, operations like finding the (lexicographically) smallest or largest d-tuple (O(log n) time), print in lexicographic order (O(dn) time), concatenation (O(d + log n) time), and split (O(d + log n) time) can also be performed efficiently in this new structure. This approach can also be used in other balanced structures, such as AVL-trees, weight-balanced trees, and so on.
1.H. J. Olivie, A New Class of Balanced Search Trees: Half-Balanced Binary Search Trees, PhD thesis, University of Antwerp, U.I.A., Wilrijk, Belgium, 1980.
2.R. E. Tarjan, Updating a balanced search tree in O(1) rotations, Information Processing Letters, Vol. 16, 1983, pp. 253–257.
3.T. Gonzalez, The on-line D-dimensional dictionary problem, Proceedings of the Third Symposium on Discrete Algorithms, Orlando, Florida, January 1992, pp. 376–385.
4.T. Gonzalez, Simple algorithms for the on-line multidimensional problem and related problems, Algorithmica, Vol. 28, 2000, pp. 255–267.
5.T. Gonzalez, Covering a set of points with fixed size hypersquares and related problems, Information Processing Letters, Vol. 40, 1991, pp. 181–188.
6.K. Mehlhorn, Dynamic binary search, SIAM Journal of Computing, Vol. 8, 1979, pp. 175–198.
7.E. H. Sussenguth, Use of tree structures for processing files, Communications of the ACM, Vol. 6, 1963, pp. 272–279.
8.H. A. Clampett, Randomized binary searching with the tree structures, Communications of the ACM, Vol. 7, 1964, pp. 163–165.
9.J. L. Bentley, and J. B. Saxe, Algorithms on vector sets, SIGACT News, Fall 1979, pp. 36–39.
10.D. S. Hirschberg, On the complexity of searching a set of vectors, SIAM Journal on Computing, Vol. 9, 1980, pp. 126–129.
11.S. R. Kosaraju, On a Multidimensional Search Problem, 1979 ACM Symposium on the Theory of Computing, Atlanta, Georgia, pp. 7–73.
12.R. H. Gueting, and H. P. Kriegel, Multidimensional B-tree: An efficient dynamic file structure for exact match queries, Proceedings 10th GI Annual Conference, Informatik Fachberichte, Springer-Verlag, Berlin-Heidelberg-New York, 1980, pp. 375–388.
13.V. Vaishnavi, Multidimensional height-balanced trees, IEEE Transactions on Computers, Vol. c-33, 1984, pp. 334–343.
14.V. Vaishnavi, Multidimensional balanced binary trees, IEEE Transactions on Computers, Vol. 38, 1989, pp. 968–985.
15.U. Manber, and G. Myers, Suffix arrays: A new method for on-line string searches, SIAM Journal of Computing, Vol. 22, 1993, pp. 935–948.
16.R. Grossi, and G. F. Italiano, International colloquium on automata, languages and programming (ICALP 99), Lecture Notes in Computer Science, Springer-Verlag, Berlin-Heidelberg-New York, Vol. 1644, 1999, pp. 372–381.
17.L. J. Guibas, and R. Sedgewick, A dichromatic framework for balanced trees, Proceedings of the 19th Annual IEEE Symposium on Foundations of Computer Science, University of Michigan, Ann Arbor, 1978, pp. 8–21.
