Leonidas Guibas
Stanford University
24.2Motion in Computational Geometry
Convex Hull Example•Performance Measures for KDS•The Convex Hull, Revisited
Extent Problems•Proximity Problems•Triangulations and Tilings•Collision Detection•Connectivity and Clustering•Visibility•Result Summary•Open Problems
24.7Sources and Related Materials
Motion is ubiquitous in the physical world, yet its study is much less developed than that of another common physical modality, namely shape. While we have several standardized mathematical shape descriptions, and even entire disciplines devoted to that area—such as Computer-Aided Geometric Design (CAGD)—the state of formal motion descriptions is still in flux. This in part because motion descriptions span many levels of detail; they also tend to be intimately coupled to an underlying physical process generating the motion (dynamics). Thus, until recently, proper abstractions were lacking and there was only limited work on algorithmic descriptions of motion and their associated complexity measures. This chapter aims to show how an algorithmic study of motion is intimately tied via appropriate data structures to more classical theoretical disciplines, such as discrete and computational geometry. After a quick survey of earlier work (Sections 24.2 and 24.3), we devote the bulk of this chapter to discussing the framework of Kinetic Data Structures (Section 24.4) [1,2] and its many applications (Section 24.5). We also briefly discuss methods for querying moving objects (Section 24.6).
24.2Motion in Computational Geometry
Motion has not been studied extensively within the context of theoretical computer science. Until recently, there were only sporadic investigations of moving objects in the computational geometry literature. Dynamic computational geometry refers to the study of combinatorial changes in a geometric structure, as its defining objects undergo prescribed motions. For example, we may have n points moving linearly with constant velocities in , and may want to know the time intervals during which a particular point appears on their convex hull, the steady-state form of the hull (after all changes have occurred), or get an upper bound on how many times the convex hull changes during this motion. Such problems were introduced and studied in Reference 3.
A number of other authors have dealt with geometric problems arising from motion, such as collision detection or minimum separation determination [4–6]. See also Chapter 57. For instance, [6] shows how to check in subquadratic time whether two collections of simple geometric objects (spheres, triangles) collide with each other under specified polynomial motions.
An issue with the above research is that object motion(s) are assumed to be known in advance, sometimes in explicit form (e.g., points moving as polynomial functions of time). Indeed, the proposed methods reduce questions about moving objects to other questions about derived static objects.
While most evolving physical systems follow known physical laws, it is also frequently the case that discrete events occur (such as collisions) that alter the motion law of one or more of the objects. Thus motion may be predictable in the short term, but becomes less so further into the future. Because of such discrete events, algorithms for modeling motion must be able to adapt in a dynamic way to motion model modifications. Furthermore, the occurrence of these events must be either predicted or detected, incurring further computational costs. Nevertheless, any truly useful model of motion must accommodate this on-line aspect of the temporal dimension, differentiating it from spatial dimensions, where all information is typically given at once.
In real-world settings, the motion of objects may be imperfectly known and better information may only be obtainable at considerable expense. The model of data in motion of [7] assumes that upper bounds on the rates of change are known, and focuses on being selective in using sensing to obtain additional information about the objects, in order to answer a series of queries.
Suppose we are interested in tracking high-level attributes of a geometric system of objects in motion such as, for example, the convex hull of a set on n points moving in . Note that as the points move continuously, their convex hull will be a continuously evolving convex polygon. At certain discrete moments, however, the combinatorial structure of the convex hull will change (i.e., the circular sequence of a subset of the points that appear on the hull will change). In between such moments, tracking the hull is straightforward: its geometry is determined by the positions of the sequence of points forming the hull. How can we know when the combinatorial structure of the hull changes? The idea is that we can focus on certain elementary geometric relations among the n points, a set of cached assertions, which altogether certify the correctness of the current combinatorial structure of the hull. If we have short-term information about the motion of the points, then we can predict failures of these assertions in the near future. Furthermore, we can hope to choose these certifying relations in such a way so that when one of them fails because of point motion, both the hull and its set of certifying relations can be updated locally and incrementally, so that the whole process can continue.
•Kinetic data structure: A kinetic data structure (KDS) for a geometric attribute is a collection of simple geometric relations that certifies the combinatorial structure of the attribute, as well as a set of rules for repairing the attribute and its certifying relations when one relation fails.
•Certificate: A certificate is one of the elementary geometric relations used in a KDS.
•Motion plan: An explicit description of the motion of an object in the near future.
•Event: An event is the failure of a KDS certificate during motion. If motion plans are available for all objects in a certificate, then the future time of failure for this certificate can be predicted. Events are classified as external when the combinatorial structure of the attribute changes, and internal, when the structure of the attribute remains the same, but its certification needs to change.
•Event queue: In a KDS, all certificates are placed in an event queue, according to their earliest failure time.
The inner loop of a KDS consists of repeated certificate failures and certification repairs, as depicted in Figure 24.1.
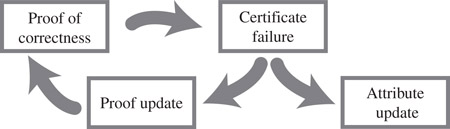
Figure 24.1The inner loop of a kinetic data structure.
We remark that in the KDS framework, objects are allowed to change their motions at will, with appropriate notification to the data structure. When this happens all certificates involving the object whose motion has changed must re-evaluate their failure times.
Suppose we have four points a, b, c, and d in , and wish to track their convex hull. For the convex hull problem, the most important geometric relation is the CCW predicate: CCW(a, b, c) asserts that the triangle abc is oriented counterclockwise. Figure 24.2 shows a configuration of four points and four CCW relations that hold among them. It turns out that these four relations are sufficient to prove that the convex hull of the four points is the triangle abc. Indeed the points can move and form different configurations, but as long as the four certificates shown remain valid, the convex hull must be abc.
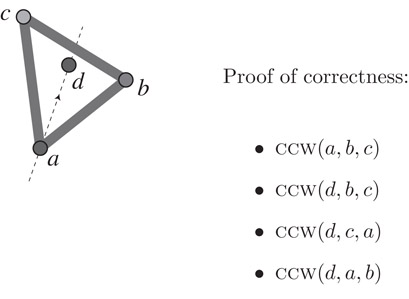
Figure 24.2Determining the convex hull of the points.
Now suppose that points a, b, and c are stationary and only point d is moving with a known plan, as shown in Figure 24.3. At some time t1 the certificate CCW(d, b, c) will fail, and at a later time t2 CCW(d, a, b) will also fail. Note that the certificate CCW(d, c, a) will never fail in the configuration shown even though d is moving. So the certificates CCW(d, b, c) and CCW(d, a, b) schedule events that go into the event queue. At time t1, CCW(d, b, c) ceases to be true and its negation, CCW(c, b, d), becomes true. In this simple case the three old certificates, plus the new certificate CCW(c, b, d) allow us to conclude that convex hull has now changed to abdc.
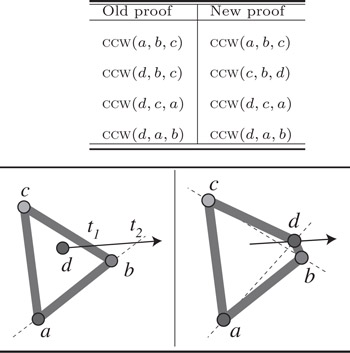
Figure 24.3Updating the convex hull of the points.
If the certificate set is chosen wisely, the KDS repair can be a local, incremental process—a small number of certificates may leave the cache, a small number may be added, and the new attribute certification will be closely related to the old one. A good KDS exploits the continuity or coherence of motion and change in the world to maintain certifications that themselves change only incrementally and locally as assertions in the cache fail.
24.4.2Performance Measures for KDS
Because a KDS is not intended to facilitate a terminating computation but rather an on-going process, we need to use somewhat different measures to assess its complexity. In classical data structures there is usually a tradeoff between operations that interrogate a set of data and operations that update the data. We commonly seek a compromise by building indices that make queries fast, but such that updates to the set of indexed data are not that costly as well. Similarly in the KDS setting, we must at the same time have access to information that facilitates or trivializes the computation of the attribute of interest, yet we want information that is relatively stable and not so costly to maintain. Thus, in the same way that classical data structures need to balance the efficiency of access to the data with the ease of its update, kinetic data structures must tread a delicate path between “knowing too little” and “knowing too much” about the world. A good KDS will select a certificate set that is at once economical and stable, but also allows a quick repair of itself and the attribute computation when one of its certificates fails.
•Responsiveness: A KDS is responsive if the cost, when a certificate fails, of repairing the certificate set and updating the attribute computation is small. By “small” we mean polylogarithmic in the problem size—in general we consider small quantities that are polylogarithmic or O(nε) in the problem size.
•Efficiency: A KDS is efficient if the number of certificate failures (total number of events) it needs to process is comparable to the number of required changes in the combinatorial attribute description (external events), over some class of allowed motions. Technically, we require that the ratio of total events to external events is small. The class of allowed motions is usually specified as the class of pseudo-algebraic motions, in which each KDS certificate can flip between true and false at most a bounded number of times.
•Compactness: A KDS is compact if the size of the certificate set it needs is close to linear in the degrees of freedom of the moving system.
•Locality: A KDS is local if no object participates in too many certificates; this condition makes it easier to re-estimate certificate failure times when an object changes its motion law. (The existence of local KDSs is an intriguing theoretical question for several geometric attribute functions.)
24.4.3The Convex Hull, Revisited
We now briefly describe a KDS for maintaining the convex hull of n points moving around in the plane [1].
The key goal in designing a KDS is to produce a repairable certification of the geometric object we want to track. In the convex hull case it turns out that it is a bit more intuitive to look at the dual problem, that of maintaining the upper (and lower) envelope of a set of moving lines in the plane, instead of the convex hull of the primal points. Such dualities represent a powerful toolkit in computational geometry; readers are referred to any standard computational geometry textbook for details, for example [8]. For simplicity we focus only on the upper envelope of the moving lines from now on; the lower envelope case is entirely symmetric. Using a standard divide-and-conquer approach, we partition our lines into two groups of size roughly n/2 each, and assume that recursive invocations of the algorithm maintain the upper envelopes of these groups. For convenience call the groups red and blue.
In order to produce the upper envelope of all the lines, we have to merge the upper envelopes of the red and blue groups and also certify this merge, so we can detect when it ceases to be valid as the lines move; see Figure 24.4.
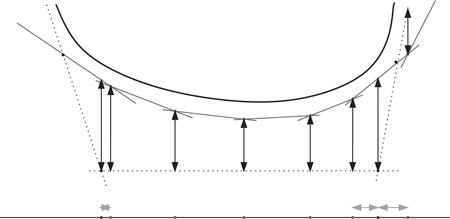
Figure 24.4Merging the red and blue upper envelopes. In this example, the red envelope (solid line) is above the blue (dotted line), except at the extreme left and right areas. Vertical double-ended arrows represent y-certificates and horizontal double-ended arrows represent x-certificates, as described below.
Conceptually, we can approach this problem by sweeping the envelopes with a vertical line from left to right. We advance to the next red (blue) vertex and determine if it is above or below the corresponding blue (red) edge, and so on. In this process we determine when red is above blue or vice versa, as well as when the two envelopes cross. By stitching together all the upper pieces, whether red or blue, we get a representation of the upper envelope of all the lines.
The certificates used in certifying the above merge are of three flavors:
•x-certificates (<x) are used to certify to x-ordering among the red and blue vertices; these involve four original lines.
•y-certificates (<y) are used to certify that a vertex is above or below an edge of the opposite color; these involve three original lines and are exactly the duals of the ccw certificates discussed earlier.
•s-certificates (<s) are slope comparisons between pairs of original lines; though these did not arise in our sweep description above, they are needed to make the KDS local [1].
Figure 24.5 shows examples of how these types of certificates can be used to specify x-ordering constraints and to establish intersection or non-intersection of the envelopes.
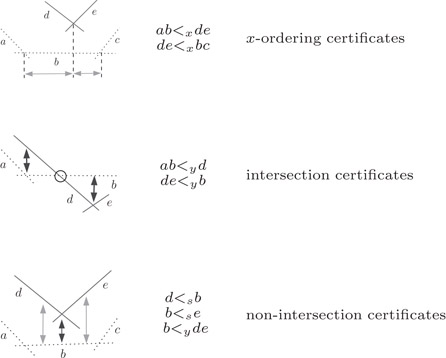
Figure 24.5Using the different types of certificates to certify the red-blue envelope merge.
A total of O(n) such certificates suffices to verify the correctness of the upper envelope merge.
Whenever the motion of the lines causes one of these certificates to fail, a local, constant-time process suffices to update the envelope and repair the certification. Figure 24.6 shows an example where an y-certificate fails, allowing the blue envelope to poke up above the red.
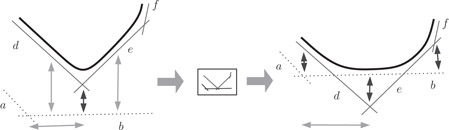
Figure 24.6Envelope repair after a certificate failure. In the event shown lines b, d, and e become concurrent, producing a red-blue envelope intersection
It is straightforward to prove that this kinetic upper envelope algorithm is responsive, local, and compact, using the logarithmic depth of the hierarchical structure of the certification. In order to bound the number of events processed, however, we must assume that the line motions are polynomial or at least pseudo-algebraic. A proof of efficiency can be developed by extruding the moving lines into space-time surfaces. Using certain well-known theorems about the complexity of upper envelopes of surfaces [9] and the overlays of such envelopes [10] it can be shown that in the worst case the number of events processed by this algorithm is near quadratic (O(n2+ε)). Since the convex hull of even linearly moving points can change Ω(n2) times [11], the efficiency result follows.
No comparable structure is known for the convex hull of points in dimensions d ≥ 3.
Even though we have presented kinetic data structures in a geometric setting, there is nothing intrinsically geometric about KDS. The idea of cached assertions that help track an attribute of interest can be applied to many other settings where there is continuous evolution over time punctuated by discrete events, beyond motion in the physical world. For example, consider a graph whose edge weights or capacities are functions of time, as might arise in an evolving communications network. Then the problem of tracking various substructures of interest, such as the minimum spanning tree (MST) of the graph, or a shortest path tree form a source node, can be formulated and studied within the KDS framework.
We present below a quick summary of some of the areas to which kinetic data structures have been applied so far. The are mostly geometric in nature, but several non-geometric examples appear as well.
A number of the original problems for which kinetic data structures were developed are aimed at different measures of how “spread out” a moving set of points in is—one example is the convex hull, whose maintenance was discussed in the previous subsection. Other measures of interest include the diameter, width, and smallest area or perimeter bounding rectangle for a moving set S of n points. All these problems can be solved using the kinetic convex hull algorithm above; the efficiency of the algorithms is O(n2+ε), for any ε > 0. There are also corresponding Ω(n2) lower bounds for the number of combinatorial changes in these measures. Surprisingly, the best known upper bound for maintaining the smallest enclosing disk containing S is still near-cubic. Extensions of these results to dimensions higher than two are also lacking.
These costs can be dramatically reduced if we consider approximate extent measures. If we are content with (1 + ε) approximations to the measures, then an approximate smallest orthogonal rectangle, diameter, and smallest enclosing disk can be maintained with a number of events that is a function ε only and not of n [12]. For example, the bound of the number of approximate diameter updates in under linear motion of the points is O(1/ε).
The fundamental proximity structures in computational geometry are the Voronoi Diagram and the Delaunay triangulation (Chapters 65 and 66). The edges of the Delaunay triangulation contain the closest pair of points, the closest neighbor to each point, as well as a wealth of other proximity information among the points. From the kinetic point of view, these are nice structures, because they admit completely local certifications. Delaunay’s 1934 theorem [13] states that if a local empty sphere condition is valid for each (d − 1)-simplex in a triangulation of points in , then that triangulation must be Delaunay. This makes it simple to maintain a Delaunay triangulation under point motion: an update is necessary only when one of these empty sphere conditions fails. Furthermore, whenever that happens, a local retiling of space (of which the classic “edge-flip” in R2 is a special case) easily restores Delaunayhood. Thus the KDS for Delaunay (and Voronoi) that follows from this theorem is both responsive and efficient—in fact, each KDS event is an external event in which the structure changes. Though no redundant events happen, an exact upper bound for the total number of such events in the worst-case is still elusive even in R2, where the best known upper bound is nearly cubic, while the best lower bound only quadratic [14].
This principle of a set of easily checked local conditions that implies a global property has been used in kinetizing other proximity structures as well. For instance, in the power diagram [15] of a set of disjoint balls, the two closest balls must be neighbors [16]—and this diagram can be kinetized by a similar approach. Voronoi diagrams of more general objects, such as convex polytopes, have also been investigated. For example, in R2 [17] shows how to maintain a compact Voronoi-like diagram among moving disjoint convex polygons; again, a set of local conditions is derived which implies the global correctness of this diagram. As the polygons move, the structure of this diagram allows one to know the nearest pair of polygons at all times.
In many applications the exact L2-distance between objects is not needed and more relaxed notions of proximity suffice. Polyhedral metrics (such as L1 or L∞) are widely used, and the normal unit ball in L2 can be approximated arbitrarily closely by polyhedral approximants. It is more surprising, however, that if we partition the space around each point into a set of polyhedral cones and maintain a number of directional nearest neighbors to each point in each cone, then we can still capture the globally closest pair of points in the L2 metric. By directional neighbors here we mean that we measure distance only along a given direction in that cone. This geometric fact follows from a packing argument and is exploited in Reference 18 to give a different method for maintaining the closest pair of points in . The advantage of this method is that the kinetic events are changes of the sorted order of the points along a set of directions fixed a priori, and therefore the total number of events is provably quadratic.
24.5.3Triangulations and Tilings
Many areas in scientific computation and physical modeling require the maintenance of a triangulation (or more generally a simplicial complex) that approximates a manifold undergoing deformation. The problem of maintaining the Delaunay triangulation of moving points in the plane mentioned above is a special case. More generally, local re-triangulations are necessitated by collapsing triangles, and sometimes required in order to avoid undesirably “thin” triangles. In certain cases the number of nodes (points) may also have to change in order to stay sufficiently faithful to the underlying physical process; see, for example, [19]. Because in general a triangulation meeting certain criteria is not unique or canonical, it becomes more difficult to assess the efficiency of kinetic algorithms for solving such problems. The lower-bound results in Reference 20 indicate that one cannot hope for a subquadratic bound on the number of events in the worst case in the maintenance an any triangulation, even if a linear number of additional Steiner points is allowed.
There is large gap between the desired quadratic upper bound and the current state of art. Even for maintaining an arbitrary triangulation of a set of n points moving linearly in the plane, the best-known algorithm processes O(n7/3) events [21] in the worst case. The algorithm actually maintains a pseudotriangulation of the convex hull of the point set and then a triangulation of each pseudotriangle. Although there are only O(n2) events in the pseudotriangulation, some of the events change too many triangles because of high-degree vertices. Unless additional Steiner points are allowed, there are point configurations for which high-degree vertices are inevitable and therefore some of the events will be expensive. A more clever, global argument is needed to prove a near-quadratic upper bound on the total number of events in the above algorithm. Methods that choose to add additional points, on the other hand, have the burden of defining appropriate trajectories for these Steiner points as well. Finally, today no triangulation that guarantees certain quality on the shapes of triangles as well as a subcubic bound on the number of retiling events is known.
Kinetic methods are naturally applicable to the problem of collision detection between moving geometric objects. Typically collisions occur at irregular intervals, so that fixed-time stepping methods have difficulty selecting an appropriate sampling rate to fit both the numerical requirements of the integrator as well as those of collision detection. A kinetic method based on the discrete events that are the failures of relevant geometric conditions can avoid the pitfalls of both oversampling and undersampling the system. For two moving convex polygons in the plane, a kinetic algorithm where the number of events is a function of the relative separation of the two polygons is given in Reference 22. The algorithm is based on constructing certain outer hierarchies on the two polygons. Analogous methods for 3D polytopes were presented in Reference 23, together with implementation data.
A tiling of the free space around objects can serve as a proof of non-intersection of the objects. If such a tiling can be efficiently maintained under object motion, then it can be the basis of a kinetic algorithm for collision detection. Several papers have developed techniques along these lines, including the case of two moving simple polygons in the plane [24], or multiple moving polygons [21,25]. These developments all exploit deformable pseudotriangulations of the free space—tilings which undergo fewer combinatorial changes than, for example, triangulations. An example from Reference 21 is shown in Figure 24.7. The figure shows how the pseudotriangulation adjusts by local retiling to the motion of the inner quadrilateral. The approach of [21] maintains a canonical pseudotriangulation, while others are based on letting a pseudotriangulation evolve according to the history of the motion. It is unclear at this point which is best. An advantage of all these methods is that the number of certificates needed is close to size of the min-link separating subdivision of the objects, and thus sensitive to how intertwined the objects are.
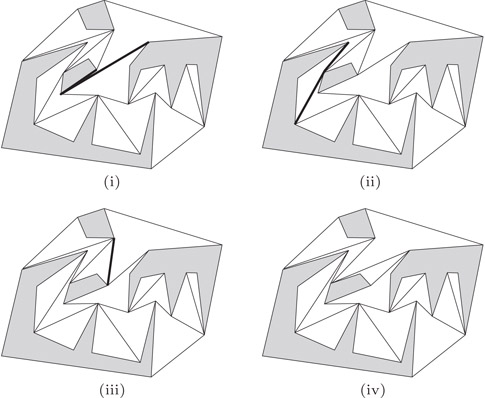
Figure 24.7Snapshots of the mixed pseudotriangulation of [21]. As the center trapezoid-like polygon moves to the right, the edges corresponding to the next about-to-fail certificate are highlighted.
Deformable objects are more challenging to handle. Classical methods, such as bounding volume hierarchies [26], become expensive, as the fixed object hierarchies have to be rebuilt frequently. One possibility for mitigating this cost is to let the hierarchies themselves deform continuously, by having the bounding volumes defined implicitly in terms of object features. Such an approach was developed for flexible linear objects (such as rope or macromolecules), using combinatorially defined sphere hierarchies in Reference 27. In that work a bounding sphere is defined not in the usual way, via its center and radius, but in an implicit combinatorial way, in terms of four feature points of the enclosed object geometry. As the object deforms these implicitly defined spheres automatically track their assigned features, and therefore the deformation. Of course the validity of the hierarchy has to be checked at each time step and repaired if necessary. What helps here is that the implicitly defined spheres change their combinatorial description rather infrequently, even under extreme deformation. An example is shown in Figure 24.8 where the rod shown is bent substantially, yet only the top-level sphere needs to update its description.
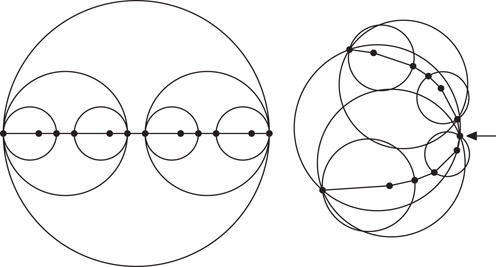
Figure 24.8A thin rod bending from a straight configuration, and a portion of its associated bounding sphere hierarchy. The combinatorially defined sphere hierarchy is stable under deformation. Only the top level sphere differs between the two conformations.
The pseudotriangulation-based methods above can also be adapted to deal with object deformation.
24.5.5Connectivity and Clustering
Closely related to proximity problems is the issue of maintaining structures encoding connectivity among moving geometric objects. Connectivity problems arise frequently in ad hoc mobile communication and sensor networks, where the viability of links may depend on proximity or direct line-of-sight visibility among the stations desiring to communicate. With some assumptions, the communication range of each station can be modeled by a geometric region, so that two stations can establish a link if and only if their respective regions overlap. There has been work on kinetically maintaining the connected components of the union of a set of moving geometric regions for the case of rectangles [28] and unit disks [29].
Clustering mobile nodes is an essential step in many algorithms for establishing communication hierarchies, or otherwise structuring ad hoc networks. Nodes in close proximity can communicate directly, using simpler protocols; correspondingly, well-separated clusters can reuse scarce resources, such the same frequency or time-division multiplexing communication scheme, without interference. Maintaining clusters of mobile nodes requires a tradeoff between the tightness, or optimality of the clustering, and its stability under motion. In Reference 30 a randomized clustering scheme is discussed based on an iterated leader-election algorithm that produces a number of clusters within a constant factor of the optimum, and in which the number of cluster changes is also asymptotically optimal. This scheme was used in Reference 31 to maintain a routing graph on mobile nodes that is always sparse and in which communication paths exist that are nearly as good as those in the full communication graph.
Another fundamental kinetic question is the maintenance of a minimum spanning tree (MST) among n mobile points in the plane, closely related to earlier work on parametric spanning trees [32] in a graph whose edge weights are functions of a parameter λ (λ is time in the kinetic setting). Since the MST is determined by the sorted order of the edge weights in the graph, a simple algorithm can be obtained by maintaining the sorted list of weights and some auxiliary data structures (such an algorithm is quadratic in the graph size, or O(n4) in our case). This was improved when the weights are linear functions of time to nearly O(n11/6) (subquadratic) for planar graphs or other minor-closed families [33]. When the weights are the Euclidean distances between moving points, only approximation algorithms are known and the best event bounds are nearly cubic [18]. For many other optimization problems on geometric graphs, such as shortest paths for example, the corresponding kinetic questions are wide open.
The problem of maintaining the visible parts of the environment when an observer is moving is one of the classic questions in computer graphics and has motivated significant developments, such as binary space partition trees, the hardware depth buffer, etc. The difficulty of the question increases significantly when the environment itself includes moving objects; whatever visibility structures accelerate occlusion culling for the moving observer, must now themselves be maintained under object motion.
Binary space partitions (BSP) are hierarchical partitions of space into convex tiles obtained by performing planar cuts (Chapter 21). Tiles are refined by further cuts until the interior of each tile is free of objects or contains geometry of limited complexity. Once a BSP tree is available, a correct visibility ordering for all geometry fragments in the tiles can be easily determined and incrementally maintained as the observer moves. A kinetic algorithm for visibility can be devised by maintaining a BSP tree as the objects move. The key insight is to certify the correctness of the BSP tree through certain combinatorial conditions, whose failure triggers localized tree rearrangements—most of the classical BSP construction algorithms do not have this property. In , a randomized algorithm for maintaining a BSP of moving disjoint line segments is given in Reference 34. The algorithm processes O(n2) events, the expected cost per tree update is O(log n), and the expected tree size is O(n log n). The maintenance cost increases to O(nλs+2(n) log2n) [35] for disjoint moving triangles in (s is a constant depending on the triangle motion). Both of these algorithms are based on variants on vertical decompositions (many of the cuts are parallel to a given direction). It turns out that in practice these generate “sliver-like” BSP tiles that lead to robustness issues [36].
As the pioneering work on the visibility complex has shown [37], another structure that is well suited to visibility queries in is an appropriate pseudotriangulation. Given a moving observer and convex moving obstacles, a full radial decomposition of the free space around the observer is quite expensive to maintain. One can build pseudotriangulations of the free space that become more and more like the radial decomposition as we get closer to the observer. Thus one can have a structure that compactly encodes the changing visibility polygon around the observer, while being quite stable in regions of the free space well-occluded from the observer [38].
We summarize in Figure 24.9 the efficiency bounds on the main KDSs discussed above.
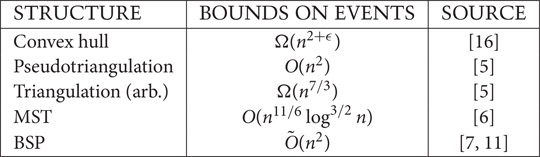
Figure 24.9Bounds on the number of combinatorial changes.
As mentioned above, we still lack efficient kinetic data structures for many fundamental geometric questions. Here is a short list of such open problems:
1.Find an efficient (and responsive, local, and compact) KDS for maintaining the convex hull of points moving in dimensions d ≥ 3.
2.Find an efficient KDS for maintaining the smallest enclosing disk in d ≥ 2. For d = 2, a goal would be an O(n2+ε) algorithm.
3.Establish tighter bounds on the number of Voronoi diagram events, narrowing the gap between quadratic and near-cubic.
4.Obtain a near-quadratic bound on the number of events maintaining an arbitrary triangulation of linearly moving points.*
5.Maintain a kinetic triangulation with a guarantee on the shape of the triangles, in subcubic time.
6.Find a KDS to maintain the MST of moving points under the Euclidean metric achieving subquadratic bounds.
Beyond specific problems, there are also several important structural issues that require further research in the KDS framework. These include:
24.5.8.1Recovery after Multiple Certificate Failures
We have assumed up to now that the KDS assertion cache is repaired after each certificate failure. In many realistic scenarios, however, it is impossible to predict exactly when certificates will fail because explicit motion descriptions may not be available. In such settings we may need to sample the system and thus we must be prepared to deal with multiple (but hopefully few) certificate failures at each time step. A general area of research that this suggests is the study of how to efficiently update common geometric structures, such as convex hulls, Voronoi and Delaunay diagrams, arrangements, etc., after “small motions” of the defining geometric objects.
There is also a related subtlety in the way that a KDS assertion cache can certify the value, or a computation yielding the value, of the attribute of interest. Suppose our goal is to certify that a set of moving points in the plane, in a given circular order, always form a convex polygon. A plausible certificate set for convexity is that all interior angles of the polygon are convex. See Figure 24.10. In the normal KDS setting where we can always predict accurately the next certificate failure, it turns out that the above certificate set is sufficient, as long as at the beginning of the motion the polygon was convex. One can draw, however, nonconvex self-intersecting polygons all of whose interior angles are convex, as also shown in the same figure. The point here is that a standard KDS can offer a historical proof of the convexity of the polygon by relying on the fact that the certificate set is valid and that the polygon was convex during the prior history of the motion. Indeed the counterexample shown cannot arise under continuous motion without one of the angle certificates failing first. On the other hand, if an oracle can move the points when “we are not looking,” we can wake up and find all the angle certificates to be valid, yet our polygon need not be convex. Thus in this oracle setting, since we cannot be sure that no certificates failed during the time step, we must insist on absolute proofs—certificate sets that in any state of the world fully validate the attribute computation or value.
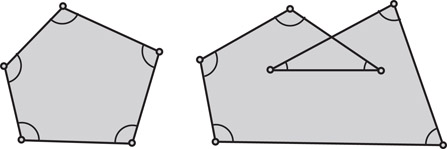
Figure 24.10Certifying the convexity of a polygon.
24.5.8.2Hierarchical Motion Descriptions
Objects in the world are often organized into groups and hierarchies and the motions of objects in the same group are highly correlated. For example, though not all points in an elastic bouncing ball follow exactly the same rigid motion, the trajectories of nearby points are very similar and the overall motion is best described as the superposition of a global rigid motion with a small local deformation. Similarly, the motion of an articulated figure, such as a man walking, is most succinctly described as a set of relative motions, say that of the upper right arm relative to the torso, rather than by giving the trajectory of each body part in world coordinates.
What both of these examples suggest is that there can be economies in motion description, if the motion of objects in the environment can be described as a superposition of terms, some of which can be shared among several objects. Such hierarchical motion descriptions can simplify certificate evaluations, as certificates are often local assertions concerning nearby objects, and nearby objects tend to share motion components. For example, in a simple articulated figure, we may wish to assert CCW (A, B, C) to indicate that an arm is not fully extended, where and are the upper and lower parts of the arm respectively. Evaluating this certificate is clearly better done in the local coordinate frame of the upper arm than in a world frame—the redundant motions of the legs and torso have already been factored out.
24.5.8.3Motion Sensitivity
As already mentioned, the motions of objects in the world are often highly correlated and it behooves us to find representations and data structures that exploit such motion coherence. It is also important to find mathematical measures that capture the degree of coherence of a motion and then use this as a parameter to quantify the performance of motion algorithms. If we do not do this, our algorithm design may be aimed at unrealistic worst-case behavior, without capturing solutions that exploit the special structure of the motion data that actually arise in practice—as already discussed in a related setting in Reference 40. Thus it is important to develop a class of kinetic motion-sensitive algorithms, whose performance can be expressed a function of how coherent the motions of the underlying objects are.
24.5.8.4Non-Canonical Structures
The complexity measures for KDSs mentioned earlier are more suitable for maintaining canonical geometric structures, which are uniquely defined by the position of the data, for example, convex hull, closest pair, and Delaunay triangulation. In these cases the notion of external events is well defined and is independent of the algorithm used to maintain the structure. On the other hand, as we already discussed, suppose we want to maintain a triangulation of a moving point set. Since the triangulation of a point set is not unique, the external events depend on the triangulation being maintained, and thus depend on the algorithm. This makes it difficult to analyze the efficiency of a kinetic triangulation algorithm. Most of the current approaches for maintaining noncanonical structures artificially impose canonicality and maintain the resulting canonical structure. But this typically increases the number of events. So it is entirely possible that methods in which the current form of the structure may depend on its past history can be more efficient. Unfortunately, we lack mathematical techniques for analyzing such history-dependent structures.
Continuous tracking of a geometric attribute may be more than is needed for some applications. There may be time intervals during which the value of the attribute is of no interest; in other scenarios we may be just interested to know the attribute value at certain discrete query times. For example, given n moving points in , we may want to pose queries asking for all points inside a rectangle R at time t, for various values of R and t, or for an interval of time Δt, etc. Such problems can be handled by a mixture of kinetic and static techniques, including standard range-searching tools such as partition trees and range trees [8]. They typically involve tradeoffs between evolving indices kinetically, or prebuilding indices for static snapshots. An especially interesting special case is when we want to be able answer queries about the near future faster than those about the distant future—a natural desideratum in many real-time applications.
A number of other classical range-searching structures, such as k-d-trees and R-trees have recently been investigated for moving objects [41,42].
24.7Sources and Related Materials
Results not given an explicit reference above may be traced in these surveys.
[2]: An early, and by now somewhat dated, survey of KDS work.
[43]: A report based on an NSF-ARO workshop, addressing several issues on modeling motion from the perspective of a variety of disciplines.
[44]: A “popular-science” type article containing material related to the costs of sensing and communication for tracking motion in the real world.
1.J. Basch, L. J. Guibas, and J. Hershberger. Data structures for mobile data. J. Algorithms, 31:1–28, 1999.
2.L. J. Guibas. Kinetic data structures—A state of the art report. In P. K. Agarwal, L. E. Kavraki, and M. Mason, editors. Proc. Workshop Algorithmic Found. Robot., pages 191–209. A. K. Peters, Wellesley, MA, 1998.
3.M. J. Atallah. Some dynamic computational geometry problems. Comput. Math. Appl., 11(12):1171–1181, 1985.
4.P. Gupta, R. Janardan, and M. Smid. Fast algorithms for collision and proximity problems involving moving geometric objects. Comput. Geom. Theory Appl., 6:371–391, 1996.
5.E. Schömer and C. Thiel. Efficient collision detection for moving polyhedra. In Proc. 11th Annu. ACM Sympos. Comput. Geom., pages 51–60, 1995.
6.E. Schömer and C. Thiel. Subquadratic algorithms for the general collision detection problem. In Abstracts 12th European Workshop Comput. Geom., pages 95–101. Universität Münster, 1996.
7.S. Kahan. A model for data in motion. In Proc. 23th Annu. ACM Sympos. Theory Comput., pages 267–277, 1991.
8.M. de Berg, M. van Kreveld, M. Overmars, and O. Schwarzkopf. Comput. Geom.: Algorithms Appl. Springer-Verlag, Berlin, Germany, 2nd edition, 2000.
9.M. Sharir. Almost tight upper bounds for lower envelopes in higher dimensions. Discrete Comput. Geom., 12:327–345, 1994.
10.P. K. Agarwal, O. Schwarzkopf, and M. Sharir. The overlay of lower envelopes and its applications. Discrete Comput. Geom., 15:1–13, 1996.
11.P. K. Agarwal, L. J. Guibas, J. Hershberger, and E. Veach. Maintaining the extent of a moving point set. Discrete Comput. Geom., 26(3):353–374, 2001.
12.P. K. Agarwal and S. Har-Peled. Maintaining approximate extent measures of moving points. In Proc.12th ACM-SIAM Sympos. Discrete Algorithms (SODA), pages 148–157, 2001.
13.B. Delaunay. Sur la sphère vide. A la memoire de Georges Voronoi. Izv. Akad. Nauk SSSR, Otdelenie Matematicheskih i Estestvennyh Nauk, 7:793–800, 1934.
14.G. Albers, L. J. Guibas, J. S. B. Mitchell, and T. Roos. Voronoi diagrams of moving points. Int. J. Comput. Geom. Appl., 8:365–380, 1998.
15.F. Aurenhammer. Power diagrams: Properties, algorithms and applications. SIAM J. Comput., 16:78–96, 1987.
16.L. Guibas and L. Zhang. Euclidean proximity and power diagrams. In Proc. 10-th Canadian Conf. Comput. Geom., pages 90–91, 1998.
17.L. Guibas, J. Snoeyink, and L. Zhang. Compact Voronoi diagrams for moving convex polygons. In Proc. Scand. Workshop on Alg. and Data Structures (SWAT), volume 1851 of Lecture Notes Comput. Sci., pages 339–352. Springer-Verlag, 2000.
18.J. Basch, L. J. Guibas, and L. Zhang. Proximity problems on moving points. In Proc. 13th Annu. ACM Sympos. Comput. Geom., pages 344–351, 1997.
19.H. L. Cheng, T. K. Dey, H. Edelsbrunner, and J. Sullivan. Dynamic skin triangulation. In Proc. 12-th SIAM Symposium on Discrete Algorithms (SODA), pages 47–56, 2001.
20.P. K. Agarwal, J. Basch, M. de Berg, L. J. Guibas, and J. Hershberger. Lower bounds for kinetic planar subdivisions. In Proc. 15-th Annu. ACM Sympos. Comput. Geom. (SoCG), pages 247–254, 1999.
21.P. K. Agarwal, J. Basch, L. J. Guibas, J. Hershberger, and L. Zhang. Deformable free space tiling for kinetic collision detection. In Fourth Workshop Algorithmic Found. Robot., (WAFR), pages 83–96, 2000.
22.J. Erickson, L. J. Guibas, J. Stolfi, and L. Zhang. Separation-sensitive collision detection for convex objects. In Proc. 10-th ACM-SIAM Symp. Discrete Algorithms (SODA), pages 102–111, 1999.
23.L. Guibas, F. Xie, and L. Zhang. Kinetic collision detection: Algorithms and experiments. In Proceedings of the International Conference on Robotics and Automation (ICRA), pages 2903–2910, 2001.
24.J. Basch, J. Erickson, L. J. Guibas, J. Hershberger, and L. Zhang. Kinetic collision detection between two simple polygons. In Proc. 10-th ACM-SIAM Sympos. Discrete Algorithms (SODA), pages 327–336, 1999.
25.D. Kirkpatrick, J. Snoeyink, and B. Speckmann. Kinetic collision detection for simple polygons. In Proc. 16th Annu. ACM Sympos. Comput. Geom., pages 322–330, 2000.
26.S. Gottschalk, M. Lin, and D. Manocha. OBB-Tree: A hierarchical structure for rapid interference detection. In SIGGRAPH 96 Conference Proceedings, pages 171–180, 1996.
27.L. Guibas, A. Nguyen, D. Russell, and L. Zhang. Collision detection for deforming necklaces. In Proc. 18-th Annu. ACM Sympos. Comput. Geom. (SoCG), pages 33–42, 2002.
28.J. Hershberger and S. Suri. Kinetic connectivity of rectangles. In Proc. 15-th Annu. ACM Sympos. Comput. Geom. (SoCG), pages 237–246, 1999.
29.L. Guibas, J. Hershberger, and S. Suri, L. Zhang. Kinetic connectivity for unit disks. In Proc. 16th Annu. ACM Sympos. Comput. Geom., pages 331–340, 2000.
30.J. Gao, L. J. Guibas, J. Hershberger, L. Zhang, and A. Zhu. Discrete mobile centers. In Proc. 17-th ACM Symp. Comput. Geom. (SoCG), pages 190–198, June 2001.
31.J. Gao, L. J. Guibas, J. Hershberger, L. Zhang, and A. Zhu. Geometric spanner for routing in mobile networks. In Proc. 2-nd ACM Symp. on Ad-Hoc Networking and Computing MobiHoc), pages 45–55, October 2001.
32.D. Fernàndez-Baca, G. Slutzki, and D. Eppstein. Using sparsification for parametric minimum spanning tree problems. Nord. J. Comput., 3:352–366, 1996.
33.P. K. Agarwal, D. Eppstein, L. J. Guibas, and M. Henzinger. Parametric and kinetic minimum spanning trees. In Proc. 39th Annu. IEEE Sympos. Found. Comput. Sci., pages 596–605, 1998.
34.P. K. Agarwal, L. J. Guibas, T. M. Murali, and J. S. Vitter. Cylindrical static and kinetic binary space partitions. Comp. Geom.: Theor. Appl., 16:103–127, 2000.
35.P. K. Agarwal, J. Erickson, and L. J. Guibas.Kinetic BSPs for intersecting segments and disjoint triangles. In Proc. 9th ACM-SIAM Sympos. Discrete Algorithms, pages 107–116, 1998.
36.J. L. D. Comba. Kinetic vertical decomposition trees. PhD thesis, Stanford University, 1999.
37.M. Pocchiola and G. Vegter. The visibility complex. Int. J. Comput. Geom. Ap., 6(3):279–308, 1996.
38.O. Hall-Holt. Kinetic visibility. PhD thesis, Stanford University, 2002.
39.P. Agarwal, Y. Wang, and H. Yu. A 2d kinetic triangulation with near quadratic topological changes. In Proc. 20th ACM Symp. Comput. Geom., (SoCG), pages 180–189, 2004.
40.M. de Berg, M. J. Katz, A. F. van der Stappen, and J. Vleugels. Realistic input models for geometric algorithms. In Proc. 13th Annu. ACM Sympos. Comput. Geom., pages 294–303, 1997.
41.P. Agarwal, J. Gao, and L. Guibas. Kinetic medians and kd-trees. In Proc. 10-th Europ. Symp. on Algorithms (ESA), pages 5–16, 2002.
42.P. Agarwal, S. Har-Peled, and M. Procopiuc. Star-tree: An efficent self-adjusting index for moving points. In Workshop on Algorithms Eng., 2002.
43.P. K. Agarwal, L. J. Guibas et al. Algorithmic issues in modeling motion. ACM Comput. Surv., 34(4):550–572, 2003.
44.L. J. Guibas. Sensing, tracking, and reasoning with relations. In IEEE Signal Proc. Magazine, pages 73–85, 2002.
* This chapter has been reprinted from first edition of this Handbook, without any content updates. A version of this chapter has also appeared in the CRC Handbook of Discrete and Computational Geometry (Chapter 50: Modeling Motion), 2nd Edition.
* While this handbook was going to print, Agarwal, Wang and Yu, gave a near-quadratic such algorithm [39].
