Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Optical Waves in Anisotropic Crystals

12
Optical Waves in Anisotropic Crystals

An optical crystal is an anisotopic dielectric and the dielectric tensor of such a crystal in a coordinate system that coincides with the principal axes of the crystal will have zero off-diagonal elements and is given by

(12.1)

ε ¯ = ⎡ ⎣ ⎢ ε 1 00 0 ε 2 0 00 ε 3 ⎤ ⎦ ⎥ .

$\bar{ε} = [\begin{array}{c} ε_{1} & 0 & 0 \\ 0 & ε_{2} & 0 \\ 0 & 0 & ε_{3} \end{array}] .$

The principal refractive indices of the crystal are given by

(12.2)

n j = (ε j ε 0) 1 / 2, j = 1, 2, 3.

$n_{j} = {(\frac{ε_{j}}{ε_{0}})}^{1 / 2}, j = 1, 2, 3.$

The crystals are classified as biaxial, uniaxial, or isotropic depending on the number of equalities involving the principal refractive indices:

(12.3)

n 1 \neq n 2 \neq n 3 (biaxial crystal),

$n_{1} \neq n_{2} \neq n_{3} (biaxial crystal),$

(12.4)

n 1 = n 2 = n o, n 3 = n e (uniaxial crystal),

$n_{1} = n_{2} = n_{o}, n_{3} = n_{e} (uniaxial crystal),$

(12.5)

n 1 = n 2 = n 3 = n o (isotropic crystal) .

$n_{1} = n_{2} = n_{3} = n_{o} (isotropic crystal) .$

Properties of wave propagation in isotropic crystals are discussed in Chapter 2. In the following section, we discuss wave propagation in crystals in the order of increasing complexity of analysis [1,2,3].

12.1Wave Propagation in a Biaxial Crystal along the Principal Axes

Let the principal axes be aligned along the Cartesian coordinate system. A uniform plane wave with a harmonic variation in space and time given by

(12.6)

f (r, t) = exp [j (ω t - k \cdot r)]

$f (r, t) = exp [j (ω t - k \cdot r)]$

satisfies following equations:

(12.7)

k \times E = ω B,

$k \times E = ω B,$

(12.8)

k \times H = - ω D,

$k \times H = - ω D,$

(12.9)

k \cdot B = 0,

$k \cdot B = 0,$

(12.10)

k \cdot D = 0,

$k \cdot D = 0,$

(12.11)

B = μ 0 H,

$B = μ_{0} H,$

(12.12)

D x = ε 0 n 2 x E x, D y = ε 0 n 2 y E y, D z = ε 0 n 2 z E z .

$D_{x} = ε_{0} n_{x}^{2} E_{x}, D_{y} = ε_{0} n_{y}^{2} E_{y}, D_{z} = ε_{0} n_{z}^{2} E_{z} .$

Equation 12.7, Equation 12.8, Equation 12.9, Equation 12.10, Equation 12.11 and Equation 12.12 are obtained from Maxwell’s equations and the constitutive relation for the crystal. From Equations 12.9 and 12.10, we obtain

(12.13)

B k = D k = 0

$B_{k} = D_{k} = 0$

and from Equations 12.7 and 12.8, we obtain

(12.14)

k \times k \times E = ω (k \times B) = - μ 0 ω 2 D .

$k \times k \times E = ω (k \times B) = - μ_{0} ω^{2} D .$

For the particular case of

(12.15)

k = z ˆ k,

$k = \hat{z} k,$

(12.16)

E = x ˆ E,

$E = \hat{x} E,$

(12.17)

H = y ˆ H,

$H = \hat{y} H,$

we obtain

(12.18)

(- k 2 + μ 0 ε 0 ω 2 n 2 x) E = 0.

$(- k^{2} + μ_{0} ε_{0} ω^{2} n_{x}^{2}) E = 0.$

Therefore, the dispersion relation in this case is given by

(12.19)

k 2 = n 2 x ω 2 μ 0 ε 0 .

$k^{2} = n_{x}^{2} ω^{2} μ_{0} ε_{0} .$

The results obtained in this particular case may be stated in words as follows: the propagation of a wave linearly polarized in the direction of a principal axis and propagating along the direction of another principal axis is similar to that of wave propagation in an isotropic case except that the effective refractive index is given by the refractive index in the direction of polarization.

We next consider an example of change of wave polarization by a biaxial crystal. Let the electric field E of a wave propagating in the z-direction in this crystal, at z = 0, be given by

(12.20)

E (0) = E 0 [x ˆ cos 45 ° + y ˆ sin 45 °], z = 0.

$E (0) = E_{0} [\hat{x} cos 45^{°} + \hat{y} sin 45^{°}], z = 0.$

This wave is linearly polarized at 45° (with the x-axis) in the z = 0 plane. If we consider this wave as a superposition of two waves, one with linear polarization in the x-direction and another with linear polarization in the y-direction, then we can write the electric field of this wave at z = d as

(12.21)

E (d) = x ˆ E 0 cos 45 ° exp [j (ω t - n x k 0 d)] + y ˆ E 0 sin 45 ° exp [j (ω t - n y k 0 d)] .

$E (d) = \hat{x} E_{0} cos 45^{°} exp [j (ω t - n_{x} k_{0} d)] + \hat{y} E_{0} sin 45^{°} exp [j (ω t - n_{y} k_{0} d)] .$

Note that the phase of the wave changes with d since n_xk₀d ≠ n_yk₀d. Hence, the wave polarization will not remain linear.

12.2Propagation in an Arbitrary Direction

The notation and the formulations in Section 12.2, Section 12.3 and Section 12.4 closely follow that of reference [3]. Let the unit vector in the direction of propagation be designated by eˆ3 ${\hat{e}}_{3}$ (see Figure 12.1):

(12.22)

k = e ˆ 3 k .

$k = {\hat{e}}_{3} k .$

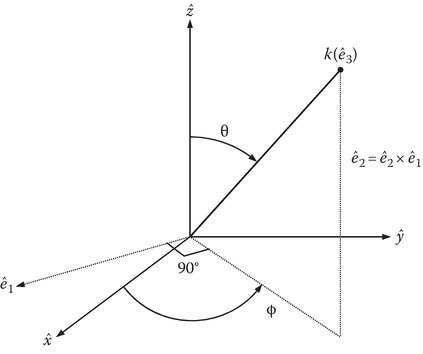
FIGURE 12.1
Orthogonal coordinate system with one coordinate along the wave normal.

Let eˆ1 ${\hat{e}}_{1}$ be a unit vector in the x–y-plane. The direction of eˆ1 ${\hat{e}}_{1}$ is obtained by rotating the projection of eˆ3 ${\hat{e}}_{3}$ in the x–y-plane by 90° as shown in the figure. It is obvious that

(12.23)

e ˆ 3 \cdot e ˆ 1 = 0

${\hat{e}}_{3} \cdot {\hat{e}}_{1} = 0$

and

(12.24)

e ˆ 1 = (e ˆ 1 \cdot x ˆ) x ˆ + (e ˆ 1 \cdot y ˆ) y ˆ = cos (90 - ϕ) x ˆ + cos (180 - ϕ) y ˆ = x ˆ sin ϕ - y ˆ cos ϕ .

${\hat{e}}_{1} = ({\hat{e}}_{1} \cdot \hat{x}) \hat{x} + ({\hat{e}}_{1} \cdot \hat{y}) \hat{y} = cos (90 - ϕ) \hat{x} + cos (180 - ϕ) \hat{y} = \hat{x} sin ϕ - \hat{y} cos ϕ .$

Let

(12.25)

e ˆ 2 = e ˆ 3 \times e ˆ 1 = x ˆ cos θ cos ϕ + y ˆ cos θ sin ϕ - z ˆ sin θ .

${\hat{e}}_{2} = {\hat{e}}_{3} \times {\hat{e}}_{1} = \hat{x} cos θ cos ϕ + \hat{y} cos θ sin ϕ - \hat{z} sin θ .$

The unit vectors eˆ1,eˆ2,andeˆ3 ${\hat{e}}_{1}, {\hat{e}}_{2}, and {\hat{e}}_{3}$ are mutually orthogonal. A vector A may be resolved along x–y–z coordinates as well as along the directions of eˆ1,eˆ2,andeˆ3 ${\hat{e}}_{1}, {\hat{e}}_{2}, and {\hat{e}}_{3}$ . In the latter case, let us designate the vector by A_k with components A₁, A₂, and A₃. The transformation that relates the components of A with components of A_k may be written as

(12.26)

A k = T ¯ ¯ ¯ \cdot A,

$A_{k} = \bar{T} \cdot A,$

(12.27)

A = T ¯ ¯ ¯ - 1 \cdot A k .

$A = {\bar{T}}^{- 1} \cdot A_{k} .$

The transformation is easily determined by noting

(12.28)

A 1 = e ˆ 1 \cdot A k = e ˆ 1 \cdot x ˆ A x + e ˆ 1 \cdot y ˆ A y + e ˆ 1 \cdot z ˆ A z = A x sin ϕ - A y cos ϕ .

$A_{1} = {\hat{e}}_{1} \cdot A_{k} = {\hat{e}}_{1} \cdot \hat{x} A_{x} + {\hat{e}}_{1} \cdot \hat{y} A_{y} + {\hat{e}}_{1} \cdot \hat{z} A_{z} = A_{x} sin ϕ - A_{y} cos ϕ .$

Similar considerations will lead to the determination of the transformation matrix T¯¯¯ $\bar{T}$ :

(12.29)

T ¯ ¯ ¯ = ⎡ ⎣ ⎢ sin ϕ cos θ cos ϕ sin θ cos ϕ - cos ϕ cos θ sin ϕ sin θ sin ϕ 0 - sin θ cos θ ⎤ ⎦ ⎥ .

$\bar{T} = [\begin{array}{c} sin ϕ & - cos ϕ & 0 \\ cos θ cos ϕ & cos θ sin ϕ & - sin θ \\ sin θ cos ϕ & sin θ sin ϕ & cos θ \end{array}] .$

By calculating T¯¯¯−1 ${\bar{T}}^{- 1}$ , we can show that

(12.30)

T ¯ ¯ ¯ - 1 = (T ¯ ¯ ¯) T,

${\bar{T}}^{- 1} = {(\bar{T})}^{T},$

where the superscript T stands for the transpose operation. Defining an impermittivity tensor η¯ $\bar{η}$ (here η¯ $\bar{η}$ is not characteristic impedance),

(12.31)

η = ε - 1 p,

$η = ε_{p}^{- 1},$

where

(12.32)

ε ¯ = ε 0 ε ¯ p,

$\bar{ε} = ε_{0} {\bar{ε}}_{p},$

we obtain

(12.33)

E = 1 ε 0 η ¯ \cdot D,

$E = \frac{1}{ε_{0}} \bar{η} \cdot D,$

(12.34)

T ¯ ¯ ¯ - 1 \cdot E k = 1 ε 0 η ¯ \cdot T ¯ ¯ ¯ - 1 \cdot D k,

${\bar{T}}^{- 1} \cdot E_{k} = \frac{1}{ε_{0}} \bar{η} \cdot {\bar{T}}^{- 1} \cdot D_{k},$

(12.35)

E k = 1 ε 0 [T ¯ ¯ ¯ \cdot η ¯ \cdot T ¯ ¯ ¯ - 1] \cdot D ¯ ¯ ¯ k,

$E_{k} = \frac{1}{ε_{0}} [\bar{T} \cdot \bar{η} \cdot {\bar{T}}^{- 1}] \cdot {\bar{D}}_{k},$

(12.36)

E ¯ ¯ k = 1 ε 0 η ¯ k \cdot D ¯ ¯ ¯ k .

${\bar{E}}_{k} = \frac{1}{ε_{0}} {\bar{η}}_{k} \cdot {\bar{D}}_{k} .$

If the elements of η¯k ${\bar{η}}_{k}$ are designated by η_ij, then Equation 12.33 may be written as

(12.37)

⎡ ⎣ ⎢ E 1 E 2 E 3 ⎤ ⎦ ⎥ = 1 ε 0 ⎡ ⎣ ⎢ η 11 η 21 η 31 η 12 η 22 η 32 η 13 η 23 η 33 ⎤ ⎦ ⎥ ⎡ ⎣ ⎢ D 1 D 2 0 ⎤ ⎦ ⎥ .

$[\begin{array}{c} E_{1} \\ E_{2} \\ E_{3} \end{array}] = \frac{1}{ε_{0}} [\begin{array}{c} η_{11} & η_{12} & η_{13} \\ η_{21} & η_{22} & η_{23} \\ η_{31} & η_{32} & η_{33} \end{array}] [\begin{array}{c} D_{1} \\ D_{2} \\ 0 \end{array}] .$

From Equations 12.7, 12.8, and 12.37, we obtain

(12.38)

ω B 2 = k E 1 = k ε 0 [η 11 D 1 + η 12 D 2],

$ω B_{2} = k E_{1} = \frac{k}{ε_{0}} [η_{11} D_{1} + η_{12} D_{2}],$

(12.39)

ω B 1 = - k E 2 = - k ε 0 [η 21 D 1 + η 22 D 2],

$ω B_{1} = - k E_{2} = - \frac{k}{ε_{0}} [η_{21} D_{1} + η_{22} D_{2}],$

(12.40)

ω D 2 = - k H 1 = - k B 1 μ 0,

$ω D_{2} = - k H_{1} = - \frac{k B_{1}}{μ_{0}},$

(12.41)

ω D 1 = k H 2 = k B 2 μ 0 .

$ω D_{1} = k H_{2} = \frac{k B_{2}}{μ_{0}} .$

By eliminating all other variables, we can obtain the dispersion relation

(12.42)

⎡ ⎣ η 11 - u 2 c 2 η 21 η 12 η 22 - u 2 c 2 ⎤ ⎦ [D 1 D 2] = 0,

$[\begin{array}{c} η_{11} - \frac{u^{2}}{c^{2}} & η_{12} \\ η_{21} & η_{22} - \frac{u^{2}}{c^{2}} \end{array}] [\begin{array}{c} D_{1} \\ D_{2} \end{array}] = 0,$

where u = ω/k is the phase velocity.

12.3Propagation in an Arbitrary Direction: Uniaxial Crystal

As an example of further calculations, we restrict ourselves to a uniaxial crystal. For this case,

(12.43)

η ¯ k = ⎡ ⎣ ⎢ η 00 0 η cos 2 θ + η z sin 2 θ (η - η z) sin θ cos θ 0 (η - η z) sin θ cos θ η sin θ + η z cos θ ⎤ ⎦ ⎥,

${\bar{η}}_{k} = [\begin{array}{c} η & 0 & 0 \\ 0 & η {cos}^{2} θ + η_{z} {sin}^{2} θ & (η - η_{z}) sin θ cos θ \\ 0 & (η - η_{z}) sin θ cos θ & η sin θ + η_{z} cos θ \end{array}],$

where

(12.44)

η = 1 n 2 o,

$η = \frac{1}{n_{o}^{2}},$

(12.45)

η z = 1 n 2 e .

$η_{z} = \frac{1}{n_{e}^{2}} .$

Thus,

(12.46)

η 11 = η,

$η_{11} = η,$

(12.47)

η 12 = η 21 = 0,

$η_{12} = η_{21} = 0,$

(12.48)

η 22 = η cos 2 θ + η z sin 2 θ .

$η_{22} = η {cos}^{2} θ + η_{z} {sin}^{2} θ .$

From Equations 12.42 and Equation 12.46, Equation 12.47 and Equation 12.48, we obtain the following results.

Case 1:

(12.49)

(η - u 2 c 2) = 0 (D 1 \neq 0, D 2 = 0) .

$(η - \frac{u^{2}}{c^{2}}) = 0 (D_{1} \neq 0, D_{2} = 0) .$

Case 2:

(12.50)

η 22 = η cos 2 θ + η z sin 2 θ = u 2 c 2 (D 1 = 0, D 2 \neq 0) .

$η_{22} = η {cos}^{2} θ + η_{z} {sin}^{2} θ = \frac{u^{2}}{c^{2}} (D_{1} = 0, D_{2} \neq 0) .$

In the first case, the phase velocity is

(12.51)

u = \pm c n o (ordinary wave)

$u = \pm \frac{c}{n_{o}} (ordinary wave)$

and in the second case it is

(12.52)

u c = 1 n = cos 2 θ n 2 o + sin 2 θ n 2 e - - - - - - - - - - - - \sqrt (extraordinary wave) .

$\frac{u}{c} = \frac{1}{n} = \sqrt{\frac{{cos}^{2} θ}{n_{o}^{2}} + \frac{{sin}^{2} θ}{n_{e}^{2}}} (extraordinary wave) .$

In the latter case, the phase velocity depends on θ.

12.4k-Surface

Let k be the scalar wave number and is given by

(12.53)

k z = k cos θ,

$k_{z} = k cos θ,$

(12.54)

$k_{s} = k sin θ,$

where k_s is the transverse wave number.

For Case 1,

(12.55)

$u = \frac{c}{n_{o}} = \frac{ω}{k},$

(12.56)

$k_{z}^{2} + k_{s}^{2} = k^{2} = \frac{ω^{2} n_{o}^{2}}{c^{2}} .$

Figure 12.2a shows this circle in k_s − k_z plain.

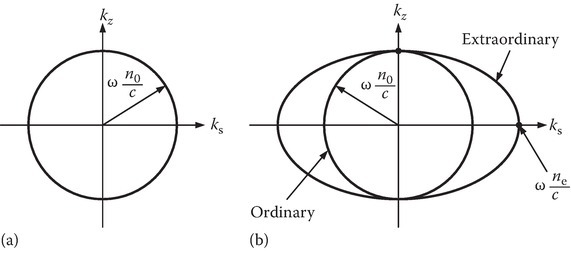
FIGURE 12.2
k-Surface. (a) Ordinary and (b) ordinary and extraordinary.

For Case 2,

(12.57)

$\frac{u^{2}}{c^{2}} = \frac{ω^{2}}{k^{2} c^{2}} = \frac{{cos}^{2} θ}{n_{o}^{2}} + \frac{{sin}^{2} θ}{n_{e}^{2}},$

which may be written as

(12.58)

$\frac{k_{s}^{2}}{n_{e}^{2} (ω^{2} / c^{2})} + \frac{k_{z}^{2}}{n_{o}^{2} (ω^{2} / c^{2})} = 1.$

Thus, the curve in k_s − k_z plane is an ellipse as shown in Figure 12.2.

The phase velocity is given by ω/k and for the ordinary wave it is the same for all θ. For the extraordinary wave, ω/k depends on θ, since the k curve is an ellipse. The group velocity for this case can be defined as a vector:

(12.59)

$u_{g} = \nabla_{k} ω = {\hat{k}}_{s} \frac{\partial ω}{\partial k_{s}} + \hat{z} \frac{\partial ω}{\partial k_{z}} .$

In three-dimensional k-space, we obtain a sphere for the ordinary wave and ellipsoid for the extraordinary wave.

For a uniaxial crystal, the refractive index is the same along the two principal directions (n_o in x- and y-directions in our notation) and different along the axis (n_e along the z-axis) called the optical axis. Note that the refractive index surfaces touch along the k_z-axis.

12.5Group Velocity as a Function of Polar Angle

The angle between the optical axis and the wave normal (direction of phase propagation) is the polar angle θ. From Equation 12.58, we obtain

$ω^{2} = c^{2} [\frac{k_{z}^{2}}{n_{o}^{2}} + \frac{k_{s}^{2}}{n_{e}^{2}}],$

$ω = c {[\frac{k_{z}^{2}}{n_{o}^{2}} + \frac{k_{s}^{2}}{n_{e}^{2}}]}^{1 / 2},$

where c is the velocity of light in free space, k_z = k cos θ, and k_s = k sin θ:

(12.60)

$\frac{\partial ω}{\partial k_{z}} = \frac{c}{2} {[\frac{k_{z}^{2}}{n_{o}^{2}} + \frac{k_{s}^{2}}{n_{e}^{2}}]}^{- 1 / 2} [\frac{2 k_{z}}{n_{o}^{2}}],$

(12.61)

$\frac{\partial ω}{\partial k_{s}} = \frac{c}{2} {[\frac{k_{z}^{2}}{n_{o}^{2}} + \frac{k_{s}^{2}}{n_{e}^{2}}]}^{- 1 / 2} [\frac{2 k_{s}}{n_{e}^{2}}] .$

Noting that

${[\frac{k_{z}^{2}}{n_{o}^{2}} + \frac{k_{s}^{2}}{n_{e}^{2}}]}^{- 1 / 2} = {(\frac{ω^{2}}{c^{2}})}^{- 1 / 2} = \frac{c}{ω},$

$\frac{\partial ω}{\partial k_{z}} = \frac{c}{2} \frac{2 k_{z}}{n_{o}^{2}} \frac{c}{ω} = \frac{k_{z} c^{2}}{ω n_{o}^{2}} = \frac{c^{2} k cos θ}{ω n_{o}^{2}} .$

Similarly,

$\frac{\partial ω}{\partial k_{s}} = \frac{c^{2} k sin θ}{ω n_{e}^{2}},$

(12.62)

$u_{g} = c^{2} \frac{k}{ω} [\frac{sin θ}{n_{e}^{2}} {\hat{a}}_{s} + \frac{cos θ}{n_{o}^{2}} {\hat{a}}_{z}] .$

The magnitude of the group velocity |u_g| is given by

(12.63)

$|u_{g}| = c^{2} \frac{k}{ω} {[\frac{{sin}^{2} θ}{n_{e}^{4}} + \frac{{cos}^{2} θ}{n_{o}^{4}}]}^{1 / 2} .$

Since ω/k = u,

(12.64)

$|u_{g}| u = c^{2} {[\frac{{sin}^{2} θ}{n_{e}^{4}} + \frac{{cos}^{2} θ}{n_{o}^{4}}]}^{1 / 2} .$

If the angle of u_g with the polar axis is θ_g, then

$tan θ_{g} = \frac{u_{gs}}{u_{g z}} = \frac{sin θ / n_{e}^{2}}{cos θ / n_{o}^{2}} = tan θ \frac{n_{o}^{2}}{n_{e}^{2}} .$

If α = θ − θ_g, then

(12.65)

$tan α = tan (θ - θ_{g}) = \frac{tan θ - tan θ_{g}}{1 + tan θ tan θ_{g}} = \frac{(1 - n_{o}^{2} / n_{e}^{2}) tan θ}{1 + (n_{o}^{2} {tan}^{2} θ) / n_{e}^{2}} .$

Note that if θ = 0, then tan α = 0, and α = 0.

If θ = π/2, then tan α = ∞/∞² = 1/∞ = 0, thus α = 0 (Figure 12.3).

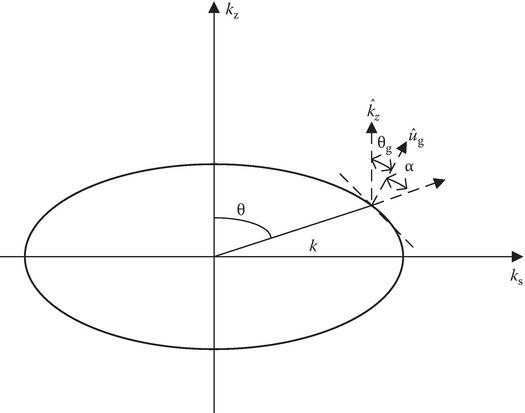
FIGURE 12.3
Various angles for the extraordinary wave.

To find the value of θ so that α is maximum, let tan θ = x, and we have to find x that maximizes $x / (1 + (n_{o}^{2} x^{2}) / n_{e}^{2})$ . Differentiating with respect to x and equating to zero (use νdu − udν = 0), we obtain

$[1 + \frac{n_{o}^{2}}{n_{e}^{2}} x^{2}] - x [\frac{n_{o}^{2}}{n_{e}^{2}} 2 x] = 0,$

$1 - \frac{n_{o}^{2}}{n_{e}^{2}} x^{2} = 0,$

(12.66)

$x = \frac{n_{e}}{n_{o}} .$

α is maximum when tan θ = n_e/n_o:

(12.67)

$\begin{matrix} \tan (α_{\max}) & = & \frac{n_{e} / n_{o} (1 - n_{o}^{2} / n_{e}^{2})}{1 + (n_{o}^{2} / n_{e}^{2}) (n_{e}^{2} / n_{o}^{2})} = \frac{n_{e} / n_{o} - n_{o} / n_{e}}{2} = \frac{n_{e}^{2} - n_{o}^{2}}{2 n_{o} n_{e}} = \frac{(n_{e} + n_{o}) (n_{e} - n_{o})}{2 n_{o} n_{e}}, \\ \tan (α_{\max}) & = & \frac{(n_{e} + n_{o}) (n_{e} - n_{o})}{2 n_{o} n_{e}} . \end{matrix}$

For example, for quartz,

$tan (α_{max}) = \frac{(1.553 + 1.544) (1.553 - 1.544)}{2 (1.553) (1.544)} = 5.812 \times 10^{- 3},$

$α_{max} = {0.333}^{°} .$

A further approximation can be made for the case n_o ≈ n_e.

For n_o ≈ n_e, tan θ ≈ 1 for α to be maximum.

Hence, θ ≈ 45° for α to be maximum.

From Equation 12.67, we obtain

$tan (α_{max}) \approx \frac{2 n_{e} (n_{e} - n_{o})}{2 n_{o} n_{e}} = \frac{n_{e} - n_{o}}{n_{o}} = \frac{Δ n}{n} = \frac{0.009}{1.544} = 5.829 \times 10^{- 3} .$

α_max = 0.334° nearest to the previous answer.

tan (α_max) is proportional to |n_o − n_e|.

12.6Reflection by an Anisotropic Half-Space

When the transmission medium is anisotropic, we have seen that there are two transmitted waves (Figure 12.4). For oblique incidence, each transmitted wave has its own transmission angle. Since the boundary condition is still that k_x is conserved for all waves, Snell’s law may be written as

(12.68)

$k_{x} = k_{o} sin θ_{i} = k_{1} sin θ_{T 1} = k_{2} sin θ_{T 2},$

where k₁ and k₂ are the wave numbers of the respective transmitted waves. We have noted that for the extraordinary wave, the k-surface is not a sphere. In such a case, the value of k depends on the angle of refraction. A graphical interpretation of the technique of obtaining the solution is shown in Figure 12.5.

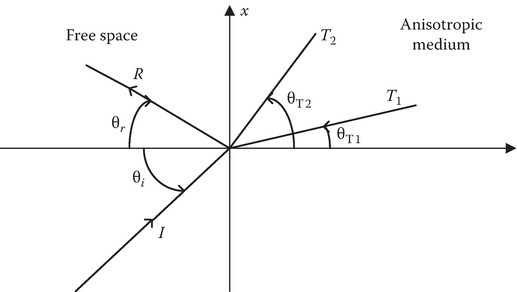
FIGURE 12.4
Reflection and transmission by an anisotropic medium.

FIGURE 12.5
Computation of the angle of transmission.

References

1.Saleh, B.E. A. and Teich, M. C., Fundamentals of Photonics, Wiley, New York, 1991.
2.Yariv, A. and Yeh, P., Optical Waves in Crystals, Wiley, New York, 1984.
3.Kong, J.U., Electromagnetic Wave Theory, Wiley, New York, 1990.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 12. Optical Waves in Anisotropic Crystals

Create new playlist

Sign In

Sign Up

Table of Contents for
12. Optical Waves in Anisotropic Crystals