]>

Appendix 1A: Vector Formulas and Coordinate Systems

Appendix 1A: Vector Formulas and Coordinate Systems

1A.1Vector Transformations

This appendix closely follows the development of the materials given in [1], which is a standard development used in many textbooks. The three coordinate systems, (a) rectangular, (b) cylindrical, and (c) spherical, are shown in Figure 1A.1.

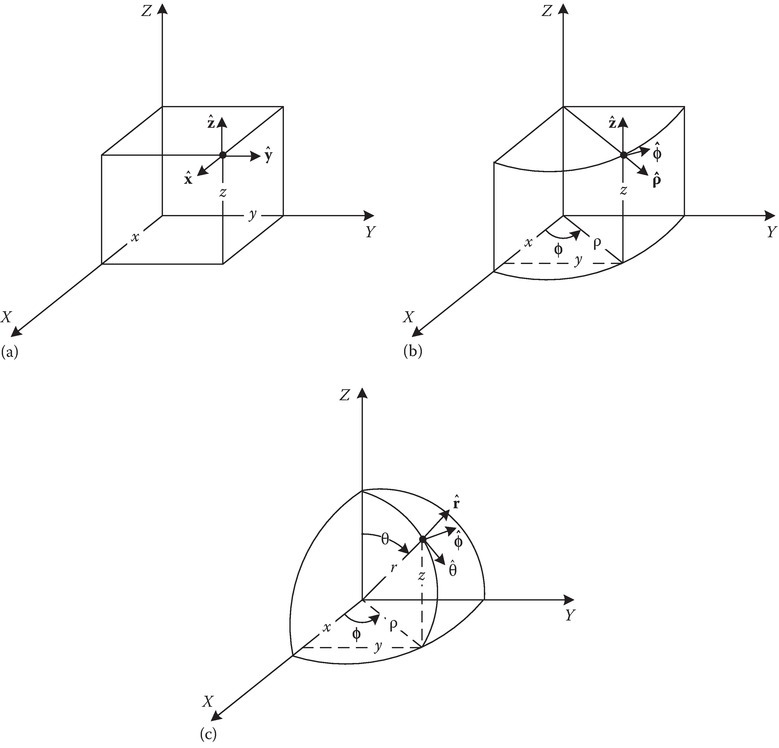
image

FIGURE 1A.1
(a) Rectangular, (b) cylindrical, and (c) spherical coordinate systems.

1A.1.1Rectangular to Cylindrical (and Cylindrical to Rectangular) Transformation

Referring to Figure 1A.1b, the coordinate transformation from rectangular (x, y, z) to cylindrical (ρ, ϕ, z) coordinates is given by

(1A.1)x=ρcosϕ,y=ρsinϕ,z=z.
x=ρcosϕ,y=ρsinϕ,z=z.

In rectangular coordinates, a vector A is written as

(1A.2)A=ˆxAx+ˆyAy+ˆzAz,
A=xˆAx+yˆAy+zˆAz,

where ˆx,ˆy,andˆzxˆ,yˆ,andzˆ are the unit vectors and Ax, Ay, and Az are the components of the vector A in the rectangular coordinate system. We can also write A as

(1A.3)A=ˆρAρ+ˆφAϕ+ˆzAz,
A=ρˆAρ+φˆAϕ+zˆAz,

where ˆρ,ˆφ,andˆzρˆ,φˆ,andzˆ are the unit vectors and Aρ, Aϕ, and Az are the vector components in the cylindrical coordinate system. It can be shown that

(1A.4)ˆx=ˆρcosϕ−ˆφsinϕ,ˆy=ˆρsinϕ+ˆφcosϕ,ˆz=ˆz,
xˆ=ρˆcosϕ−φˆsinϕ,yˆ=ρˆsinϕ+φˆcosϕ,zˆ=zˆ,

and therefore,

(1A.5)A=(ˆρcosϕ−ˆφsinϕ)Ax+(ˆρsinϕ−ˆφcosϕ)Ay+ˆzAz,A=ˆρ(Axcosϕ+Aysinϕ)−ˆφ(Axsinϕ+Aycosϕ)+ˆzAz,
A=(ρˆcosϕ−φˆsinϕ)Ax+(ρˆsinϕ−φˆcosϕ)Ay+zˆAz,A=ρˆ(Axcosϕ+Aysinϕ)−φˆ(Axsinϕ+Aycosϕ)+zˆAz,

thus

(1A.6)Aρ=Axcosϕ+Aysinϕ,Aϕ=−Axsinϕ+Aycosϕ,Az=Az.
Aρ=Axcosϕ+Aysinϕ,Aϕ=−Axsinϕ+Aycosϕ,Az=Az.

This can be expressed in the matrix form as

(1A.7)[AρAϕAz]=[cosϕsinϕ0−sinϕcosϕ0001][AxAyAz]=[A]rc[AxAyAz],
⎡⎣⎢AρAϕAz⎤⎦⎥=⎡⎣⎢cosϕ−sinϕ0sinϕcosϕ0001⎤⎦⎥⎡⎣⎢AxAyAz⎤⎦⎥=[A]rc⎡⎣⎢AxAyAz⎤⎦⎥,

where

(1A.8)[A]rc=[cosϕsinϕ0−sinϕcosϕ0001]
[A]rc=⎡⎣⎢cosϕ−sinϕ0sinϕcosϕ0001⎤⎦⎥

is the transformation matrix for rectangular to cylindrical components. Since [A]rc is an orthonormal matrix (its inverse is equal to its transpose), the transformation matrix from cylindrical to rectangular components can be written as

(1A.9)[A]cr=[A]−1rc=[A]Trc=[cosϕ−sinϕ0sinϕcosϕ0001],
[A]cr=[A]−1rc=[A]Trc=⎡⎣⎢cosϕsinϕ0−sinϕcosϕ0001⎤⎦⎥,
(1A.10)[AxAyAz]=[cosϕ−sinϕ0sinϕcosϕ0001][AρAϕAz],
⎡⎣⎢AxAyAz⎤⎦⎥=⎡⎣⎢cosϕsinϕ0−sinϕcosϕ0001⎤⎦⎥⎡⎣⎢AρAϕAz⎤⎦⎥,
(1A.11)Ax=Aρcosϕ−Aϕsinϕ,Ay=Aρsinϕ+Aϕcosϕ,Az=Az.
Ax=Aρcosϕ−Aϕsinϕ,Ay=Aρsinϕ+Aϕcosϕ,Az=Az.

1A.1.2Cylindrical to Spherical (and Spherical to Cylindrical) Transformation

From Figure 1A.1c, it can be seen that the cylindrical and spherical coordinates are related by

(1A.12)ρ=rsinθ,z=rcosθ.
ρ=rsinθ,z=rcosθ.

In a manner similar to the previous section, it can be shown that

(1A.13)Ar=Aρsinθ+Azcosθ,Aθ=Aρcosθ−Azsinθ,
Ar=Aρsinθ+Azcosθ,Aθ=Aρcosθ−Azsinθ,

therefore

Aϕ=Aϕ,
Aϕ=Aϕ,

or in matrix notation

(1A.14)[ArAθAϕ]=[sinθ0cosθcosθ0−sinθ010][AρAϕAz],
⎡⎣⎢ArAθAϕ⎤⎦⎥=⎡⎣⎢sinθcosθ0001cosθ−sinθ0⎤⎦⎥⎡⎣⎢AρAϕAz⎤⎦⎥,
(1A.15)[A]cs=[sinθ0cosθcosθ0−sinθ010].
[A]cs=⎡⎣⎢sinθcosθ0001cosθ−sinθ0⎤⎦⎥.

The [A]cs matrix is orthonormal and so its inverse is given by

(1A.16)[A]sc=[A]−1cs=[A]Tcs=[sinθcosθ0001cosθ−sinθ0]
[A]sc=[A]−1cs=[A]Tcs=⎡⎣⎢sinθ0cosθcosθ0−sinθ010⎤⎦⎥

and the spherical to cylindrical transformation is accomplished by

(1A.17)[AρAϕAz]=[sinθcosθ0001cosθ−sinθ0][ArAθAϕ],
⎡⎣⎢AρAϕAz⎤⎦⎥=⎡⎣⎢sinθ0cosθcosθ0−sinθ010⎤⎦⎥⎡⎣⎢ArAθAϕ⎤⎦⎥,
(1A.18)Aρ=Arsinθ+Aθcosθ,Aϕ=Aϕ,Az=Arcosθ−Aθsinθ.
Aρ=Arsinθ+Aθcosθ,Aϕ=Aϕ,Az=Arcosθ−Aθsinθ.

1A.1.3Rectangular to Spherical (and Spherical to Rectangular) Transformation

From Figure 1A.1c, it can be seen that the rectangular and spherical coordinates are related by

(1A.19)x=rsinθcosϕ,
x=rsinθcosϕ,

or

y=rsinθsinϕ,x=rcosθ,
y=rsinθsinϕ,x=rcosθ,

and the spherical and rectangular components by

(1A.20)Ar=Axsinθcosϕ+Aysinθsinϕ+Azcosθ,Aθ=Axcosθcosϕ+Aycosθsinϕ−Azsinθ,Aϕ=−Axsinϕ+Aycosϕ.
Ar=Axsinθcosϕ+Aysinθsinϕ+Azcosθ,Aθ=Axcosθcosϕ+Aycosθsinϕ−Azsinθ,Aϕ=−Axsinϕ+Aycosϕ.

In the matrix form,

(1A.21)[ArAθAϕ]=[sinθcosϕsinθsinϕcosθcosθcosϕcosθsinϕ−sinθ−sinϕcosϕ0][AxAyAz],
⎡⎣⎢ArAθAϕ⎤⎦⎥=⎡⎣⎢sinθcosϕcosθcosϕ−sinϕsinθsinϕcosθsinϕcosϕcosθ−sinθ0⎤⎦⎥⎡⎣⎢AxAyAz⎤⎦⎥,
(1A.22)[A]rs=[sinθcosϕsinθsinϕcosθcosθcosϕcosθsinϕ−sinθ−sinϕcosϕ0].
[A]rs=⎡⎣⎢sinθcosϕcosθcosϕ−sinϕsinθsinϕcosθsinϕcosϕcosθ−sinθ0⎤⎦⎥.

The [A]rs matrix is orthonormal and so its inverse is given by

(1A.23)[A]sr=[A]−1rs=[A]Trs=[sinθcosϕcosθcosϕ−sinϕsinθsinϕcosθsinϕcosϕcosθ−sinθ0]
[A]sr=[A]−1rs=[A]Trs=⎡⎣⎢sinθcosϕsinθsinϕcosθcosθcosϕcosθsinϕ−sinθ−sinϕcosϕ0⎤⎦⎥

and the spherical to rectangular transformation is accomplished by

(1A.24)[AxAyAz]=[sinθcosϕcosθcosϕ−sinϕsinθsinϕcosθsinϕcosϕcosθ−sinθ0][ArAθAϕ],
⎡⎣⎢AxAyAz⎤⎦⎥=⎡⎣⎢sinθcosϕsinθsinϕcosθcosθcosϕcosθsinϕ−sinθ−sinϕcosϕ0⎤⎦⎥⎡⎣⎢ArAθAϕ⎤⎦⎥,
(1A.25)Ax=Arsinθcosϕ+Aθcosθcosϕ−Aϕsinϕ,Ay=Arsinθsinϕ+Aθcosθsinϕ+Aϕcosϕ,Az=Arcosθ−Aθsinθ.
Ax=Arsinθcosϕ+Aθcosθcosϕ−Aϕsinϕ,Ay=Arsinθsinϕ+Aθcosθsinϕ+Aϕcosϕ,Az=Arcosθ−Aθsinθ.

1A.2Vector Differential Operators

The differential operators normally include gradient of a scalar (∇ψ), divergence of a vector (∇·A), curl of a vector (∇ × A), Laplacian of a scalar (∇ 2ψ), and Laplacian of a vector (∇ 2A). These will be shown in rectangular, cylindrical, and spherical coordinates as given below.

1A.2.1Rectangular Coordinates

(1A.26)∇ψ=ˆx∂ψ∂x+ˆy∂ψ∂y+ˆz∂ψ∂z,
∇ψ=xˆ∂ψ∂x+yˆ∂ψ∂y+zˆ∂ψ∂z,
(1A.27)∇⋅A=∂Ax∂x+∂Ay∂y+∂Az∂z,
∇⋅A=∂Ax∂x+∂Ay∂y+∂Az∂z,
(1A.28)∇×A=|ˆxˆyˆz∂∂x∂∂y∂∂zAxAyAz|=ˆx(∂Az∂y−∂Ay∂z)+ˆy(∂Ax∂z−∂Az∂x)+ˆz(∂Ay∂x−∂Ax∂y),
∇×A=∣∣∣∣∣xˆ∂∂xAxyˆ∂∂yAyzˆ∂∂zAz∣∣∣∣∣=xˆ(∂Az∂y−∂Ay∂z)+yˆ(∂Ax∂z−∂Az∂x)+zˆ(∂Ay∂x−∂Ax∂y),
(1A.29)∇⋅∇ψ=∇2ψ=∂2ψ∂x2+∂2ψ∂y2+∂2ψ∂z2,
∇⋅∇ψ=∇2ψ=∂2ψ∂x2+∂2ψ∂y2+∂2ψ∂z2,
(1A.30)∇2A=ˆx∇2Ax+ˆy∇2Ay+ˆz∇2Az.
∇2A=xˆ∇2Ax+yˆ∇2Ay+zˆ∇2Az.

1A.2.2Cylindrical Coordinates

(1A.31)∇ψ=ˆρ∂ψ∂ρ+ˆφ1ρ∂ψ∂ϕ+ˆz∂ψ∂z,
∇ψ=ρˆ∂ψ∂ρ+φˆ1ρ∂ψ∂ϕ+zˆ∂ψ∂z,
(1A.32)∇⋅A=1ρ∂∂ρ(ρAρ)+1ρ∂Aϕ∂ϕ+∂Az∂z,
∇⋅A=1ρ∂∂ρ(ρAρ)+1ρ∂Aϕ∂ϕ+∂Az∂z,
(1A.33)∇×A=ˆρ(1ρ∂Az∂ϕ−∂Aϕ∂z)+ˆφ(∂Aρ∂z−∂Az∂ρ)+ˆz(1ρ∂(ρAϕ)∂ρ−1ρ∂Aρ∂ϕ),
∇×A=ρˆ(1ρ∂Az∂ϕ−∂Aϕ∂z)+φˆ(∂Aρ∂z−∂Az∂ρ)+zˆ(1ρ∂(ρAϕ)∂ρ−1ρ∂Aρ∂ϕ),
(1A.34)∇2ψ=1ρ∂∂ρ(ρ∂ψ∂ρ)+1ρ2∂2ψ∂ϕ2+∂2ψ∂z2,
∇2ψ=1ρ∂∂ρ(ρ∂ψ∂ρ)+1ρ2∂2ψ∂ϕ2+∂2ψ∂z2,
(1A.35)∇2A=∇(∇⋅A)−∇×∇×A,
∇2A=∇(∇⋅A)−∇×∇×A,
(1A.36)∇2A=ˆρ(∂2Aρ∂ρ2+1ρ∂Aρ∂ρ−Aρρ2+1ρ2∂2Aρ∂ϕ2−2ρ2∂Aϕ∂ϕ+∂2Aρ∂z2)  +ˆφ(∂2Aϕ∂ρ2+1ρ∂Aϕ∂ρ−Aϕρ2+1ρ2∂2Aϕ∂ϕ2+2ρ2∂Aρ∂ϕ+∂2Aϕ∂z2)  +ˆz(∂2Az∂ρ2+1ρ∂Az∂ρ+1ρ2∂2Az∂ϕ2+∂2Az∂z2).
∇2A=ρˆ(∂2Aρ∂ρ2+1ρ∂Aρ∂ρ−Aρρ2+1ρ2∂2Aρ∂ϕ2−2ρ2∂Aϕ∂ϕ+∂2Aρ∂z2)  +φˆ(∂2Aϕ∂ρ2+1ρ∂Aϕ∂ρ−Aϕρ2+1ρ2∂2Aϕ∂ϕ2+2ρ2∂Aρ∂ϕ+∂2Aϕ∂z2)  +zˆ(∂2Az∂ρ2+1ρ∂Az∂ρ+1ρ2∂2Az∂ϕ2+∂2Az∂z2).

1A.2.3Spherical Coordinates

(1A.37)∇ψ=ˆr∂ψ∂r+ˆθ1r∂ψ∂θ+ˆφ1rsinθ∂ψ∂ϕ,
(1A.38)∇⋅A=1r2∂∂r(r2Ar)+1rsinθ∂∂θ(sinθAθ)+1rsinθ∂Aϕ∂ϕ,
(1A.39)∇×A=ˆrrsinθ(∂∂θ(sinθAϕ)−∂Aθ∂ϕ)+ˆθr(1sinθ∂Ar∂ϕ−∂∂r(rAϕ))+ˆφr(∂∂r(rAθ)−∂Ar∂θ),
(1A.40)∇2ψ=1r2∂∂r(r2∂ψ∂r)+1r2sinθ∂∂θ(sinθ∂ψ∂θ)+1r2sin2θ∂2ψ∂ϕ2,
(1A.41)∇2A=∇(∇⋅A)−∇×∇×A,
(1A.42)∇2A=ˆr(∂2Ar∂r2+2r∂Ar∂r−2r2Ar+1r2∂2Ar∂θ2+cotθr2∂Ar∂θ+1r2sin2θ∂2Ar∂ϕ2−2r2∂Aθ∂θ−2cotθr2Aθ−2r2sinθ∂Aϕ∂ϕ)  +ˆθ(∂2Aθ∂r2+2r∂Aθ∂r−Aθr2sin2θ+1r2∂2Aθ∂θ2+cotθr2∂Aθ∂θ+1r2sin2θ∂2Aθ∂ϕ2+2r2∂Ar∂θ−2cotθr2sinθ∂Aϕ∂ϕ)  +ˆφ(∂2Aϕ∂r2+2r∂Aϕ∂r−1r2sin2θAϕ+1r2∂2Aϕ∂θ2+cotθr2∂Aϕ∂θ+1r2sin2θ∂2Aϕ∂ϕ2+2r2sinθ∂Ar∂ϕ+2cotθr2sinθ∂Aθ∂ϕ).

1A.3Vector Identities

1A.3.1Addition and Multiplication

(1A.43)A⋅A=|A|2=A2,
(1A.44)A⋅A​*=|A|2=A2,
(1A.45)A+B=B+A,
(1A.46)A⋅B=B⋅A,
(1A.47)A×B=−B×A,
(1A.48)(A+B)⋅C=A⋅C+B⋅C,
(1A.49)(A+B)×C=A×C+B×C,
(1A.50)A⋅B×C=B⋅C×A=C⋅A×B,
(1A.51)A×(B×C)=(A⋅C)B−(A⋅B)C,
(1A.52)(A×B)⋅(C×D)=A⋅B×(C×D)=A⋅(B⋅DC−B⋅CD)=(A⋅C)(B⋅D)−(A⋅D)(B⋅C),
(1A.53)(A×B)×(C×D)=(A×B⋅D)C−(A×B⋅C)D.

1A.3.2Differentiation

(1A.54)∇⋅(∇×A)=0,
(1A.55)∇×∇ψ=0,
(1A.56)∇(ϕ+ψ)=∇ϕ+∇ψ,
(1A.57)∇(ϕψ)=ϕ∇ψ+ψ∇ϕ,
(1A.58)∇⋅(A+B)=∇⋅A+∇⋅B,
(1A.59)∇×(A+B)=∇×A+∇×B,
(1A.60)∇⋅(ψA)=A⋅∇ψ+ψ∇⋅A,
(1A.61)∇×(ψA)=∇ψ×A+ψ∇×A,
(1A.62)∇(A⋅B)=(A⋅∇)B+(B⋅∇)A+A×(∇×B)+B×(∇×A),
(1A.63)∇⋅(A×B)=B⋅∇×A−A⋅∇×B,
(1A.64)∇×(A×B)=A∇⋅B−B∇⋅A+(B⋅∇)A−(A⋅∇)B,
(1A.65)∇×∇×A=∇(∇⋅A)−∇2A.

1A.3.3Integration

(1A.66)∮CA⋅dl=∬S(∇×A)ds(Stokes'theorem),
(1A.67)∯SA⋅ds=∭V(∇⋅A)dv(Divergencetheorem),
(1A.68)∯S(ˆn×A)ds=∭V(∇×A)dv,
(1A.69)∯Sψds=∭V∇ψdv,
(1A.70)∮Cψdl=∬Sˆn×∇ψds.

Reference

  1. 1.Balanis, C. A., Advanced Engineering Electromagnetics, Wiley, New York, 1989.
..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.
Reset
52.14.240.178