Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

Electromagnetics of Simple Media: One-Dimensional Solution*

2
Electromagnetics of Simple Media: One-Dimensional Solution *

The mathematics needed to solve problems may be simplified if we are able to model the problem as one-dimensional. Sometimes a practical problem with the appropriate symmetries and dimensions will permit us to use one-dimensional models. A choice of the appropriate coordinate system will sometimes allow us to reduce the dimensionality of the problem. A few of such basic solutions will be listed next.

2.1Uniform Plane Waves in Sourceless Medium (ρ_V = 0, J_source = 0)

A simple lossy medium with the parameters ε_r, μ_r, and σ has the following one-dimensional (say z-coordinate) solutions in Cartesian coordinates:

(2.1)

$E_{z} = H_{z} = 0,$

(2.2)

$η H = \hat{z} \times E,$

(2.3)

$E = E_{t} \{\begin{array}{c} e^{+ j k z} \\ e^{- j k z} \end{array}\} .$

In the above, the braces {} indicate a linear combination of the functions within parentheses and E_t is the electric field in the transverse (to z) plane. For a lossy medium,

(2.4)

$k^{2} = ω^{2} μ ε - j ω μ σ,$

and hence k is complex. The characteristic impedance η is given by

(2.5)

$η = {(\frac{j ω μ}{σ + j ω ε})}^{1 / 2},$

which is again complex. If k is written as (β − jα), then the phase factor exp(− jkz) = exp(−αz −jβz) gives the solution of an attenuated wave propagating in the positive z-direction. Here α is called the attenuation constant (Np/m) and β is called the phase constant (rad/m). Explicit expressions for α and β may be obtained by solving the two equations generated by equating the real and imaginary parts of the LHS with the RHS of Equation 2.4, respectively:

(2.6)

$α = ω \sqrt{μ ε} {\{\frac{1}{2} [\sqrt{1 + T^{2}} - 1]\}}^{1 / 2} (Np / m)$

(2.7)

$β = ω \sqrt{μ ε} {\{\frac{1}{2} [\sqrt{1 + T^{2}} + 1]\}}^{1 / 2} (rad /m)$

where

(2.8)

$T = \frac{σ}{ω ε}$

is called the loss tangent. For a low-loss dielectric, the loss tangent T ≪ 1 and

(2.9)

$α \approx \frac{σ}{2} \sqrt{\frac{μ}{ε}}, T ≪ 1,$

(2.10)

$β \approx ω \sqrt{μ ε}, T ≪ 1,$

(2.11)

$η \approx \sqrt{\frac{μ}{ε}} ∠ {tan}^{- 1} (\frac{σ}{2 ω ε}), T ≪ 1.$

2.2Good Conductor Approximation

For the other limit of approximation, called the good-conductor approximation,

(2.12)

$α \approx β \approx \sqrt{π f μ σ} = \frac{1}{δ}, T ≫ 1,$

(2.13)

$η \approx \frac{\sqrt{2}}{σ δ} ∠ 45 °, T ≫ 1.$

In the above, δ is called the skin depth. The characteristic impedance in this case is also called the surface impedance Z_s:

(2.14)

$η = Z_{s} = R_{s} + j X_{s} = (1 + j) \sqrt{\frac{ω μ}{2 σ}} .$

2.3Uniform Plane Wave in a Good Conductor: Skin Effect

The attenuated positive-going wave in a good conductor is described by the phasor exp [−(1 + j)z/δ] and the real fields are of the form

(2.15)

$E (z, t) = E_{0} e^{- z / δ} cos (ω t - \frac{z}{δ}),$

(2.16)

$J (z, t) = J_{0} e^{- z / δ} cos (ω t - \frac{z}{δ}),$

where

(2.17)

$J_{0} = σ E_{0} .$

From Equation 2.16, we see that the amplitude of the current density drops to e⁻¹ (36.8%) of its value at a distance

(2.18)

$δ = \frac{1}{\sqrt{π f μ σ}} .$

In the case of direct current (DC), f = 0 and δ = ∞, indicating that the current density can be uniform. However, for the time-harmonic AC case (f ≠ 0), δ is finite, indicating that the current density is nonuniform and decays exponentially with distance. For example, at a distance of 4δ, the current density reduces (e⁻⁴ = 1.8%) practically to zero. In Table 2.1, we list the skin depth δ for a good conductor such as copper at various frequencies.

TABLE 2.1
Skin Depth for Copper

f	60 Hz	1 kHz	1 MHz	10 GHz
δ	1 cm	2.45 mm	7.75 × 10⁻² mm	7.75 × 10⁻⁴ mm

At high frequencies, the current is practically confined to the skin of the conductor and the phenomenon is hence described as a skin effect.

2.4Boundary Conditions at the Interface of a Perfect Electric Conductor with a Dielectric

We also note that δ = 0 for σ = ∞. That is the reason for the statement in Problem P2.1 that the time-harmonic fields in a perfect conductor are zero. If medium 1 is a perfect conductor and medium 2 is a dielectric, then the boundary conditions are

(2.19)

${\hat{n}}_{12} \cdot D_{2} = ρ_{s},$

(2.20)

${\hat{n}}_{12} \cdot B_{2} = 0,$

(2.21)

${\hat{n}}_{12} \times E_{2} = 0,$

(2.22)

${\hat{n}}_{12} \times H_{2} = K .$

Thus, at the interface, the electric field is entirely normal to the interface and is equal to ρ_s/ε. Furthermore, the magnetic field is entirely tangential and is equal in magnitude to the surface current density K.

The PEC boundary condition

(2.23)

$E_{t} = 0$

implies

(2.24)

$\frac{\partial E_{n}}{\partial n} = 0,$

where $\hat{t}$ is a tangential unit vector and $\hat{n}$ is a normal unit vector. Also the PEC boundary condition

(2.25)

$H_{n} = 0$

implies

(2.26)

$\frac{\partial H_{t}}{\partial n} = 0.$

2.5AC Resistance

Figure 2.1 shows an infinitely deep good conductor of conductivity σ defined by the half-space 0 < x < ∞.

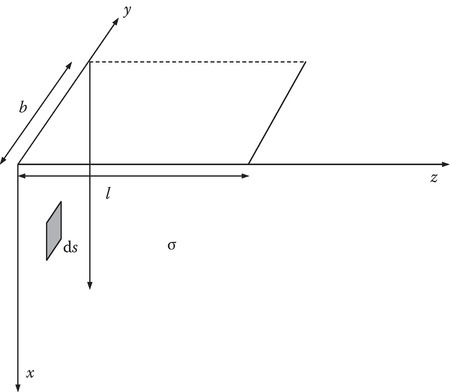
FIGURE 2.1
AC resistance of a semi-infinite good conductor.

The electric, magnetic, and current density phasors may be written as

(2.27)

$\tilde{E} (x) = \hat{z} E_{0} e^{- x / δ - j x / δ},$

(2.28)

$\tilde{H} (x) = - \hat{y} E_{0} \frac{σ δ}{\sqrt{2}} e^{- x / δ} e^{- j x / δ} e^{- j 45 °},$

and the corresponding real fields are

(2.29)

$E (x, t) = \hat{z} E_{0} e^{- x / δ} cos (ω t - \frac{x}{δ}) (V/m),$

(2.30)

$H (x, t) = - \hat{y} E_{0} \frac{σ δ}{\sqrt{2}} e^{- x / δ} cos (ω t - \frac{x}{δ} - 45 °) (A/m) .$

The time-averaged power density is given as

(2.31)

$〈S〉 = \hat{x} \frac{1}{2} E_{0}^{2} \frac{σ δ}{\sqrt{2}} e^{- 2 x / δ} cos 45 ° = \hat{x} \frac{1}{4} E_{0}^{2} σ δ e^{- 2 x / δ} .$

The total power entering the conductor of width b and length l is given by

(2.32)

$P = {〈S〉}_{x = 0} b l = \frac{1}{4} E_{0}^{2} σ δ b l .$

The total phasor current entering the conductor of width b is given by

(2.33)

$\tilde{I} = \iint \tilde{J} \cdot ds = \iint σ \tilde{E} \cdot ds = \int_{0}^{b} \int_{0}^{\infty} σ E_{0} e^{- (1 + j) x / δ} d x d y .$

After integrating and substituting the limits, we obtain

(2.34)

$\tilde{I} = \frac{σ E_{0} b δ}{\sqrt{2}} ∠ - 45 °,$

(2.35)

$I (t) = \frac{σ E_{0} b δ}{\sqrt{2}} cos (ω t - 45 °) .$

Let us define R_AC as an equivalent resistance that consumes the same power, that is,

(2.36)

${\tilde{I}}_{RMS}^{2} R_{AC} = Power consumed = P .$

From Equation 2.35, we obtain

(2.37)

${\tilde{I}}_{RMS} = \frac{σ E_{0} b δ}{2} .$

From Equations 2.35 and 2.33, we obtain

(2.38)

$R_{AC} = \frac{l}{σ b δ} .$

Note that if the current were uniformly distributed (DC case), then we would have got the same resistance as given by Equation 2.38 if the depth of the conductor was δ. Figure 2.2 shows this equivalence.

2.6AC Resistance of Round Wires

The AC resistance of a round wire of radius a and length l is easily calculated for the two extreme cases of approximation δ ≫ a and δ ≪ a. For the former, the current may be considered as uniformly distributed and the DC resistance formula may be used:

(2.39)

$R = \frac{l}{σ s} = \frac{l}{σ π a^{2}}, δ ≫ a .$

For the latter, the analysis of the previous section may be applied. The circular conductor may be considered as a semi-infinite solid because δ ≪ a. Therefore, the effective area of cross-section s_eff (Figure 2.3) is given by

(2.40)

$s_{eff} = π [a^{2} - {(a - δ)}^{2}] \approx 2 π a δ, δ ≪ a$

and

(2.41)

$R_{AC} = \frac{1}{2 π σ a δ}, δ ≪ a .$

The analysis is more involved for the case where δ is comparable to a. In this case, we have to take a fresh look at the solution based on the one-dimensional solution in cylindrical coordinates (see Appendix 2A).

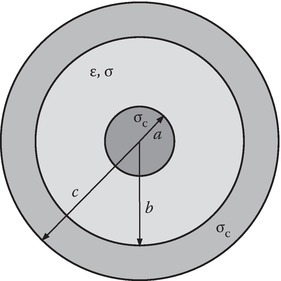
FIGURE 2.3
Cross section of a coaxial cable.

2.7Voltage and Current Harmonic Waves: Transmission Lines

A transmission line consists of two conductors that guide an electromagnetic wave from an electromagnetic source to an electromagnetic load. One approach to transmission line theory is through the distributed circuit theory. In this approach, we consider a differential length ∆z of a transmission line and describe its properties in terms of its per meter length circuit parameters, R′, the resistance due to imperfect conductors, L′, the inductance due to magnetic flux generated by the currents in the conductors, G′, the conductance due to an imperfect dielectric, and C′, the capacitance due to the surface charges on the conductors. We use electromagnetic theory to calculate the circuit parameters that depend on the electromagnetic properties of the materials used and their geometric arrangement. A parallel plate transmission line and a coaxial cable are two simple examples of transmission lines. Strip lines and microstrip lines are extensively used in high-frequency electromagnetic devices. Transmission line theory is often given in terms of voltage and current since in the transverse plane of a transmission line (cross section), the electromagnetic wave may be described as a TEM wave and the transverse fields satisfy the Laplace equation in the transverse plane. The voltage V and the current I can then be described as the appropriate integrals of the electric field and the magnetic field, respectively.

The parameters G′, L′, and C′ are computed as though the fields are static. For a coaxial cable (Figure 2.3), the parameters are given by [1]

(2.42)

$G^{'} = \frac{2 π σ}{ln (b / a)},$

(2.43)

$L^{'} = \frac{μ}{2 π} ln (\frac{b}{a}),$

(2.44)

$C^{'} = \frac{2 π ε}{ln (b / a)} .$

The formulas to be used for the calculation of R′ and the corrections to L′ due to the internal inductance of the conductor will depend on the frequency. The previous section discussed the calculation of these parameters at high frequencies.

For high frequencies, that is, δ ≪ a,

(2.45)

$R^{'} = [\frac{1}{2 π σ_{c} δ a} + \frac{1}{2 π σ_{c} δ b}],$

and L′ including the correction due to the internal inductance (inductance due to the magnetic flux in the conductors) is given by

(2.46)

$L^{'} = \frac{μ}{2 π} ln (\frac{b}{a}) + L^{″},$

where

(2.47)

$ω L^{″} = R^{'} .$

The parameters for other transmission lines may be calculated [1] using the same principles. After obtaining the parameters, the differential length transmission line may be represented as a two-port network shown in Figure 2.4 and expressed

(2.48)

$V (z, t) - V (z + Δ z, t) = R^{'} Δ z I (z, t) + L^{'} Δ z \frac{\partial I (z, t)}{\partial t},$

which, in the limit ∆z approaches zero reduces to

(2.49)

$- \frac{\partial V (z, t)}{\partial z} = R^{'} I (z, t) + L^{'} \frac{\partial I (z, t)}{\partial t} .$

Similar analysis for the current shows that

(2.50)

$I (z, t) - I (z + Δ z, t) = G^{'} Δ z V (z + Δ z, t) + C^{'} Δ z \frac{\partial V (z + Δ z, t)}{\partial t},$

which, in the limit ∆z approaches zero reduces to

(2.51)

$- \frac{\partial I (z, t)}{\partial z} = G^{'} V (z, t) + C^{'} \frac{\partial V (z, t)}{\partial t} .$

Equations 2.49 and 2.51 are the first-order coupled partial differential equations describing the voltage and current waves on a transmission line. The wave nature and the analogy with a simple electromagnetic wave may easily be seen by considering the following justifiable simplifications. As a first approximation, we can often neglect the losses in a transmission line and obtain the following wave equation for the voltage V(z, t):

(2.52)

$\frac{\partial^{2} V}{\partial z^{2}} - \frac{1}{v^{2}} \frac{\partial^{2} V}{\partial t^{2}} = 0, R^{'} = G^{'} = 0,$

where

(2.53)

$v = \frac{1}{\sqrt{L^{'} C^{'}}} .$

If the source is harmonic, then

(2.54)

$\frac{\partial^{2} \tilde{V}}{\partial z^{2}} + β^{2} \tilde{V} = 0,$

where

(2.55)

$β = \frac{ω}{v} .$

The solution may be written as

(2.56)

$\tilde{V} = {\tilde{V}}^{+} + {\tilde{V}}^{-},$

(2.57)

$\tilde{V} = {\tilde{V}}_{0}^{+} e^{- j β z} + {\tilde{V}}_{0}^{-} e^{+ j β z} .$

The superscript + is used for a positive-going wave and the superscript − is used for a negative-going wave. From Equation 2.49, the relationship between the voltages and the current may be obtained:

(2.58)

${\tilde{V}}^{+} = Z_{0} {\tilde{I}}^{+},$

(2.59)

${\tilde{V}}^{-} = - Z_{0} {\tilde{I}}^{-},$

where

(2.60)

$Z_{0} = \sqrt{\frac{L^{'}}{C^{'}}} .$

The following analogy with a TEM wave may be drawn:

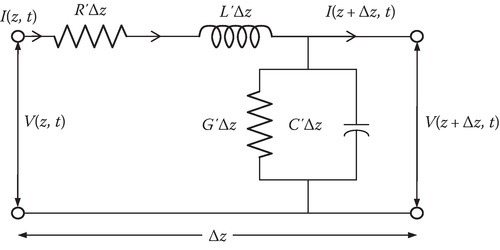
FIGURE 2.4
Circuit representation of a differential length of a transmission line.

Neglecting losses is equivalent to assumptions that the conductors are perfect (σ_c = ∞) and the dielectric is perfect (σ = 0). Practical lines have large but finite conductivity for conductors (e.g., copper σ_c = 5.7 × 10⁷ S/m) and small but nonzero conductivity for dielectrics (e.g., hard rubber, σ = 10⁻¹⁵ S/m). In such a case, R′ and G′ are nonzero and the propagation constant γ is

(2.61)

$γ = j k = \sqrt{(R^{'} + j ω L^{'}) (G^{'} + j ω C^{'})} = α + j β,$

and the characteristic impedance Z₀ is complex:

(2.62)

$Z_{0} = \sqrt{\frac{R^{'} + j ω L^{'}}{G^{'} + j ω C^{'}}} .$

As expected, the solution to the transmission line equation is a linear combination of positive-going and negative-going attenuated traveling waves. Also, from the field viewpoint, we realize that the electromagnetic wave is no longer a pure TEM wave. To drive the current through the conductors, which are not perfect, a small E_z-component is needed. The integral of this component along the length of the conductors gives the voltage drop. The cross product of this z-component with the magnetic field H gives the power density. The time-averaged power density integrated over the surface of the conductor gives the power consumed by the conductors. Problem P2.5 is constructed to illustrate the approximate method of solving a transmission line problem and to understand the power flow in a transmission line.

2.8Bounded Transmission Line

Figure 2.5 shows a transmission line of length d with a load at z = 0, and a source of voltage V_g and internal impedance Z_g connected at the point z = −d. From Equation 2.57 and Equation 2.58, the voltage at the terminals AB and the current ${\tilde{I}}_{g} = \tilde{I} (d)$ may be written as

(2.63)

$\tilde{V} (d) = {\tilde{V}}_{0}^{+} e^{j β d} + {\tilde{V}}_{0}^{-} e^{- j β d},$

(2.64)

$\tilde{I} (d) = \frac{1}{Z_{0}} [{\tilde{V}}_{0}^{+} e^{j β d} - {\tilde{V}}_{0}^{-} e^{- j β d}] .$

The input impedance is given by

(2.65)

$Z (d) = \frac{\tilde{V} (d)}{\tilde{I} (d)} = Z_{0} [\frac{1 + Γ_{0} e^{- j 2 β d}}{1 - Γ_{0} e^{- j 2 β d}}],$

where Γ₀ is the reflection coefficient at the load and is given by

(2.66)

$Γ_{0} = \frac{{\tilde{V}}_{0}^{-}}{{\tilde{V}}_{0}^{+}} = \frac{Z_{L} - Z_{0}}{Z_{L} + Z_{0}} .$

By substituting Equation 2.66 into Equation 2.65, the input impedance may be written in an alternative form as

(2.67)

$Z (d) = Z_{0} \frac{Z_{L} cos β d + j Z_{0} sin β d}{Z_{0} cos β d + j Z_{L} sin β d} .$

From Equation 2.67, several formulas for special lengths may be obtained

(2.68)

$Z (\frac{λ}{4}) = \frac{Z_{0}^{2}}{Z_{L}},$

(2.69)

$Z (\frac{λ}{2}) = Z_{L} .$

The circuit approximation applies if $d ≪ λ = \frac{2 π}{β} :$

(2.70)

$Z (d) = Z_{L}, \frac{d}{λ} ≪ 1.$

For a matched line, that is, Z_L = Z₀, Γ₀ = 0, and

(2.71)

$Z (d) = Z_{L} if Z_{L} = Z_{0} .$

Equation 2.71 shows that for the matched line the length of the line has no effect on the input impedance, the right-going wave travels from the source to the load, there is no reflected wave, and the source wave is absorbed by the load. See Appendix 2B for power calculations.

A graphical method based on “Smith chart” is available to calculate the input impedance [1]. Appendix 2C gives the theory and application of the Smith chart.

The input impedance is reactive, if the load is either short-circuited or open-circuited and the reflection coefficient has a magnitude of 1:

(2.72)

$Z (d) = j Z_{0} tan β d, Z_{L} = 0,$

(2.73)

$Z (d) = - j Z_{0} cot β d, Z_{L} = \infty .$

In the above two cases, the waves are standing waves, there are permanent nulls in voltage at certain points on the transmission line, and the source does not supply any real power to the load but supplies only a reactive power.

Transmission line serves as a powerful analog for describing many electromagnetic phenomena since voltage and current variables are easily measurable and electrical engineers have a certain feel for these variables. Appendix 2B may be consulted for details of the transmission line theory. See Appendix 2C for application of the Smith chart to wave reflection problems.

The theory and applications of nonuniform transmission lines is given in Appendix 2D.

2.9Electromagnetic Wave Polarization

A plane wave solution given by Equation 2.1, Equation 2.2 and Equation 2.3 allows for x- and y-components of the electric and magnetic fields. Let

(2.74)

${\tilde{E}}_{t} (z) = \tilde{E} (z) = \hat{x} {\tilde{E}}_{x} (z) + \hat{y} {\tilde{E}}_{y} (z) .$

Furthermore, let

(2.75)

${\tilde{E}}_{x} (z) = E_{x 0} e^{- j k z},$

(2.76)

${\tilde{E}}_{y} (z) = E_{y 0} e^{j δ} e^{- j k z},$

where E_x0, E_y0, and δ are real numbers. The instantaneous vector electric field is given by

(2.77)

$E (z, t) = \hat{x} E_{x 0} cos (ω t - k z) + \hat{y} E_{y 0} cos (ω t - k z + δ) .$

A wave is said to be linearly polarized if δ = 0 or π. This is because, at a specified value of z, say z = 0, the tip of E(0, t) traces a straight line in the x−y-plane. For δ = 0,

(2.78)

$E (0, t) = (\hat{x} E_{x 0} + \hat{y} E_{y 0}) cos ω t .$

Figure 2.6a depicts this case. If, furthermore, E_y0 = 0, the wave is said to be x-polarized. On the other hand, if E_x0 = 0, the wave is said to be y-polarized. A wave is said to have left-hand circular polarization (LHC polarization) or L wave as it is called in this book, if δ = π/2 and E_x0 = E_y0 = E₀, that is,

(2.79)

$E (z, t) = \hat{x} E_{0} cos (ω t - k z) + \hat{y} E_{0} cos (ω t - k z + π / 2),$

or as a vector phasor

(2.80)

$\tilde{E} (z) = (\hat{x} + j \hat{y}) E_{0} e^{- j k z} (L wave) .$

Figure 2.6b shows E(0,t) for various values of ωt. The tip of the E vector traces a circle. If the thumb of the left hand is pointed in the direction of wave propagation, the other four fingers point in the direction of the rotation of E.

FIGURE 2.6
(a) Linearly polarized wave (δ = 0). (b) L wave. (c) R wave. (d) Elliptic polarization.

A wave is said to have a right-hand circular polarization, if δ = − π/2 and E_x0 = E_y0 = E₀, that is,

(2.81)

$E (z, t) = \hat{x} E_{0} cos (ω t - k z) + \hat{y} E_{0} cos (ω t - k z - π / 2),$

or as a vector phasor

(2.82)

$\tilde{E} (z) = (\hat{x} - j \hat{y}) E_{0} e^{- j k z} (R wave) .$

Figure 2.6c shows E(0, t) for various values of E. The tip of the E vector traces a circle. If the thumb of the right hand points in the direction of propagation, the other four fingers point in the direction of rotation of E.

A wave is said to be elliptically polarized if none of the conditions stated above is satisfied. In this most general case, the tip of E traces an ellipse in the x–y-plane. The shape of the ellipse and its handedness are determined by the values of E_y0/E_x0 and the polarization phase difference δ. Figure 2.6d shows a wave with elliptic polarization. An elliptically polarized wave may be shown to be a linear combination of L and R waves. A linearly polarized wave is a different linear combination of L and R waves.

2.10Arbitrary Direction of Propagation

Figure 2.7 shows a uniform plane wave propagating at an angle θ in the x−z-plane. The wave is still a one-dimensional wave propagating in the direction of ζ-coordinate, which can be expressed in terms of x and z:

(2.83)

$ζ = x sin θ + z cos θ .$

The exponential factor is given by

(2.84)

$e^{- j k ς} = e^{- j k (S x + C z)},$

where

(2.85)

$S = sin θ, C = cos θ .$

We can have two cases of TEM waves, one with the electric field in the plane of incidence and the other with the electric field normal to the plane of incidence. The former is called a p wave and the latter an s wave. The p wave has the magnetic field perpendicular to the plane of incidence. If the z-axis is normal to an interface (boundary), then one can define wave impedance Z_w as the ratio of the tangential components of the electric and magnetic fields. For the geometry shown in Figure 2.9, we have

(2.86)

$Z_{w} = \frac{|E_{x}|}{|H_{y}|} = \frac{E cos θ}{H} = η cos θ .$

Similarly, for an s wave (Figure 2.10),

(2.87)

$Z_{w} = \frac{|E_{y}|}{|H_{x}|} = \frac{E}{H cos θ} = \frac{η}{cos θ} .$

The p wave is also referred to as a parallel-polarized wave and the s wave as a perpendicular-polarized wave.

FIGURE 2.7
Arbitrary direction of propagation.

2.11Wave Reflection

At an interface between two media, the wave energy, in general, is partly transmitted and partly reflected. At an interface with a perfect conductor, the wave is totally reflected. The boundary condition E_t = 0 at a PEC suggests an analogy with a short-circuited transmission line (Figure 2.8).

Instead of an interface with a PEC, if we have a boundary with a good conductor, then we should use for the load impedance Z_L = Z_s, where Z_s is given by Equation 2.14.

2.12Incidence of p Wave: Parallel-Polarized

Figure 2.9 shows a p wave propagating obliquely in the x–z-plane. The transmission line analogy is also shown. The problem may be solved as an electromagnetic boundary value problem. The unknowns may be reduced to $E_{x}^{R}$ and $E_{x}^{T}$ , the tangential components of the reflected wave R and the transmitted wave T, respectively. All the other components in either medium may be expressed in terms of these two unknowns and $E_{x}^{I}$ , where the superscript I indicates an incident wave. The unknowns may be determined from the boundary conditions on tangential components of E and H at z = 0 for all t and x:

(2.88)

$E_{x 1} = E_{x}^{I} + E_{x}^{R} = E_{x 2} = E_{x}^{T},$

(2.89)

$H_{y_{1}} = H_{y}^{I} + H_{y}^{R} = H_{y 2} = H_{y}^{T} .$

The satisfaction of the condition for all t imposes the requirement that the frequency of all the waves is same, and the satisfaction of the conditions, for all x, imposes the Snell’s law:

(2.90)

$ω_{1} = ω_{R} = ω_{T},$

(2.91)

$k_{1} sin θ_{1} = k_{R} sin θ_{R} = k_{2} sin θ_{2} .$

Sections 9.2 and 9.4 discuss these points in more detail. The solution of the boundary value problem may be completed by imposing Equations 2.88 and 2.89 subject to Equations 2.90 and 2.91. Alternatively, we can use the transmission line analogy given in Figure 2.9 and can also use Equation 2.66 for obtaining the reflection and transmission coefficients Γ₀ and T₀, respectively:

(2.92)

$Γ_{0} = \frac{V_{0}^{-}}{V_{0}^{+}} = \frac{Z_{L} - Z_{0}}{Z_{L} + Z_{0}} = \frac{η_{2} cos θ_{2} - η_{1} cos θ_{1}}{η_{2} cos θ_{2} + η_{1} cos θ_{1}} = \frac{E_{xp}^{R}}{E_{xp}^{I}} = Γ_{p 1},$

(2.93)

$T_{0} = \frac{V_{0}}{V_{0}^{+}} = 1 + Γ = \frac{2 Z_{L}}{Z_{L} + Z_{0}} = \frac{2 η_{2} cos θ_{2}}{η_{2} cos θ_{2} + η_{1} cos θ_{1}} = \frac{E_{xp}^{T}}{E_{xp}^{I}} = T_{p 1} .$

It follows immediately that the reflection coefficient is zero if

(2.94)

$η_{2} cos θ_{2} = η_{1} cos θ_{1} .$

Further simplification of Equation 2.94 results if θ₁ and θ₂ are related through Snell’s law (Equation 2.91). The angle θ₁ = θ_Bp for which Equation 2.94 is satisfied is called the Brewster angle and is given by

(2.95)

$θ_{Bp} = {tan}^{- 1} \sqrt{\frac{ε_{2}}{ε_{1}}} .$

A similar analysis for the s wave shows that θ_Bs does not exist for nonmagnetic materials. For the p wave, sometimes, the reflection and transmission coefficients are defined in terms of the ratios of the magnitude of the entire electric fields rather than the tangential components:

(2.96)

$T_{p} = \frac{E_{p}^{T}}{E_{p}^{I}} = \frac{E_{xp}^{T} / cos θ_{2}}{E_{xp}^{I} / cos θ_{1}} = \frac{cos θ_{1}}{cos θ_{2}} T_{p 1} .$

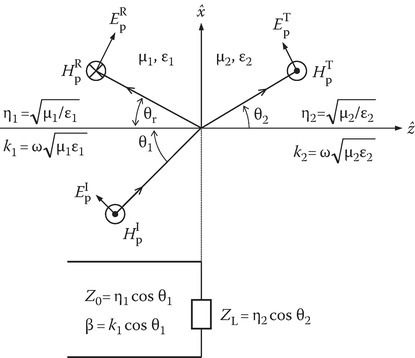
FIGURE 2.9
Oblique incidence of a p wave on a dielectric–dielectric interface. Transmission line analogy.

2.13Incidence of s Wave: Perpendicular-Polarized

Figure 2.10 shows an s wave propagating obliquely in x–z-plane. The transmission line analogy is also shown. Equations 2.90 and 2.91 still hold for the reasons mentioned before. The boundary conditions in this case can be stated as, at z = 0, for all t and x:

(2.97)

$E_{y 1} = E_{y}^{I} + E_{y}^{R} = E_{y 2} = E_{y}^{T},$

(2.98)

$H_{x 1} = H_{x}^{I} + H_{x}^{R} = H_{x 2} = H_{x}^{T} .$

From the transmission line analogy shown in Figure 2.10 and Equation 2.66, the reflection and transmission coefficients are given respectively, by,

(2.99)

$Γ_{s} = \frac{E_{y}^{R}}{E_{y}^{I}} = = \frac{η_{2} / cos θ_{2} - η_{1} / cos θ_{1}}{η_{2} / cos θ_{2} + η_{1} / cos θ_{1}},$

(2.100)

$T_{s} = \frac{E_{y}^{T}}{E_{y}^{I}} = \frac{2 η_{2} / \cos θ_{2}}{η_{2} / \cos θ_{2} + η_{1} / \cos θ_{1}} .$

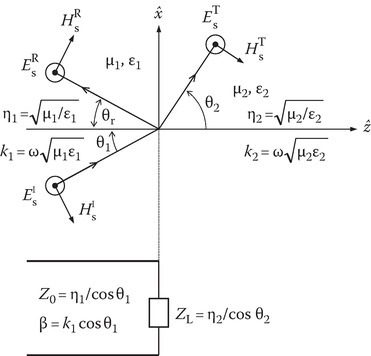
FIGURE 2.10
Oblique incidence of an s wave on a dielectric–dielectric interface. Transmission line analogy.

2.14Critical Angle and Surface Wave

Let us next consider wave propagation from an optically dense medium to an “optically rare” medium. In optics, a nonmagnetic medium is described in terms of the refractive index n, which is related to the dielectric constant through

(2.101)

$n = \sqrt{ε_{r}} .$

The problem under consideration assumes that ε₁ > ε₂ or n₁ > n₂. From Snell’s law (Equation 2.91),

(2.102)

$\frac{sin θ_{2}}{sin θ_{1}} = \frac{k_{1}}{k_{2}} = \sqrt{\frac{ε_{1}}{ε_{2}}} = \frac{n_{1}}{n_{2}} > 1.$

Note that θ₂ > θ₁ if n₁ > n₂. The angle of transmission θ₂ = 90° when

(2.103)

$θ_{1} = θ_{c} = {sin}^{- 1} \frac{n_{2}}{n_{1}}, θ_{2} = 90 ° .$

Such an angle of incidence θ_c is called a critical angle. For this angle, the wave no longer propagates into medium 2 and in fact it propagates along the interface. However, we still have a reflected wave, with the angle of reflection θ_r = θ_c. The wave is said to be totally reflected since there is no power flow into medium 2. Since θ₂ = 90°, the second medium for p wave propagation behaves like a short-circuited load and for s wave propagation as an open-circuited load. The magnitude of the reflection coefficient in either case is 1. The wave is totally reflected. Let us examine further what happens at the critical angle by considering s wave propagation. The reflection coefficient Γ_s = 1 and the transmission coefficient T_s = 2. Furthermore,

(2.104)

$E_{s}^{T} = \hat{y} 2 E_{s}^{I} e^{- j k_{2} x},$

(2.105)

$H_{s}^{T} = \hat{z} \frac{2 E_{s}^{I}}{η_{2}} e^{- j k_{2} x},$

which represent a plane wave that travels along the interface in the positive x-direction. The time-averaged power densities of various waves are given by

(2.106)

$〈S^{T}〉 = \hat{x} \frac{2 {|E_{s}^{I}|}^{2}}{η_{2}},$

(2.107)

$〈S^{R}〉 = \frac{2 {|E_{s}^{I}|}^{2}}{2 η_{1}} [\hat{x} sin θ_{1} - \hat{z} cos θ_{1}],$

(2.108)

$〈 S^{I} 〉 = \frac{2 {| E_{s}^{I} |}^{2}}{2 η_{1}} [\hat{x} \sin θ_{1} + \hat{z} \cos θ_{1}] .$

Figure 2.11 shows the constant phase planes in medium 2.

FIGURE 2.11
Constant phase planes in medium 2 for θ₁ = θ_c.

When the angle of incidence θ₁ > θ_c, then

(2.109)

$sin θ_{2} = \frac{k_{1}}{k_{2}} sin θ_{1} = \frac{n_{1}}{n_{2}} sin θ_{1} > 1.$

The equation can be satisfied only if θ₂ is complex [2]:

(2.110)

$θ_{2} = θ_{R} + j θ_{X}, θ_{1} > θ_{c} .$

The transmitted electric field may be written as

(2.111)

$E_{s}^{T} (z) = \hat{y} T_{s} E_{s}^{I} e^{- α_{e} z} e^{- j β_{e} x},$

where

(2.112)

$α_{e} = k_{2} \sqrt{\frac{n_{1}^{2}}{n_{2}^{2}} \sin^{2} θ_{1} - 1}, θ_{1} > θ_{c},$

(2.113)

$β_{e} = k_{2} \frac{n_{1}}{n_{2}} sin θ_{1}, θ_{1} > θ_{c},$

and the phase velocity of this wave is given by

(2.114)

$v_{Pe} = \frac{ω}{β_{e}} = \frac{v_{P 2}}{(\frac{n_{1}}{n_{2}}) sin θ_{1}} < v_{P 2} = \frac{ω}{k_{2}} .$

This wave is a surface wave. The wave propagates in the positive x-direction but attenuates in the positive z-direction. Figure 2.12 shows the constant-amplitude planes (dotted lines) and the constant-phase planes (solid lines). The wave, while traveling along the interface with phase velocity v_Pe less than the phase velocity of an ordinary wave in the second medium v_P2, rapidly decays in the z-direction. Such a wave is labeled as a tightly bound slow surface wave. The imaginary part of the complex Poynting vector 〈S_I〉 = (1/2) Im[E × H*] represents the time-averaged reactive power density. For θ₁ > θ_c, it may be shown that [3]

(2.115)

$〈 S_{I} 〉 = \frac{1}{2} \hat{z} \sqrt{{(\frac{n_{1}}{n_{2}} \sin θ_{1})}^{2} - 1} \frac{{| T_{s} |}^{2} {| E_{s}^{I} |}^{2}}{η_{2}} e^{- 2 α_{e} z}, θ_{1} > θ_{c} .$

The wave penetrates the medium to a depth of 1/α_e and the energy in the second medium is a stored energy. The wave in the second medium is called an evanescent wave. The attenuation of the evanescent wave is different from the attenuation of a traveling wave in a conducting medium. The former indicates the localization of wave energy near the interface. Because of this penetration, it may be shown that an optical beam of finite cross section will be displaced laterally relative to the incident beam at the boundary surface. This shift is known as the Goos–Hanschen shift and is discussed in [3].

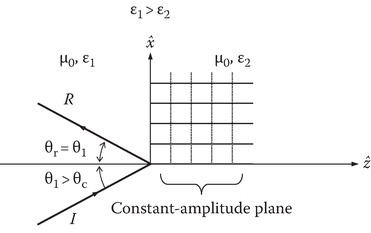
FIGURE 2.12
Constant-phase planes and constant-amplitude planes, for θ₁ > θ_c.

We will come across the evanescent wave in several other situations. The wave in a waveguide whose frequency is less than that of the cutoff frequency of the wave is an evanescent wave. The wave in a plasma medium, whose frequency is below “plasma frequency,” is an evanescent wave. The wave in the cladding of an optical fiber is an evanescent wave. Section 9.5 discusses the tunneling of power through a plasma slab by evanescent waves.

2.15One-Dimensional Cylindrical Wave and Bessel Functions

Let an infinitely long wire in free space be along the z-axis carrying a time harmonic current ${\tilde{I}}_{0}$ . From Equation 1.50, it is clear that the vector potential A will have only the z-component and from the symmetry it is also clear that the component is at the most a function of the cylindrical radial coordinate ρ:

(2.116)

$\tilde{A} = \hat{z} A (ρ) .$

From Equation 1.47 we get

(2.117)

$\nabla^{2} A + k_{0}^{2} A = 0, ρ > 0,$

(2.118)

$k_{0} = ω \sqrt{μ_{0} ε_{0}} = \frac{ω}{c} .$

Since A is a function of ρ only, Equation 2.117 becomes an ordinary differential equation of the form

(2.119)

$\frac{d^{2} A}{d ρ^{2}} + \frac{1}{ρ} \frac{d A}{d ρ} + k_{0}^{2} A = 0,$

which is the Bessel equation. It has two independent solutions J₀ and Y₀. These are analogous to cosine and sine functions that are the independent solutions for the Cartesian case. Linear combinations of J₀ and Y₀ give other functions to represent traveling waves in cylindrical coordinates. Table 2.2 gives the power series [4] for these functions and also differential and integral relations involving these functions. Table 2.3 lists these functions and also gives analogous functions in Cartesian coordinates. Since we are on the topic of Bessel functions, J_m and Y_m are the solutions of a more general Bessel equation

(2.120)

$\frac{d^{2} f}{d ρ^{2}} + \frac{1}{ρ} \frac{d f}{d ρ} + [k_{0}^{2} - \frac{m^{2}}{ρ^{2}}] f = 0.$

The sketches of the functions J_m and Y_m for various values of m and real values of the argument are given in Figure 2.13.

TABLE 2.2
Bessel Functions: Definitions and Relations

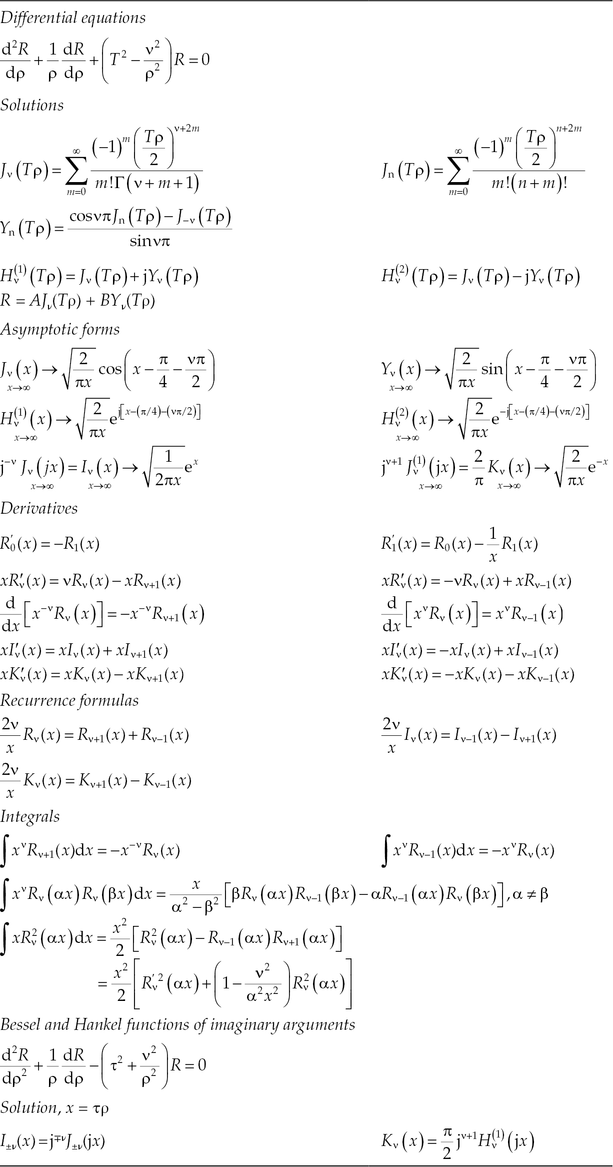
TABLE 2.3
Wave Functions in Cylindrical and Cartesian Coordinates

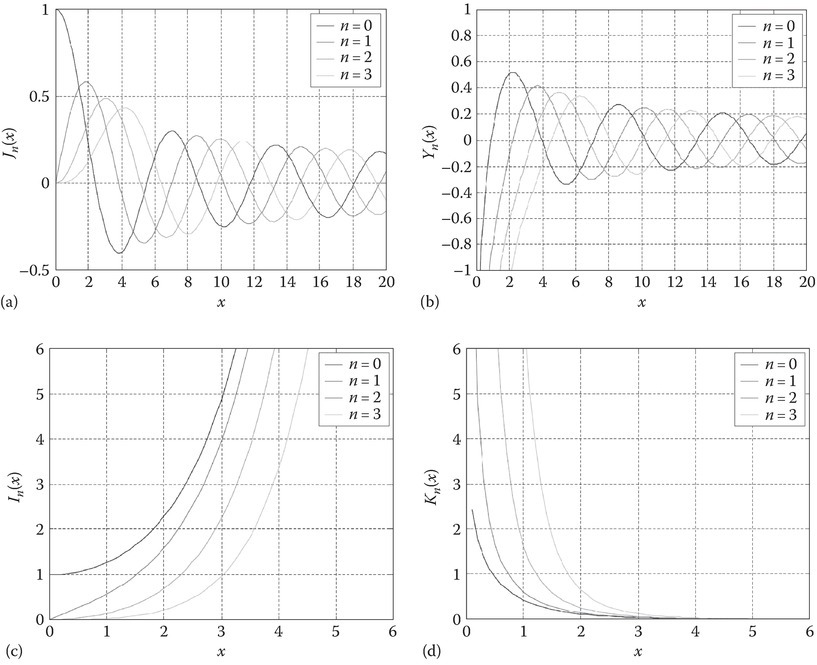
FIGURE 2.13
(a) Bessel functions of the first kind. (b) Bessel functions of the second kind. (c) Modified Bessel functions of the first kind. (d) Modified Bessel functions of the second kind.

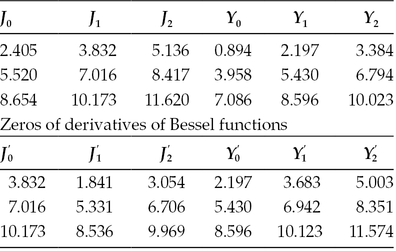
Table 2.4 lists the zeros χ _mn of the Bessel function J_m and the zeros $χ_{m n}^{'}$ of the derivative of the Bessel function $J_{m}^{'}$ with respect to its argument. The second subscript n denotes the nth zero of these oscillatory functions. These higher-order Bessel functions will be used in solving the cylindrical waveguide problems.

Getting back to the subject of the electromagnetic fields due to harmonic current ${\tilde{I}}_{0}$ in an infinitely long wire, the solution of Equation 2.119 that fits the requirement of an outgoing wave as k₀ρ tends to infinity is expressed in terms of a Hankel function of the second kind (see Table 2.2):

(2.121)

$\tilde{A} (ρ) = A_{0} H_{0}^{(2)} (k_{0} ρ),$

where A₀ is a constant to be determined. All the components of the electric and magnetic fields may be obtained from Maxwell’s equations and Equation 2.121:

(2.122)

${\tilde{H}}_{ϕ} = - \frac{1}{μ} \frac{\partial A}{\partial ρ} = - k_{0} \frac{A_{0}}{μ} {H^{'}}_{0}^{(2)} (k_{0} ρ),$

(2.123)

${\tilde{H}}_{ρ} = {\tilde{H}}_{z} = 0,$

(2.124)

${\tilde{E}}_{ρ} = {\tilde{E}}_{ϕ} = 0,$

(2.125)

${\tilde{E}}_{z} = - j ω A_{0} H_{0}^{(2)} (k_{0} ρ) .$

Application of Ampere’s law for a circular contour C in the x–y-plane of radius ρ, in the limit ρ → 0, relates the constant A₀ to the current ${\tilde{I}}_{0}$ :

(2.126)

$A_{0} = - j \frac{μ_{0}}{4} {\tilde{I}}_{0} .$

In obtaining Equation 2.126, the following small-argument approximation is used:

(2.127)

$lim_{k_{0} ρ \to 0} H_{1}^{(2)} (k_{0} ρ) = j \frac{2}{π} \frac{1}{k_{0} ρ} .$

The fields ${\tilde{E}}_{z}$ and ${\tilde{H}}_{ϕ}$ are given by

(2.128)

${\tilde{E}}_{z} = - \frac{k_{0} η_{0}}{4} {\tilde{I}}_{0} H_{0}^{(2)} (k_{0} ρ),$

(2.129)

${\tilde{H}}_{ϕ} = - j \frac{k_{0}}{4} {\tilde{I}}_{0} H_{1}^{(2)} (k_{0} ρ) .$

Equations 2.128 and 2.129 are the fields of a one-dimensional cylindrical wave. It can be shown that the wave impedance in the far-zone is

(2.130)

$Z_{w} = lim_{k_{0} ρ \to \infty} \frac{{\tilde{E}}_{z}}{- {\tilde{H}}_{ϕ}} = η_{0} .$

Since the wave impedance is equal to the intrinsic impedance of the medium, the wave is a TEM as shown in Figure 2.14.

FIGURE 2.14
One-dimensional cylindrical wave.

References

1.Ulaby, F.T., Applied Electromagnetics, Prentice Hall, Englewood Cliffs, NJ, 1999.
2.Balanis, C.A., Advanced Engineering Electromagnetics, Wiley, New York, 1989.
3.Lekner, J., Theory of Reflection, Kluwer Academic Publishers, Boston, MA, 1987.
4.Ramo, S., Whinnery, J.R., and Van Duzer, T.V., Fields and Waves in Communication Electronics, 3rd edition, Wiley, New York, 1994.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for 2. Electromagnetics of Simple Media: One-Dimensional Solution

Create new playlist

Sign In

Sign Up

Table of Contents for
2. Electromagnetics of Simple Media: One-Dimensional Solution