Reduction of dimensionality is often necessary in the analysis of complex multivariate datasets, which is always in high-dimensional format. So, for example, problems modeled by the number of variables present, the data mining tasks on the multidimensional analysis of qualitative data. There are also many methods for data dimension reduction for qualitative data.
The goal of dimensionality reduction is to replace large matrix by two or more other matrices whose sizes are much smaller than the original, but from which the original can be approximately reconstructed, usually by taking their product with loss of minor information.
An eigenvector for a matrix is defined as when the matrix (A in the following equation) is multiplied by the eigenvector (v in the following equation). The result is a constant multiple of the eigenvector. That constant is the eigenvalue associated with this eigenvector. A matrix may have several eigenvectors.
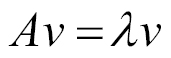
An eigenpair is the eigenvector and its eigenvalue, that is, (
) in the preceding equation.
The Principal-Component Analysis (PCA) technique for dimensionality reduction views data that consists of a collection of points in a multidimensional space as a matrix, in which rows correspond to the points and columns to the dimensions.
The product of this matrix and its transpose has eigenpairs, and the principal eigenvector can be viewed as the direction in the space along which the points best line up. The second eigenvector represents the direction in which deviations from the principal eigenvector are the greatest.
Dimensionality reduction by PCA is to approximate the data by minimizing the root-mean-square error for the given number of columns in the representing matrix, by representing the matrix of points by a small number of its eigenvectors.
The singular-value decomposition (SVD) of a matrix consists of following three matrices:
- U
- ∑
- V
U and V are column-orthonormal; as vectors, the columns are orthogonal and their length is 1. ∑ is a diagonal matrix and the values along its diagonal are called singular values. The original matrix equals to the product of U, ∑, and the transpose of V.
SVD is useful when there are a small number of concepts that connect the rows and columns of the original matrix.
Dimensionality reduction by SVD for matrix U and V are typically as large as the original. To use fewer columns for U and V, delete the columns corresponding to the smallest singular values from U, V, and ∑. This minimizes the error in reconstruction of the original matrix from the modified U, ∑, and V.
The CUR decomposition seeks to decompose a sparse matrix into sparse, smaller matrices whose product approximates the original matrix.
The CUR chooses from a given sparse matrix a set of columns C and a set of rows R, which play the role of U and 
in SVD. The choice of rows and columns is made randomly with a distribution that depends on the square root of the sum of the squares of the elements. Between C and R is a square matrix called U, which is constructed by a pseudo-inverse of the intersection of the chosen rows and columns.