Appendix 1D: Low-Frequency Approximation of Maxwell’s Equations R, L, C, and Memristor M

Search in book...
Toggle Font Controls
Create new playlist

Name your new playlist

Playlist description (optional)
Sign In

Email address

Password

Forgot Password?

or

Continue with Facebook

Continue with Google
Sign Up

Full Name

Email address

Confirm Email Address

Password

or

Continue with Facebook

Continue with Google

1D.1Introduction

Circuit theory, used extensively in low-frequency electrical engineering, is a low-frequency approximation of Maxwell’s equations. It is formulated in terms of the two-terminal circuit elements such as resistance (R), inductance (L), and capacitance (C). Fano et al. [1] discussed circuit theory as a quasistatic approximation in terms of the time-rate parameter α, which was used to expand the electromagnetic fields in power series. The classical elements R, L, and C were shown to be obtained by certain combinations of the zeroth- and first-order solutions. Chua [2] pointed out that a new circuit element M, called memristor (memory + resistor), could be proposed based on the relationship between the charge q(t) and the magnetic flux Φ_m(t). Such a two-terminal element realized recently [3] has interesting properties and applications.

1D.2Time-Rate Parameter

In preparing for generating quasistatic solutions, let us first consider the family of solutions generated by changing the timescale of the excitation. As an example, suppose the excitation is ρ(x, y, z, t), consider the family of solutions obtained by the excitation ρ(x, y, z, αt), where α is called the time-rate parameter. We can rewrite Maxwell’s equations in terms of the variable

(1D.1)

τ = α t .

$τ = α t .$

Then

(1D.2)

\frac{\partial \bar{B}}{\partial t} = \frac{\partial \bar{B}}{\partial τ} \frac{\partial τ}{\partial t} = α \frac{\partial \bar{B}}{\partial τ} .

$\frac{\partial \bar{B}}{\partial t} = \frac{\partial \bar{B}}{\partial τ} \frac{\partial τ}{\partial t} = α \frac{\partial \bar{B}}{\partial τ} .$

Maxwell’s equations (1.1), equations (1.2), equations (1.3) and equations (1.5) can now be written as

(1D.3)

\bar{\nabla} \times \bar{E} (\bar{r}, τ) = - α \frac{\partial \bar{B}}{\partial τ} (\bar{r}, τ),

$\bar{\nabla} \times \bar{E} (\bar{r}, τ) = - α \frac{\partial \bar{B}}{\partial τ} (\bar{r}, τ),$

(1D.4)

\bar{\nabla} \times \bar{H} (\bar{r}, τ) = \bar{J} + α \frac{\partial \bar{D}}{\partial τ} (\bar{r}, τ),

$\bar{\nabla} \times \bar{H} (\bar{r}, τ) = \bar{J} + α \frac{\partial \bar{D}}{\partial τ} (\bar{r}, τ),$

(1D.5)

\bar{\nabla} \cdot \bar{D} (\bar{r}, τ) = ρ_{v} (\bar{r}, τ),

$\bar{\nabla} \cdot \bar{D} (\bar{r}, τ) = ρ_{v} (\bar{r}, τ),$

(1D.6)

\bar{\nabla} \cdot \bar{B} (\bar{r}, τ) = 0,

$\bar{\nabla} \cdot \bar{B} (\bar{r}, τ) = 0,$

and Equation 1.5 becomes

(1D.7)

\bar{\nabla} \cdot \bar{J} (\bar{r}, τ) = - α \frac{\partial ρ_{v}}{\partial τ} (\bar{r}, τ) .

$\bar{\nabla} \cdot \bar{J} (\bar{r}, τ) = - α \frac{\partial ρ_{v}}{\partial τ} (\bar{r}, τ) .$

Since the fields are functions of $\bar{r}, τ$ $\bar{r}, τ$ , and the parameter α, they can be expressed in power series in terms of α as

(1D.8a)

\bar{E} (\bar{r}, τ, α) = {\bar{E}}_{0} (\bar{r}, τ) + α {\bar{E}}_{1} (\bar{r}, τ) + α^{2} {\bar{E}}_{2} (\bar{r}, τ) + \dots,

$\bar{E} (\bar{r}, τ, α) = {\bar{E}}_{0} (\bar{r}, τ) + α {\bar{E}}_{1} (\bar{r}, τ) + α^{2} {\bar{E}}_{2} (\bar{r}, τ) + \dots,$

where

(1D.8b)

{\bar{E}}_{k} (\bar{r}, τ) = \frac{1}{k!} {[\frac{\partial^{k} \bar{E} (\bar{r}, τ, α)}{\partial α^{k}}]}_{α = 0}, k = 1, 2, \dots,

${\bar{E}}_{k} (\bar{r}, τ) = \frac{1}{k!} {[\frac{\partial^{k} \bar{E} (\bar{r}, τ, α)}{\partial α^{k}}]}_{α = 0}, k = 1, 2, \dots,$

\bar{\nabla} \times \bar{E} = \bar{\nabla} \times {\bar{E}}_{0} + α \bar{\nabla} \times {\bar{E}}_{1} + α^{2} \bar{\nabla} \times {\bar{E}}_{2} + \dots .

$\bar{\nabla} \times \bar{E} = \bar{\nabla} \times {\bar{E}}_{0} + α \bar{\nabla} \times {\bar{E}}_{1} + α^{2} \bar{\nabla} \times {\bar{E}}_{2} + \dots .$

If we use similar power-series expressions and use in Equation 1D.3, Equation 1D.4, Equation 1D.5, Equation 1D.6 and Equation 1D.7 and collect terms to the same power of α, for instance, then we obtain

(1D.9)

\bar{\nabla} \times {\bar{E}}_{0} + α (\bar{\nabla} \times {\bar{E}}_{1} + \frac{\partial {\bar{B}}_{0}}{\partial τ}) + α^{2} (\bar{\nabla} \times {\bar{E}}_{2} + \frac{\partial {\bar{B}}_{1}}{\partial τ}) + \dots = 0.

$\bar{\nabla} \times {\bar{E}}_{0} + α (\bar{\nabla} \times {\bar{E}}_{1} + \frac{\partial {\bar{B}}_{0}}{\partial τ}) + α^{2} (\bar{\nabla} \times {\bar{E}}_{2} + \frac{\partial {\bar{B}}_{1}}{\partial τ}) + \dots = 0.$

Similar equations can be obtained, based on Equation 1D.4, Equation 1D.5, Equation 1D.6, Equation 1D.7, Equation 1D.8 and Equation 1D.9.

Equation 1D.9 must be satisfied, for all values of α. This can be met only if the coefficients of all the powers of α are separately equal to zero. Thus, we obtain the series of equations

(1D.10)

\bar{\nabla} \times {\bar{E}}_{0} = 0,

$\bar{\nabla} \times {\bar{E}}_{0} = 0,$

(1D.11)

\bar{\nabla} \times {\bar{H}}_{0} = {\bar{J}}_{0},

$\bar{\nabla} \times {\bar{H}}_{0} = {\bar{J}}_{0},$

(1D.12)

\bar{\nabla} \cdot {\bar{J}}_{0} = 0,

$\bar{\nabla} \cdot {\bar{J}}_{0} = 0,$

(1D.13)

\bar{\nabla} \times {\bar{E}}_{1} = - \frac{\partial {\bar{B}}_{0}}{\partial τ},

$\bar{\nabla} \times {\bar{E}}_{1} = - \frac{\partial {\bar{B}}_{0}}{\partial τ},$

(1D.14)

\bar{\nabla} \times {\bar{H}}_{1} = {\bar{J}}_{1} + \frac{\partial {\bar{D}}_{0}}{\partial τ},

$\bar{\nabla} \times {\bar{H}}_{1} = {\bar{J}}_{1} + \frac{\partial {\bar{D}}_{0}}{\partial τ},$

(1D.15)

\bar{\nabla} \cdot {\bar{J}}_{1} = - \frac{\partial ρ_{v 0}}{\partial τ} .

$\bar{\nabla} \cdot {\bar{J}}_{1} = - \frac{\partial ρ_{v 0}}{\partial τ} .$

We can generate higher-order sets of equations such as Equation 1D.13, Equation 1D.14 and Equation 1D.15. Note, however, from Equations 1D.5 and 1D.6, we obtain

(1D.16)

\bar{\nabla} \cdot {\bar{D}}_{k} = ρ_{v k}

$\bar{\nabla} \cdot {\bar{D}}_{k} = ρ_{v k}$

(1D.17)

\bar{\nabla} \cdot {\bar{B}}_{k} = 0, k = 0, 1, 2, \dots .

$\bar{\nabla} \cdot {\bar{B}}_{k} = 0, k = 0, 1, 2, \dots .$

1D.3Circuit Parameters R, L, and C

The circuit element R is identified as the zeroth-order solution of Equations 1D.10 and 1D.11. For a resistor R, the first-order electric and magnetic fields are negligible compared with the zeroth-order fields. Its characterization as a relationship between the zeroth-order electric and magnetic fields leads to the memoryless instantaneous relationship of a pure resistor. Its gross parameter representation is Ohm’s law given by

(1D.18)

V (t) = R I (t) .

$V (t) = R I (t) .$

If only the first-order magnetic field is negligible but the first-order electric field is not negligible, the system can be identified as a resistor in series with an inductor [2]. Its gross parameter representation is

(1D.19)

V (t) = R I (t) + L \frac{d I}{d t} .

$V (t) = R I (t) + L \frac{d I}{d t} .$

On the other hand, if only the first-order electric field is negligible but the first-order magnetic field is not negligible, the system can be identified as a resistor R (conductance G = 1/R) in parallel with a capacitor C. The gross parameter representation in this case is

(1D.20)

I (t) = G V (t) + C \frac{d V}{d t} .

$I (t) = G V (t) + C \frac{d V}{d t} .$

Equations 1D.19 and 1D.20 can be obtained and R, G, L, and C are calculated by using the integral form of the relevant Maxwell’s equations and the constitutive relations for the material:

(1D.21)

\bar{J} = σ \bar{E},

$\bar{J} = σ \bar{E},$

(1D.22)

\bar{B} = μ \bar{H},

$\bar{B} = μ \bar{H},$

(1D.23)

\bar{D} = ε \bar{E} .

$\bar{D} = ε \bar{E} .$

1D.4Memristor

Fano et al. [1] dismissed the case where the first-order fields ${\bar{E}}_{1}$ ${\bar{E}}_{1}$ and ${\bar{H}}_{1}$ ${\bar{H}}_{1}$ are not negligible saying that such a case is not relevant to circuit theory. Chua [2] suggested that such a case under approximate conditions leads to a two-terminal device where the charge q(t) (the surface integral of the first-order electric flux density vector ${\bar{D}}_{1}$ ${\bar{D}}_{1}$ ) is related to the flux Φ_m(t) (surface integral of the first-order ${\bar{B}}_{1}$ ${\bar{B}}_{1}$ field). The approximate conditions are: (i) both zeroth-order fields are negligible compared to the first-order fields; and (ii) the material of the device is nonlinear.

The nonlinear relationships are

(1D.24)

{\bar{J}}_{1} = J ({\bar{E}}_{1}),

${\bar{J}}_{1} = J ({\bar{E}}_{1}),$

(1D.25)

{\bar{B}}_{1} = B ({\bar{H}}_{1}),

${\bar{B}}_{1} = B ({\bar{H}}_{1}),$

(1D.26)

{\bar{D}}_{1} = D ({\bar{E}}_{1}),

${\bar{D}}_{1} = D ({\bar{E}}_{1}),$

(1D.27)

\bar{\nabla} \times {\bar{H}}_{1} = J ({\bar{E}}_{1}),

$\bar{\nabla} \times {\bar{H}}_{1} = J ({\bar{E}}_{1}),$

(1D.28)

{\bar{E}}_{1} = f ({\bar{H}}_{1}),

${\bar{E}}_{1} = f ({\bar{H}}_{1}),$

leading to

(1D.29)

{\bar{D}}_{1} = g ({\bar{B}}_{1}) .

${\bar{D}}_{1} = g ({\bar{B}}_{1}) .$

Equation 1D.29 gives the instantaneous (memoryless) relationship between ${\bar{D}}_{1}$ ${\bar{D}}_{1}$ and ${\bar{B}}_{1}$ ${\bar{B}}_{1}$ .

A physical memristor device is essentially an ac device; otherwise, the dc electromagnetic fields will give rise to nonnegligible zeroth-order fields.

In terms of gross variables and parameters we write

(1D.30)

V (t) = R I (t) = f_{R} (I),

$V (t) = R I (t) = f_{R} (I),$

(1D.31)

q (t) = C V (t) = f_{C} (V),

$q (t) = C V (t) = f_{C} (V),$

(1D.32)

Φ_{m} (t) = L I (t) = f_{L} (I) .

$Φ_{m} (t) = L I (t) = f_{L} (I) .$

In the case of a memristor

(1D.33)

Φ_{m} (t) = f_{M} (q) .

$Φ_{m} (t) = f_{M} (q) .$

For the case of a charge-controlled memristor

(1D.34)

\frac{d Φ_{m}}{d t} = \frac{d f_{M}}{d q} \frac{d q}{d t},

$\frac{d Φ_{m}}{d t} = \frac{d f_{M}}{d q} \frac{d q}{d t},$

(1D.35)

V (t) = \frac{d f_{M}}{d q} i (t),

$V (t) = \frac{d f_{M}}{d q} i (t),$

where

(1D.36)

\frac{d f_{M}}{d q} = M (q)

$\frac{d f_{M}}{d q} = M (q)$

is the incremental memristance (in the units of ohms).

The mathematical model for the HP memristor [3,4] which is based on its fabrication process is given by

M (q) = R_{OFF} (1 - \frac{R_{ON}}{β} q (t)),

$M (q) = R_{OFF} (1 - \frac{R_{ON}}{β} q (t)),$

where

β = \frac{D^{2}}{μ_{D}} (Wb) .

$β = \frac{D^{2}}{μ_{D}} (Wb) .$

Here, μ_D is the average drift mobility and D is the film (titanium dioxide) thickness. R_OFF and R_ON are the “OFF” and “ON” states of the resistance. The device is a TiO₂ junction where one side is doped with positive ions and the other side is undoped. The width w of the doped region depends on the charge passing through the device. The state equation describing process can be written as

\begin{matrix} \frac{1}{D} \frac{d w (t)}{d t} = \frac{R_{ON}}{β} i (t), \\ \frac{w (t)}{D} = \frac{w (t_{0})}{D} + \frac{q (t)}{Q_{D}}, \end{matrix}

$\begin{matrix} \frac{1}{D} \frac{d w (t)}{d t} = \frac{R_{ON}}{β} i (t), \\ \frac{w (t)}{D} = \frac{w (t_{0})}{D} + \frac{q (t)}{Q_{D}}, \end{matrix}$

where

Q_{D} = \frac{β}{R_{ON}} = i \times t .

$Q_{D} = \frac{β}{R_{ON}} = i \times t .$

Figure 1D.1 gives the symbol proposed in [1] and q versus Φ_m curve for the memristor.

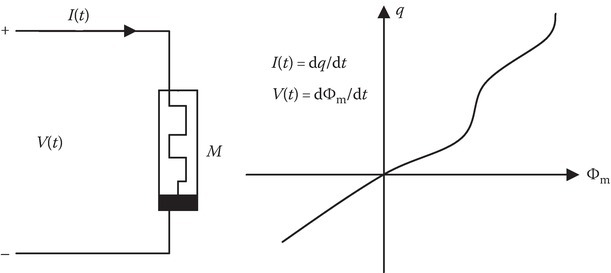
FIGURE 1D.1
Memristor and its Φ_m versus q curve.

Memristor is a passive two-terminal device. It cannot store energy, when V(t) = 0 and I(t) = 0. A memristor acts as a linear resistor when its frequency goes toward infinity and as a nonlinear resistor at low frequencies.

It has a regime of operation with an approximately linear charge–resistance relationship as the time integral of the current stays within certain bounds. Applications are in nanoelectronic memories, computer logic, and neuromorphic computer architectures.

In an ideal description, the element remembers the amount of current passing through it in the past. When the current stops, the component retains the last resistance that it had. When the flow of charge starts again, the resistance of the circuit will be what it was when it was last active.

In summary, unlike the resistor R whose value depends on the ratio of instantaneous voltage to current, in the case of memristor the resistance depends on the ratio of the integral of the input voltage to the integral of the input current.

Since ∫V dt = Φ_m and ∫I dt = q, it is the functional relationship between Φ_m and q that determines the properties of the memristor. If this relationship is linear, it is the same as the resistor R.

This is an active field of research with many potential applications and developments.

References

1.Fano, R. M., Chu, L. N., and Adler, R. B., Electromagnetic Fields, Energy, and Forces, Wiley, New York, 1960.
2.Chua, L. O., Memristor, the missing circuit element, IEEE Trans. Circ. Theory, CT-18(5), 507–519, 1971.
3.Strukov, D. B., Snider, G. S., Steward, D. R., and Williams, R. S., The missing memristor found, Nature, 453(7191), 80–83, 2008.
4.Kavehei, O., Iqbal, A., Kim, Y. S., Eshraghiam, K., Al-Sarawi, S. F., and Abbott, D., The fourth element: Characteristics, modeling and electromagnetic theory of the memristor, Proc. R. Soc. A, 466(2120), 2175–2202, 2010.

..................Content has been hidden....................

You can't read the all page of ebook, please click here login for view all page.

Table of Contents for Appendix 1D: Low-Frequency Approximation of Maxwell’s Equations R, L, C, and Memristor M

Create new playlist

Sign In

Sign Up

1D.1Introduction

1D.2Time-Rate Parameter

1D.3Circuit Parameters R, L, and C

1D.4Memristor

References

Table of Contents for
Appendix 1D: Low-Frequency Approximation of Maxwell’s Equations R, L, C, and Memristor M