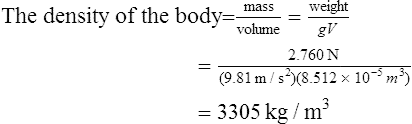U-tube manometer

6. A manometer is a device used for measuring relatively small pressures, either above or below atmospheric pressure. A simple U-tube manometer is shown in Figure 44.3. Pressure p acting in, say a gas main, pushes the liquid in the U-tube until equilibrium is obtained. At equilibrium: pressure in gas main, p = (atmospheric pressure, p_a) + (pressure due to the column of liquid, ρgh) i.e., p = p_a + ρgh.

Thus, for example, if the atmospheric pressure, p_a is 101 kPa, the liquid in the U-tube is water of density 1000 kg/m³ and height, h is 300 mm, then

$\begin{array}{l}\mathrm{absolute}\mathrm{gas}\mathrm{pressure}=\left(101000+1000\times 9.8\times 0.3\right)\mathrm{Pa}\\ =\left(101000+2940\right)\mathrm{Pa}\\ 103940\mathrm{Pa}=103.94\mathrm{kPa}.\end{array}$

The gauge pressure of the gas is 2.94 kPa.

By filling the U-tube with a more dense liquid, say mercury having a density of 13 600 kg/m³, for a given height of U-tube, the pressure which can be measured is increased by a factor of 13.6.

By inclining one limb of the U-tube, as shown in Figure 44.4, greater sensitivity is achieved, that is, there is a larger movement of the liquid for a given change in pressure when compared with a U-tube having vertical limbs. An inclined manometer normally has a reservoir of sufficient area to give virtually a constant level in the left-hand limb. From Figure 44.4, it can be seen that pressure p applied to the reservoir causes a scale change of ‘l’ in the inclined manometer compared with ‘h’ in a normal manometer.

Simple barometer

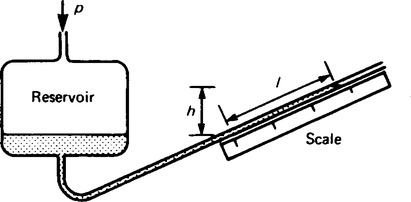
7. A simple barometer consists of a length of glass tubing, approximately 800 mm long and sealed at one end, which is filled with mercury and then inverted in a beaker of mercury, as shown in Figure 44.5. At equilibrium, the atmospheric pressure, p_a, is tending to force the mercury up the tube, whilst the force due to the column of mercury is tending to force the mercury out of the tube, i.e. p_a = ρgh. As the atmospheric pressure varies, height h varies, giving an indication on the scale of the atmospheric pressure.

Fortin barometer

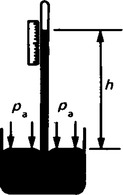
8. The Fortin barometer is as shown in Figure 44.6. Mercury is contained in a leather bag at the base of the mercury reservoir, and height, H, of the mercury in the reservoir can be adjusted using the screw at the base of the barometer to depress or relase the leather bag. To measure the atmospheric pressure, the screw is adjusted until the pointer at H is just touching the surface of the mercury and the height of the mercury column is then read using the main and vernier scales. The measurement of atmospheric pressure using a Fortin barometer is achieved much more accurately than by using a simple barometer.

Bourdon pressure gauge

9. The main components of a Bourdon pressure gauge are shown in Figure 44.7. When pressure, p, is applied to the curved phosphor bronze tube, which is sealed at A, it tends to straighten, moving A to the right. Conversely, a decrease in pressure below that due to the atmosphere moves point A to the left. When A moves to the right, B moves to the left, rotating the pointer across a scale. This type of pressure gauge can be used to measure large pressures and pressures both above and below atmospheric pressure. The Bourdon pressure gauge indicates gauge pressure and is very widely used in industry for pressure measurements.

Hydrostatic pressure

10. The pressure at the base of the tank shown in Figure 44.8(a) is:

$p=\rho gh=wh,$

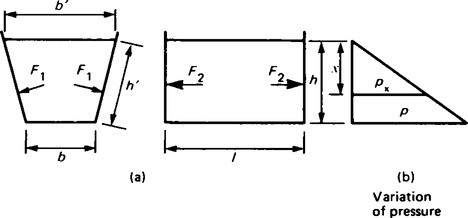
    where w is the specific weight, i.e. the weight per unit volume, its unit being N/m³.

The pressure increases to this value uniformly from zero at the free surface. The pressure variation is shown in Figure 44.8(b).

At any intermediate depth x the pressure is

$p_x=\rho gx=wx.$

It may be shown that the average pressure on any wetted plane surface is the pressure at the centroid, the centre of area. The sloping sides of the tank of Figure 44.8 are rectangular and therefore the average pressure on them is the pressure at half depth:

$\frac{p}{2}=\frac{\rho gh}{2}=\frac{wh}{2}$

The force on a sloping side is the product of this average pressure and the area of the sloping side:

$F_1=\frac{\rho gh}{2}\times l{h}^{\prime }=\frac{whl{h}^{\prime }}{2}$

where h’ is the slant height. The pressure and consequently the forces F₁ are at right angles to the sloping sides as shown in Figure 44.8.

The average pressure on the vertical trapezoidal ends of the tank is not the pressure at half depth. This is because the centroid of an end is not at half depth — it is rather higher. The depth of the centroid is given by:

$\frac{h}{3}\left(\frac{2b+b^{\prime }}{b+b^{\prime }}\right),$

(see Figure 44.8)

The average pressure on an end is therefore:

$\frac{\rho gh}{3}\left(\frac{2b+b^{\prime }}{b+b^{\prime }}\right)=\frac{wh}{3}\left(\frac{2b+b^{\prime }}{b+b^{\prime }}\right)$

The forces F₂ on the vertical trapezoidal ends of the tank are horizontal forces given by the product of this average pressure and the area of the trapezium,

$\left(\frac{2b+b^{\prime }}{2}\right)h.$

The force on the base of the tank is (ρgh)x (area of base) = ρhlb = whlb

For a tank with vertical sides this is the weight of liquid in the tank.

11. In any vessel containing homogeneous liquid at rest and in continuous contact, the pressure must be the same at all points at the same level. In a U-tube, as shown in Figure 44.9, with the liquid in the lower part at rest, the pressure must be the same on both sides for all levels up to X₁X₂. The pressure at X₁, however, is greater than the pressure at Y₁ by an amount p₁ = w₁h = ρ₁gh, where w₁,ρ₁, ρ₁ are the specific weight and density respectively of the liquid, or gas, between X₁ and Y₁.

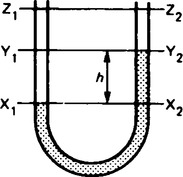
Similarly, the pressure at X₂ is greater than the pressure at Y₂ by an amount given by p₂ = w₂h = ρ₂gh, where w₂, ρ₂ are the specific weight and density respectively of the liquid in the bottom of the U-tube.

For practical reasons ρ₂ must be greater than ρ₁ and the pressure at Y₁ will exceed that at Y₂ by

$p_2-p_1=\left(w_2-w_1\right)h=\left({\rho }_2-{\rho }_1\right)gh.$

If the upper limits of the U-tube contain air or any other gas or gas mixture w₁ and ρ₁ can reasonably be ignored, giving

$p_2-p_1=w_{2}h={\rho }_{2}gh$

If the upper limbs contain a lighter liquid, then the pressure difference may be expressed as

$p_2-p_1={\rho }_1\left(d-1\right)gh=\left(d-1\right)w_{1}h\mathrm{where}d=\frac{{\rho }_2}{{\rho }_1}$

A common arrangement is mercury and water, in which case d is the relative density of mercury approximately 13.6. This gives:

$p_2-p_1=12.6\rho gh=12.6wh,$

ρ and w being respectively, the density and specific weight of water. The pressure difference at Z₁Z₂ will be the same as at Y₁Y₂ if both limbs contain the same liquid between these levels. This follows from the fact that the pressure increase from Z₁ to Y₁ is the same as the increase from Z₂ to Y₂.

Archimedes’ principle

If ρ is known and W obtained from a simple experiment, V can be calculated. Hence the density of the solid body can be calculated. If V is known and W obtained, ρ can be calculated.

If a body floats on the surface of a liquid all of its weight appears to have been lost. The weight of liquid displaced is equal to the weight of the floating body.

For example, a body weighs 2.760 N in air and 1.925 N when completely immersed in water of density 1000 kg/m³.

Hence the apparent loss of weight is

$2.760\text{N}-1.925\text{N}=0.835\text{N}.$

This is the weight of water displaced, i.e. Vρg, where V is the volume of the body and ρ is the density of water.

Thus 0.835 N = (V) (1000 kg/m³) (9.81 m/s²)

from which, volume,

$V=\frac{0.835}{9810}=8.512\times {10}^{-5}{\text{m}}^3$

$\begin{array}{l}\text{The density of the body=}\frac{\mathrm{mass}}{\mathrm{volume}}\text{=}\frac{\mathrm{weight}}{gV}\\ \text{=}\frac{2.760\text{N}}{\left(9.81\text{m}/{\text{s}}^2\right)\left(8.512\times {10}^{-5}{m}^3\right)}\\ =3305\mathrm{kg}/{\text{m}}^3\end{array}$

$\text{Relative density=}\frac{\mathrm{density}}{\mathrm{density}\mathrm{of}\mathrm{water}}\text{=}\frac{3305}{1000}=3.305$