5.2 Principal Ideal Domains
1. No. 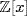 is a subring of the PID
is a subring of the PID 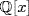 , but
, but 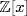 is not a PID (Example 3).
is not a PID (Example 3).
3. The ideals are 0 = 0 and F =
0 and F =  1 , both principal.
1 , both principal.
4. No. If it were a PID it would be a UFD by Theorem 1, contrary to Example 5 §5.1.
5. Let A =  a , a ≠ 0. If a is a unit then |R/A| = 1. Otherwise, by Theorem 4 §3.3, let B/A be any ideal of R/A, say B =
a , a ≠ 0. If a is a unit then |R/A| = 1. Otherwise, by Theorem 4 §3.3, let B/A be any ideal of R/A, say B =  b. Then
b. Then  a
a ⊆
⊆  b so b|a. Since a has a prime factorization, there are at most finitely many such divisors b of a up to associates, and hence only finitely many ideals
b so b|a. Since a has a prime factorization, there are at most finitely many such divisors b of a up to associates, and hence only finitely many ideals  b.
b.
6. a. No. 0 is a prime ideal of  is an integral domain) but 0 is not maximal.
is an integral domain) but 0 is not maximal.
7. (c) ⇒ (a). Assume (c). If a ≠ 0 in R consider A = {ra + gx  r
r  R, g
R, g  R[x]}. This is an ideal of R[x] so let A =
R[x]}. This is an ideal of R[x] so let A = f by (c). Then x
f by (c). Then x  A implies that f|x so f
A implies that f|x so f  1 or f
1 or f  x. Thus A = R[x] or A =
x. Thus A = R[x] or A =  x. But A =
x. But A = x is impossible because a
x is impossible because a  A would then imply x|a. So 1
A would then imply x|a. So 1  A, say 1 = ra + gx. Clearly then g = 0, so a is a unit. This proves (c) ⇒ (a).
A, say 1 = ra + gx. Clearly then g = 0, so a is a unit. This proves (c) ⇒ (a).
8.
a. Write 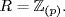 R is a subring of R because
R is a subring of R because  ,
, 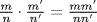 and
and 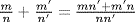 and p does not divide nn′. Thus R is an integral domain. Given
and p does not divide nn′. Thus R is an integral domain. Given 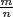 in R, if p does not divide m then
in R, if p does not divide m then 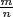 is a unit in R (with inverse
is a unit in R (with inverse 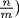 . Conversely, if
. Conversely, if 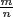 is a unit, say
is a unit, say 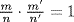 , then mm′ = nn′ so p does not divide m (it does not divide n or n′), so
, then mm′ = nn′ so p does not divide m (it does not divide n or n′), so 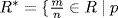 does not divide m}.
does not divide m}.
c. R is a PID by (b) and the fact that 0 =  0 . By (b), the ideals of R are 0 and R =
0 . By (b), the ideals of R are 0 and R = 1 ⊃
1 ⊃  p ⊃
p ⊃  p2 ⊃
p2 ⊃  . Clearly
. Clearly  p
p is the only maximal ideal.
is the only maximal ideal.
9. If a ≠ 0 in 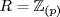 , let
, let  a
a =
=  pk where
pk where 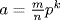 , p does not divide m or n (see (b) of the preceding exercise). Thus δ is well defined by δ(a) = k. If a, b ≠ 1 are given, we want a = qb + r in R where r = 0 or δ(r) < δ(b). Let δ(a) = k and δ(b) = m so a = upk, b = vpm where u,
, p does not divide m or n (see (b) of the preceding exercise). Thus δ is well defined by δ(a) = k. If a, b ≠ 1 are given, we want a = qb + r in R where r = 0 or δ(r) < δ(b). Let δ(a) = k and δ(b) = m so a = upk, b = vpm where u, 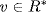 . If k < m then a = 0b + a does it because δ(a) = k < m = δ(b). If k ≥ m then
. If k < m then a = 0b + a does it because δ(a) = k < m = δ(b). If k ≥ m then
![]()
so a = qb + 0 in this case. Hence δ is a division function on R. Note: a = upk, u  R∗. If b = vpm then ab = uvpm+k so
R∗. If b = vpm then ab = uvpm+k so
![]()
Also, if k ≤ m, a + b = (u + vpm−k)pk = wpk+t, 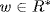 . Thus
. Thus
![]()
In particular, if a ≠ 0 ≠ b then δ(ab) = δ(a) + δ(b) ≥ δ(a) . This proves that R is a euclidean domain.
11. a.
1. If a = m + nω then aa∗ = (m + nω)(m − nω) = m2 − ω2n2 = N(a). Similarly N(a∗) = aa∗.
2. If b = p + qω then ab = (mp + nqω2) + (mq + np)ω and
![]()
Clearly (a∗)∗ = (m − nω)∗ = m + nω = a.
13. a. It suffices to verify Lemma 1. Given r, s in 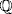 let m and n be the integers closest to r and s. Then
let m and n be the integers closest to r and s. Then  and
and 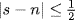 so
so
![]()
14. a. Given r, 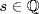 , let m, n be the closest integers, so that
, let m, n be the closest integers, so that
![]()
Case 1. (r − m)2 ≤ 2(s − n)2. Then
![]()
Case 2. (r − m)2 > 2(s − n)2. Then
![]()
This verifies Lemma 1.
15. a. As in (a) of the preceding exercise, 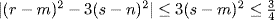 or
or 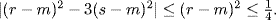
17. If a = qb + r where r = 0 or δ(r) < δ(b), then
![]()
18. a. Define δ(a) = 1 for all a  F. Then δ(ab) = 1 = δ(a) proves E. As to DA, if a, b ≠ 0 are in F then a = (ab−1)b + 0.
F. Then δ(ab) = 1 = δ(a) proves E. As to DA, if a, b ≠ 0 are in F then a = (ab−1)b + 0.
19. Let a = ub, a a unit. Then δ(a) = δ(ub) ≥ δ(b) by E. Similarly b = u−1a implies δ(b) ≥ δ(a), so δ(b) = δ(a).
21. We always have δ(ab) ≥ δ(a) by E. Assume b is a nonunit. If δ(ab) = δ(a), write c = ab. Then a|c and δ(a) = δ(c) so, by the preceding exercise, a  c, say c = ua, u a unit. Thus ab = ua so b = u is a unit, contrary to assumption. Conversely, assume δ(ab) > δ(a). If b is a unit then ab
c, say c = ua, u a unit. Thus ab = ua so b = u is a unit, contrary to assumption. Conversely, assume δ(ab) > δ(a). If b is a unit then ab  a so δ(ab) = δ(a) by Exercise 19. So b is a nonunit.
a so δ(ab) = δ(a) by Exercise 19. So b is a nonunit.
23. a. Let P = p be as given. If a
p be as given. If a  P then a is a nonunit, as P ≠ R. If a is a nonunit, then A =
P then a is a nonunit, as P ≠ R. If a is a nonunit, then A =  a ≠ R so (by Exercise 6), A ⊆ P. Then a
a ≠ R so (by Exercise 6), A ⊆ P. Then a  P.
P.
24. a. Write a = 1 + i. Then N(a) = 12 + 1 = 2 is a prime in 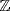 , so a is irreducible in
, so a is irreducible in 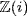 by Theorem 5, and so R/A is a field by Theorems 7, 4 and 3. The preceding exercise shows that R/A is a finite field. Now δ(a) = N(a) so if r = m + ni has δ(r) = m2 + n2 < 2, then r = 0, ±1, ±i, so
by Theorem 5, and so R/A is a field by Theorems 7, 4 and 3. The preceding exercise shows that R/A is a finite field. Now δ(a) = N(a) so if r = m + ni has δ(r) = m2 + n2 < 2, then r = 0, ±1, ±i, so
![]()
However i + A = − 1 + Aand −i + A = 1 + A, so
![]()
But 1 + A = − 1 + A because 2 = (1 − i)(1 + i)  A. So
A. So
![]()
is the field of two elements.
25. It is clear that 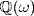 is a subring of
is a subring of 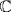 and that
and that 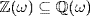 . We show that
. We show that 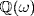 is a field, and that
is a field, and that  , b ≠ 0 in
, b ≠ 0 in 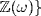 . If 0 ≠ q = r + sω is in
. If 0 ≠ q = r + sω is in 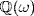 then N(q) = qq∗ = r2 − s2ω2 ≠ 0 as
then N(q) = qq∗ = r2 − s2ω2 ≠ 0 as  . Since
. Since
![]()
and we have shown that 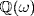 is a field. Now let
is a field. Now let 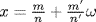 in
in 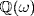 . Then
. Then 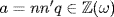 so q = ab−1 where
so q = ab−1 where 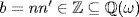 .
.
26. a. (1) ⇒ (2). Given a ≠ 0, b ≠ 0, let Ra + Rb =  d. Then d = ra + sb for some r, s
d. Then d = ra + sb for some r, s  R, so if k|a and k|b in R then k|d. But d|a and d|b because a, b
R, so if k|a and k|b in R then k|d. But d|a and d|b because a, b 
 d. Thus d = gcd (a, b) . (2) ⇒ (1). Given A = Ra + Rb, clearly A is principal if a = 0 or b = 0. Otherwise, by (2) let d = gcd (a, b)
d. Thus d = gcd (a, b) . (2) ⇒ (1). Given A = Ra + Rb, clearly A is principal if a = 0 or b = 0. Otherwise, by (2) let d = gcd (a, b)  d where d = ra + sb for r, s
d where d = ra + sb for r, s  R. Then d
R. Then d  A so
A so  d ⊆ A. On the other hand, d|a and d|b so a
d ⊆ A. On the other hand, d|a and d|b so a
 d and b
d and b 
 d. Hence Ra + Rb ⊆
d. Hence Ra + Rb ⊆  d.
d.
27. If R is a PID, we must show that R satisfies the ACCP. This follows by the first part of the proof of Theorem 1. Conversely, if R satisfies the conditions, every finitely generated ideal of R is principal by Exercise 26(b). If A is a non-finitely generated ideal of R, then A ≠ 0 so let a1  A. Then A≠
A. Then A≠  a1 so let a2
a1 so let a2 A −
A −  a1 so that Ra1 ⊂ Ra1 + Ra2. ButA ≠ Ra1 + Ra2 so let a3 ∉ Ra1 + Ra2. Thus Ra1 ⊂ Ra1 + Ra2 ⊂ Ra1 + Ra2 + Ra3. This process continues to give a strictly increasing chain of principal ideals, contrary to the ACCP.
a1 so that Ra1 ⊂ Ra1 + Ra2. ButA ≠ Ra1 + Ra2 so let a3 ∉ Ra1 + Ra2. Thus Ra1 ⊂ Ra1 + Ra2 ⊂ Ra1 + Ra2 + Ra3. This process continues to give a strictly increasing chain of principal ideals, contrary to the ACCP.
29. Write B = b and C =
b and C =  c. By Theorem 8 §3.4, it suffices to show that B∩ C =
c. By Theorem 8 §3.4, it suffices to show that B∩ C =  a and B + C = R. Now gcd (b, c) = 1 means that 1 = rb + sc for some r, s = R. Thus 1
a and B + C = R. Now gcd (b, c) = 1 means that 1 = rb + sc for some r, s = R. Thus 1  B + C, so B + C = R. It is clear that
B + C, so B + C = R. It is clear that
![]()
If x  B ∩ C then b|x and c|x, say x = b′b = c′c. Then 1 = rb + sc gives x = rbx + scx = rb(c′c) + scb′b = (rc′ + sb′)bc = (rc′ + sb′)a
B ∩ C then b|x and c|x, say x = b′b = c′c. Then 1 = rb + sc gives x = rbx + scx = rb(c′c) + scb′b = (rc′ + sb′)bc = (rc′ + sb′)a 
 a.
a.
31. Let  be a unit in
be a unit in 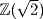 , so that
, so that 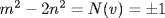 . Since 1 < u we have 0<
. Since 1 < u we have 0<  < u−3 < u−2 < u−1 < u0 = 1 < u < u2 < u3 <
< u−3 < u−2 < u−1 < u0 = 1 < u < u2 < u3 <  . Since u−k approaches 0 for large k, either
. Since u−k approaches 0 for large k, either 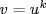 for
for 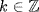 or
or 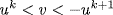 . But the latter possibility implies 1 < vu−k < u where vu−k is a unit. We rule this out below, so
. But the latter possibility implies 1 < vu−k < u where vu−k is a unit. We rule this out below, so  . If
. If  then
then 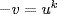 in the same way. Claim.
in the same way. Claim.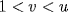 is impossible for a unit
is impossible for a unit 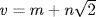 in
in 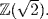 Proof. vv∗ = ± 1 so
Proof. vv∗ = ± 1 so 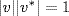 . But
. But 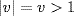 so
so 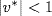 , that is
, that is
![]()
Since also 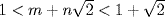 , adding these inequalities gives
, adding these inequalities gives
![]()
Hence m = 1 and so 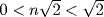 . This is impossible as n is an integer.
. This is impossible as n is an integer.
32. Write a = m + nω, b = p + qω and 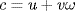 where m, n, p, q, u and
where m, n, p, q, u and  are in
are in 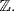
a.  a, b = mp − nqω2 =
a, b = mp − nqω2 =  b, a.
b, a.
b.  ka, b = (km)p − (kn)qω2 = k(mp − nqω2) = k
ka, b = (km)p − (kn)qω2 = k(mp − nqω2) = k  a, b.
a, b.
33. No. If so, write 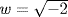 . Then
. Then 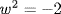 so −2 > 0 by Lemma 1 §3.5. But 1 > 0 so 2 = 1 + 1 > 0, whence −2 < 0 by Axiom P2. This is a contradiction.
so −2 > 0 by Lemma 1 §3.5. But 1 > 0 so 2 = 1 + 1 > 0, whence −2 < 0 by Axiom P2. This is a contradiction.
34. a. Clearly θ(a + b) = θ(a) + θ(b) and θ(1) = 1. We have
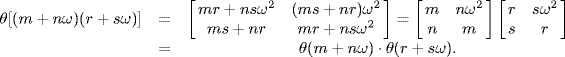
Clearly ker θ = 0, so θ is one-to-one.
35. a. We have τ(ab) = (ab)∗ = a∗b∗ = τ(a) · τ(b) by Theorem 5. If a = m + nω and b = p + qω. Then
![]()
Since τ(1) = 1∗ = 1 this shows τ is a ring homomorphism. But a∗∗ = a for all a shows τ2 = 1R so τ−1 = τ. Thus τ is an isomorphism.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
