2.10 The Isomorphism Theorem
1. Define  by
by 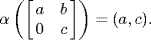 This is a group homomorphism by direct calculation. We have
This is a group homomorphism by direct calculation. We have  if and only if a = 1 = c, so ker α = K.
if and only if a = 1 = c, so ker α = K.
3. Since  , H G and G/H = {H, G H} is a group with H as unity. Thus σ : G/H → {1, − 1} is an isomorphism if σ(H) = 1 and σ(G − H) = − 1. Let ϕ : G → G/H be the coset map ϕ(g) = Hg, and let α = σϕ : G → {1, − 1}. Then α is a homomorphism and: If g
, H G and G/H = {H, G H} is a group with H as unity. Thus σ : G/H → {1, − 1} is an isomorphism if σ(H) = 1 and σ(G − H) = − 1. Let ϕ : G → G/H be the coset map ϕ(g) = Hg, and let α = σϕ : G → {1, − 1}. Then α is a homomorphism and: If g  H, then α(g) = σϕ(g) = σ(H) = 1; if g ∉ H, then α(g) = σϕ(g) = σ(G − H) = − 1.
H, then α(g) = σϕ(g) = σ(H) = 1; if g ∉ H, then α(g) = σϕ(g) = σ(G − H) = − 1.
4.
a. We have 1  α−1(X) because α(1) = 1
α−1(X) because α(1) = 1  X. If g, h
X. If g, h  α−1(X), then α(g)
α−1(X), then α(g)  X and α(h)
X and α(h)  X, so α(g−1) = [α(g)]−1
X, so α(g−1) = [α(g)]−1  X and α(gh) = α(g) · α(h)
X and α(gh) = α(g) · α(h)  X. Thus g−1
X. Thus g−1  α−1(X) and gh
α−1(X) and gh  α−1(X), so α−1(X) is a subgroup of G. If X α(G), let g
α−1(X), so α−1(X) is a subgroup of G. If X α(G), let g  α−1(X), a
α−1(X), a  G. Then
G. Then
![]()
Thus a−1ga  α−1(X) for all a
α−1(X) for all a  G; that is α−1(X) G.
G; that is α−1(X) G.
c. Since X ∩ Y ⊆ X and X ∩ Y ⊆ Y, α−1(X ∩ Y) ⊆ α−1(X) ∩ α−1(Y) by (b). If g  α−1(X) ∩ α−1(Y), then α(g)
α−1(X) ∩ α−1(Y), then α(g)  X and α(g)
X and α(g)  Y, so α(g)
Y, so α(g)  X ∩ Y. Hence g
X ∩ Y. Hence g  α−1(X ∩ Y).
α−1(X ∩ Y).
5.
a. If gd = 1, then since d  m, 1 = gm = ρmg, so g
m, 1 = gm = ρmg, so g  ker ρm. Conversely, if ρmg = 1, then gm = 1. We have also that gn = 1 (since
ker ρm. Conversely, if ρmg = 1, then gm = 1. We have also that gn = 1 (since  . Since d = xm + yn,
. Since d = xm + yn,  , this gives gd = (gm)x(gn)y = 1x1y = 1.
, this gives gd = (gm)x(gn)y = 1x1y = 1.
c. Let  where o(a) = n. If σ : G → G is an automorphism then o(σ(a)) = o(a) = n. Hence Theorem 8, §2.4 gives σ(a) = am where gcd(m, n) = 1 . Now let g
where o(a) = n. If σ : G → G is an automorphism then o(σ(a)) = o(a) = n. Hence Theorem 8, §2.4 gives σ(a) = am where gcd(m, n) = 1 . Now let g  G, say g = ak. Then
G, say g = ak. Then
![]()
It follows that σ = ρm.
7. Let α : G → G and let ker α = X
X  and α(G) =
and α(G) = Y
Y  where X and Y are finite sets. Since Y ⊆ α(G), let Z ⊆ G be a finite set such that, if y
where X and Y are finite sets. Since Y ⊆ α(G), let Z ⊆ G be a finite set such that, if y  Y, y = α(z) for some z
Y, y = α(z) for some z  Z. If g
Z. If g  G, then α(g)
G, then α(g)
 Y
Y  , so
, so
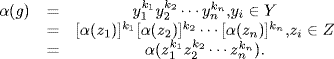
If we write 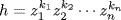 , then gh−1
, then gh−1  ker α, so
ker α, so 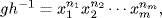 xi
xi  X. Hence
X. Hence
![]()
Hence G = X ∪ Z
X ∪ Z  , so since X ∪ Z a finite set, G is finitely generated.
, so since X ∪ Z a finite set, G is finitely generated.
8.
a. Let C6 =  g
g  , o(g) = 6, and write K4 = {1, a, b, ab}, where a2 = b2 = 1 and ab = ba. If α : C6 → K4 is a homomorphism, then α is determined by the choice of α(g) in K4. If α(g) = 1 then α is trivial (α(x) = 1 for all x
, o(g) = 6, and write K4 = {1, a, b, ab}, where a2 = b2 = 1 and ab = ba. If α : C6 → K4 is a homomorphism, then α is determined by the choice of α(g) in K4. If α(g) = 1 then α is trivial (α(x) = 1 for all x  G) . If α(g) = a (say), then α(gk) = ak. If we defineα by α(gk) = ak, it is well defined because
G) . If α(g) = a (say), then α(gk) = ak. If we defineα by α(gk) = ak, it is well defined because
![]()
Thus α is well defined, it is clearly a homomorphism. In the same way, there is a homomorphism carrying g to 1, a, b and ab; so there are four in all.
c. Let D3 = {1, a, a2, b, ba, ba2} where o(a) = 3, o(b) = 2, aba = b; and let C4 = c
c  , o(c) = 4. If α : D3 → C4, then o(α(a)) divides o(a) = 3, so α(a) = 1 because C4 has no element of order 3. Similarly o(α(b)) divides o(b) = 2, so α(b) = 1, c2. If α(b) = 1, then α is trivial. If α(b) = c2, then α(bkam) = c2k1m = c2k. If we now defineα by this formula, it is possible (but tedious) to check it is well defined and a homomorphism. There is another way. Write H =
, o(c) = 4. If α : D3 → C4, then o(α(a)) divides o(a) = 3, so α(a) = 1 because C4 has no element of order 3. Similarly o(α(b)) divides o(b) = 2, so α(b) = 1, c2. If α(b) = 1, then α is trivial. If α(b) = c2, then α(bkam) = c2k1m = c2k. If we now defineα by this formula, it is possible (but tedious) to check it is well defined and a homomorphism. There is another way. Write H = a
a  in D3. Then H D3 being of index 2, so D3/H = {H, bH}. Then there is an isomorphism {H, bH} → σ{1, c2} ⊆ C4 where σ(H) = 1, σ(bH) = c2. If ϕ : D3 → D3/H is the coset map, we get
in D3. Then H D3 being of index 2, so D3/H = {H, bH}. Then there is an isomorphism {H, bH} → σ{1, c2} ⊆ C4 where σ(H) = 1, σ(bH) = c2. If ϕ : D3 → D3/H is the coset map, we get
![]()
Then: σϕ(bkam) = σ(bkamH) = σ(bkH) = σ[(bH)k] = [σ(bH)]k = c2k. Hence the map we want is α = σϕ. This is the only non-trivial homomorphism.
9. No. If α : S4 → A4 has ker α = K = {ε, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)}, then A4/K ≅ α(A4). Now S4/K ≅ D3 [if a = K(1 2 3) and b = K(1 2), then o(g) = 3, o(b) = 2 and aba = b]. Hence α(S4) would be a subgroup of A4 which is isomorphic to D3. But there is no such subgroup: If o(σ) = 3 and o(τ) = 2 and στσ = τ, then σ is a 3-cycle, say σ = (1 2 3), and τ is one of (1 2)(3 4), (1 3)(2 4) or (1 4)(2 3). It is easy to check that στσ ≠ τ in each case.
10.
a.No. If α : S3 → K4 is onto, then K4 ≅ S3/ker α, so  would divide
would divide 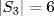 , a contradiction.
, a contradiction.
c. Yes. If S3 = {ε, σ, σ2, τ, τσ, τσ2}, let K = σ
σ  . Then
. Then  , so S3/K = {K, τ(K)}. If C2 =
, so S3/K = {K, τ(K)}. If C2 = c
c  , o(c) = 2, then S3 → S3/K → C3 is onto, where σ(K) = 1, σ[τ(K)] = c. Thus α = σϕ : S3 → C2 is given by
, o(c) = 2, then S3 → S3/K → C3 is onto, where σ(K) = 1, σ[τ(K)] = c. Thus α = σϕ : S3 → C2 is given by
![]()
11.
a. We have θ(gh) = (gh, gh) = (g, g)(h, h) = θ(g) · θ(h) for all g, h  G, so θ is a homomorphism. If θ(g) = (1, 1), then g = 1, so θ is one-to-one.
G, so θ is a homomorphism. If θ(g) = (1, 1), then g = 1, so θ is one-to-one.
b. (1) ⇒ (3). If G is abelian, define ϕ : G × G → G by ϕ(g, h) = gh−1. Then
![]()
Thus ϕ is a homomorphism, and ϕθ(g) = ϕ(g, g) = gg−1 = 1 for all g. Hence θ(G) ⊆ ker ϕ. If (g, h)  ker ϕ, then gh−1 = ϕ(g, h) = 1, so h = g. Thus (g, h)
ker ϕ, then gh−1 = ϕ(g, h) = 1, so h = g. Thus (g, h)  θ(G), so a(G) = ker ϕ.
θ(G), so a(G) = ker ϕ.
13. Let G be simple. If α : G → G1 is a nontrivial homomorphism, then ker α ≠ G. Since ker α G, ker α = {1} by simplicity, that is α is one-to-one. Hence G ≅ α(G) ⊆ G1.
Conversely, if G1 has a subgroup G0 and σ : G → G0 is an isomorphism, then σ : G → G1 is a (one-to-one) homomorphism, which is nontrivial because G0 ≠ {1}, being simple.
15. We have G/Z(G) ≅ inn G, and inn G is cyclic by hypothesis (a subgroup of aut G). Hence G is abelian by Theorem 2 §2.9. Thus τ : G → G is an automorphism where τ(g) = g−1 for all g  G. Write aut G =
G. Write aut G = σ
σ  . Then σk = τ for some k, so σ2k = τ2 = ε. Thus o(σ) is finite, that is
. Then σk = τ for some k, so σ2k = τ2 = ε. Thus o(σ) is finite, that is  is finite. Since o(τ) = 2 divides
is finite. Since o(τ) = 2 divides  , we are done.
, we are done.
17. a. If g  G′, g = [a1, b1][a2, b2]
G′, g = [a1, b1][a2, b2]  [an, bn] where [a, b] = a−1b−1ab is a commutator. Then
[an, bn] where [a, b] = a−1b−1ab is a commutator. Then
![]()
19. a.Define  by α(A) = det A. Then
by α(A) = det A. Then  because det A ≠ 0 if A is invertible, and α is a homomorphism because det AB = det A · det B. Since ker α = K, we get
because det A ≠ 0 if A is invertible, and α is a homomorphism because det AB = det A · det B. Since ker α = K, we get  .
.
21. Define 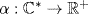 by
by  for
for  [Note that
[Note that  because z ≠ 0.] Then α is a homomorphism because
because z ≠ 0.] Then α is a homomorphism because  , and
, and 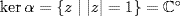 . Thus
. Thus  by the isomorphism theorem.
by the isomorphism theorem.
23. If a ≠ 0, then τa,b is a bijection, so  . We have
. We have  and
and  , and
, and  , so G is a subgroup. Now define
, so G is a subgroup. Now define 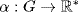 by (τa,b) = a. Then α is well defined: If
by (τa,b) = a. Then α is well defined: If  then ax + b = a′x + b′ for all x, so a = a′. Now
then ax + b = a′x + b′ for all x, so a = a′. Now
![]()
so α is a homomorphism. Since ker α = K, we have K G and 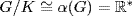 .
.
25. Define α : G × G × G → G × G by α(a, b, c) = (ac−1, bc−1). Then α is a homomorphism because G is abelian:
![]()
Now
![]()
Hence, since α is onto, we are done by the isomorphism theorem.
27. Define β : α(G) → G/K by β[α(g)] = Kg. This is well defined because α(g) = α(g1) implies 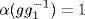 , so
, so  , that is Kg = Kg1. It is a homomorphism because
, that is Kg = Kg1. It is a homomorphism because
![]()
Finally
![]()
Thus α(K) α(G) and α(G)/α(K) ≅ α(G) = G/K. Note: This can also be solved by verifying α(K) α(G) directly, defining γ : G → α(G)/α(K) by γ(g) = [α(K)]α(g), and showing ker γ = K.
29. a. If 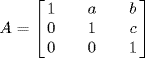 and
and 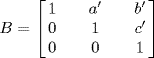 then
then  and
and 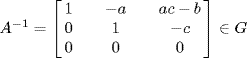 . Thus G is a subgroup of
. Thus G is a subgroup of 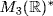 . The center consists of all
. The center consists of all  with b′ + ac′ + b = b + a′c + b′ for all a, b, c. Taking a = 1, c = 0 gives c′ = 0; taking a = 0, c = 1 gives a′ = 0. Thus
with b′ + ac′ + b = b + a′c + b′ for all a, b, c. Taking a = 1, c = 0 gives c′ = 0; taking a = 0, c = 1 gives a′ = 0. Thus  . The map
. The map  is an isomorphism
is an isomorphism 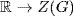 .
.
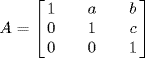 and
and 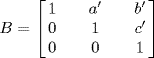 then
then  and
and 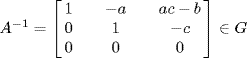 . Thus G is a subgroup of
. Thus G is a subgroup of  with b′ + ac′ + b = b + a′c + b′ for all a, b, c. Taking a = 1, c = 0 gives c′ = 0; taking a = 0, c = 1 gives a′ = 0. Thus
with b′ + ac′ + b = b + a′c + b′ for all a, b, c. Taking a = 1, c = 0 gives c′ = 0; taking a = 0, c = 1 gives a′ = 0. Thus  . The map
. The map  is an isomorphism
is an isomorphism 31. Let 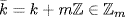 and
and  . Define
. Define  by
by  . Then
. Then  so α is a homomorphism. Now
so α is a homomorphism. Now
![]() and
and ![]() and
and ![]() .
.
Thus ![]() , so
, so ![]() .
.
33.
a.  has subgroups {0}, {0, 2} and
has subgroups {0}, {0, 2} and  . The factors are isomorphic to
. The factors are isomorphic to 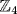 ,
, 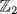 , {0} respectively, so these are the only possible images.
, {0} respectively, so these are the only possible images.
c. The normal subgroups of A4 are
![]()
and A4 (Exercise 19 §2.8). Thus the factor groups are isomorphic to A4, C3 (since  ) and {1}.
) and {1}.
35. If ϕ : G1 → G1/X is the coset map, we have β = ϕα : G → G1/X. This is onto because α and ϕ are both onto, and since
![]()
The isomorphism theorem completes the proof.
36.
a. It is closed because α + β is a homomorphism:
![]()
We have α + β = β + α because
![]()
Similarly, α + (β + γ) = (α + β) + γ. The unity is θ : X → Y where θ(x) = 0 for all x. Finally, the negative of α is −α : X → Y defined by (− α)(x) = − [α(x)] for all x.
c. For convenience, write  and
and  . Let d = gcd (m, n), and write e = nd. Given
. Let d = gcd (m, n), and write e = nd. Given  , define
, define 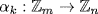 by
by
![]()
This is well defined:
![]()
This means 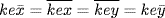 . So αk is well defined. We have
. So αk is well defined. We have
![]()
Hence  and we have a map
and we have a map
![]()
![]()
Hence we have αk+l = αk + αl; that is α(k + l) = α(k) + α(l).
α is onto. Let  , and write
, and write 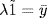 . Then
. Then
![]()
Thus  , so n
, so n  my. This gives nd
my. This gives nd  mdy. But nd and md are relatively prime, so nd
mdy. But nd and md are relatively prime, so nd  y, that is e
y, that is e  y, say y = ek. But then
y, say y = ek. But then
![]()
Thus λ = αk and α is onto.
We have ker α = {k  αk = 0}. But
αk = 0}. But

Hence  .
.
37.
a. The unity of Gω is [1) = (1, 1, 1, . . .). The inverse of [gi) is  . Finally
. Finally
![]()
Thus Gω is associative.
c. F → σGω is an isomorphism when σ(f) = [f(i)) = [f(0), f(1), f(2), . . .).
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
