8.1 Products and Factors
1. a. XY = {τ, τσ}{τ, τσ2} = {τ2, τ2σ2, τστ, τστσ2} = {ε, σ2, τ2σ2, τ2σ4} = {ε, σ2, σ} . YX = {τ, τσ2}{τ, τσ} = {τ2, τ2σ, τσ2τ, τσ2τσ} = {ε, σ, τ2σ, τ2σ2} = {ε, σ, σ2}.
3. If G′ ⊆ H, then H/G′  G/G′ because G/G′ is abelian. Hence H
G/G′ because G/G′ is abelian. Hence H  G by the correspondence theorem.
G by the correspondence theorem.
4.
a. G = D6 = {1, a, . . ., a5, b, ba, . . ., ba5}, o(a) = 6, o(b) = 2, aba = b. We have K = Z(D6) = {1, a3}. Write  ,
, 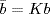 . Then
. Then 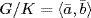 , 109
, 109 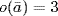 ,
,  ,
, 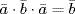 . Hence G/K ≅ D3 and the only subgroups of G/K are
. Hence G/K ≅ D3 and the only subgroups of G/K are 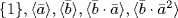 and G/K. So the subgroups of G containing K are G, K and
and G/K. So the subgroups of G containing K are G, K and

Note that H1 ≅ H2 ≅ H3 ≅ K4 —the Klein group (in contrast with (b)).
c. G = A4 and K = {ε, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)}. Then  , so
, so  is cyclic of order 3. Hence the only subgroups of A4 containing K are K and A4. In particular, K is maximal normal in A4.
is cyclic of order 3. Hence the only subgroups of A4 containing K are K and A4. In particular, K is maximal normal in A4.
5.
a. Every subgroup of  has the form
has the form  ,
, 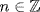 , and
, and  . This is simple (abelian) if and only if n is a prime. Thus
. This is simple (abelian) if and only if n is a prime. Thus  a prime} are the maximal normal subgroups of
a prime} are the maximal normal subgroups of  .
.
c. G = D10 = {1, a, . . ., a9, b, ba, . . ., ba9}, o(a) = 10, o(b) = 2, aba = b. If H is maximal normal in G, then G/H is abelian (it's order is ≤5) and so has order c, a prime dividing 20. Thus  so
so 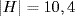 . The subgroups of order 10 are
. The subgroups of order 10 are
![]()
There is no element of order 4, so the subgroups of order 4 are

7. If K  G, G/K cyclic,
G, G/K cyclic,  ,
,  , let k
, let k  m and m
m and m  n. Then
n. Then  and
and  divides
divides 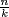 . Hence G/K cyclic implies it has a unique subgroup X with
. Hence G/K cyclic implies it has a unique subgroup X with 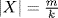 . Write X = H/K. Then
. Write X = H/K. Then  , so
, so 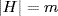 . If K ⊆ H1 ⊆ G and
. If K ⊆ H1 ⊆ G and  , then
, then 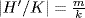 , so H′/K = H/K by the uniqueness. Thus H1 = H.
, so H′/K = H/K by the uniqueness. Thus H1 = H.
9. We must prove that (H1/K) ∩ (H2/K) = (H1 ∩ H2)/K. We have
![]()
by Lemma 2. If Kg  (H1/K) ∩ (H2/K), let Kg = Khi for hi
(H1/K) ∩ (H2/K), let Kg = Khi for hi  Hi, i = 1, 2 . Then g
Hi, i = 1, 2 . Then g  Khi ⊆ Hi for each i, so g
Khi ⊆ Hi for each i, so g  H1 ∩ H2. This shows that Kg
H1 ∩ H2. This shows that Kg  (H1 ∩ H2)/K, and so proves that
(H1 ∩ H2)/K, and so proves that
![]()
10. a. If HH1 = H1H, then  . Hence
. Hence 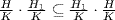 , and the other inclusion is similar. Conversely, if
, and the other inclusion is similar. Conversely, if  then
then  ; so
; so  because KH1 ⊆ H1. Thus HH1 ⊆ H1H and the other inclusion is similar.
because KH1 ⊆ H1. Thus HH1 ⊆ H1H and the other inclusion is similar.
11.  X∪ Y
X∪ Y  is a subgroup containing both X and Y, so
is a subgroup containing both X and Y, so  X
X ⊆
⊆  X ∪ Y
X ∪ Y  and
and  Y
Y ⊆
⊆  X ∪ Y
X ∪ Y  . Then
. Then  X
X
 Y
Y  ⊆
⊆  X ∪ Y
X ∪ Y  because
because  X∪ Y
X∪ Y  is closed. If
is closed. If  X
X
 Y
Y  =
=  X ∪ Y
X ∪ Y  , then
, then  X
X
 Y
Y  is a subgroup, so
is a subgroup, so  X
X
 Y
Y  =
=  Y
Y 
 X
X  Lemma 2 §2.8. Conversely, if
Lemma 2 §2.8. Conversely, if  X
X
 Y
Y  =
=  Y
Y 
 X
X  then
then  X
X
 Y
Y  is a subgroup (again by Lemma 2 §2.8). Since
is a subgroup (again by Lemma 2 §2.8). Since  X
X
 Y
Y  contains both X and Y, it contains X ∪ Y, and so
contains both X and Y, it contains X ∪ Y, and so  X∪ Y
X∪ Y  ⊆
⊆  X
X 
 Y
Y  by Theorem 8 §2.4.
by Theorem 8 §2.4.
12. a. H2 ⊆ H because H is closed; H ⊆ H2 because 1  H.
H.
13. Write 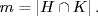 Since H ∩ K is a subgroup of H we have m
Since H ∩ K is a subgroup of H we have m  {1, p, q, pq} by Lagrange's theorem. Similarly m
{1, p, q, pq} by Lagrange's theorem. Similarly m  {1, q, r, qr}, so m
{1, q, r, qr}, so m  {1, q} . But if m = 1 then
{1, q} . But if m = 1 then  a contradiction. So m = q as required.
a contradiction. So m = q as required.
15. Note that KA and KB are subgroups by Theorem 5 §2.8, and KA = AK, KB = BK. If kb  KB, we have Ab = bA and Kb = bK. Hence
KB, we have Ab = bA and Kb = bK. Hence
![]()
Thus KA  KB.
KB.
17. Given K  G,
G,  , assume H is any subgroup of G with
, assume H is any subgroup of G with  . Then HK is a subgroup and HKK ≅ HH ∩ K by the second isomorphism theorem. Since
. Then HK is a subgroup and HKK ≅ HH ∩ K by the second isomorphism theorem. Since  , we have
, we have  for some k such that 0 ≤ k ≤ n. Hence
for some k such that 0 ≤ k ≤ n. Hence  . But HKK is a subgroup of GK, and
. But HKK is a subgroup of GK, and  . It follows that pk divides m Since p
. It follows that pk divides m Since p m by hypothesis, we have k = 0. Thus H = H ∩ K and HK = K; so certainly K ⊆ H. Hence H = K because
m by hypothesis, we have k = 0. Thus H = H ∩ K and HK = K; so certainly K ⊆ H. Hence H = K because 
18.
a. We have M ⊂ KM because M = KM implies K ⊆ M. Since KM is normal, we have M = KM because M is maximal normal.
c. By (a) and Theorem 3,  so (c) follows from (b).
so (c) follows from (b).
19. a. The argument in Example 3 goes through with “cyclic” replaced by “abelian”. All that is needed is that subgroups and factor groups of abelian groups are again abelian. However, we give a slick argument using (b) below. Let G′ be metabelian, that is G′ is abelian by (b). If H is a subgroup of G, then H′ ⊆ G′ (since commutators in H are commutators in G), so H′ is abelian. Thus H is metabelian. Now suppose that N  G. Then in GN, each commutator [Na, Nb] = N[a, b]
G. Then in GN, each commutator [Na, Nb] = N[a, b]  NG′. Hence
NG′. Hence  Since
Since 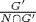 is abelian (being a factor group of the abelian group G′), it follows that
is abelian (being a factor group of the abelian group G′), it follows that  is abelian, that is
is abelian, that is  is metabelian.
is metabelian.
21. We are given subgroups H and K where 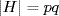 ,
,  , p ≠ q primes. Since H ∩ K ⊆ K and
, p ≠ q primes. Since H ∩ K ⊆ K and 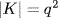 , we have
, we have 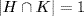 , q or q2 by Lagrange's theorem. Similarly H ∩ K ⊆ H and
, q or q2 by Lagrange's theorem. Similarly H ∩ K ⊆ H and  shows that
shows that 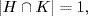 p, q or pq. Hence
p, q or pq. Hence 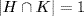 or q, and it remains to show
or q, and it remains to show 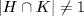 . But
. But 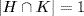 gives (by Theorem 4)
gives (by Theorem 4) 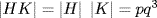 . Since HK ⊆ G, this contradicts
. Since HK ⊆ G, this contradicts  .
.
22. a. Let a ≠ b be elements of order 2. Since G is abelian, H = {1, a, b, ab} is closed, and so is a subgroup. Then  divides
divides 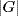 by Lagrange's theorem.
by Lagrange's theorem.
23. The unity of M is {1} = 1. So if X is a unit in M, let XY = 1. This means that xy = 1 for all x  X, y
X, y  Y. So, given y
Y. So, given y  Y, x = y−1 for all x
Y, x = y−1 for all x  X. Thus X is a singleton, say X = {g} = g
X. Thus X is a singleton, say X = {g} = g  G. Conversely, each g
G. Conversely, each g  G is a unit in M because gg−1 = 1.
G is a unit in M because gg−1 = 1.
24.
a. We must show 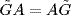 . If σ
. If σ  A = aut G and
A = aut G and  (τa(g) = ag for all g
(τa(g) = ag for all g  G), then στa(g) = σ(ag) = σ(a) · σ(g) = τσ(a)σ(g). Thus στa = τσ(a)σ, so
G), then στa(g) = σ(ag) = σ(a) · σ(g) = τσ(a)σ(g). Thus στa = τσ(a)σ, so 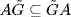 . If we take b = σ(a), this is
. If we take b = σ(a), this is 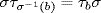 , so
, so  .
.
c. Let  and
and  , say λ = τbσ. Then (using τaσ = στσ(a) in (a)):
, say λ = τbσ. Then (using τaσ = στσ(a) in (a)):
![]()
Thus  .
.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
