2.1 Binary Operations
1.
a. This is not commutative: 1 ∗ 2 = − 1 while 2 ∗ 1 = 1. It is not associative: (2 ∗ 1) ∗ 3 = 1 ∗ 3 = − 2, while 2 ∗ (1 ∗ 3) = 2 ∗ (− 2) = 4. There is no unity: If e ∗ a = a for all a, then e − a = a so e = 2a for all a. This is impossible.
c. This is commutative: a ∗ b = a + b − ab = b + a − ba = b ∗ a. It is associative:
![]()
and, similarly, this equals (a ∗ b) ∗ c. The unity is 0:
![]()
Every a ≠ 1 has an inverse
![]()
e. This is not commutative (p, q) ∗ (p′, q′) = (p, q′) while (p′, q′) ∗ (p, q) = (p′, q) . It is associative:
![]()
There is no unity: If (a, b) ∗ (p, q) = (p, q) for all p, q, then a = p for all p.
g. This is commutative: gcd (n, m) = gcd (m, n). It is associative: Write d = gcd (k, m), d′ = gcd (m, n). Then d1 = (k ∗ m) ∗ n = gcd (d, n), so d1  d and d1
d and d1  n. But then, d1
n. But then, d1  k, d1
k, d1  m and d1
m and d1  n. It follows that d1
n. It follows that d1  k and d1
k and d1  d′, so d1
d′, so d1  gcd (k, d′) = k ∗ (m ∗ n). A similar argument shows k ∗ (m ∗ n)
gcd (k, d′) = k ∗ (m ∗ n). A similar argument shows k ∗ (m ∗ n)  (k ∗ m) ∗ n, so these are equal. Finally, there is no unity: If e ∗ n = n for all n, then n = gcd (e, n) so n
(k ∗ m) ∗ n, so these are equal. Finally, there is no unity: If e ∗ n = n for all n, then n = gcd (e, n) so n  e for all n. This is impossible.
e for all n. This is impossible.
i. If we write 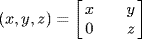 as a matrix, this operation is matrix multiplication, and so is associative. It is not commutative
as a matrix, this operation is matrix multiplication, and so is associative. It is not commutative  while
while  . The unity is the identity matrix
. The unity is the identity matrix  , and
, and 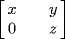 has an inverse if and only if x ≠ 0 and z ≠ 0. The inverse then is
has an inverse if and only if x ≠ 0 and z ≠ 0. The inverse then is 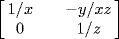 .
.
2.
a. 1(yz) = yz = (1y)z; x(1z) = xz = (x1)z; and x(y1) = xy = (xy)1.
c. M is clearly closed and 1 is the unity. M is associative by (a).
3.
a. We have ab = b, b2 = a. Hence a2 = ab2 = (ab)b = b2 = a, and hence ba = bb2 = b2b = ab = b. Hence a is the unity and the operation is associative by Exercise 2.
5. This is associative:
![]()
Clearly this equals [(a1  an) · (b1
an) · (b1  bm)] · c1
bm)] · c1  ck. The unity is the empty word λ (with no letters). It is not commutative if
ck. The unity is the empty word λ (with no letters). It is not commutative if  : a · b ≠ b · a if a ≠ b. Note that if A = {a}, then W = {1, a, aa, aaa, . . . } is commutative. If
: a · b ≠ b · a if a ≠ b. Note that if A = {a}, then W = {1, a, aa, aaa, . . . } is commutative. If  words, it is clear that
words, it is clear that  . So λ is the only unit.
. So λ is the only unit.
7. It is associative:
![]()
and this equals [(m, n)(m′n′)](m′′, n′′). The unity is (1, 1) . M × N is commutative if and only if M and N are both commutative. Finally, (m, n) is a unit if and only if m and n are units in M and N respectively, then (m, n)−1 = (m−1, n−1).
8.
a. Given am = am+n, we have am = aman = am+nan = am+2n. Continue to get am = am+kn for all k ≥ 0. Then multiply by ar to get am+r = am+kn+r for all r ≥ 0. Hence am+r is an idempotent if r ≥ 0 and k ≥ 0 satisfy 2(m + r) = m + kn + r, that is m + r = kn. So choose k ≥ 0 such that kn ≥ m; and then take r = kn − m. One choice: k = m, r = m(n − 1). Then m + r = m + m(n − 1), so amn is an idempotent.
9. a. a24a = a25 = (a5)5 = (b5)5 = b25 = b24b = a24b. Cancel a24 by cancelling a 24 times.
11. Let e ≠ f be left unities (ex = x = fx for all x). If g is a right unity (xg = x), then g = eg = e and g = fg = f, so e = f, contrary to hypothesis.
12. a. If au = bu, then (au)u−1 = (bu)u−1, that is a(uu−1) = b(uu−1) ; a1 = b1 ; a = b.
13. Let  . Then u(vw) = 1, and we claim that (vw)u = 1 too (so u is a unit). In fact
. Then u(vw) = 1, and we claim that (vw)u = 1 too (so u is a unit). In fact  , so (vw)u = 1 by hypothesis. Thus u−1 exists. But then
, so (vw)u = 1 by hypothesis. Thus u−1 exists. But then  is a unit by Theorem 5 (since u and uv are both units.)
is a unit by Theorem 5 (since u and uv are both units.)
15. a. If σ is a bijection, let  for some
for some  (σ is onto). This means 1 = uv. But σ(vu) = u(vu) = (uv)u = u = σ1, so vu = 1 because σ is one-to-one.
(σ is onto). This means 1 = uv. But σ(vu) = u(vu) = (uv)u = u = σ1, so vu = 1 because σ is one-to-one.
Conversely, let u be a unit. If σa = σb, then ua = ub, so a = u−1ua = u−1ub = b. This shows σ is one-to-one. If b  M, then b = u(u−1b) = σ(u−1b), so σ is onto. Thus σ is a bijection.
M, then b = u(u−1b) = σ(u−1b), so σ is onto. Thus σ is a bijection.
17.
a. If 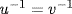 , then
, then  by Theorems 4 and 5.
by Theorems 4 and 5.
c. Use (b) twice: uv = vu gives  , so (since
, so (since  is a unit)
is a unit)  , as required. Alternatively, if uv = vu then (uv)−1 = (vu)−1 by Theorem 4, whence
, as required. Alternatively, if uv = vu then (uv)−1 = (vu)−1 by Theorem 4, whence 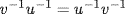 by Theorem 5.
by Theorem 5.
18. (1) ⇒ (2). If ab = 1 then a−1 exists by (1) so b = 1b = a−1ab = a−1. Hence b is a unit by Theorem 5.
19. Let M = {a1, a2, . . ., an}, and consider X = {a1u, a2u, . . ., anu}. If aiu = aju, then ai = aiuv = aj, so i = j. Thus |X| = n = |M|, so since X ⊆ M we have X = M. In particular 1  X , say 1 = wu,
X , say 1 = wu,  . Then
. Then
![]()
so 1 = wu = vu. This means  is an inverse of u.
is an inverse of u.
20.
a. a  a for all a because a = a · 1; if a
a for all a because a = a · 1; if a  b, then a = bu, so b = au−1, that is b
b, then a = bu, so b = au−1, that is b  a. If a
a. If a  b and b
b and b  c, let a = bu, b = cv,
c, let a = bu, b = cv,  units. Then a = (cv)u = c(vu), and so a
units. Then a = (cv)u = c(vu), and so a  c because vu is a unit. Note that M need not be commutative here.
c because vu is a unit. Note that M need not be commutative here.
c. M is associative because  . Since 1 is the unity of M, we obtain
. Since 1 is the unity of M, we obtain  ; and similarly,
; and similarly,  . Hence
. Hence  is the unity of
is the unity of  Next
Next  so M is commutative. Finally, if
so M is commutative. Finally, if  is a unit in M, let
is a unit in M, let 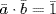 . Then ab
. Then ab  1 so 1 = abu. Thus a is a unit in M, so a
1 so 1 = abu. Thus a is a unit in M, so a  1. Hence
1. Hence 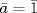 , as required.
, as required.
21.
a. E(M) is closed under composition since, if α, β  E(M), then
E(M), then
![]()
for all x, y  M. We have 1M(xy) = xy = 1Mx · y, so 1M
M. We have 1M(xy) = xy = 1Mx · y, so 1M  E(M) and 1M is the unity of E(M). Finally, composition is always associative, so E(M) is a monoid.
E(M) and 1M is the unity of E(M). Finally, composition is always associative, so E(M) is a monoid.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
