6.1 Vector Spaces
1.
a. No. 0∉ U.
c. No. 0 ∉ U and not closed under addition.
2.
a. Yes. This is because (2f)(x) = 2f(x) and (f + g)(x) = f(x) + g(x) for all f, g  F[x].
F[x].
c. No. 0 ∉ U.
3. 
4.
a. The inclusion ⊇ is clear. Since
![]()
and similarly for  and
and  , 89 we have also proved the inclusion ⊆.
, 89 we have also proved the inclusion ⊆.
5. We have  , so adding −(av) to both sides gives
, so adding −(av) to both sides gives 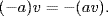 Similarly
Similarly 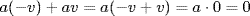 yields
yields 
7.
a. Dependent. (1, 2, 3) + 2(4, 0, 1) + 3(2, 1, 0) = (0, 0, 0).
c. Independent. a(x2 + 1) + b(x + 1) + cx = 0 gives a = 0, b + c = 0, a + b = 0; so a = b = c = 0.
9.
a. If  then
then  ;
;  . Thus 2ab = 0 and a2 + 2b2 = 3c2. If a = 0, b ≠ 0 then
. Thus 2ab = 0 and a2 + 2b2 = 3c2. If a = 0, b ≠ 0 then  , a contradiction. If a ≠ 0, b = 0 then
, a contradiction. If a ≠ 0, b = 0 then  , a contradiction. So a = b = 0 = c.
, a contradiction. So a = b = 0 = c.
11. {(1, − 1, 0), (1, 1, 1), (a, 0, 0)}; a ≠ 0 in 
13. If rf + sg = 0 then rf(a) + sg(a) = 0 so s = 0; and rf(b) + sg(b) = 0 implies that a = 0.
15. Since dim M2(F) = 4, the matrices I, A, A2, A3, A4 cannot be independent by the fundamental theorem. The result follows.
17. If Mn(F) = span{A1, . . ., Ak} then  , ai
, ai  F. Then for all
F. Then for all
V Mn(F)
Mn(F)  , a contradiction.
, a contradiction.
V
19.
a. {1, r, . . ., rn} is not independent because dim F R = n. So
![]()
for some ai not all zero. Thus p(r) = 0 when  in F[x].
in F[x].
21. Clearly each of  so it follows that span
so it follows that span span
span . If a1 ≠ 0 the other inclusion follows by the same argument because
. If a1 ≠ 0 the other inclusion follows by the same argument because  .
.
22.
a. If {u1, . . ., um} ⊆ {u1, . . ., um, . . ., un} —independent, then  implies
implies  where am+1 =
where am+1 =  = an = 0. So ai = 0 for all i by the independence of {u1, . . ., um, . . ., un}.
= an = 0. So ai = 0 for all i by the independence of {u1, . . ., um, . . ., un}.
23.
a. Given such a set  , let
, let  . Then
. Then  implies
implies 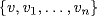 is independent (Lemma 1), contrary to the choice of the
is independent (Lemma 1), contrary to the choice of the 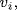 so
so  for all
for all  ; that is
; that is 
25. If  then
then  , so
, so
 is dependent. If it is dependent, then
is dependent. If it is dependent, then  , ai not all
, ai not all
0. If ak ≠ 0 then
0. If ak ≠ 0 then
26.
a. Clear by the subspace test.
c. Pick a basis {x1, . . ., xk} of U ∩ V. By Theorem 8, extend to a basis {x1, . . ., xk, u1, . . ., um} of U and a basis 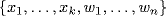 of W. It suffices to prove the following Claim.
of W. It suffices to prove the following Claim.
Claim: is a basis of U + W. It clearly spans. If
is a basis of U + W. It clearly spans. If
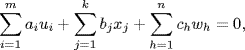
write 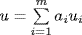 ,
,  and
and 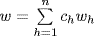 ; it suffices to prove
; it suffices to prove  . We have
. We have 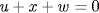 so
so 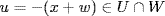 . Thus
. Thus  that is
that is  . Since {ui, xj} is linearly independent, this forces u = 0. Then
. Since {ui, xj} is linearly independent, this forces u = 0. Then  so, similarly,
so, similarly, 
27. If U = span{ui} and 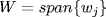 then
then 
28.
a. They are clearly subspaces. For example p, q even means
![]()
If p(x) U ∩ W then p(x) = − p(− x) = − p(x), so p(x) = 0 (because 2 ≠ 0 in F). Thus U ∩ W = 0. If f(x) V then f(x) = p(x) + q(x) where
![]()
and  . So V = U + W.
. So V = U + W.
29. W is clearly a subspace. Let {u1, . . ., um} be a basis of U.
Case 1.  . Then W = U so dim U = m.
. Then W = U so dim U = m.
Case 2.  . Then
. Then  is independent (Lemma 1) and is clearly a basis of W (definition of W). So dim W = m + 1.
is independent (Lemma 1) and is clearly a basis of W (definition of W). So dim W = m + 1.
31.
a. They are additive subgroups by group theory. If 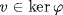 then
then  for all a F. If
for all a F. If 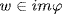 , say
, say  , then
, then
![]()
c. Let {u1, . . ., um} be a basis of ker ϕ; extend to a basis  of V. It suffices to show that
of V. It suffices to show that  is a basis of imϕ.
is a basis of imϕ.
Span. If  ϕ and
ϕ and  then
then

Independent. If 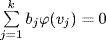 then
then  , so
, so

Thus  , so bj = 0 for all j.
, so bj = 0 for all j.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
