2.6 Cosets and Lagrange's Theorem
1.
a. 1H = H1 = {1, a4, a8, a12, a16} aH = Ha = {a, a5, a9, a13, a17} a2H = Ha2 = {a2, a6, a10, a14, a18} a3H = Ha3 = {a3, a7, a11, a15, a19} 1K = K1 = {1, a2, a4, a6, a8, a10, a12, a14, a16, a18} aK = Ka = {a, a3, a5, a7, a9, a11, a13, a15, a17, a19}
c. 

e. 

3. No. If H = {1, b} ⊆ D3, then Ha = {a, ba) = Hba, but aH = {a, ba2} ≠ baH.
5. a. a ≡ a because a−1a = 1  H. If a ≡ b then b−1a
H. If a ≡ b then b−1a  H, whence a−1b = (b−1a)−1
H, whence a−1b = (b−1a)−1  H, so b ≡ a. Finally, if a ≡ b and b ≡ c then b−1a
H, so b ≡ a. Finally, if a ≡ b and b ≡ c then b−1a  H and c−1b
H and c−1b  H, so c−1a = (c−1b)(b−1a)
H, so c−1a = (c−1b)(b−1a)  H. Thus a ≡ c.
H. Thus a ≡ c.
7. If Ha = bH, then a  Ha gives a
Ha gives a  bH, so aH = bH. Thus aH = Ha. Similarly bH = Hb, so aH = Ha = bH = Hb.
bH, so aH = bH. Thus aH = Ha. Similarly bH = Hb, so aH = Ha = bH = Hb.
9.
a. If 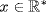 , then
, then 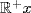 equals
equals  or
or 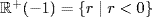 , according as x > 0 or x < 0. Here
, according as x > 0 or x < 0. Here 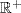 is the set of positive real numbers, and
is the set of positive real numbers, and  is the set of negative real numbers.
is the set of negative real numbers.
c. If  , write x = n + t,
, write x = n + t,  , 0 ≤ t < 1. Then
, 0 ≤ t < 1. Then 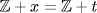 consists of all points on the line at distance t to the right of an integer.
consists of all points on the line at distance t to the right of an integer.
10. a. Write H = a6
a6  . Then
. Then 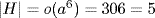 , so
, so  .
.
11. a. (H ∩ K)a ⊆ Ha ∩ Ka is clear. If x  Ha ∩ Ka, write x = ha = ka, h
Ha ∩ Ka, write x = ha = ka, h  H, k
H, k  K. Then h = k by cancellation, so h
K. Then h = k by cancellation, so h  H ∩ K. Thus x = ha
H ∩ K. Thus x = ha  (H ∩ K)a.
(H ∩ K)a.
12.
a. If o(g) = m, we show m = 12. We have m  12 by Lagrange's theorem, so m is one of 1, 2, 3, 4, 6 or 12. If m ≠ 12, then m|4 or m|6, so g4 = 1 or g6 = 1, contrary to hypothesis.
12 by Lagrange's theorem, so m is one of 1, 2, 3, 4, 6 or 12. If m ≠ 12, then m|4 or m|6, so g4 = 1 or g6 = 1, contrary to hypothesis.
c. Now o(g) divides 60, so is one of 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60. Again each of these except 60 divides one of 12, 20 or 30, so o(g) = 60.
13. If  , then m|12 and 4|m (because K ⊆ H). Thus
, then m|12 and 4|m (because K ⊆ H). Thus  or
or 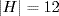 ; that is H = K or H = A4.
; that is H = K or H = A4.
5. Since H ∩ K ⊆ H, we have that 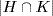 divides the prime
divides the prime 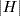 . So either
. So either  (and H ∩ K = {1}) or
(and H ∩ K = {1}) or  (so H ∩ K = H, that is H ⊆ K).
(so H ∩ K = H, that is H ⊆ K).
1. a. We have gn = 1 by Lagrange's theorem. Since gcd (m, n) = 1, write 1 = xn + ym;  . If gm = 1, then g = g1 = (gm)x(gn)y = 1x1y = 1.
. If gm = 1, then g = g1 = (gm)x(gn)y = 1x1y = 1.
17. Let H be a subgroup of G, H ≠ G. Then 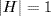 or p by Lagrange's Theorem. If
or p by Lagrange's Theorem. If 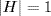 , then H =
, then H = 1
1  . If
. If 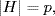 then H is cyclic by Corollary 3 of Lagrange's Theorem.
then H is cyclic by Corollary 3 of Lagrange's Theorem.
19. If x = ak = bk, then x
 a
a  ∩
∩  b
b  . But
. But  a
a  ∩
∩  b
b  = {1} by Corollary 4 of Lagrange's Theorem because
= {1} by Corollary 4 of Lagrange's Theorem because  and
and 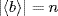 are relatively prime. Thus ak = 1 and bk = 1, so m
are relatively prime. Thus ak = 1 and bk = 1, so m  k and n
k and n  k. Thus mn
k. Thus mn  k, again because m and n are relatively prime.
k, again because m and n are relatively prime.
21. If n = 1 then  . If n ≥ 2 and
. If n ≥ 2 and  , then k = qn + r, 0 ≤ r ≤ n − 1, so
, then k = qn + r, 0 ≤ r ≤ n − 1, so  . Thus
. Thus  ; that is the cosets are
; that is the cosets are
![]()
These are distinct. For if  with 0 ≤ r ≤ s ≤ n − 1 then
with 0 ≤ r ≤ s ≤ n − 1 then  , so 0 ≤ s − r ≤ s ≤ n − 1. But s − r ≥ 0 is a multiple of n; so s − r = 0. Thus there are exactly n cosets.
, so 0 ≤ s − r ≤ s ≤ n − 1. But s − r ≥ 0 is a multiple of n; so s − r = 0. Thus there are exactly n cosets.
23. Let g  G, g ≠ 1. Then o(g) divides
G, g ≠ 1. Then o(g) divides  , say o(g) = pm, m ≤ k. Since m ≠ 0,
, say o(g) = pm, m ≤ k. Since m ≠ 0,  by Theorem 5 §2.4.
by Theorem 5 §2.4.
25. a. For k ≥ 1 we induct on k. It is given for k = 1 . If akbak = b for some k ≥ 0, then ak+1bak+1 = aba = a. Thus akbak = b for all k ≥ 1 by induction. It is clear if k = 0 . But a−1ba−1 = a−1(aba)a−1 = b, and a similar argument shows a−kba−k = b if k ≥ 1.
27. No. D5 × C3 has no element of order 10, while D3 × C5 has 12 elements of order 10.
29. a. H ∩ K is a subgroup of H so H ∩ K = {1} or H ∩ K = H by Lagrange's Theorem. Similarly, H ∩ K ⊆ K implies that H ∩ K = {1} or H ∩ K = K. Thus H ∩ K ≠ {1} implies H = H ∩ K = K.
31. If 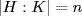 , let Kh1, . . ., Khn be the distinct cosets of K in H. Thus H = Kh1 ∪
, let Kh1, . . ., Khn be the distinct cosets of K in H. Thus H = Kh1 ∪  ∪ Khn, a disjoint union. Then Hg ⊆ Kh1g ∪
∪ Khn, a disjoint union. Then Hg ⊆ Kh1g ∪ ∪Khng is clear, and it is equality because K ⊆ H. Thus each H-coset in G is the union of nK-cosets. If
∪Khng is clear, and it is equality because K ⊆ H. Thus each H-coset in G is the union of nK-cosets. If  this gives
this gives 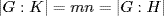
 . Conversely, if
. Conversely, if 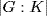 is finite, then
is finite, then  is clearly finite and
is clearly finite and  is finite by the hint since each H-coset is a union of K -cosets.
is finite by the hint since each H-coset is a union of K -cosets.
32. a. (H ∩ K)g ⊆ Hg ∩ Kg is clear. If x  Hg ∩ Kg, write x = hg = kg, h
Hg ∩ Kg, write x = hg = kg, h  H, k
H, k  K. Then h = k
K. Then h = k  H ∩ K by cancellation, so x = hg
H ∩ K by cancellation, so x = hg  (H ∩ K)g. Hence (H ∩ K)g = Hg ∩ Kg, so each (H ∩ K)g coset is the intersection of one of the mH-cosets with one of the nK-cosets. There are thus at most mnH ∩ K-cosets.
(H ∩ K)g. Hence (H ∩ K)g = Hg ∩ Kg, so each (H ∩ K)g coset is the intersection of one of the mH-cosets with one of the nK-cosets. There are thus at most mnH ∩ K-cosets.
33. If H1,  , Hn are all of finite index in G, we show H1 ∩
, Hn are all of finite index in G, we show H1 ∩  ∩ Hk is of finite index for each k = 1, 2, . . ., n. This is clear if k = 1. If it holds for some k, then H1 ∩
∩ Hk is of finite index for each k = 1, 2, . . ., n. This is clear if k = 1. If it holds for some k, then H1 ∩  ∩ Hk+1 = (H1 ∩
∩ Hk+1 = (H1 ∩  ∩ Hk) ∩ Hk+1 is a finite index by part (a) of the preceding exercise.
∩ Hk) ∩ Hk+1 is a finite index by part (a) of the preceding exercise.
35. a. a ≡ a for all a because a = 1a1. If a ≡ b, then a = hbk, h  H, k
H, k  K, so b = h−1ak−1, that is b ≡ a. If a ≡ b and b ≡ c, then a = hbk, b = h1ck1, so a = (hh1)c(kk1). Thus a ≡ c.
K, so b = h−1ak−1, that is b ≡ a. If a ≡ b and b ≡ c, then a = hbk, b = h1ck1, so a = (hh1)c(kk1). Thus a ≡ c.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
