4.2 Factorization of Polynomials over a Field
1. a. f = a(a−1f).
2. a. Yes, since a ≠ 0, f(b) = 0if and only if af(b) = 0.
3. a. f(1) = 0; indeed f = (x − 1)(x2 − x + 2) over any field.
4.
a. Irreducible because it has no roots in 
c. 
in 
. Not irreducible.
in . Not irreducible.
e. Irreducible, because it has no root in 
5.
∗Every polynomial of odd degree in 
has a root in 
–see Exercise 9.
has a root in –see Exercise 9.
7. f = [x − (1 − i)][x − (1 + i)][x − i][x + i] = (x2 − 2x + 2)(x2 + 1) = x4 − 2x3 + 3x2 − 2x + 2.
The polynomial f2 has the same roots, albeit of different multiplicities.
8. a. As f is monic, we may assume that both factors are monic (Exercise 6). Hence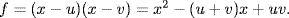 
Now equate coefficients.
Now equate coefficients.
9. Assume f = anxn + an−1xn−1 + 
+ a0, an ≠ 0, n odd. Then 
is monic and has the same roots as f. So assume
+ a0, an ≠ 0, n odd. Then 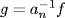is monic and has the same roots as f. So assume
If x ≠ 0 then
Thus lim x→∞f(x) =∞ and (because n is odd) lim x→−∞f(x) =− ∞. Thus there exist a > 0 and b < 0 such that f(a) > 0 and f(b) < 0. But then the intermediate value theorem of calculus gives c between a and b such that f(c) = 0.
11. If f is irreducible, then 0 is not a root so f(0) ≠ 0 is the constant term. Hence f has the form f = 1 + xn1 + xn2 + + xnk. Then 0 ≠ f(1) = k + 1 = the number of terms in f. Thus k + 1 is odd. The converse is false: x4 + x2 + 1 passes the test, but x4 + x2 + 1 = (x2 + x + 1)2 in 
+ xnk. Then 0 ≠ f(1) = k + 1 = the number of terms in f. Thus k + 1 is odd. The converse is false: x4 + x2 + 1 passes the test, but x4 + x2 + 1 = (x2 + x + 1)2 in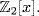
13. If p satisfies (1) and (2), it has no linear factor by (1). If p fails to be irreducible it must factor as a quadratic and a cubic. Both are irreducible (by (1)), so by Example 5 and Exercise 10, either p = (x2 + x + 1)(x3 + x + 1) = x5 + x4 + 1 or p = (x2 + x + 1)(x3 + x2 + 1) = x5 + x + 1. These are ruled out by (2). Conversely, if p is irreducible then (1) comes from Theorem 1 and (2) from the above factorizations of x5 + x4 + 1 and x5 + x + 1.
15. As in Exercise 1, this holds if the list is the set of all products of two (possibly equal) irreducible quadratics. By Exercise 14, they are
17. If p6 ≡ 3 (mod 4), the only other possibility is p ≡ 1 (mod4) . But then x2 + 1 has a root in 
by the Corollary to Theorem 8 §1.3. This shows that x2 + 1 is not irreducible.
by the Corollary to Theorem 8 §1.3. This shows that x2 + 1 is not irreducible.
18.
a. 3x4 + 2 = 3(x − 1)(x + 1)(x − 3)(x + 3) in 
c. x3 + 2x2 + 2x + 1 = (x + 1)(x + 3)(x + 5) in 
e. x4 − x2 + x − 1 = (x − 1)(x − 2)(x2 + 3x + 6) in 
19. x5 + x4 + 1 = (x2 + x + 1)(x3 + x + 1) in 
20. x5 + x2 − x + 1 = (x2 + 1)(x3 − x + 1) in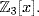 
21.
a. The possible rational roots are ± 1, ±2, 
, 
. Direct checking shows none is a root, so it is irreducible by Theorem 1. Alternatively, modulo 5 the polynomial is 3x3 + x + 2 = 3(x3 + 2x − 1) and this has no root in 
, again by a direct check.
, . Direct checking shows none is a root, so it is irreducible by Theorem 1. Alternatively, modulo 5 the polynomial is 3x3 + x + 2 = 3(x3 + 2x − 1) and this has no root in , again by a direct check.
c. Possible rational roots ±1, ±2, ±3, ±6. None work. Alternatively, modulo 5 it is x3 − x2 + x + 1, and this has no roots in 
22. a. The Eisenstein criterion applies with p = 3.
23.
a. f(x + 1) = x4 + 4x3 + 6x2 + 6x + 2, so the Eisenstein criterion applies with p = 2.
c. f(x + 1) = x4 + 4x3 + 6x2 + 4x + m + 1. Since m + 1 = 4k − 2 = 2(2k − 1) the Eisenstein criterion applies with p = 2.
24. f(x − 1) = (x − 1)4 + 4(x − 1)3 + 4(x − 1)2 + 4(x − 1) + 5 = x4 − 2x2 + 4x + 2 . Use Eisenstein with p = 2.
25. (1 + x)f = 1 + xp. Replace x by x − 1:
Then f(x − 1) = xp−1 − pp − 1xp−2 + − p2x + p. This is irreducible over 
by Eisenstein (with p), so f is also irreducible.
− p2x + p. This is irreducible over by Eisenstein (with p), so f is also irreducible.
26.
a. f4(x) = x3+ x2 + x + 1 = (x + 1)(x2 + 1);
f6(x) = x5 + x4 + x3 + x2 + x + 1 = (x + 1)(x2 + x + 1)(x2 − x + 1).
27. If f = xp + p2mx + (p − 1) then
The Eisenstein criterion (using p) applies here because p does not divide pm + 1.
29. The Eisenstein criterion applies using the prime p.
31. If f is irreducible in K[x] it cannot factor properly in F[x] because F[x] ⊆ K[x].
33. We are done by Theorem 1 as 1, 2, 3, and 7 are roots of x2 + x + 1 in 
for p = 3, 7, 13 and 19 respectively, and x2 + x + 1 has no roots in 
for p = 2, 5, 11 and 17.
for p = 3, 7, 13 and 19 respectively, and x2 + x + 1 has no roots in 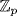for p = 2, 5, 11 and 17.
34. Take m = 7q where q is any prime except 7. Then the Eisenstein criterion (with p = 7) shows that f is irreducible over 
35.
a. f has no rational roots. If f = (x2 + ax + b)(x2 + cx + d), comparing coefficients gives a + c = 3, b + ac + d = 1, ad + bc = 3, bd = 1. Thus b = d = ± 1, c = 3 − a, so 3 = b(a + c) = 3b, (b = 1). Then b + ac + d = 1 gives 2 + a(3 − a) = 1, so a2 − 3a − 1 = a. This has no integer roots, so f is already irreducible.
c. f has no rational roots (the candidates are ±1, ±2). Suppose f = (x2 + ax + b)(x2 + cx + d). Then, as in (a)
Thus (b, d) = (1, − 2), (− 1, 2), (2, − 1) or (− 2, 1). By symmetry we consider only (1, − 2) and (− 1, 2).
Case 1. (b, d) = (1, − 2). Then
no root in 
Case 2. (b, d) = (− 1, 2). Now
so a = 3, c = − 1. The factorization is f = (x2 + 3x − 1)(x2 − x + 2). Both these quadratics are irreducible (no root in 
so this is the desired factorization.
so this is the desired factorization.
a. Not irreducible. x5 + x + 1 = (x2 + x + 1)(x3 − x2 + 1). The factors are irreducible (no roots in 
37. Not irreducible. x5 + x + 1 = (x2 + x + 1)(x3 − x2 + 1). The factors are irreducible (no roots in 
39.
a. g = (x + 4)f + (4x + 3) and f = (4x + 2)(4x + 3) + 1. Hence
c. g = (x3 + x2 − x − 1)f + (4x − 8) and 
Hence
Hence
41. If f = gcd (f, g) then f|g is clear. Conversely, if g = qf, let d = gcd (f, g). Write d = hf + kg with h, k in F[x]. Then d = hf + kqf, so f|d. But also d|f so d = f by Theorem 9 because d and f are both monic.
42. Let 1 = mf + kg with m and k in F[x].
a. If h = pf and h = qg, then
43.
a. Define σ and τ : F[x] → F[x] by σ(f) = f(x + b) and τ(f) = f(x − b). Then στ = 1F[x] and τσ = 1F[x] so σ (and τ) is a bijection. Observe that σ(f + g) = f(x + b) + g(x + b) = σ(f) + σ(g), when we use the evaluation theorem for F[x]. Similarly, σ(fg) = σ(f) · σ(g) so σ is a automorphism (and τ = σ−1).
c. Let σ : F[x] → F[x] be an automorphism such that σ(a) = a for all a 
F. Put σ(x) = p. If 
, then
F. Put σ(x) = p. If 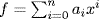, then
Now write σ−1(x) = q so σ−1(f) = f(q) for all f in F[x]. Hence x = σ[σ−1(x)] = σ(q) = p(q). Now p ≠ 0 because σ is one-to-one, and similarly q ≠ 0. If °p = m and °q = n then 1 = °x = °{p(q)} = mn. It follows that m = n = 1 so p = ax + b, a ≠ 0. Thus σ(f) = f(ax + b) for all f in F[x], as required.
44. This was done in Exercise 37 §4.1.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.