1.3 Integers Modulo n
1.
a. True. 40−13=3·9
c. True. −29−6=(−5)7
e. True. 8−8=0·n for any n.
g. False. 84≡(64)2≡(−1)2≡1 (mod13).
2.
a. 2k−4=7q, so q is even. Thus k=2+7x for some integer x; that is k≡2 (mod 7).
c 2k≡0 (mod 9), so 2k=9q. Thus 2  q, so k=9x for some integer x; that is k≡0 (mod 9).
q, so k=9x for some integer x; that is k≡0 (mod 9).
3.
a. 10≡0 (mod k), so k  10: k=2, 5, 10.
10: k=2, 5, 10.
c. k2−3=qk, so k  3. Thus k=1, 3 so, (as k≥2 by assumption) k=3.
3. Thus k=1, 3 so, (as k≥2 by assumption) k=3.
5.
a. a≡b (mod 0) means a−b=q·0 for some q, that is a=b.
6.
a. a≡a for all a because n  (a−a). Hence if n
(a−a). Hence if n  (a−b), then n
(a−b), then n  (b−a). Hence if a−b=xn and b−c=yn,
(b−a). Hence if a−b=xn and b−c=yn,  , then a−c=(x+y)n.
, then a−c=(x+y)n.
7. If n=pm and a≡b(mod n), then a−b=qn=qpm. Thus a≡b(modm).
8.
a. In  , so
, so  ,
, 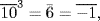
 . Since 515=6·85+5 we get
. Since 515=6·85+5 we get 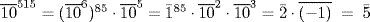 . Hence 10515≡5(mod7).
. Hence 10515≡5(mod7).
9.
a. In  , so
, so  . Since 1027=4·256+3, we get
. Since 1027=4·256+3, we get  . The unit decimal is 7.
. The unit decimal is 7.
11. 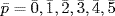 in
in  . If
. If  then 2
then 2  p; if
p; if  , then 3
, then 3  p. So
p. So  or
or  .
.
12.
a.  in
in  , so
, so  respectively.
respectively.
13.  in
in  . Taking each case separately:
. Taking each case separately:
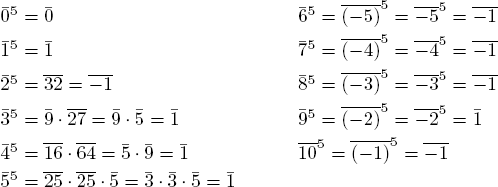
15. One of a, a+1 must be even so 2  a(a+1)(a+2); similarly, one of a, a+1, a+2 is a multiple of 3 [in fact a≡0 means 3
a(a+1)(a+2); similarly, one of a, a+1, a+2 is a multiple of 3 [in fact a≡0 means 3  a, a≡1 means 3
a, a≡1 means 3  a+2, and a≡2 means 3
a+2, and a≡2 means 3  a+1]. Hence 3
a+1]. Hence 3  a(a+1)(a+2). But 2 and 3 are relatively prime so 2·3=6 also divides a(a+1)(a+2). Hence
a(a+1)(a+2). But 2 and 3 are relatively prime so 2·3=6 also divides a(a+1)(a+2). Hence
![]()
17. Since  in
in  , we examine every case.
, we examine every case.

Hence  in all cases.
in all cases.
18.
a. Since  in
in  , it suffices to show each of these is a cube in
, it suffices to show each of these is a cube in 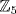 . Look at the cubes in
. Look at the cubes in  ,
,  ,
,  , and
, and  Thus every residue
Thus every residue  is a cube in
is a cube in  .
.
19.
a. Since  in
in 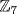 , we get
, we get  respectively. Clearly
respectively. Clearly  does not occur in
does not occur in  .
.
21. We have n=d0+10d1+102d2+ +10kdk.
+10kdk.
a.
![]()
22.
a. By the euclidean algorithm,

Hence (−8)·13≡1(mod35), so  is the inverse of
is the inverse of  in
in  . Then
. Then  gives
gives  .
.
c. Euclidean algorithm:

Hence the inverse of  is
is 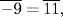 so
so  gives
gives  .
.
23.
a. Let  be the inverse of
be the inverse of 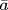 in
in 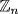 , so
, so  in
in  , then multiply
, then multiply  by
by  to get
to get 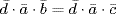 , that is
, that is  , that is
, that is 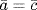 .
.
24.
a. If  and
and  are the inverses of
are the inverses of 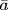 and
and 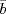 respectively in
respectively in  , then
, then  and
and  . Multiplying, we find
. Multiplying, we find  , that is
, that is  . Hence
. Hence  is the inverse of
is the inverse of  in
in 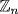 .
.
25.
a. Multiply equation 2 by  to get
to get 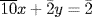 . Subtract this from equation 1:
. Subtract this from equation 1:  . But
. But  in
in  , so
, so 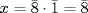 . Then equation 2 gives
. Then equation 2 gives  .
.
c. Multiply equation 2 by  to get
to get  . Comparing this with the first equation gives
. Comparing this with the first equation gives  an impossibility. So there is no solution to these equations in
an impossibility. So there is no solution to these equations in  (Compare with (a)).
(Compare with (a)).
e. Multiply equation 2 by  to get
to get  , which is just equation 1. Hence, we need only solve equation 2. If
, which is just equation 1. Hence, we need only solve equation 2. If 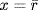 is arbitrary in
is arbitrary in 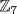 (so
(so  , then
, then 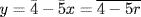 . Thus the solutions are:
. Thus the solutions are:
![]()
27. If an expression x2+ax is given where a is a number, we can complete the square by adding  . Then
. Then  . The same thing works in
. The same thing works in  except
except  is replaced by the inverse of
is replaced by the inverse of  if it exists.
if it exists.
a.  means
means  in
in  . The inverse of
. The inverse of  is
is  in
in  , so the square is completed by adding
, so the square is completed by adding  to both sides. The result is
to both sides. The result is
![]()
The only members of  which square to
which square to 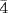 are
are  and
and  . (See Exercise 26.) Hence
. (See Exercise 26.) Hence 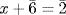 or
or  ; that is
; that is  or
or  .
.
c.  gives
gives  in
in  . The inverse of
. The inverse of  is
is  in
in  so add
so add  to both sides
to both sides
![]()
But  is not a square in
is not a square in 
 so there is no solution.
so there is no solution.
e. Since n is odd, gcd(2, n)=1, so  has an inverse in
has an inverse in 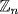 ; call it
; call it 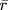 . Now
. Now  in
in 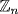 means
means  . Complete the square by adding
. Complete the square by adding  to both sides. The result is
to both sides. The result is
![]()
Thus, there is a solution if and only if  is a square in
is a square in  .
.
29.
a. Let  in
in 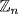 . If gcd(a, n)=1, then a has an inverse in
. If gcd(a, n)=1, then a has an inverse in  , say
, say  . Then
. Then  .
.
31. (1) ⇒ (2). Assume (1) holds but n is not a power of a prime. Then n=pka where p is a prime, k≥1, and a>1 has p  / a. Then gcd(n, a)=a>1, so
/ a. Then gcd(n, a)=a>1, so  has no inverse in
has no inverse in  . But
. But 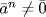 too. In fact
too. In fact 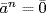 means n
means n  an whence p
an whence p  an. By Euclid's lemma, this implies p
an. By Euclid's lemma, this implies p  a, contrary to choice.
a, contrary to choice.
33. In 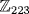 ,
,  . Thus
. Thus  ,
,  , and finally
, and finally  . Similarly, in
. Similarly, in  ,
,
![]()
34.
a. If ax≡b has a solution x in 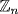 , then b−ax=qn, q an integer, so b=ax+qn. It follows that d=gcd(a, n) divides b. Conversely, if d
, then b−ax=qn, q an integer, so b=ax+qn. It follows that d=gcd(a, n) divides b. Conversely, if d  b write b=qd, q an integer. Now d=ra+sn for integers r and s (Theorem 3 §1.2), so b=qd=(qr)a+(qs)n. Thus, (qr)a≡b(modn) and we have our solution.
b write b=qd, q an integer. Now d=ra+sn for integers r and s (Theorem 3 §1.2), so b=qd=(qr)a+(qs)n. Thus, (qr)a≡b(modn) and we have our solution.
35. Working modulo p,  means
means  . Thus
. Thus  in
in  so
so  or
or  by Theorem 7.
by Theorem 7.
37.
a. If n=p2m and a=pm, then a6≡0(modn) and a2≡0(modn). Hence an6≡a.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
