1.1 Induction
1. In each case we give the equation that makes pk imply pk+1.
a. k(2k−1)+(4k+1)=2k2+3k+1=(k+1)(2k+1)
c.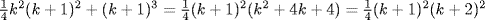 
e.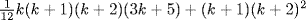 
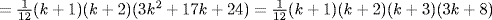
g.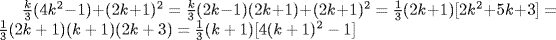 
7
7
i.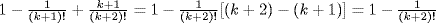 
2. In each case we give the inequality that makes pk imply pk+1.
a. 2k+1=2·2k>2·k≥k+1.
c. If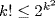 
, then 
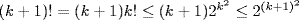provided k+1≤22k+1. This latter inequality follows, again by induction on k≥1, because 22k+3=4·22k+1≥4(k+1)≥k+2.
, then provided k+1≤22k+1. This latter inequality follows, again by induction on k≥1, because 22k+3=4·22k+1≥4(k+1)≥k+2.
e.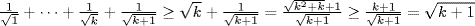 
.
.
3. In each case we give the calculation that makes pk imply pk+1.
a. If k3+(k+1)3+(k+2)3=9m, then (k+1)3 + (k+2)3 + (k+3)3 = 9m−k3 + (k+3)3 = 9m+9k2 + 27k + 27.
c. If 32k+1+2k+2=7m, then
5. If 33k+1=7m where k is odd, then passing to k+2,
7. It is clear if n=1. In general, such a (k+1) digit number must end in 4, 5 or 6, and there are 3k of each by induction. We are done since 3·3k=3k+1.
9. It is clear if n=1. Given k+1 secants, remove one and color the result unambiguously by induction. Now reinsert the removed secant. On one side of this secant, leave all regions the original color (including the new regions of that side created by the new secant). On the other side, interchange colors everywhere (including those regions newly created). This is an unambiguous coloring.
10.
a. If k≥2 cents can be made up, there must be a 2-cent or a 3-cent stamp. In the first case, replace a 2-cent stamp by a 3-cent stamp; in the second case, replace a 3-cent stamp by two 2-cent stamps.
c. If k≥18 can be made up, either one 7-cent stamp is used (replace with two 4-cent stamps) or five 4-cent stamps are used (replace with three 7-cent stamps).
11. a0=0 , a1=7, a2=63=7.9, a3=511=7·73. The conjecture is that 23n−1 is a multiple of 7 for all n≥0. If 23k−1=7x for some n≥0, then we have 23(k+1)−1=23(7x+1)−1=7(23+1).
12.
a. If Sn is the statement “13+23+33+
+n3 is a perfect square”, then S1 is true. If k≥1, assume that 13+23++k3=x2 for some integer x. Then 13+23++(k+1)3=x2+(k+1)3 and it is not clear how to deduce that this is a perfect square without some knowledge about how x is dependent upon k. Thus induction fails for Sn. However, if we strengthen the statement to 
, induction does go through (see Exercise 1(c)). The reason is that now the inductive hypothesis brings more information to the inductive step and so allows the (stronger) conclusion to be deduced.
+n3 is a perfect square”, then S1 is true. If k≥1, assume that 13+23++k3=x2 for some integer x. Then 13+23++(k+1)3=x2+(k+1)3 and it is not clear how to deduce that this is a perfect square without some knowledge about how x is dependent upon k. Thus induction fails for Sn. However, if we strengthen the statement to 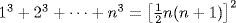, induction does go through (see Exercise 1(c)). The reason is that now the inductive hypothesis brings more information to the inductive step and so allows the (stronger) conclusion to be deduced.
13. 
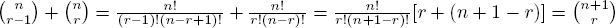
14.
a.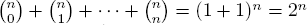
by the binomial theorem (Example 6 with x=1).
by the binomial theorem (Example 6 with x=1).
15. We use the well-ordering principle to prove the principle of induction. Let p1, p2, p3, be statements such that p1 is true and pk⇒pk+1 for every k≥1. We must show that pn is true for every n≥1. To this end consider the set X={n≥1 
pn is false}; we must show that X is empty. But if X is nonempty it has a smallest member m by the well-ordering principle. Hence m≠1 (because p1 is true), so m−1 is a positive integer. But then pm−1 is true (because m is the smallest member of X) and so pm is true (because pm−1⇒pm). This contradiction shows that X must be empty, as required.
be statements such that p1 is true and pk⇒pk+1 for every k≥1. We must show that pn is true for every n≥1. To this end consider the set X={n≥1 pn is false}; we must show that X is empty. But if X is nonempty it has a smallest member m by the well-ordering principle. Hence m≠1 (because p1 is true), so m−1 is a positive integer. But then pm−1 is true (because m is the smallest member of X) and so pm is true (because pm−1⇒pm). This contradiction shows that X must be empty, as required.
17. If pn is “n has a prime factor”, then p2 is true. Assume p2, . . ., pk are all true. If k+1 is a prime, we are done. If k+1=ab write 2≤a≤k and 2≤b≤k, then a (and b) has a prime factor by strong induction. Thus k+1 has a prime factor.
18.
a.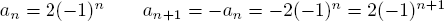
c.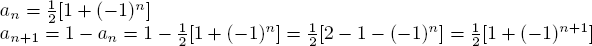 
19. Given n lines, another line intersects all existing lines (because no two are parallel) at new intersection points (none of these are concurrent) and so enters n+1 regions. Hence it creates n+1 new regions; so an+1=an+(n+1). Then a0=1, a1=1+1, a2=1+1+2, a3=1+1+2+3; and this suggests an=1+(1+2++n). Hence Gauss' formula (Example 1) gives
+n). Hence Gauss' formula (Example 1) gives
This is valid for n=0; if it holds for n=k≥1 then
21.
a. Let pn denote the statement an=(−1)n. Then p0 and p1 are true by hypothesis. If pk and pk+1 are true for some k≥0, then ak=(−1)k, ak+1=(−1)k+1 and so
Thus pk+2 is true and the principle applies.
23. p1⇒p2 fails.
24.
a. Prove p1 and p2 are true.
25. If pk is true for some k, then pk−1, pk−2, . . ., p1 are all true by induction using the first condition. Given m, the second condition implies that pk is true for some k≥m, so pm is true.
27. Apply the recursion theorem with s0=a0 and sn=sn−1+an.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.