8.4 The Sylow Theorems
1. Since |S4| = 23 · 3, the Sylow 3-subgroups are all cyclic of order 3, and thus have the form P =  γ
γ  , γ = (i j k). Now σ(123)σ−1 = (σ(1)σ(2) σ(3)) for all σ
, γ = (i j k). Now σ(123)σ−1 = (σ(1)σ(2) σ(3)) for all σ  S4 (Lemma 3 §2.8) so let
S4 (Lemma 3 §2.8) so let 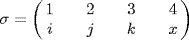 where {1, 2, 3, 4} = {i, j, k, x}. Then σ(123)σ−1 = (ijk) so γ and (1 2 3) are conjugate. Hence P and
where {1, 2, 3, 4} = {i, j, k, x}. Then σ(123)σ−1 = (ijk) so γ and (1 2 3) are conjugate. Hence P and  (123)
(123) are conjugate.
are conjugate.
3. P is a Sylow p-subgroup of N(P), being a p-subgroup of maximal order. It is unique because it is normal in N(P).
5. Let |G| = 1001 = 7 · 11 · 13. We have n7 = 1, 11, 13, 143 and n7 ≡ 1 (mod 7), so n7 = 1. Similarly n11 = 1, 7, 13, 91 and n11 ≡ 1 (mod 11), so n11 = 1; and n13 = 1, 7, 11, 77 and n13 ≡ 1 (mod 13) so n13 = 1. Thus let H  G, K
G, K  G, L
G, L  G have order |H| = 7, |K| = 11 and |L| = 13. Then H ∩ K = {1} so HK ≅ H × K ≅ C77. Now HK ∩ L = {1} so (HK)L ≅ HK × L ≅ C1001. Thus G = HKL ≅ C1001 is unique up to isomorphism.
G have order |H| = 7, |K| = 11 and |L| = 13. Then H ∩ K = {1} so HK ≅ H × K ≅ C77. Now HK ∩ L = {1} so (HK)L ≅ HK × L ≅ C1001. Thus G = HKL ≅ C1001 is unique up to isomorphism.
7.
a. If |G| = 40 = 23 · 5, then n5 = 1, 2, 4, 8 and n5 ≡ 1 (mod 5). Thus n5 = 1 so the Sylow 5-subgroup is normal.
c. If |G| = 48 = 24 · 3 and P is a Sylow 2-subgroup, then |G : P| = 3 so let θ : G → S3 be a homomorphism. Clearly ker θ ≠ {1}.
8. If |G| = 520 = 23 · 5 · 13, then n13 = 1, 2, 4, 8, 18, 20, 40, 80 and n13 ≡ 1 (mod 13), so n13 = 1, 40. Similarly n5 = 1, 2, 4, 8, 13, 26, 52, 104, and n5 ≡ 1 (mod 5) so n5 = 1, 26. If either n13 = 1 or n5 = 1 we are done. Otherwise there are 40 · 12 = 480 elements of order 13 and 26 · 4 = 104 elements of order 5, giving 480 + 104 = 584 in all, a contradiction.
9.
a. If |G| = 70 = 2 · 5 · 7 we have n5 = 1 and n7 = 1, so let P  G and Q
G and Q  G satisfy |P| = 5 and |Q| = 7. Thus since
G satisfy |P| = 5 and |Q| = 7. Thus since
![]()
Thus |G : PQ| = 2 so PQ  G.
G.
c. If |G| = 30 = 2 · 3 · 5, then n3 = 1, 10 and n5 = 1, 6. Let |P| = 3 and |Q| = 5. If P is not normal, there are 10 Sylow 3-subgroups in G, and hence 10 · 2 = 20 elements of order 3. Similarly if Q is not normal there are 6 · 4 = 24 elements of order 5. So P  G or Q
G or Q  G; either way PQ = H is a subgroup of G of index 2 (so H
G; either way PQ = H is a subgroup of G of index 2 (so H  G). Since |H| = 15, P
G). Since |H| = 15, P  H and Q
H and Q  H by Sylow's third theorem, so H = PQ ≅ P × Q ≅ C15.
H by Sylow's third theorem, so H = PQ ≅ P × Q ≅ C15.
10. a. If |G| = 385 = 5 · 7 · 11 then n11 = 1 and n7 = 1, so let P  G, Q
G, Q  G satisfy |P| = 11 and |Q| = 7. Then
G satisfy |P| = 11 and |Q| = 7. Then
![]()
and so |G : PQ| = 5. Since both P  G and Q
G and Q  G we have PQ
G we have PQ  G.
G.
11. a. If |G| = 105 = 3 · 5 · 7, then n7 = 1, 15 and n5 = 1, 21. Let |P| = 7 and |Q| = 5. If neither P nor Q is normal in G, then G has 15 · 6 = 90 elements of order 7 and 21 · 4 = 84 elements of order 5, a contradiction. So P  G or Q
G or Q  G, whence PQ is a subgroup and |PQ| = |P||Q| = 35 because P ∩ Q = {1}. Since |G : PQ| = 3, let θ : G → S3 have ker θ ⊆ PQ. Clearly | ker θ| ≠ 1, 5, 7 so ker θ = PQ and PQ
G, whence PQ is a subgroup and |PQ| = |P||Q| = 35 because P ∩ Q = {1}. Since |G : PQ| = 3, let θ : G → S3 have ker θ ⊆ PQ. Clearly | ker θ| ≠ 1, 5, 7 so ker θ = PQ and PQ  G. Finally |PQ| = 35 = 7 · 5 means P
G. Finally |PQ| = 35 = 7 · 5 means P  PQ and Q
PQ and Q  PQ, so PQ ≅ P × Q ≅ C35.
PQ, so PQ ≅ P × Q ≅ C35.
13. Let P be a Sylow p-subgroup of G. Then |P| = pn, and |G : P| = m because p > m. Thus, by Theorem 1 §8.3 there is a homomorphism θ : G → Sm with ker θ ⊆ P. If | ker θ| = pk then pn−k = |G/ker θ| divides m ! . Since p > m this means that k = n, whence P = ker θ  G.
G.
15. α(P) is clearly a p-subgroup of G so α(P) ⊆ a−1Pa for some a  G by Theorem 2. But a−1Pa = P here because P
G by Theorem 2. But a−1Pa = P here because P  G.
G.
17. For convenience, write N = N(P) . Let gP  N/P have order pk, g
N/P have order pk, g  N. We must show that g
N. We must show that g  P. We have
P. We have  so o(g) is a power of p. Thus
so o(g) is a power of p. Thus  g
g is a p-subgroup of N. Since P is a Sylow p-subgroup of N, Theorem 2 gives
is a p-subgroup of N. Since P is a Sylow p-subgroup of N, Theorem 2 gives  g
g  ⊆ a−1Pa for some a
⊆ a−1Pa for some a  N. But P
N. But P  N so a−1Pa = P. Thus g
N so a−1Pa = P. Thus g  P, and gP = P.
P, and gP = P.
18. a. We have P ⊆ N(P) ⊆ H. If a  N(H) then a−1Pa ⊆ a−1Ha = H, so P and a−1Pa are both Sylow p -subgroups of H. By Sylow's second theorem, h−1(a−1Pa)h = P for some h
N(H) then a−1Pa ⊆ a−1Ha = H, so P and a−1Pa are both Sylow p -subgroups of H. By Sylow's second theorem, h−1(a−1Pa)h = P for some h  H. Thus ah
H. Thus ah  N(P) ⊆ H, whence a
N(P) ⊆ H, whence a  H.
H.
19. If Q is also a Sylow p-subgroup of G, then Q = a−1Pa by Sylow's second theorem. If g  N(Q) then Q = g−1Qg; that is a−1Pa = g−1a−1Pag. This implies that aga−1
N(Q) then Q = g−1Qg; that is a−1Pa = g−1a−1Pag. This implies that aga−1  N(P) = P, whence g
N(P) = P, whence g  a−1Pa = Q.
a−1Pa = Q.
21. K is clearly a p-subgroup. If a  G and P is a Sylow p -subgroup, then aPa−1 is also a Sylow p-subgroup, so K ⊆ aPa−1. Hence a−1Ka ⊆ P; since P was an arbitrary Sylow p -subgroup, a−1Ka ⊆ K. Thus K
G and P is a Sylow p -subgroup, then aPa−1 is also a Sylow p-subgroup, so K ⊆ aPa−1. Hence a−1Ka ⊆ P; since P was an arbitrary Sylow p -subgroup, a−1Ka ⊆ K. Thus K  G. Now let H be any normal p-subgroup of G. If H is a normal p-subgroup of G, then H ⊆ aPa−1 for some a
G. Now let H be any normal p-subgroup of G. If H is a normal p-subgroup of G, then H ⊆ aPa−1 for some a  G. Thus H = a−1Ha ⊆ P; whence H ⊆ K.
G. Thus H = a−1Ha ⊆ P; whence H ⊆ K.
23. If k|n, let n = kd and a1 = ad. Then o(a1) = k and a1ba1 = adbad = b. Finally, let k = 2m1, 2(m1d) = kd = n = 2m, so m1d = m. Thus 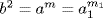 , and so
, and so  a1, b
a1, b  ≅ Qk.
≅ Qk.
25. If p and q are distinct primes, any group of one of the following orders is not simple: pn (Theorem 8 §8.2), pq (Example 5), p2q (Exercise 14) and p2q2 (Example 9). The only remaining orders (apart from primes) in the range 2–59 are as follows, with the reason that such a group G is not simple (We also include |G| = 36 —see Theorem 4).
| |G| | Reason |
| 24 = 23 · 3 | θ : G → S3 is not one-to-one |
| 30 = 2 · 3 · 5 | Exercise 9(c) |
| 40 = 23 · 5 | Exercise 7(a) |
| 42 = 2 · 3 · 7 | n7 = 1 |
| 48 = 24 · 3 | θ : G → S3 is not one-to-one |
| 54 = 2 · 33 | n3 = 1 |
| 56 = 23 · 7 | Example 7 |
| 36 = 22 · 32 | θ : G → S4 is not one-to-one |
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
