9.2 Solvable Groups
1. No. The group S4 is solvable (Example 4) but Z(S4) = {ε}.
3. No. S4 is solvable (Example 4) but  is not abelian. Indeed
is not abelian. Indeed  because S4/A4 is abelian. Thus
because S4/A4 is abelian. Thus  , {ε} or K = {ε, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)}. But S4/{ε} and S4/K are not abelian (see Exercise 30 §2.9).
, {ε} or K = {ε, (1 2)(3 4), (1 3)(2 4), (1 4)(2 3)}. But S4/{ε} and S4/K are not abelian (see Exercise 30 §2.9).
5. If G = A5 then G is not solvable being nonabelian and simple. Since |A5| = 60 = 22 · 3 · 5 the Sylow subgroups have orders 4, 3 or 5, and so are abelian.
7. G need not be solvable. If G = A5 × C2 then K = {ε} × C2 is an abelian normal subgroup which is maximal because G/K ≅ A5 is simple. But G is not solvable because A5 is not solvable.
8. 1. This is because α[a, b] = [α(a), α(b)] and the fact that G′ consists of products of commutators.
3. Every commutator from H is a commutator from G.
9. By Exercise 14 §8.4, let K  G where K ≠ {1}, G. If |G| = p2q let K
G where K ≠ {1}, G. If |G| = p2q let K  G, K ≠ {1}, K ≠ G. Then |K| = p, q, p2 or pq, so |G/K| = pq, p2, q or p. Thus both K and G/K are either abelian or of order pq, and hence are both solvable by Example 5. So G is solvable by Theorem 4.
G, K ≠ {1}, K ≠ G. Then |K| = p, q, p2 or pq, so |G/K| = pq, p2, q or p. Thus both K and G/K are either abelian or of order pq, and hence are both solvable by Example 5. So G is solvable by Theorem 4.
11. View F as an additive group and define θ : G → F ⊕ F by

Then θ is an onto homomorphism and 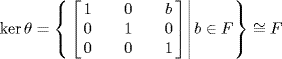 via
via  . Hence both ker θ and G/ker θ are abelian (hence solvable), so G is solvable.
. Hence both ker θ and G/ker θ are abelian (hence solvable), so G is solvable.
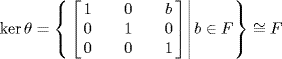 via
via  . Hence both ker θ and G/ker θ are abelian (hence solvable), so G is solvable.
. Hence both ker θ and G/ker θ are abelian (hence solvable), so G is solvable.
13. If odd order groups are solvable then the only odd order simple groups are abelian by Corollary 2 of Theorem 3. Hence the nonabelian simple finite groups have even order. Conversely, let |G| be odd. If G is abelian it is solvable. Otherwise it is not simple by hypothesis, so let K  G, K ≠ {1}, K ≠ G. Then both K and G/K have odd order less than |G|, so they are both solvable by induction. Thus G is solvable by Theorem 4.
G, K ≠ {1}, K ≠ G. Then both K and G/K have odd order less than |G|, so they are both solvable by induction. Thus G is solvable by Theorem 4.
15. If G is solvable and G = G0 ⊃ G1 ⊃  ⊃ Gp = {1} is a composition series, each simple factor is abelian and hence finite. Hence
⊃ Gp = {1} is a composition series, each simple factor is abelian and hence finite. Hence  is finite (see Exercise 11 §9.1). The converse holds because every finite group has a composition series.
is finite (see Exercise 11 §9.1). The converse holds because every finite group has a composition series.
17. If G/(H ∩ K) is solvable, so are its images G/H and G/K (by Theorem 7 §8.1). Hence G/H × G/K is solvable by Theorem 4. The converse is because G/(H ∩ K) is isomorphic to a subgroup of (G/H) × (G/K) via
![]()
19. a. HK is a subgroup because K  G, and
G, and  is solvable because
is solvable because  is solvable by Theorem 3 because H is solvable. Since K is solvable too, HK is solvable by Theorem 4.
is solvable by Theorem 3 because H is solvable. Since K is solvable too, HK is solvable by Theorem 4.
20. a. If G = {1}, it is solvable. If G ≠ {1} then Z1 = Z(G) ≠ {1} by hypothesis (with K = {1}). If Z1 ≠ G let  . Thus Z2 ⊃ Z1 and Z2
. Thus Z2 ⊃ Z1 and Z2  G. If Z2 ≠ G let
G. If Z2 ≠ G let  . So Z3
. So Z3  G, Z3 ⊃ Z2 ⊃ Z1 ⊃ {1}. Since G is finite, Zm = G for some m, so G = Zm ⊃
G, Z3 ⊃ Z2 ⊃ Z1 ⊃ {1}. Since G is finite, Zm = G for some m, so G = Zm ⊃  ⊃ Z1 ⊃ {1} is a solvable series for G.
⊃ Z1 ⊃ {1} is a solvable series for G.
21. a. It suffices to show that G′ ≠ G, since then G/G′ ≠ {1} is abelian. But if G′ = G then G(2) = (G′)′ = G′ = G, and it follows by induction that G(k) = G ≠ 1 for each k ≥ 0, and this cannot happen in a solvable group by Theorem 2.
22. (2) ⇒ (1). Assume (2). Then there exists G1  G such that
G such that  is abelian and G1 ⊂ G. If G1 = {1} we are done. If not let G2
is abelian and G1 ⊂ G. If G1 = {1} we are done. If not let G2  G1, G2 ⊂ G1,
G1, G2 ⊂ G1,  abelian. Thus G ⊃ G1 ⊃ G2. This process continues and, since G is finite, Gn = {1} at some stage. Then G ⊃ G1 ⊃ G2 ⊃
abelian. Thus G ⊃ G1 ⊃ G2. This process continues and, since G is finite, Gn = {1} at some stage. Then G ⊃ G1 ⊃ G2 ⊃  ⊃ Gn = {1} is a solvable series.
⊃ Gn = {1} is a solvable series.
23. Write R = R(G) and R1 = R(H).
a. Write {K  G
G  G/K solvable} = {K1, K2, . . ., Km}. This set is nonempty as it contains G. Then
G/K solvable} = {K1, K2, . . ., Km}. This set is nonempty as it contains G. Then  is normal and G/R is solvable by Exercise 18. If K
is normal and G/R is solvable by Exercise 18. If K  G and G/K solvable, then R ⊆ K by definition.
G and G/K solvable, then R ⊆ K by definition.
c. Define K = {k  G
G  α(k)
α(k)  R1}. We must show R ⊆ K. We have G → αH → ϕH/R1 where ϕ is the coset map, and
R1}. We must show R ⊆ K. We have G → αH → ϕH/R1 where ϕ is the coset map, and
![]()
This shows that K  G and G/K ≅ ϕα(G) ⊆ H/R1. Since H/R1 is solvable, this shows that G/K is solvable. It follows that R ⊆ K by definition.
G and G/K ≅ ϕα(G) ⊆ H/R1. Since H/R1 is solvable, this shows that G/K is solvable. It follows that R ⊆ K by definition.
24. Write S = S(G).
a. Write {K  G
G  K is solvable} = {K1, K2, . . ., Km}. This set is nonempty as it contains {1}. Now K1
K is solvable} = {K1, K2, . . ., Km}. This set is nonempty as it contains {1}. Now K1  G is solvable. Next K1K2
G is solvable. Next K1K2  G and is solvable by Exercise 19. If K1K2
G and is solvable by Exercise 19. If K1K2  Kn is normal and solvable, so is (K1K2
Kn is normal and solvable, so is (K1K2  Kn)Kn+1. Hence S is normal and solvable by induction. If K is normal and solvable then K = Ki for some i so K ⊆ S.
Kn)Kn+1. Hence S is normal and solvable by induction. If K is normal and solvable then K = Ki for some i so K ⊆ S.
c. α(S)  H because α is onto, and it is solvable by Theorem 3. Hence α(S) ⊆ S(H).
H because α is onto, and it is solvable by Theorem 3. Hence α(S) ⊆ S(H).
e. Write  Then K
Then K  G and K is solvable, so K ⊆ S by (a). Hence K = S and we are done.
G and K is solvable, so K ⊆ S by (a). Hence K = S and we are done.
25.
a. If G = G0 ⊃ G1 ⊃  ⊃ Gn = {1} is a solvable series, then Gi/Gi+1 is abelian so, by taking a subgroup of prime index repeatedly we get
⊃ Gn = {1} is a solvable series, then Gi/Gi+1 is abelian so, by taking a subgroup of prime index repeatedly we get
![]()
where  is of prime order. Piece these series together.
is of prime order. Piece these series together.
c. If G = G0 ⊃ G1 ⊃  ⊃ Gn = {1} has Gi/Gi+1 cyclic for all i, then Lemma 1 §9.1 shows that if K
⊃ Gn = {1} has Gi/Gi+1 cyclic for all i, then Lemma 1 §9.1 shows that if K  G then K and G/K have such a series because subgroups and images of cyclic groups are cyclic.
G then K and G/K have such a series because subgroups and images of cyclic groups are cyclic.
e. (iii) ⇒ (i). G is solvable and finitely generated because G  G. Now let G = G0 ⊃ G1 ⊃
G. Now let G = G0 ⊃ G1 ⊃  ⊃ Gn = {1} be a solvable series where Gi
⊃ Gn = {1} be a solvable series where Gi  G for all i (for example the derived series). Then each Gi is finitely generated by (iii) so Gi/Gi+1 is finitely generated and abelian. It is thus a direct product of cyclic groups by Theorem 3 §7.2 and so is polycyclic. Hence, piecing together series, we get a polycyclic series for G.
G for all i (for example the derived series). Then each Gi is finitely generated by (iii) so Gi/Gi+1 is finitely generated and abelian. It is thus a direct product of cyclic groups by Theorem 3 §7.2 and so is polycyclic. Hence, piecing together series, we get a polycyclic series for G.
27.
a. Write  . Then V
. Then V  G because the intersection of normal subgroups is normal. Note that the intersection is not empty because G
G because the intersection of normal subgroups is normal. Note that the intersection is not empty because G  G and G/G is in
G and G/G is in  . If V = K1 ∩ K2 ∩
. If V = K1 ∩ K2 ∩  ∩ Kn then G/V embeds in
∩ Kn then G/V embeds in  (as in Exercise 18) and
(as in Exercise 18) and  is in
is in  by induction because
by induction because  is closed under taking direct products. Hence G/V is in
is closed under taking direct products. Hence G/V is in  , being isomorphic to a subgroup of a group in
, being isomorphic to a subgroup of a group in 
c. If K  G and G/K is in
G and G/K is in  , we must show
, we must show  . Now
. Now  so
so  is in
is in  because
because  is in
is in  . Then
. Then 
28.
a. If k = 0 it is clear. Write  . If
. If  then, using the preceding exercise,
then, using the preceding exercise, 
c. If G is  -solvable let G = G0 ⊇ G1 ⊇
-solvable let G = G0 ⊇ G1 ⊇  ⊇ Gn = {1} be a
⊇ Gn = {1} be a  -series. Write
-series. Write 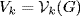 , and show Vk ⊆ Gk by induction on k. It is clear if k = 0. If Vk ⊆ Gk then
, and show Vk ⊆ Gk by induction on k. It is clear if k = 0. If Vk ⊆ Gk then 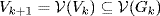 so it suffices to show that
so it suffices to show that  . But
. But 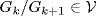 so this follows from the definition of
so this follows from the definition of  . The converse is clear because
. The converse is clear because 
e. If G is  -solvable and
-solvable and  for some H, then
for some H, then  for all k, contradicting (d). Conversely
for all k, contradicting (d). Conversely  for all k by hypothesis, so
for all k by hypothesis, so  . Since G is finite, it reaches {1}.
. Since G is finite, it reaches {1}.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
