10.2 The Main Theorem of Galois Theory
1.



a. 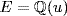 is the splitting field of x5 − 1 over
is the splitting field of x5 − 1 over 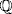 , and
, and  is separable as char
is separable as char  . By Example 4 §10.1,
. By Example 4 §10.1,  where σ(u) = u2 (because
where σ(u) = u2 (because  . The lattices are:
. The lattices are:

Thus H is the only intermediate field,
is the only intermediate field,  is Galois (as H
is Galois (as H  G), and
G), and  . We have σ2(u) = u4 = u−1 so σ2(u + u4) = (u + u4). Hence
. We have σ2(u) = u4 = u−1 so σ2(u + u4) = (u + u4). Hence  so, since
so, since  ,
, 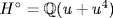 . Of course
. Of course 
c.  splits (x2 + 1)(x2 − 3) over
splits (x2 + 1)(x2 − 3) over  , so it is a Galois extension. Clearly x2 + 1 is the minimal polynomial of i, and has roots {i, − i} in E ; and x2 − 3 is the minimal polynomial of
, so it is a Galois extension. Clearly x2 + 1 is the minimal polynomial of i, and has roots {i, − i} in E ; and x2 − 3 is the minimal polynomial of  and has roots
and has roots  It follows by Theorem 1 that
It follows by Theorem 1 that  where G = gal(E : Q) . Construct
where G = gal(E : Q) . Construct 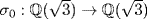 such that
such that  then extend σ0 to
then extend σ0 to  where σ(i) = − i. Hence σ
where σ(i) = − i. Hence σ  G and
G and  Similarly, construct
Similarly, construct 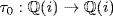 such that τ0(i) = i ; then extend τ0 to
such that τ0(i) = i ; then extend τ0 to 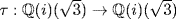 where
where  Hence τ
Hence τ  G and τ(i) = i. It follows easily that σ2 = ε and τ2 = ε, so
G and τ(i) = i. It follows easily that σ2 = ε and τ2 = ε, so 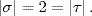 Now consider
Now consider 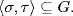 Since
Since 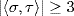 and
and  it follows that
it follows that  If H0 =
If H0 =  σ
σ  , H1 =
, H1 = τ
τ  and H2 =
and H2 =  στ
στ  , the lattices are
, the lattices are

Here each  is Galois (because Hi
is Galois (because Hi  G) and
G) and 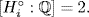 Hence
Hence  means
means 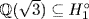 ; then
; then 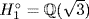 because
because  . Similarly
. Similarly  Finally,
Finally, 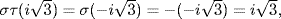 so
so 
e.  ,
, 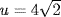 ; so
; so 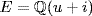 by Theorem 6 §10.1. Then E is the splitting field of x4 − 2 = (x − u)(x + u)(x − iu)(x + iu) so
by Theorem 6 §10.1. Then E is the splitting field of x4 − 2 = (x − u)(x + u)(x − iu)(x + iu) so  is Galois. By Exercise 13 §10.1,
is Galois. By Exercise 13 §10.1, 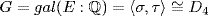 where o(σ) = 4, o(τ) = 2, στσ = τ and
where o(σ) = 4, o(τ) = 2, στσ = τ and 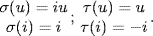 The lattice diagrams are:
The lattice diagrams are:

Here  σ2
σ2 ,
,  σ2, τ
σ2, τ  ,
,  σ
σ  and
and  σ2, τσ
σ2, τσ are normal in G (because
are normal in G (because  σ2
σ2  = Z(G)), so
= Z(G)), so  ,
,  ,
, 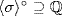 and
and  are Galois.
are Galois.
1.  : Hence σ2(i) = i; σ(u2) = − u2 so
: Hence σ2(i) = i; σ(u2) = − u2 so
![]()
Thus  . Also
. Also 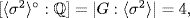 and so we are done because
and so we are done because  . Now
. Now  by Theorem 6 §10.1.
by Theorem 6 §10.1.
2.  : We have
: We have  ; and
; and 
3.  : We have τ(u2) = u2 and σ2(u2) = u2 (in (1)) so
: We have τ(u2) = u2 and σ2(u2) = u2 (in (1)) so 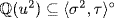 . But
. But 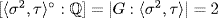 and
and 
4.  : Check
: Check  and
and 
5.  : Clearly
: Clearly 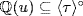 and
and  as x4 − 2 is irreducible.
as x4 − 2 is irreducible.
6.  : We have
: We have  as τσ(iu) = − u and τσ(u) = − iu. This is equality as x4 + 8 is the minimum polynomial of
as τσ(iu) = − u and τσ(u) = − iu. This is equality as x4 + 8 is the minimum polynomial of 
7.  : Compute
: Compute  ;
;  has minimum polynomial x4 − 2.
has minimum polynomial x4 − 2.
8.  : We have
: We have  because τσ3(u) = iu and τσ3(iu) = u. The minimum polynomial of
because τσ3(u) = iu and τσ3(iu) = u. The minimum polynomial of  is x4 + 8.
is x4 + 8.
2.


a. If G = gal(E : F) then |G| = p2 implies G is abelian, so  or G ≅ Cp × Cp by Theorem 7, §8.2. If
or G ≅ Cp × Cp by Theorem 7, §8.2. If  , the lattices are:
, the lattices are:

Here  σ2
σ2 
 ⊇ F is Galois because
⊇ F is Galois because  σ2
σ2 
 G, and [
G, and [ σ2
σ2 
 : F] = 2 . If G≅ Cp × Cp =
: F] = 2 . If G≅ Cp × Cp =  σ, τ
σ, τ  the lattices are:
the lattices are:

Each of  σ
σ 
 ⊇ F and
⊇ F and  τ
τ 
 ⊇ F are Galois because [
⊇ F are Galois because [ σ
σ 
 : F] =
: F] =  and [
and [ τ
τ 
 : F].
: F].
3. By Example 6 §10.1, 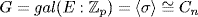 where σ : E → F is the Frobenius automorphism given by σ(u) = up. By the Dedekind-Artin theorem [E : G
where σ : E → F is the Frobenius automorphism given by σ(u) = up. By the Dedekind-Artin theorem [E : G ] = |G| = n. But
] = |G| = n. But 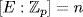 so, since
so, since  ,
,  . Thus
. Thus 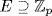 is a Galois extension by Lemma 4.
is a Galois extension by Lemma 4.
Now the (inverted) lattice of subgroups of G =  σ
σ  , when o(σ) = 12, is shown below at the right. Write Ek =
, when o(σ) = 12, is shown below at the right. Write Ek =  σk
σk 
 = {u
= {u  E
E  σk(u) = u} for each divisor k of n. Then the subfield lattice is shown below on the left.
σk(u) = u} for each divisor k of n. Then the subfield lattice is shown below on the left.
Note that
![]()
so |Ek| = pk, and Ek ≅ GF(pk).
4. a.  , σi
, σi  X,
X,  . Thus u
. Thus u  H is fixed by all τ
H is fixed by all τ  H if and only if σ(u) = u for all σ
H if and only if σ(u) = u for all σ  X.
X.
5. a. Let 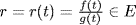 . Then
. Then
![]()
If char F = 2, this always holds and K = EG = E. Thus t  K so m = x − t. If char F ≠ 2, write h(t) = f(t)g(− t). Then h(t) = h(− t) so h(t) = k(t2) for some polynomial k (because char F ≠ 2) . Thus f(t)g(− t) = k(t2) . Similarly and g(t)g(− t) = l(t2) for some polynomial l. Thus
K so m = x − t. If char F ≠ 2, write h(t) = f(t)g(− t). Then h(t) = h(− t) so h(t) = k(t2) for some polynomial k (because char F ≠ 2) . Thus f(t)g(− t) = k(t2) . Similarly and g(t)g(− t) = l(t2) for some polynomial l. Thus  , from which K = F(t2) . It follows that m = x2 − t2. Note that this shows [E : K] = 2 = |G| in this case, as the Dedekind-Artin theorem guarantees.
, from which K = F(t2) . It follows that m = x2 − t2. Note that this shows [E : K] = 2 = |G| in this case, as the Dedekind-Artin theorem guarantees.
7. a. K′ is a subgroup of the abelian group G, so it is normal. Then the main theorem applies.
9.
a. If H → H is onto, and K is an intermediate field, then K = H
is onto, and K is an intermediate field, then K = H for a subgroup H, so K
for a subgroup H, so K ′ = H
′ = H ′
′ = H′ = K. Thus K is closed. Conversely, if all intermediate fields K are closed then K = K′
= H′ = K. Thus K is closed. Conversely, if all intermediate fields K are closed then K = K′ is the image of K′, and the map is onto.
is the image of K′, and the map is onto.
11. Write G = gal(E : F) = {σ  autE
autE  σ fixes F}. Since K ⊇ F we have
σ fixes F}. Since K ⊇ F we have
![]()
Thus:
| E ⊇ K is Galois | K is the set of elements of E fixed by gal(E : K) | |
| K = {u |
||
| K = K′ |
||
| K is closed in E ⊇ F . |
13. If [E : K] = 6 then  , so K′ is a subgroup of A4 of order 6. There is no such subgroup (Exercise 34 §2.6).
, so K′ is a subgroup of A4 of order 6. There is no such subgroup (Exercise 34 §2.6).
15. a. By its definition, K  L is the smallest intermediate field containing both K and L. Since the Galois connection K → K′ is order reversing, (K
L is the smallest intermediate field containing both K and L. Since the Galois connection K → K′ is order reversing, (K 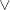 L)′ is the largest subgroup of G = gal(E : F) contained in both K′ and L′; that is (K
L)′ is the largest subgroup of G = gal(E : F) contained in both K′ and L′; that is (K 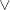 L)′ = K′ ∩ L′.
L)′ = K′ ∩ L′.
17. If K = σ(K1) let  . If
. If 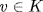 write
write  , u
, u  K1. Then
K1. Then
![]()
so σK′σ−1 ⊆ K′. On the other hand, if μ  K′ then
K′ then 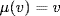 for all
for all  , so μ[σ(u)] = σ(u) for all u
, so μ[σ(u)] = σ(u) for all u  K1. Hence
K1. Hence 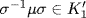 , so
, so  . This proves
. This proves 
Conversely, assume 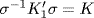 , that is
, that is 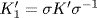 . If u
. If u  K1 then μ(u) = u for all
K1 then μ(u) = u for all  , so σ−1λσ(u) = u for all λ
, so σ−1λσ(u) = u for all λ  K′, that is λ[σ(u)] = σ(u) for all λ
K′, that is λ[σ(u)] = σ(u) for all λ  K′, that is σ(u)
K′, that is σ(u)  K′
K′ . Since E ⊇ F is Galois, K′
. Since E ⊇ F is Galois, K′ = K, so this shows σ(u)
= K, so this shows σ(u)  K, u
K, u  σ−1(K). Hence K1 ⊆ σ−1(K), so σ(K1) ⊆ K. Similarly K ⊆ σ(K1).
σ−1(K). Hence K1 ⊆ σ−1(K), so σ(K1) ⊆ K. Similarly K ⊆ σ(K1).
19. a. Let E = F(u1, u2, . . ., um) where X = {u1, u2, . . ., um} is the set of distinct roots of f in E. If σ  G then σ(ui)
G then σ(ui)  X for all i so σ : X → X is one-to-one (hence onto). Thus σ induces a permutation of these roots:
X for all i so σ : X → X is one-to-one (hence onto). Thus σ induces a permutation of these roots:
![]()
Now the map  is a group homomorphism G → Sm because
is a group homomorphism G → Sm because
![]()
for all σ, τ in G. Moreover 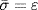 means σ(ui) = ui for all i, so σ = ε in G by Theorem 3 §10.1. Thus
means σ(ui) = ui for all i, so σ = ε in G by Theorem 3 §10.1. Thus  is an embedding.
is an embedding.
20.
a. If  then, given
then, given
![]()
But τσ traces all of G as σ does, so 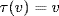 . This is true for all τ
. This is true for all τ  G, so
G, so 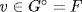 . The proof that T(u) is in F is analogous.
. The proof that T(u) is in F is analogous.
c. If K ⊇ F is Galois and H = gal(K : F), then |H| = n by Theorem 3, Corollary 3. Now p splits in K and has distinct roots u1, u2, . . ., um (Theorem 3). Hence p = (x − u1)(x − u2)  (x − un). For each i there exists σi
(x − un). For each i there exists σi  H such that σi(u) = ui, so p = ∏ σ
H such that σi(u) = ui, so p = ∏ σ G(x − σ(u)). Thus the coefficients of xn−1 and 1 are, respectfully
G(x − σ(u)). Thus the coefficients of xn−1 and 1 are, respectfully

21. If 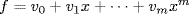 define
define  for τ
for τ  G. Thus fτ = ∏ σ
G. Thus fτ = ∏ σ G[x − τσ(u)] = f because τσ runs through G as σ does. It follows that
G[x − τσ(u)] = f because τσ runs through G as σ does. It follows that  for all τ
for all τ  G, whence
G, whence  for each j. Thus f
for each j. Thus f  F[x]. Since f(u) = 0, p|f where p is the minimal polynomial of u over F. Write f = pmg where p and g are relatively prime in F[x]. If g ≠ 1, let q be an irreducible factor of g. Since q|f, 0 = q[σ(u)] = σ[q(u)] for some σ
F[x]. Since f(u) = 0, p|f where p is the minimal polynomial of u over F. Write f = pmg where p and g are relatively prime in F[x]. If g ≠ 1, let q be an irreducible factor of g. Since q|f, 0 = q[σ(u)] = σ[q(u)] for some σ  G, so q(u) = 0. Since p(u) = 0 this is a contradiction because gcd(p, q) = 1 in F[x]. In fact, 1 = pr + qs gives 1 = 0 when we substitute x = u.
G, so q(u) = 0. Since p(u) = 0 this is a contradiction because gcd(p, q) = 1 in F[x]. In fact, 1 = pr + qs gives 1 = 0 when we substitute x = u.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
