1.4 Permutations
1.
a.
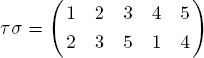
c.

e.

3.
a.

c.

e.
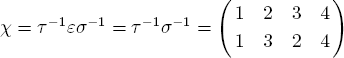
5. Solution 1. We must have σ1=1, 2, 3 or 4; in each case we find σ1=σ3, a contradiction.
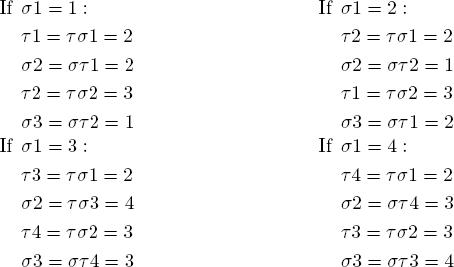
Solution 2. Let  . Then we show στ=(a b c d) is a cycle, contrary to στ=(1 2)(3 4):
. Then we show στ=(a b c d) is a cycle, contrary to στ=(1 2)(3 4):

6. If σk=k, then σ−1k=σ−1(σk)=k. If also τk=k, then (τσ)k=τ(σk)=τk=k.
7.
a. Here  where a, b, c, d are 2, 3, 4, 5 in some order. Thus there are 4 choices for a, 3 for b, 2 for c, and 1 for d; and so we have 4·3·2·1=4!=24 choices in all for σ.
where a, b, c, d are 2, 3, 4, 5 in some order. Thus there are 4 choices for a, 3 for b, 2 for c, and 1 for d; and so we have 4·3·2·1=4!=24 choices in all for σ.
b. Now  where a, b, c are 3, 4, 5 in some order. As in (a), there are 3·2·1=3!=6 choices in all for σ.
where a, b, c are 3, 4, 5 in some order. As in (a), there are 3·2·1=3!=6 choices in all for σ.
8.
a. If στ=ε, then σ=σε=σ(ττ−1)=(στ)τ−1=τ−1.
9. If σ=τ, then στ−1=ττ−1=ε; if στ−1=ε, then
![]()
11.
a. 
12.
a. ε, σ=(1 2 3), σ2=(1 3 2), τ=(1 2), στ=(1 3), σ2τ=(2 3). These are all six elements of S3. We have σ3=σσ2=ε, τ2=ε and hence τσ=(2 3)=σ2τ.
13.
a. σ=(1 4 8 3 9 5 2 7 6); σ−1=(1 6 7 2 5 9 3 8 4) (c) σ=(1 2 8)(3 6 7)(4 9 5); σ−1=(1 8 2)(3 7 6)(4 5 9) (e) σ=(1 3 8 7 2 5); σ−1=(1 5 2 7 8 3)
C. ε, (1 2 3 4 5), (1 2 3 4), (1 2 3), (1 2 3)(4 5), (1 2), (1 2)(3 4)
e. σ−1=(4 3 2 1)(7 6 5).
19. They are factored into disjoint cycles in the solution to Exercise 13, so the parities are:
![]()
21.
a. We have  for all i because the γi are transpositions. Hence (γ1γ2. . . γm)(γmγm−1. . . γ2γ2)=(γ1γ2. . . γm−1)(γm−1. . . γ2γ1)=. . .=ε. Now use Exercise 8(a).
for all i because the γi are transpositions. Hence (γ1γ2. . . γm)(γmγm−1. . . γ2γ2)=(γ1γ2. . . γm−1)(γm−1. . . γ2γ1)=. . .=ε. Now use Exercise 8(a).
c. If σ and τ are products of k and m transpositions respectively, then τ−1 is also a product of m transpositions (by (a)) so τστ−1 is a product of k+2m transpositions. This has the same parity as k.
23. Let σk=1 for some k≠1. Then, as n≥3, choose an m6 {k, 1}. Now let γ=(k, m). This gives γσk=γ1=1, but σγk=σm≠1, since if σm=1=σk, then m=k as σ is one-to-one, contrary to assumption.
{k, 1}. Now let γ=(k, m). This gives γσk=γ1=1, but σγk=σm≠1, since if σm=1=σk, then m=k as σ is one-to-one, contrary to assumption.
25. It suffices to show that any pair of transpositions is a product of 3-cycles. If k, l, m and n are distinct, this follows from
![]()
27.
a. Both sides have the same effect on each ki, and both sides fix each k∉{k1, k2, . . .kr}.
c. Using Exercise 26, we have for all a=1, 2, . . ., n−1:
![]()
Now if σ Sn, write it as a product of factors (1 n). Use (*) to write each (1 n) as a product of (1 2), . . ., (1 n−1), and (n−1 n). Then write each (1, n−1) in terms of (1 2), . . ., (1 n−2) and (n−2, n−1). Continue. The result is (c).
Sn, write it as a product of factors (1 n). Use (*) to write each (1 n) as a product of (1 2), . . ., (1 n−1), and (n−1 n). Then write each (1, n−1) in terms of (1 2), . . ., (1 n−2) and (n−2, n−1). Continue. The result is (c).
28.
a. σ=(1 2 3 4 . . . 2k−1 2k) so σ2=(1 3 5 . . . 2k−1)(2 4 6 . . . 2k).
c. The action of σ is depicted in the diagram, and carries k→k+1→k+2. . .. If k+m>n, the correct location on the circle is given by the remainder r when k+m is divided by n, That is k+m≡4(modn. Now the action of σm is σmk=k+m, so σmk≡k+mmodn.

29. Each of σ and τ may be either even or odd, so four cases arise. They are the rows of the following table. The parity of στ in each case is clear, and so the result follows

by verifying, sgn σ·sgnτ= sgn(τ) in every case.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
