2.11 An Application to Binary Linear Codes
1. (a) 5 (c) 6
2. (a) 3 (c) 7
3. By (1) of Theorem 1,
![]()
5. a. It suffices to look at individual digits:
![]()
6. The table lists the codewords across the top and the distances of  from them.
from them.

a. The unique nearest neighbor of 0110101 is 0100101 (so it corrects the single error).
c. 1011001 has both 1010101 and 1011010 at distance 2, so the 2 errors are detected but not corrected.
7. a. The minimum weight of C is 4. Detects 3 errors, corrects 1 error.
9.
a. We can have k = 4, n = 7 for the code, and (Example 9), the minimum weight for the code is 3. Thus it corrects t = 1 errors. Hence  shows the code is perfect.
shows the code is perfect.
c. If the minimum distance is 5 = 2 · 2 + 1, it corrects t = 2 errors. We have  while 27−2 = 25 = 32. So no such code exists.
while 27−2 = 25 = 32. So no such code exists.
10. a. If k = 2, t = 1, the Hamming bound is 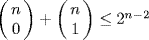 , that is 1 + n ≤ 2n−2. The first n ≥ 1 for which this holds n = 5. The
, that is 1 + n ≤ 2n−2. The first n ≥ 1 for which this holds n = 5. The  -code
-code  has minimum distance 3 = 2 · 1 + 1, so it corrects 1 error by Theorem 2.
has minimum distance 3 = 2 · 1 + 1, so it corrects 1 error by Theorem 2.
 has minimum distance 3 = 2 · 1 + 1, so it corrects 1 error by Theorem 2.
has minimum distance 3 = 2 · 1 + 1, so it corrects 1 error by Theorem 2.
11. a. Here k = 3 and t = 2, so n must be such that  If n = 3, 4, . . ., 8 this would read respectively>
If n = 3, 4, . . ., 8 this would read respectively>
![]()
Hence n ≥ 9. [Note: 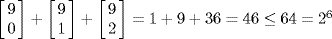 .]
.]
13. Suppose  is the coset leader in
is the coset leader in  , and write it as
, and write it as  . Then coset decoding decodes
. Then coset decoding decodes  as
as  , and this is correct. Conversely, assume coset decoding decodes
, and this is correct. Conversely, assume coset decoding decodes  correctly as c. If e is the coset leader in
correctly as c. If e is the coset leader in  , this means
, this means  . Hence
. Hence  is the coset leader in
is the coset leader in  .
.
15. a. If a (4, 2)-code C corrects 1 error, the weight of C must be at least 3. Thus the nonzero words of C are all contained in {1111, 1110, 1101, 1011, 0111}. But the sum of two distinct words here is no longer in the set.
16.
a. If a (6, 3)-code C corrects 2 errors, the weight of C must be at least 5. Proceed as in (a) of the preceding exercise.
c. If a (7, 3)-code C has minimum distance 5, the nonzero words in C have weight 7, 6 or 5. The table gives the possible weights of  for various choices of
for various choices of  and
and  (nonzero) in C. For example, if
(nonzero) in C. For example, if  and
and  both have weight 5, we may take
both have weight 5, we may take  . The weight of
. The weight of  depends upon how many 0-digits match. The three cases are illustrated as follows:
depends upon how many 0-digits match. The three cases are illustrated as follows:
![]()
The weight of  is 0, 2, 4 respectively The table shows that
is 0, 2, 4 respectively The table shows that  is not in C (unless
is not in C (unless  ), so no such group C can exist.
), so no such group C can exist.
| 7 | 7 | 0 |
| 7 | 6 | 1 |
| 7 | 5 | 2 |
| 6 | 6 | 0 2 |
| 6 | 5 | 1 3 |
| 5 | 5 | 0 2 4 |
17.
a. Write  and
and 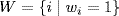 , so
, so  and
and 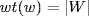 . Then
. Then
![]()
so  . Similarly
. Similarly
![]()
so  . Then (a) follows because
. Then (a) follows because

c. Using (a), equality holds in (b) if and only if wt(vw) = 0, that is if and only if V∩ W = . If this holds, then 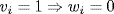 which is the condition in (c). Conversely, if
which is the condition in (c). Conversely, if  , then i
, then i  V ∩ W is impossible (it means
V ∩ W is impossible (it means 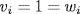 ), so V∩ W = . Thus wt(vw) = 0 and (a) implies equality in (b).
), so V∩ W = . Thus wt(vw) = 0 and (a) implies equality in (b).
19. We have  Hence it suffices to show that D is a subgroup of Bn. Clearly 0
Hence it suffices to show that D is a subgroup of Bn. Clearly 0  D and, if x
D and, if x  D, then −x = x
D, then −x = x  D. Finally, if x, y
D. Finally, if x, y  D consider the following cases: If x, y
D consider the following cases: If x, y  C then x + y
C then x + y  C because C is a subgroup. If x
C because C is a subgroup. If x  C and
C and  then
then  because x
because x  C. If
C. If 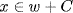 and y
and y  C then
C then  as in the preceding case. If
as in the preceding case. If  and
and  then
then  because
because 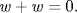 Hence
Hence  in every case.
in every case.
20.
a. 

c. 

1.
a.{0000, 1011, 0100, 1111}
c. {000000, 100101, 010110, 001001, 110011, 101100, 011111, 111010}
23. Write 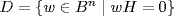 . We have C ⊆ D as before (by the Lemma). If
. We have C ⊆ D as before (by the Lemma). If  , write
, write 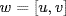 , u
, u  Bk,
Bk,  . Then
. Then
![]()
Thus 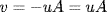 (because −x = x in Bn−k). Now
(because −x = x in Bn−k). Now
![]()
so  . Hence D ⊆ C.
. Hence D ⊆ C.
24. a. We have C = {uG  u
u  Bk} and C′ = {uG′
Bk} and C′ = {uG′  u
u  Bk}, so it is clear that G = G′ ⇒ C = C′. If C = C′, write G = {Ik, A] and G′ = {Ik′, A′]. Given u
Bk}, so it is clear that G = G′ ⇒ C = C′. If C = C′, write G = {Ik, A] and G′ = {Ik′, A′]. Given u  Bk, [u, uA] = uG
Bk, [u, uA] = uG  C, so there exists u′
C, so there exists u′  Bk such that [u, uA] = U′G′ = [u′, u′A′]. This gives u = u′ and uA = u′A′, so uA = uA′ for all u
Bk such that [u, uA] = U′G′ = [u′, u′A′]. This gives u = u′ and uA = u′A′, so uA = uA′ for all u  Bk. If u = bi is row i of Ik, then biA = row i of A and biA′ = row i of A′. Thus A = A′, whence G = G′.
Bk. If u = bi is row i of Ik, then biA = row i of A and biA′ = row i of A′. Thus A = A′, whence G = G′.
25.
a. Let  is even}. Define
is even}. Define 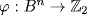 by
by 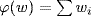 where
where  is digit i of
is digit i of  . Then ϕ is onto and (if
. Then ϕ is onto and (if  is digit i of
is digit i of  )
)
![]()
shows ϕ is a group homomorphism. Since
![]()
the fact that  shows that D is a subgroup of Bn of index 2. If C ⊆ D, then each word in C has even weight. Otherwise, choose c
shows that D is a subgroup of Bn of index 2. If C ⊆ D, then each word in C has even weight. Otherwise, choose c  C D and define σ : C ∩ D → C (C ∩ D) by σ(x) = x + c. [Clearly x + c
C D and define σ : C ∩ D → C (C ∩ D) by σ(x) = x + c. [Clearly x + c  C; if x + c
C; if x + c  D, then c
D, then c  D (as x
D (as x  D), a contradiction. So x + c
D), a contradiction. So x + c  C (C ∩ D). Since σ is clearly 1:1, it remains to show that σ is onto. If y
C (C ∩ D). Since σ is clearly 1:1, it remains to show that σ is onto. If y  C (C ∩ D), we want y = x + c, x
C (C ∩ D), we want y = x + c, x  C ∩ D. Try x = y − c. Clearly x
C ∩ D. Try x = y − c. Clearly x  C. Since y ∉ D and c ∉ D, we know ϕ(y) = 1 = ϕ(c), so ϕ(y − c) = 1 − 1 = 0. Thus x = y − c
C. Since y ∉ D and c ∉ D, we know ϕ(y) = 1 = ϕ(c), so ϕ(y − c) = 1 − 1 = 0. Thus x = y − c  D too.
D too.
c. Let D be any subgroup of Bn of index 2. Then C ⊆ D or [C : C ∩ D] = 2. The proof is in (a) where  has
has 
27. If  where {b1, . . ., bk} is a
where {b1, . . ., bk} is a  -basis of C, and if B → R by the gaussian algorithm, let ci be row i of R, 1 ≤ i ≤ k. There exists an invertible k × k matrix U (the product of the elementary matrices used to carry B → R) such that UB = R. If U = [uij], then row i of R is
-basis of C, and if B → R by the gaussian algorithm, let ci be row i of R, 1 ≤ i ≤ k. There exists an invertible k × k matrix U (the product of the elementary matrices used to carry B → R) such that UB = R. If U = [uij], then row i of R is
 where {b1, . . ., bk} is a
where {b1, . . ., bk} is a 
Since B = U−1R, we have bi  span{c1, . . ., cn} for each i, so C = span{c1, . . ., ck}. It follows that {c1, . . ., ck} is a basis of C. Since rank R = rankB = k, and since R is a reduced row-echelon matrix, the proof is complete.
span{c1, . . ., cn} for each i, so C = span{c1, . . ., ck}. It follows that {c1, . . ., ck} is a basis of C. Since rank R = rankB = k, and since R is a reduced row-echelon matrix, the proof is complete.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
