4.5 Symmetric Polynomials
1. The units in R[x1, . . ., xn] are just the units in R. If n = 1 this is Theorem 2 §4.1. In general, the units in R[x1, . . ., xn] = R[x1, . . ., xn−1][xn] are the units in R[x1, . . ., xn−1], so it follows by induction.
2. a.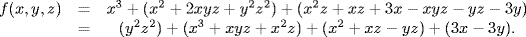 
3. f(x, y) = x + y + xy is symmetric but not homogeneous.
f(x, y) = x2y is homogeneous but not symmetric.
5. Given θ : R → S, any homomorphism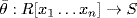 
with these properties must be given by
with these properties must be given by
because the ci are central in S, so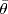 
is unique if it exists. But this formula defines a map R → S because the coefficients 
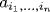are uniquely determined by the polynomial. Then it is routine to verify that 
is a homomorphism such that 
for all a 
R and 
for all i. This is what we wanted.
is unique if it exists. But this formula defines a map R → S because the coefficients are uniquely determined by the polynomial. Then it is routine to verify that is a homomorphism such that 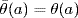for all a R and 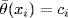for all i. This is what we wanted.
7. a. 
8.
a. By Theorem 4:
for some a, b, c.
If (x1, x2) = (1, 0) we get 0 = a.
If (x1, x2) = (1, 1) we get 2 = 32a + 8b + 2c.
If (x1, x2) = (1, 2) we get 12 = 35a + 27 · 2b + 3 · 22c.
The solution is a = b = 0, c = 1, so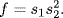 
c.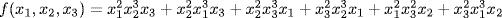 
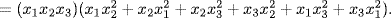Now observe that
Now observe that
Hence
= (x1x2x3)[(x1 + x2 + x3)(x1x2 + x1x3 + x2x3) − 3(x1x2x3)2
9. 
. The number of terms equals the number of k-subsets {i1, i2, . . ., ik} in the n-set {1, 2, · · · , n}. This is 
. Thus for example s3(x1, x2, x3, x4, x5) has 
terms:
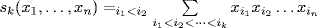. The number of terms equals the number of k-subsets {i1, i2, . . ., ik} in the n-set {1, 2, · · · , n}. This is 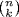. Thus for example s3(x1, x2, x3, x4, x5) has 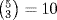terms:
10. The monomial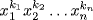 
has degree m = k1 + k2 + 
+ kn, ki ≥ 0. So we must count the number of n-tuples (k1, k2, . . ., kn) from 
with
has degree m = k1 + k2 + + kn, ki ≥ 0. So we must count the number of n-tuples (k1, k2, . . ., kn) from 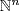with
Take m circles 0 and n − 1 dividers | and line them up. For example
The n − 1 dividers create n compartments (counting the ends). The number of circles in the ith compartment is ki. Thus the above lineup yields
So we must count lineups: there are n + m − 1 objects (circles and dividers). Label all the n + m − 1 positions and choose the m positions for circles in m + n − 1m ways. Voilà!
11.
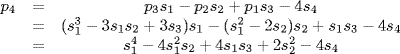
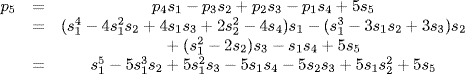
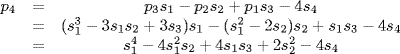
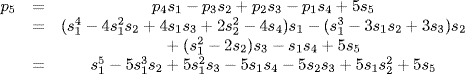
(Conjecture: If q is a prime,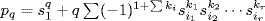 
summed over all ij such that 1 ≤ i1 < i2 < < ir ≤ q and 
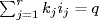. Over 
this implies that 
, which is true).
summed over all ij such that 1 ≤ i1 < i2 < < ir ≤ q and . Over this implies that 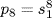, which is true).
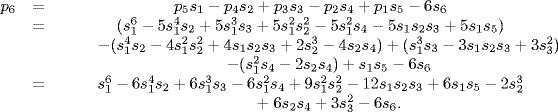
12.
a.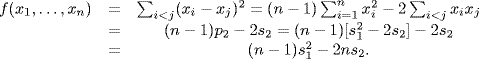 
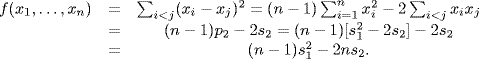
c.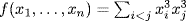 
. Now 
. Using the preceding exercise
. Now 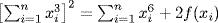. Using the preceding exercise
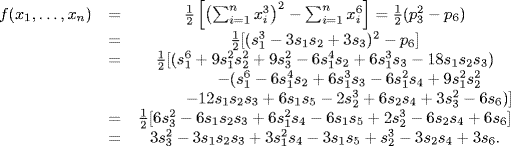
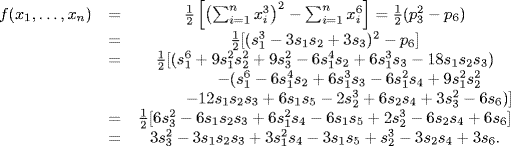
13.
a. We have
Hence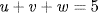 
, uv + uw + vw = 4, and uvw = 3. The polynomial we want is
, uv + uw + vw = 4, and uvw = 3. The polynomial we want is
Newton's formula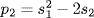 
gives
gives
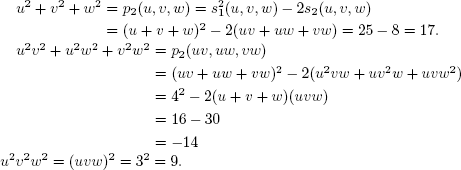
Hence x3 − 17x2 − 14x − 9 has roots u2,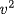 
, 
,
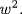
14.
a. Write f(xi)g(xi) = h(xi). Then
Similarly θσ(f + g) = θσ(f) + θσ(g) and θσ(1) = 1. Now
for all σ, τ and all f, so θστ = θσθτ. Similarly θ
= 1. In particular
= 1. In particular
Thus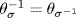 
and so θσ is a bijection.
and so θσ is a bijection.
c. If f, g SG then θ(f) = f and θ(g) = g for all θ G. Since θ is a ring homomorphism:
SG then θ(f) = f and θ(g) = g for all θ G. Since θ is a ring homomorphism:
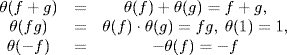
for all θ G. Thus SG is a subring. Note: SG is a subring for any subsetG of ring homomorphisms R → R.
G. Thus SG is a subring. Note: SG is a subring for any subsetG of ring homomorphisms R → R.
17. Prove this by induction on n. If n = 1 and f(a) = 0 for all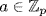 
then x, x − 1, . . ., x − p + 1 all divide f(x). Thus f(x) = x(x − 1) (x − p + 1)g(x), so °f(x) ≥ p, contrary to hypothesis. So f(a) ≠ 0 for some 
. If n ≥ 2 and 
write
then x, x − 1, . . ., x − p + 1 all divide f(x). Thus f(x) = x(x − 1) (x − p + 1)g(x), so °f(x) ≥ p, contrary to hypothesis. So f(a) ≠ 0 for some 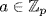. If n ≥ 2 and 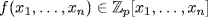write
Then pm ≠ 0 in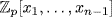 
so, by induction, let pm(a1, . . ., an−1) ≠ 0, 
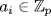. Write g(x) = f(a1, . . ., an−1, x). Then g(x) ≠ 0 so g(an) ≠ 0 for some 
by the case n = 1. This is what we wanted.
so, by induction, let pm(a1, . . ., an−1) ≠ 0, . Write g(x) = f(a1, . . ., an−1, x). Then g(x) ≠ 0 so g(an) ≠ 0 for some by the case n = 1. This is what we wanted.
17. If σ Sn,
Sn,
The polynomial p(x) has only odd exponents: p(x) = a1x+ a3x3 + . If f = Δng this gives f1 = a1Δng + a3(Δng)3 + = Δng(a1 + a3(Δng)2 + ). Since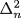 
is symmetric, g1 = g[a1 + a3(Δng)2 + a5(Δng)4 + ] is symmetric.
. If f = Δng this gives f1 = a1Δng + a3(Δng)3 + = Δng(a1 + a3(Δng)2 + ). Since is symmetric, g1 = g[a1 + a3(Δng)2 + a5(Δng)4 + ] is symmetric.
19.
a. a ≤ a is obvious; if a ≤ b and b ≤ a then, if a ≠ b and k is the smallest integer with ak ≠ bk, then ak < bk and bk < ak. This is impossible. Now suppose a ≤ b, b ≤ c. If a = b or b = c, we are done. If a < b and b < c let ak < bk, bl < cl where k is minimal with ak ≠ bk and l is minimal with bl ≠ cl. Let m = min (k, l). If i < m then ai = bi = ci by the choice of k and l.
Case 1. k = l. Then m = k = l so am < bm < cm.
Case 2. k < l. Then m = k < l so am < bm = cm.
Case 3. l < k. Then m = l < k so am = bm < cm.
Thus am < cm in any case, so a ≤ c.
c. Let X≠ ,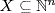 
. Write X1 = {x 
(x, . . .) X}. Then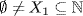 
so let m1 be the minimal element of X1. Now let X2 = {x (m1, x, . . .) X}, and let m2 be the minimal element of X2. Then let m3 be minimal in X3 = {x (m1, m2, x1, . . .) X}. Continue to get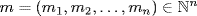 
. If 
, a ≠ m, consider two cases.
. Write X1 = {x (x, . . .) X}. Then so let m1 be the minimal element of X1. Now let X2 = {x (m1, x, . . .) X}, and let m2 be the minimal element of X2. Then let m3 be minimal in X3 = {x (m1, m2, x1, . . .) X}. Continue to get . If 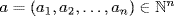, a ≠ m, consider two cases.
Case 1. a1 ≠ m1. Then m1 ≤ a1 by the choice of m1 so a ≤ m.
Case 2. a1 = m1. Let k be minimal such that mk ≠ ak. Then ai = mi, 1 ≤ i < k so a = (m1, m2, . . ., mk−1, ak, . . .). Thus mk ≤ ak by the choice of mk so m ≤ a. Thus m is the least member of X.
20.
a. If a, b G then |a| < 1 and |b| < 1, so |ab| = |a| |b| < 1. Thus 1 + ab > 0. We have
G then |a| < 1 and |b| < 1, so |ab| = |a| |b| < 1. Thus 1 + ab > 0. We have
so a ∗ b < 1 . Similarly
implies −1 < a ∗ b. Hence G is closed. The unity of G is 0 and the inverse of a is −a. Finally
This proves (a).
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.