4.4 Partial Fractions
1. Suppose r0+ r1p + 
= s0 + s1p + where p is monic in R[x] and each ri and si is either zero or has degree less than p. Then if ti = ri − si we have t0 + t1p + t2p2 + = 0, so t0 + (t1 + t2p + )p = 0. The uniqueness in the division algorithm (Theorem 4 §4.1) shows t0 = 0 and t1 + t2p + = 0. Then do it again to get t1 = 0 and t2 + t3p + = 0. This continues to show ti = 0 for all i.
= s0 + s1p + where p is monic in R[x] and each ri and si is either zero or has degree less than p. Then if ti = ri − si we have t0 + t1p + t2p2 + = 0, so t0 + (t1 + t2p + )p = 0. The uniqueness in the division algorithm (Theorem 4 §4.1) shows t0 = 0 and t1 + t2p + = 0. Then do it again to get t1 = 0 and t2 + t3p + = 0. This continues to show ti = 0 for all i.
2.
a. x2 − x + 1x(x2 + x + 1) = ax + bx + cx2 + x + 1, so
Evaluating at 0, 1 and −1 gives 1 = a, 1 = 3a + b + c, 3 = a + b − c. Hence a = 1, b = 0, c = − 2.
c. x + 1x(x2 + 1)2 = ax + bx + cx2 − 1 + dx + e(x2 + 1)2, so
Evaluating at 0, gives 1 = a; the coefficients x4, x3, x2, x give
and 1 = c + e. Thus a = e = 1, b = d = − 1 and c = 0.
3. 1(x − u1) · · · (x − un) = a1x − u1 + + anx − un, so
+ anx − un, so
Evaluation at uk gives 1 = ak ∏ i≠k(uk − ui), so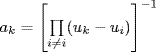 
for each k.
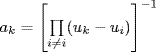for each k.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.