6.2 Algebraic Extensions
1.
a. 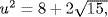 whence (u2 − 8)2 = 60 . Hence u4 − 16u + 4 = 0.
whence (u2 − 8)2 = 60 . Hence u4 − 16u + 4 = 0.
c.  so
so  that is
that is  Thus (u4 + 7)2 = 12u4, so u8 + 2u4 + 49 = 0.
Thus (u4 + 7)2 = 12u4, so u8 + 2u4 + 49 = 0.
2.
a.  so (u2 − 5)2 = 24, u4 − 10u2 + 1 = 0. We claim m = x4 − 10x2 + 1 is the minimal polynomial; it suffices to prove it is irreducible over
so (u2 − 5)2 = 24, u4 − 10u2 + 1 = 0. We claim m = x4 − 10x2 + 1 is the minimal polynomial; it suffices to prove it is irreducible over 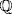 . It has no root in
. It has no root in 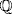 so suppose
so suppose
![]()
Then
![]()
Then c = − a and b = d = ± 1 . Hence 2b − a2 = − 10, so a2 = 10 + 2b = 12 or 8, a contradiction.
c. 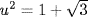 so (u2 − 1)2 = 3; u4 − 2u2 − 2 = 0. The minimal polynomial is x4 − 2x2 − 2 because it is irreducible by Eisenstein's criterion.
so (u2 − 1)2 = 3; u4 − 2u2 − 2 = 0. The minimal polynomial is x4 − 2x2 − 2 because it is irreducible by Eisenstein's criterion.
3.
a. A lgebraic; 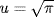 is a root of x2 − π F[x] where
is a root of x2 − π F[x] where 
c. Transcendental. For if f(π2) = 0 where 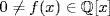 then g(π) = 0 where g(x) = f(x2) ≠ 0. This would imply π itself is algebraic over
then g(π) = 0 where g(x) = f(x2) ≠ 0. This would imply π itself is algebraic over  , a contradiction.
, a contradiction.
4.
a. (u − 1)2 = i2 = − 1, so u2 − 2u + 2 = 0. We claim m(x) = x2 − 2x + 2inF[x] is the minimal polynomial. The roots of m in 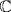 are 1 ± i and neither is in
are 1 ± i and neither is in 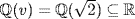 . Hence m(x) is irreducible in F[x].
. Hence m(x) is irreducible in F[x].
5. Clearly 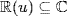 so
so  . Since
. Since 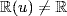 (because
(because 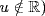 this means
this means  so
so 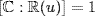 . Thus
. Thus 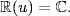 Alternatively, let u = a + bi. Then b ≠ 0 (as
Alternatively, let u = a + bi. Then b ≠ 0 (as  ) so
) so 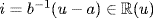 . Hence
. Hence 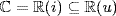 , so
, so  .
.
7.
a.  so
so 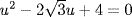 . We claim
. We claim
![]()
is the minimal polynomial. Its roots in  are
are 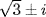 and neither is in
and neither is in 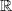 . So it is irreducible in
. So it is irreducible in  , as required.
, as required.
9. If 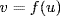 with f F[x], then
with f F[x], then 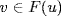 , whence
, whence 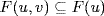 . Always
. Always  . Conversely, if
. Conversely, if 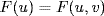 then
then  so
so
![]()
with ai F, n ≥ 1, by Theorem 4. Take f = a0 + a1x +  + an−1xn−1.
+ an−1xn−1.
11. If [F(u) : F] is finite then u is algebraic over F by Theorem 1 because u F(u). The converse follows from Theorem 4.
12.
a. If 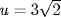 then u is a root of x3 − 2, which is irreducible over
then u is a root of x3 − 2, which is irreducible over 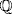 by the Eisenstein criterion. So the basis is {1, u, u2} by Theorem 4.
by the Eisenstein criterion. So the basis is {1, u, u2} by Theorem 4.
c. If 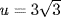 then u satisfies x3 − 3, which is irreducible over
then u satisfies x3 − 3, which is irreducible over  by Eisenstein. Thus {1, u, u2} is a basis of
by Eisenstein. Thus {1, u, u2} is a basis of 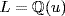 on
on 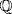 . We have
. We have 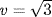 satisfies x2 − 3 L[x]. This is irreducible because
satisfies x2 − 3 L[x]. This is irreducible because 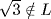 . [If
. [If  then
then 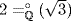 divides
divides  Thus
Thus 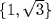 is a basis of
is a basis of  on L. By Theorem 5,
on L. By Theorem 5, 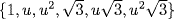 is a basis of E over
is a basis of E over 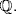
e. We have 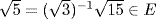 , so
, so 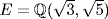 . Now
. Now  is a
is a  -basis of
-basis of 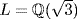 . We have
. We have 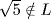 [If
[If  then b ≠ 0, and hence a ≠ 0]. Hence x2 − 5 is irreducible in L[x]. Thus
then b ≠ 0, and hence a ≠ 0]. Hence x2 − 5 is irreducible in L[x]. Thus 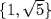 is an L-basis of
is an L-basis of 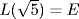 . Finally
. Finally  is a
is a  -basis of E by Theorem 5.
-basis of E by Theorem 5.
13.
a. Put 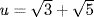 . Then
. Then  so u is a root of
so u is a root of  . The roots of m in
. The roots of m in  are
are 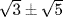 and these are not in F because
and these are not in F because 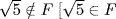 means
means 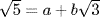 , a,
, a, 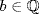 , and b ≠ 0 and
, and b ≠ 0 and 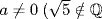 and
and 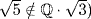 . Thus
. Thus 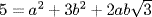 shows
shows 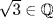 , a contradiction.] Thus m is irreducible over F, so [F(u) : F] = 2. But F(u) = E.
, a contradiction.] Thus m is irreducible over F, so [F(u) : F] = 2. But F(u) = E.
c. Put 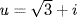 so (u − i)2 = 3 and u is a root of m = x2 − 2ix − 4 F[x]. The roots of m in
so (u − i)2 = 3 and u is a root of m = x2 − 2ix − 4 F[x]. The roots of m in 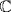 are u and
are u and 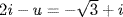 , and neither is in F because
, and neither is in F because  means
means 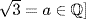 . Thus m is F-irreducible so E = F(u) has degree 2 over F; that is [E : F] = 2.
. Thus m is F-irreducible so E = F(u) has degree 2 over F; that is [E : F] = 2.
15. If u E, u ∉ F, we have E ⊇ F(u) ⊇ F, so [F(u) : F] divides [E : F] by Theorem 5. Since [F(u) : F] ≠ 1 because u ∉ F, we have [F(u) : F] = [E : F] because [E : F] is prime. Thus F(u) = E by Theorem 8 §6.1.
17. If F(u) ⊇ L ⊇ F write p = [F(u) : F] = [F(u) : L][L : F]. Thus [L : F] = 1 or p; so L = F or [L : F] = [F(u) : F], whence L = F(u) by Theorem 8 §6.1.
19. Let  . Then
. Then 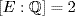 means f(u) = 0 where
means f(u) = 0 where  has degree 1 or 2. Since
has degree 1 or 2. Since 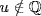 , °f = 2, say f = ax2 + bx + c. Thus
, °f = 2, say f = ax2 + bx + c. Thus 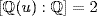 and
and 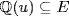 so
so 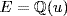 . Now f(u) = 0 so (clearing denominators) we may assume a, b and c are integers. Thus
. Now f(u) = 0 so (clearing denominators) we may assume a, b and c are integers. Thus 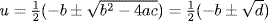 where
where 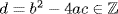 . Thus
. Thus 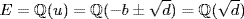 . If d = p2e,
. If d = p2e, 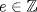 , p a prime, then
, p a prime, then  . Thus we can continue until
. Thus we can continue until  where m is square-free.
where m is square-free.
20.
a. E(u) ⊇ E ⊇ F gives E(u) ⊇ F finite because u is algebraic over E. Let m be the minimal polynomial of u over F, so [F(u) : F] = °m. Now u is also algebraic over E because m(u) E[x], so let p E(x) be the minimal polynomial of u over E. Since m(u) = 0, m E[u], Theorem 3 gives p|m. Thus [E(u) : E] = °p ≤ °m = [F(u) : F].
21.
a. Write L = F(u) so  . Now [L : F] = m by hypothesis so, since
. Now [L : F] = m by hypothesis so, since  , it suffices to show
, it suffices to show 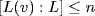 . Let p and m be the minimum polynomials of
. Let p and m be the minimum polynomials of  over L and F respectively. Then p|m by Theorem 3, so
over L and F respectively. Then p|m by Theorem 3, so
![]()
as required.
c. No. If 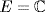 ,
, 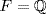 ,
, 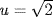 and
and 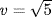 , then m = 2 and n = 2 are not relatively prime, but
, then m = 2 and n = 2 are not relatively prime, but 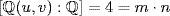 by Example 15.
by Example 15.
23. If 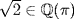 then
then 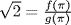 , f,
, f, 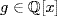 , gcd (f, g) = 1. Then h(π) = 0 where h(x) = 2g2(x) − f2(x), and this is a contradiction if h ≠ 0 in
, gcd (f, g) = 1. Then h(π) = 0 where h(x) = 2g2(x) − f2(x), and this is a contradiction if h ≠ 0 in 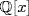 . But h = 0 means 2g2 = f2 so, since gcd(f, g) = 1, f|2. Thus f = ± 1, ±2, g2(x) = ± 1,
. But h = 0 means 2g2 = f2 so, since gcd(f, g) = 1, f|2. Thus f = ± 1, ±2, g2(x) = ± 1,  . This forces °g = 0;
. This forces °g = 0; 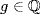 , g = ± 1,
, g = ± 1, 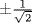 . Thus g = ± 1,
. Thus g = ± 1,  , a contradiction. Thus h ≠ 0 and
, a contradiction. Thus h ≠ 0 and 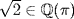 has led to a contradiction. So
has led to a contradiction. So 
25. Write K = F(u1, . . ., uk, . . ., un) and L = F(u1, . . ., uk). Then L ⊆ K becaue ui K for 1 ≤ i ≤ k, and so L(uk+1, . . ., un) ⊆ K because ui K for k + 1 ≤ i ≤ n. On the other hand F ⊆ L(uk+1, . . ., un) and every ui L(uk+1, . . ., un) because ui L if 1 ≤ i ≤ k. So K ⊆ L(uk+1, . . ., un).
26.
a. If u2 is algebraic over F, let f(u2) = 0, f(x) ≠ 0 in F[x]. Hence g(u) = 0 where g(x) = f(x2) ≠ 0. Thus u is algebraic over F.
27. Let  be a family of subfields of E and write
be a family of subfields of E and write
![]()
Then 1  F because 1
F because 1  Fi for all i. If a, b
Fi for all i. If a, b  F then a, b
F then a, b  Fi for all i, so a + b, a − b, ab are in Fi. Thus a + b, a − b, ab are in F, so F is a subring of E. Finally, if a ≠ 0 in F let ai be its inverse in Fi. Thus aai = 1 = aa−1 where a−1 is the inverse in E, so ai = a−1. Thus a−1
Fi for all i, so a + b, a − b, ab are in Fi. Thus a + b, a − b, ab are in F, so F is a subring of E. Finally, if a ≠ 0 in F let ai be its inverse in Fi. Thus aai = 1 = aa−1 where a−1 is the inverse in E, so ai = a−1. Thus a−1  Fi for all i, so a−1
Fi for all i, so a−1  F. Hence F is a field.
F. Hence F is a field.
29. Yes. Take 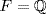 ,
,  and
and  . Then
. Then  by Exercise 23 and
by Exercise 23 and  is algebraic over
is algebraic over 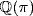 , being algebraic over
, being algebraic over 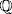 . On the other hand, π is transcendental over
. On the other hand, π is transcendental over 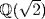 . For if f(π) = 0,
. For if f(π) = 0, 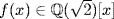 , write
, write
![]()
where either g(x) ≠ 0 or h(x) ≠ 0. Thus 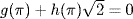 . If h(π) = 0 then g(π) = 0, g(x) ≠ 0, a contradiction. If h(π) ≠ 0 then
. If h(π) = 0 then g(π) = 0, g(x) ≠ 0, a contradiction. If h(π) ≠ 0 then  , contrary to Exercise 23.
, contrary to Exercise 23.
31.
a. We show F(u) = Q where
![]()
Since u is transcendental over F, f(u) ≠ 0 whenever f ≠ 0. Thus Q is a subfield of E containing F and u, so F(u) ⊆ Q. But any subfield of E containing F and u must contain Q, so F(u) ⊇ Q. Thus F(u) = Q.
c. Put  where a = f(u), g = g(u) as in (a). If h ≠ 0 in F[x] satisfies
where a = f(u), g = g(u) as in (a). If h ≠ 0 in F[x] satisfies 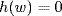 then, clearing denominators leads to a polynomial f(x, y) ≠ 0 in F[x, y] such that f(a, b) = 0. Write f(a, b) = ∑ ifi(a)bi. Then fi(a) = 0 for all i because b is transcendental; whence fi = 0 for all i because a is transcendental. So f(x, y) = 0; contrary to assumption.
then, clearing denominators leads to a polynomial f(x, y) ≠ 0 in F[x, y] such that f(a, b) = 0. Write f(a, b) = ∑ ifi(a)bi. Then fi(a) = 0 for all i because b is transcendental; whence fi = 0 for all i because a is transcendental. So f(x, y) = 0; contrary to assumption.
32.
a. Write 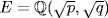 and
and  . Clearly
. Clearly 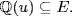 We have
We have  , so
, so
![]()
Substituting 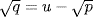 leads to
leads to  . Hence
. Hence  is in
is in 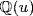 so, since p ≠ q,
so, since p ≠ q,  . Then
. Then  , so
, so 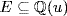 .
.
c. We have 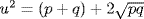 , so [u2 − (p + q)]2 = 4pq. This gives u4 − 2(p + q)u2 + (p + q)2 = 4pq, so u4 − 2(p + q)u2 + (p − q)2 = 0 . Thus f(u) = 0 where f = x4 − 2(p + q)x2 + (p − q)2. If m is the minimal polynomial of u over
, so [u2 − (p + q)]2 = 4pq. This gives u4 − 2(p + q)u2 + (p + q)2 = 4pq, so u4 − 2(p + q)u2 + (p − q)2 = 0 . Thus f(u) = 0 where f = x4 − 2(p + q)x2 + (p − q)2. If m is the minimal polynomial of u over  , this shows m|f. But
, this shows m|f. But 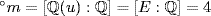 by (b), so we have m = f (as required) because both are monic.
by (b), so we have m = f (as required) because both are monic.
33. We show that if u is algebraic over A then u is algebraic over F, so u A contrary to hypothesis. If f(u) = 0 where f ≠ 0 in A[x], let
![]()
Then 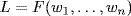 is a finite extension of F by Theorem 6. Moreover f L[x] so L(u) ⊇ L is a finite extension by Theorem 4. Thus L(u) ⊇ F is finite by Theorem 5, so u L(u) implies u is algebraic over F.
is a finite extension of F by Theorem 6. Moreover f L[x] so L(u) ⊇ L is a finite extension by Theorem 4. Thus L(u) ⊇ F is finite by Theorem 5, so u L(u) implies u is algebraic over F.
35.
a. Let 0 ≠ u R. Then u−1 exists in E and we must show it is in R. Now u is algebraic over F because E ⊇ F is an algebraic extension, so let f(u) = 0, 0 ≠ f F[x], say
![]()
If a0 = 0 we can cancel u to reduce the degree. So we may assume a0 ≠ 0. Clearly n ≥ 1. If n = 1, a1u + a0 = 0 gives u F so u−1 F ⊆ R. If n > 1 then u(anun−1 +  + a1) = − a0 so
+ a1) = − a0 so
![]()
c. If x and y are indeterminants over 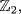 let
let  denote the field of fractions of the integral domain
denote the field of fractions of the integral domain 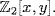 Then define
Then define 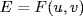 where u2 = x and
where u2 = x and  If R = span
If R = span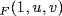 then E ⊇ R ⊇ F, R is an F -space, but R is not closed under multiplication; in fact uv ∉ R. For if uv R then uv = a + bu + cv where
then E ⊇ R ⊇ F, R is an F -space, but R is not closed under multiplication; in fact uv ∉ R. For if uv R then uv = a + bu + cv where  and so (since the characteristic is 2)
and so (since the characteristic is 2)
![]()
a contradiction because x and y are indeterminates over F.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
