5.1 Irreducibles and Unique Factorization
1. Let 0 ≠ a = bc. If a  b, say b = ua, then a = uac so 1 = uc, c is a unit, c
b, say b = ua, then a = uac so 1 = uc, c is a unit, c  1. If c
1. If c  1 then c is a unit so a = bc
1 then c is a unit so a = bc  b.
b.
3. a. 2 + i = i(1 − 2i) in  and i is a unit.
and i is a unit.
5. Let a  a′, b
a′, b  b′, say a′ = ua, b′ = vb. Then a′b′ = (uv)(ab) so a′b′
b′, say a′ = ua, b′ = vb. Then a′b′ = (uv)(ab) so a′b′  ab.
ab.
7. If  is a unit, 1 = N(u)N(u−1) = (a2 + 5b2) · N(u−1) shows a2 + 5b2 = 1. Thus u = ± 1.
is a unit, 1 = N(u)N(u−1) = (a2 + 5b2) · N(u−1) shows a2 + 5b2 = 1. Thus u = ± 1.
9. If  is maximal in P = {
is maximal in P = { 
 a ∉ R, a ∉ R∗}, let 83 p = ab. Then
a ∉ R, a ∉ R∗}, let 83 p = ab. Then  p
p ⊆
⊆  a
a so either
so either  a
a =
=  p
p or a ∉ R∗; that is a
or a ∉ R∗; that is a  p or a
p or a  1. Thus p is irreducible. Conversely, if p is irreducible and
1. Thus p is irreducible. Conversely, if p is irreducible and  p
p ⊆
⊆  a
a , a ∉ R∗, then p = ab where b is a unit. Hence a = pb−1
, a ∉ R∗, then p = ab where b is a unit. Hence a = pb−1  p
p , so
, so  p
p =
=  a
a .
.
10.
a. 11 is irreducible. If 11 = xy then 112 = |x|2|y|2 so |x|2, |y|2 each are 1, 11, 112. If |x|2 = 1 then x is a unit. So we rule out |x|2 = 11 = |y|2. If x = a + bi, this asks that a2 + b2 = 11. There are no such integers a, b.
c. 5 is not irreducible. We have 5 = (2 − i)(2 + i) and neither 2 − i nor 2 + i is a unit.
11. If p ≡ 3 (mod 4), suppose p = ab in 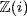 . Then p2 = |a|2|b|2. Since |x| = 1 in
. Then p2 = |a|2|b|2. Since |x| = 1 in  means x is a unit, it suffices to show that |a|2 = p is impossible in
means x is a unit, it suffices to show that |a|2 = p is impossible in  if a = m + in. This means m2 + n2 = p, whence m2 + n2 = 0 in
if a = m + in. This means m2 + n2 = p, whence m2 + n2 = 0 in  . If (say) m ≠ 0 in
. If (say) m ≠ 0 in  , this gives 1 + (m−1n)2 = 0 in
, this gives 1 + (m−1n)2 = 0 in  . This cannot happen (Corollary to Theorem 8 §1.3) because p ≡ 3 (mod 4). Hence m = 0 and a = 0 in
. This cannot happen (Corollary to Theorem 8 §1.3) because p ≡ 3 (mod 4). Hence m = 0 and a = 0 in  ; that is p|m and p|n. But then m2 + n2 = p implies p|1, a contradiction.
; that is p|m and p|n. But then m2 + n2 = p implies p|1, a contradiction.
12.
a. If  then N(p) = 62 + 5 · 12 = 41 is a prime. So p = ab in
then N(p) = 62 + 5 · 12 = 41 is a prime. So p = ab in  means 41 = N(p) = N(a)N(b). Thus N(a) = 1 or N(b) = 1. This means a or b is a unit (if
means 41 = N(p) = N(a)N(b). Thus N(a) = 1 or N(b) = 1. This means a or b is a unit (if  , then 1 = N(a) = m2 + 5n2 implies a = ± 1). So p is irreducible.
, then 1 = N(a) = m2 + 5n2 implies a = ± 1). So p is irreducible.
c. We have  in
in  . Since the only units in
. Since the only units in  are ±1, this shows 29 is not irreducible in
are ±1, this shows 29 is not irreducible in 
13. a. If 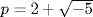 , suppose p = ab in
, suppose p = ab in 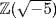 . Then 9 = N(p) = N(a)N(b). But N(a) = 3 is impossible in
. Then 9 = N(p) = N(a)N(b). But N(a) = 3 is impossible in  (because m2 + 5n2 ≠ 3 for m,
(because m2 + 5n2 ≠ 3 for m,  , so N(a) = 1 or N(b) = 1. Thus a = ± 1 or b = ± 1, and we have shown that p is irreducible in
, so N(a) = 1 or N(b) = 1. Thus a = ± 1 or b = ± 1, and we have shown that p is irreducible in  . To see that it is not prime, the fact that N(p) = 9 gives
. To see that it is not prime, the fact that N(p) = 9 gives  . So if p is prime, then p|3 in
. So if p is prime, then p|3 in  , say 3 = p · q. Then 9 = N(3) = N(p)N(q) = 9N(q) so N(q) = 1. This means q = ± 1, whence
, say 3 = p · q. Then 9 = N(3) = N(p)N(q) = 9N(q) so N(q) = 1. This means q = ± 1, whence  , a contradiction. So p is not prime.
, a contradiction. So p is not prime.
14.
a.  in
in  and neither factor is a unit (that is ±1). So p is not irreducible.
and neither factor is a unit (that is ±1). So p is not irreducible.
b. If p = 5 = ab in  then 25 = N(p) = N(a)N(b). Since N(a) = 5 is impossible in
then 25 = N(p) = N(a)N(b). Since N(a) = 5 is impossible in 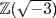 (because m2 + 3n2 = 5 is impossible with m,
(because m2 + 3n2 = 5 is impossible with m,  , either N(a) = 1 or N(b) = 1; that is a = ± 1 or b = ± 1. So 5 is irreducible.
, either N(a) = 1 or N(b) = 1; that is a = ± 1 or b = ± 1. So 5 is irreducible.
15. If  then p = ab means 4 = N(p) = N(a)N(b). Since m2 + 3n2 = 2 is impossible for m,
then p = ab means 4 = N(p) = N(a)N(b). Since m2 + 3n2 = 2 is impossible for m,  , we have N(a) ≠ 2 and N(b) ≠ 2. So N(a) = 1 or N(b) = 1; that is a = ± 1 or b = ± 1. Thus p is irreducible. If p is prime then
, we have N(a) ≠ 2 and N(b) ≠ 2. So N(a) = 1 or N(b) = 1; that is a = ± 1 or b = ± 1. Thus p is irreducible. If p is prime then  shows that p|2 in
shows that p|2 in  , say 2 = pq. Thus 4 = N(p)N(q) = 4N(q), whence N(q) = 1, q = ± 1, 2 = ± p, a contradiction. So p is not prime.
, say 2 = pq. Thus 4 = N(p)N(q) = 4N(q), whence N(q) = 1, q = ± 1, 2 = ± p, a contradiction. So p is not prime.
16. a. If p  q, suppose p is irreducible. If q = ab in R then p
q, suppose p is irreducible. If q = ab in R then p  ab so p
ab so p  a or p
a or p  b. Thus q
b. Thus q  a or q
a or q  b, so q is irreducible. The converse is proved the same way.
b, so q is irreducible. The converse is proved the same way.
17. Assume 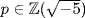 and N(p) is as in Example 3. If N(p) is a prime and p = xy in R, then N(p) = N(x)N(y). It follows that N(x) = 1 or N(y) = 1, say N(x) = 1. If
and N(p) is as in Example 3. If N(p) is a prime and p = xy in R, then N(p) = N(x)N(y). It follows that N(x) = 1 or N(y) = 1, say N(x) = 1. If 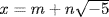 , this means m2 + 5n2 = 1, whence x = ± 1 is a unit. This shows that p is irreducible.
, this means m2 + 5n2 = 1, whence x = ± 1 is a unit. This shows that p is irreducible.
19. Suppose R is an integral domain with the DCCP. If a ≠ 0 in R, we have  a
a ⊇
⊇  a2
a2 ⊇
⊇  a3
a3
 so, by hypothesis, there exists a ≥ 1 such that
so, by hypothesis, there exists a ≥ 1 such that  an
an =
=  an+1
an+1 . Thus an
. Thus an 
 an+1
an+1 = Ran+1, say an = ban+1. Since a ≠ 0 and R is a domain, this gives 1 = ba, so a is a unit. This shows that R is a field. The converse is clear as a field has only two ideals.
= Ran+1, say an = ban+1. Since a ≠ 0 and R is a domain, this gives 1 = ba, so a is a unit. This shows that R is a field. The converse is clear as a field has only two ideals.
21. If R has the ACCP, suppose F has no maximal member. Choose  a1
a1 inF. Then
inF. Then  a1
a1 is not maximal so
is not maximal so  a1
a1 ⊂
⊂  a2
a2 for some
for some  a2
a2 in F. Now
in F. Now  a2
a2 is not maximal, so
is not maximal, so  a2
a2 ⊂
⊂  a3
a3 for some
for some  a3
a3 in F. This continues to violate the ACCP. Conversely, suppose
in F. This continues to violate the ACCP. Conversely, suppose  a1
a1 ⊆
⊆  a2
a2 ⊆
⊆  and let F = {
and let F = {  ai
ai
 i = 1, 2, . . . }. By hypothesis, let
i = 1, 2, . . . }. By hypothesis, let  an
an be maximal in F. If m ≥ n then
be maximal in F. If m ≥ n then  an
an ⊆
⊆  am
am so the maximality gives
so the maximality gives  an
an =
=  am
am . Thus R has the ACCP by Lemma 1.
. Thus R has the ACCP by Lemma 1.
23. No.  is a subring of the UFD
is a subring of the UFD  which is itself not a UFD by Example 5 (and Theorem 7).
which is itself not a UFD by Example 5 (and Theorem 7).
24. a Write d = gcd (a, b, . . .). Then d|0, d|a, d|b, . . .; if r|0, r|a, r|b, . . . then r|d by definition. So d  gcd (0, a, b, . . .) . Clearly 0|0, a|0, b|0, . . .; if 0|r, a|r, b|r, . . . then r = 0 (because 0|r) so 0
gcd (0, a, b, . . .) . Clearly 0|0, a|0, b|0, . . .; if 0|r, a|r, b|r, . . . then r = 0 (because 0|r) so 0  lcm(0, a, b, . . .) by definition.
lcm(0, a, b, . . .) by definition.
25. a Write d = gcd (a1, . . ., an) and d′ = gcd (b1, . . ., bn). Then d|ai for all i so d|bi for all i (Exercise 2), whence d|d′. Similarly, d′|d, whence d′  d.
d.
27. Write d = gcd [a, gcd (b, c)] and d′ = gcd [gcd (a, b), c]. Then d divides a and gcd (b, c) so it divides all of a, b, c. Thus d divides gcd (a, b) and c, whence d|d′. Similarly d′|d so d  d′. Moreover we have shown that d|a, d|b, d|c. If r|a, r|b and r|c then r divides a and gcd (b, c) so r|d. Hence gcd (a, b, c, ) exists and d
d′. Moreover we have shown that d|a, d|b, d|c. If r|a, r|b and r|c then r divides a and gcd (b, c) so r|d. Hence gcd (a, b, c, ) exists and d  gcd (a, b, c).
gcd (a, b, c).
29. It is clear if c = 0. Let  ,
,  and
and  . Then a|bc means ai ≤ bi + ci for all i, and gcd (a, b)
. Then a|bc means ai ≤ bi + ci for all i, and gcd (a, b)  1 means min (ai, bi) = 0 for all i. For each i, min (ai, bi) = 0 means ai = 0 or bi = 0. Thus ai ≤ ci in either case (because ai ≤ bi + ci) so a|c.
1 means min (ai, bi) = 0 for all i. For each i, min (ai, bi) = 0 means ai = 0 or bi = 0. Thus ai ≤ ci in either case (because ai ≤ bi + ci) so a|c.
31. If m  lcm(a1, . . ., an) exists in R then ai|m for each i shows
lcm(a1, . . ., an) exists in R then ai|m for each i shows  m
m ⊆
⊆  ai
ai for each i, and hence that
for each i, and hence that  m
m ⊆ A where we write A =
⊆ A where we write A =  ai
ai ∩
∩  ∩
∩  an
an . But r
. But r  A means ai|r for each i, so m|r by definition. Thus r
A means ai|r for each i, so m|r by definition. Thus r
 m
m and we have
and we have  m
m = A. Conversely, if A =
= A. Conversely, if A = m
m then ai|m for each i (because m
then ai|m for each i (because m 
 ai
ai ); and, if ai|r for each i, then r
); and, if ai|r for each i, then r A =
A =  m so m|r. Thus m is a least common multiple of the ai.
m so m|r. Thus m is a least common multiple of the ai.
33. 1.If the nonzero coefficients of f are a1, a2, . . ., an, then
![]()
Write c = c(f) and ai = cbi for each i. Then f = c · f1 where the nonzero coefficients of f1 are b1, . . ., bn. By Exercise 26, we have
![]()
so gcd (b1, . . ., bn)  1 as required.
1 as required.
34.
a. If p  R is irreducible in R, let p = ab in S. Then a
R is irreducible in R, let p = ab in S. Then a  R and b
R and b  R by (2) so a or b is a unit in R. Hence a or b is a unit in S, and p is irreducible in S. Conversely, if p is irreducible in S, let p = ab in R. Then one of a, b is a unit in S whence a or b is a unit in R by (1). So p is irreducible in R.
R by (2) so a or b is a unit in R. Hence a or b is a unit in S, and p is irreducible in S. Conversely, if p is irreducible in S, let p = ab in R. Then one of a, b is a unit in S whence a or b is a unit in R by (1). So p is irreducible in R.
b. Take S = R[x] above. Then (1) holds because units in R[x] are units in R, and (2) holds because fg  R with f, g in R[x] implies °f = 0 = °g, that is f
R with f, g in R[x] implies °f = 0 = °g, that is f  R and g
R and g  R. Now (b) gives (c).
R. Now (b) gives (c).
35. Suppose f = gh, h  R[x]. Then Gauss' lemma gives c(g)c(h)
R[x]. Then Gauss' lemma gives c(g)c(h)  c(f)
c(f)  1. Hence c(g)c(h) is a unit, so c(g) is a unit. This means g is primitive.
1. Hence c(g)c(h) is a unit, so c(g) is a unit. This means g is primitive.
37. If f  g in R[x] then f = ug, u a unit in R[x]. Thus u is a unit in F[x] so f
g in R[x] then f = ug, u a unit in R[x]. Thus u is a unit in F[x] so f  g in F[x]. Conversely, let f = ug, u a unit in F[x]. Then u
g in F[x]. Conversely, let f = ug, u a unit in F[x]. Then u  F, say
F, say  . Thus bf = ag in R so, since f and g are primitive,
. Thus bf = ag in R so, since f and g are primitive,
![]()
If a = bv,  , then bf = ag gives f = vg, that is f
, then bf = ag gives f = vg, that is f  g in R[x].
g in R[x].
39. a. We have  . This is a subring of
. This is a subring of  because
because
![]()
Thus R is an integral domain because  is.
is.
40.
a. R is a subring of  , hence a domain. If f
, hence a domain. If f  R is a unit in R, it is a unit in
R is a unit in R, it is a unit in  , hence a unit in
, hence a unit in  , hence a unit in
, hence a unit in  (since the constant coefficient cc(f) of f is in
(since the constant coefficient cc(f) of f is in 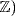 . Now each of the following is a nontrivial factorization in R.
. Now each of the following is a nontrivial factorization in R.  . Thus
. Thus  so the ACCP fails for R. Hence R is not a UFD.
so the ACCP fails for R. Hence R is not a UFD.
c. Let h be irreducible in R and suppose h|fg in R, say
![]()
where m,  ; f1,
; f1, 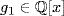 . If h = p is prime in
. If h = p is prime in  then p|m, say m = pm1. Thus
then p|m, say m = pm1. Thus  , that is h|f. So assume h = 1 + xh1,
, that is h|f. So assume h = 1 + xh1,  and h is irreducible in
and h is irreducible in  . Then h is prime in
. Then h is prime in  since
since 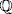 is a field, so h|f or h|g, say f = kh,
is a field, so h|f or h|g, say f = kh,  . But then the constant coefficient of k is m, the constant coefficient of f in
. But then the constant coefficient of k is m, the constant coefficient of f in 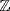 , so h|f in R.
, so h|f in R.
e. Write f = xnf1, n ≥ 0, cc(f1) ≠ 0. Since  write f1 = q1. . . qr, qi irreducible in
write f1 = q1. . . qr, qi irreducible in  . Let ti = cc(qi). Then t = t1. . . tn = cc(f1) ≠ 0, so take
. Let ti = cc(qi). Then t = t1. . . tn = cc(f1) ≠ 0, so take  for each i. Thus hi
for each i. Thus hi  gi in
gi in  so hi is irreducible in
so hi is irreducible in  . Clearly cc(hi) = 1 for all i. Finally f = txnh1h2
. Clearly cc(hi) = 1 for all i. Finally f = txnh1h2  hr. If
hr. If 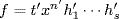 is another such factorization,
is another such factorization,  so n = n′; whence
so n = n′; whence
![]()
These are irreducible in  so r = s and (after relabeling)
so r = s and (after relabeling)  . But
. But 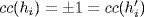 gives
gives  for all i.
for all i.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
