2.2 Groups
1.
a. Not a group. Only 0 has an inverse so G4 fails.
c. Group. It is clearly closed and
proves associativity. The unity is −1, and the inverse of a is −a − 2. Note that G is also abelian.
e. Not a group. It is not closed: (1 2)(1 3) = (1 3 2) is not in G. Note that ε is a unity and each element is self inverse, so only G1 fails.
g. Group. The unity is 16; associativity from 
. For inverses and closure —see the Cayley table:
. For inverses and closure —see the Cayley table:
i. Not a group. It is closed (by Theorem 3 §0.3), and associative, and ε is the unity. However G4 fails. If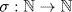 
has σn = 2n for all 
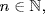then σ has no inverse because it is not onto.
has σn = 2n for all then σ has no inverse because it is not onto.
3. a.First ad = c, a2 = d by the Corollary to Theorem 6. Next ba ≠ b, a, d; and ba = c ⇒ b = ac = a(ba) = (ab)a = 1a = a, a contradiction. So ba = 1. Then bd = a, bc = d, b2 = c. Next, ca = b, cd = 1, c2 = a, cb = d. Finally, da = c, db = a, dc = 1, d2 = b.
5. A monoid is a group if each element is invertible. So check that every row and column contains exactly one 1.
7. The unity is I3 and 
shows that G is closed. Since matrix multiplication in general is associative, it remains to show that each matrix in G has an inverse in G. But
shows that G is closed. Since matrix multiplication in general is associative, it remains to show that each matrix in G has an inverse in G. But
as is easily verified.
8. a. Write σ = (1 2)(3 4), τ = (1 3)(2 4) and ϕ = (1 4)(2 3). Then σ2 = τ2 = ϕ2 = ε and στ = τσ = ϕ, σϕ = ϕσ = τ and ϕτ = τϕ = σ. Hence G is closed and every element is self inverse. Since permutation multiplication in general is associative, G is a group. Here x2 = ε for all four elements x of G.
9. It is easy to show that
and σ6 = ε. Hence G = {ε, σ, σ2, σ3, σ4, σ5} is closed by the exponent laws and σ−1 = σ5, (σ2)−1 = σ4, (σ3)−1 = σ3, (σ4)−1 = σ2 and (σ5)−1 = σ. Since permutation multiplication is associative, G is a group. Also, G is abelian because σkσl = σk+l = σlσk for all k, l. Finally, there are two elements τ satisfying τ2 = ε : τ = ε and τ = σ3; the three with τ3 = ε are τ = ε, τ = σ2 and τ = σ4.
10.
a. ab = ba2 gives aba2 = ba4 = b. Hence a2ba2 = ab, that is a2ba2 = ba2. Cancellation gives a2 = 1 . Then ab = ba2 = b, whence a = 1 by cancellation.
c. ab = ba2 gives aba4 = ba6 = b. Hence a2ba4 = ab = ba2, so a2ba2 = b by cancellation. Finally a3ba2 = ab = ba2 so a3 = 1. Hence b = aba4 = aba.
11. a. We claim that b(ab)na = (ba)n+1 for all n ≥ 0. It is clear if n = 0. If it holds for some n ≥ 0, then
Hence this holds for all n ≥ 0 by induction. Now suppose (ab)n = 1. Then (ba)n+1 = b(ab)na = b1a = ba. Cancelling ba gives (ba)n = 1.
13. α is onto because g = (g−1)−1 = α(g−1) for all g 
G. If α(g) = α(g1), then 
, so 
. This shows that α is one-to-one.
G. If α(g) = α(g1), then , so 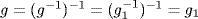. This shows that α is one-to-one.
15. Define σ : X → Xa by σ(x) = xa. This is clearly onto and σ(x) = σ(x1) implies xa = x1a, so x = x1 by cancellation. Hence σ is one-to-one.
17. If e2 = e, then ee = e1, so e = 1 by cancellation. Thus 1 is the only idempotent.
19. If G is abelian, then gh = hg, so (gh)−1 = (hg)−1 = g−1h−1 by Theorem 3. Conversely, given x, y G, we are assuming (xy)−1 = x−1y−1. By Theorem 3, this is y−1x−1 = x−1y−1; that is any two inverses commute. But this means that G is abelian because every element g of G is an inverse [in fact g = (g−1)−1].
G, we are assuming (xy)−1 = x−1y−1. By Theorem 3, this is y−1x−1 = x−1y−1; that is any two inverses commute. But this means that G is abelian because every element g of G is an inverse [in fact g = (g−1)−1].
21. If G is abelian, then (gh)2 = g(hg)h = g(gh)h = g2h2 for all g, h. Conversely, if (gh)2 = g2h2, then g(hg)h = g(gh)h. Thus hg = gh by cancellation (twice).
23. a. If g = g−1, then g2 = gg−1 = 1; if g2 = 1, then g−1 = g−11 = g−1g2 = g.
25. Let a5 = 1 and a−1ba = bm. Then
Next 
. This continues to give 
and finally 
. Hence 
by cancellation.
. This continues to give and finally . Hence by cancellation.
27. In multiplicative notation, a1 = a, a2 = a · a, a3 = a· a · a, . . .; in additive notation a + a = 2a, a+ a + a = 3a, . . .. In 
, 
, so 
is generated by 1.
, , so 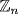is generated by 1.
29.
b.We first establish left cancellation: If gx = gy in G, then x = y. In fact, let hg = e. Then gx = gy implies x = ex = hgx = hgy = ey = y. Thus hg = e = ee = hge, so g = ge by left cancellation. This shows that e is the unity. Finally, h(gh) = (hg)h = eh = h = he, so gh = e, again by left cancellation. Thus h is the inverse of g.
2. Choose g G and let ge = g, e G (by hypothesis). If zg = e, z G, then e = zg = zge = ee = e2. Now, given h G, let h = ex. Then, eh = e2x = ex = h. Similarly, h = ye, y G, implies he = h. Thus e is the unity for G. But now, given h, we can find c, d such that ch = e = hd. Then c = ce = c(hd) = (ch)d = ed = d, so ch = e = hc. Thus h has an inverse.
G and let ge = g, e G (by hypothesis). If zg = e, z G, then e = zg = zge = ee = e2. Now, given h G, let h = ex. Then, eh = e2x = ex = h. Similarly, h = ye, y G, implies he = h. Thus e is the unity for G. But now, given h, we can find c, d such that ch = e = hd. Then c = ce = c(hd) = (ch)d = ed = d, so ch = e = hc. Thus h has an inverse.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.