3.1 Examples and Basic Properties
1.
a. Not an additive group; only 0 has an inverse.
c. It is an additive abelian group (as in Example 4), unity is  , multiplication is associative (it is function composition). But h
, multiplication is associative (it is function composition). But h  (f + g) = h
(f + g) = h  f + h
f + h  g fails: h
g fails: h  (f + g)(x) = h[f(x) + g(x)] while
(f + g)(x) = h[f(x) + g(x)] while
![]()
These may not be equal. Note that (f + g)  h = f
h = f  h + g
h + g  h does hold.
h does hold.
3.
a. Clearly  and
and  . If
. If  and
and 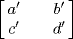 are in S then
are in S then  and
and  because
because
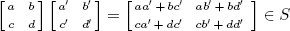 because
because
![]()

c. Clearly I, 0  S and A, B
S and A, B  S ⇒ A + B and −A
S ⇒ A + B and −A  S. To check multiplication
S. To check multiplication

5. We have 1, 0  C(X) as 1x = x = x1 and 0x = 0 = x0 for all x
C(X) as 1x = x = x1 and 0x = 0 = x0 for all x  X. If c, d
X. If c, d  C(x) then
C(x) then
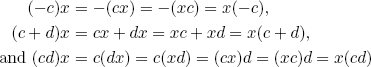
show that −c, c + d, and cd are in C(x).
6.
a. If ab = 0 and a ≠ 0 then a−1 exists so b = a−1ab = 0.
7. If 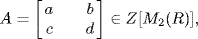 then
then 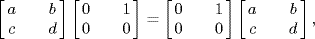 that is
that is  . Hence c = 0 and a = d, so
. Hence c = 0 and a = d, so  . Similarly the fact that A commutes with
. Similarly the fact that A commutes with  forces b = 0. Finally
forces b = 0. Finally  shows ar = ra for all r
shows ar = ra for all r  R; that is a
R; that is a  Z(R). Conversely if
Z(R). Conversely if  . Thus
. Thus
![]()
8.
a. If (a + b)(a − b) = a2 − b2. Then a2 + ba − ab − b2 = a2 − b2; whence ba − ab = 0, ab = ba. Conversely if ab = ba then
![]()
9.
![]()
![]()
Hence a + b + a + b = a + a + b + b, so b + a = a + b (additive cancellation on the left and on the right).
10.
a. ab + ba = 1 gives aba + ba2 = a, so ba2 = a − aba. Similarly a2b = a − aba so a2b = ba2. Then ab = a3b = a(a2b) = aba2 = (1 − ba)a2 = a2 − ba. Hence a2 = ab + ba = 1.
11. If a2 = 0 implies a = 0, let an = 0, n ≥ 1. If a ≠ 0, let am = 0, am−1 ≠ 0. Then m ≥ 2 and so (am−1)2 = a2m−2 = 0 since 2m − 2 ≥ m (m ≥ 2). This contradicts the hypothesis. So a = 0. The converse is clear.
13. By the hint:  . Hence
. Hence
![]()
is a unit, being a product of units [Theorem 2.5]. Thus
![]()
15. (3) ⇒ (1). Let e be the unique right unity. Given b  R,
R,
![]()
for all r  R. Hence e + eb − b is a right unity too, so e = e + eb − b by uniqueness. Thus eb = b for all b, that is e is also a left unity.
R. Hence e + eb − b is a right unity too, so e = e + eb − b by uniqueness. Thus eb = b for all b, that is e is also a left unity.
16.
a. This is by the subring test since 0 = 01R; 1R = 11R ; k1R + m1R = (k + m)1R; −(k1R) = (− k)1R and (k1R)(m1R) = (km)1R. To see that  is central, let s
is central, let s  R. Then (k1R)s = (k1R)(1s) = (k1)(1Rs) = ks by Theorem 2, and s(k1R) = ks in the same way.
R. Then (k1R)s = (k1R)(1s) = (k1)(1Rs) = ks by Theorem 2, and s(k1R) = ks in the same way.
c. If char R = 0 define  by σ(k) = k1R. Then σ(km) = σ(k) · σ(m) and σ(k + m) = σ(k) + σ(m) as in (b), and σ(k) = σ(m) ⇒ (k − m)1R = 0 ⇒ k = m because o(1R) =∞. Since σ is clearly onto, it is an isomorphism.
by σ(k) = k1R. Then σ(km) = σ(k) · σ(m) and σ(k + m) = σ(k) + σ(m) as in (b), and σ(k) = σ(m) ⇒ (k − m)1R = 0 ⇒ k = m because o(1R) =∞. Since σ is clearly onto, it is an isomorphism.
17. If R has characteristic 1 then 1 · 1R = 0, 1R = 0. Hence R = 0, the zero ring.
18.
a. 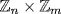 . The unity is (1, 1) so k(1, 1) = 0
. The unity is (1, 1) so k(1, 1) = 0  k1 = 0 in
k1 = 0 in 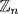 and k1 = 0 in
and k1 = 0 in  and m|k. So the characteristic of
and m|k. So the characteristic of 
c. 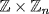 . k(1, 1) = 0
. k(1, 1) = 0  k1 = 0 in
k1 = 0 in  and k1 = 0 in
and k1 = 0 in  . So the characteristic of
. So the characteristic of  is 0.
is 0.
19. If u  R∗,
R∗,  , then k1 = 0 in R ⇒ ku = 0. But
, then k1 = 0 in R ⇒ ku = 0. But
![]()
So o(u) = o(1) = char R (since char R< ∞).
21.
a. (1 − 2e)2 = (1 − 2e)(1 − 2e) = 1 − 2e − 2e + 4e2 = 1.
22.
a. If a = (1 − e)re then ea = 0 and ae = a. Hence a2 = (ae)a = a(ea) = 0. Similarly if b = er(1 − e), then eb = b, be = 0, so b2 = 0.
c. This follows from (a) and Example 17.
23. (2) ⇒ (1). If r  R, f = e + (1 − e)re is an idempotent, so ef = fe by (2). Hence re = ere. Similarly re = ere, so re = re and e is central.
R, f = e + (1 − e)re is an idempotent, so ef = fe by (2). Hence re = ere. Similarly re = ere, so re = re and e is central.
24. (1) ⇒ (2). If an = 0 then 1 + a is a unit [(1 + a)−1 = 1 − a + a2 −  ]. Hence r(1 + a) = (1 + a)r for all r
]. Hence r(1 + a) = (1 + a)r for all r  R, that is ra = ar for all r.
R, that is ra = ar for all r.
25. If r3 = r then e = r2 is idempotent. Iterating r3 = r: r9 = r3 = r, r27 = r3 = r, and in general  for k ≥ 1. Hence if rn = 0 then
for k ≥ 1. Hence if rn = 0 then  for any k such that if 3k ≥ n. Thus R has no nonzero nilpotents. Hence idempotents in R are central by Example 18, so r2 is central for all r. Finally, if r, s
for any k such that if 3k ≥ n. Thus R has no nonzero nilpotents. Hence idempotents in R are central by Example 18, so r2 is central for all r. Finally, if r, s  R, rs = (rs)3 = (rs)2rs = r(rs)2s = r2srs2 = s2srr2 = s3r3 = sr.
R, rs = (rs)3 = (rs)2rs = r(rs)2s = r2srs2 = s2srr2 = s3r3 = sr.
26.
a. If ab = 1 and R = {r1, r2, . . ., rn} then br = bs ⇒ r = s in R. But then br1, br2, . . ., brn are all distinct, so {br1, br2, . . ., brn} = R. In particular bc = 1 for some c. Then a = a(bc) = (ab)c = c so 1 = bc = ba.
27.
a. If am = am+n then
![]()
Then am+t = am+t+kn for all t ≥ 0, so ar+kn = ar for all r ≥ m and for all k ≥ 1. We want r and k such that r + kn = 2r; that is kn = r. Since n ≥ 1 choose k such that kn ≥ m, and take r = km. Then ar is an idempotent.
28.
a.  . Units: ±1; idempotents: 0,1; nilpotents: 0.
. Units: ±1; idempotents: 0,1; nilpotents: 0.
c. 

29. It is clearly an additive abelian group and  . The associative and distributive laws hold for all matrices. Units:
. The associative and distributive laws hold for all matrices. Units:  ; nilpotents:
; nilpotents:  ; idempotents:
; idempotents:  .
.
31. If m is odd then m2 − m = (m − 1)m is a multiple of 2m. Thus  in
in 
33. If r2 = r for all r  R, then
R, then
![]()
Hence 0 = r + r = 2r. Since R ≠ 0, this shows that R has characteristic 2. In particular, −r = r for all r  R. If r, s
R. If r, s  R, then
R, then
![]()
Thus rs + sr = 0, so sr = − rs = rs. Thus R is commutative.
35. Define
![]()
It is clear that σ is a bijection and preserves addition. As to multiplication
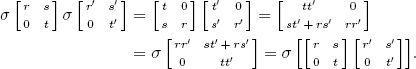
Hence σ is an isomorphism.
36.
a. If 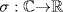 is an isomorphism let
is an isomorphism let  . Then
. Then
![]()
which is impossible for  . So no such isomorphism exists.
. So no such isomorphism exists.
c. If  is an isomorphism and
is an isomorphism and 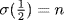 , then
, then
![]()
a contradiction in  So no such isomorphism exists.
So no such isomorphism exists.
37. Put σ(1) = e. Given r′  R′, write r′ = σ(r), r
R′, write r′ = σ(r), r  R. Then
R. Then
![]()
Similarly r′e = r′, so e is the unity of R′.
38. Let  be an isomorphism.
be an isomorphism.
a. If z  Z(R) let s
Z(R) let s  S, say s = σ(r). Then
S, say s = σ(r). Then
![]()
so σ(z)  Z(S). If z′
Z(S). If z′  Z(S) and
Z(S) and 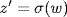 , then for any
, then for any
![]()
Since σ is one-to-one, wr = rw. Thus 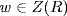 . It follows that σ : Z(R) → Z(S) is onto. It is clearly one-to-one and so is an isomorphism of rings.
. It follows that σ : Z(R) → Z(S) is onto. It is clearly one-to-one and so is an isomorphism of rings.
39. It is a routine matter to verify that α + β and αβ are again endomorphisms. The distributive law α(β + γ) = αβ + αγ follows because, for all x  X:
X:
![]()
The other distributive law is similar, as are the rest of the axioms. The zero is the zero endomorphism θ : X → X where θ(x) = 0 for all x  X, and 1X is the unity.
X, and 1X is the unity.
41. If a  (eRe)∗, let ab = e, b
(eRe)∗, let ab = e, b  (eRe)∗. Write f = 1 − e, so ef = 0 = fe and e + f = 1. Then
(eRe)∗. Write f = 1 − e, so ef = 0 = fe and e + f = 1. Then
![]()
because af = (ae)f = 0 and fb = f(eb) = 0. Thus σ : (eRe)∗ → R∗ is a mapping, and (∗) shows it is a group homomorphism. It is one-to-one because σ(a) = σ(b) means a + f = b + f, so a = b.
42.
a. Let  , pi distinct primes, ni ≥ 1. If
, pi distinct primes, ni ≥ 1. If  is nilpotent in
is nilpotent in  then km ≡ 0 (mod n) so n|km. Hence pi|km for all i so pi|k. Conversely, if pi|k for all i then p1p2
then km ≡ 0 (mod n) so n|km. Hence pi|km for all i so pi|k. Conversely, if pi|k for all i then p1p2  pr|k because the pi are relatively prime in pairs. Hence if m = max {n1, . . ., nr} then km = 0.
pr|k because the pi are relatively prime in pairs. Hence if m = max {n1, . . ., nr} then km = 0.
c. Let  in
in  . Hence n|e(1 − e). Then we can write n = ab, a|e, b|(1 − e). [Exercise 35 §1.2], say e = xa, 1 − e = yb. Thus 1 = xa + yb and e = xa.
. Hence n|e(1 − e). Then we can write n = ab, a|e, b|(1 − e). [Exercise 35 §1.2], say e = xa, 1 − e = yb. Thus 1 = xa + yb and e = xa.
43. Let |R| = 4. This is an additive group of order 4, so o(1) = 4 or o(1) = 2. If o(1) = 4 then R = {0, 1, 2, 3} is isomorphic to  via the obvious map. So assume o(1) = 2; that is the characteristic of R is 2. Hence r + r = 0 for all r in R. If a ≠ 0, 1 then 1 + a ≠ 0, 1, a. Hence R = {0, 1, a, 1 + a}. Thus
via the obvious map. So assume o(1) = 2; that is the characteristic of R is 2. Hence r + r = 0 for all r in R. If a ≠ 0, 1 then 1 + a ≠ 0, 1, a. Hence R = {0, 1, a, 1 + a}. Thus

the addition table is as shown (it is the Klein group). All but four entries in the multiplication table are prescribed as shown. The rest of the table is determined by the choice of a2.
1. a2 = 1 + a. The table is then as shown. This is clearly a field if it is associative. (See Section 4.3).

2. a2 = a. The table is as shown. This is isomorphic to 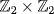 with a = (1, 0) and 1 + a = (0, 1).
with a = (1, 0) and 1 + a = (0, 1).

3. a2 = 1. The table is as shown. This is isomorphic to
![]()
with  and
and 
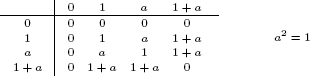
4. a2 = 0. If b = 1 + a then 1 + b = a and b2 = 1 + a2 = 1. Hence this is the same as Case 3.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
