7.1 Modules
1.
a. 0x = (0 + 0)x = 0x + 0x, so 0x = 0.
c. Using (a), x + (− 1)x = (1 + (− 1))x = 0x = 0 = x + (− x) . Now “subtract” x from both sides by adding −x to both sides.
2.
a. If α : M → N is onto and R-linear, and if M = Rx1 + 
+ Rxn, then N = Rα(x1) + + Rα(xn) . Since some of the α(xi) may be zero, the result follows.
+ Rxn, then N = Rα(x1) + + Rα(xn) . Since some of the α(xi) may be zero, the result follows.
c. Let K = Rx1 + + Rxm and let M/K = R(y1 + K) + + R(yn + K) where the xi and yj are in M. If x 
M let
+ Rxm and let M/K = R(y1 + K) + + R(yn + K) where the xi and yj are in M. If x M let
with ri R for each i. Then x − (r1y1 + + rnyn) is in K, so
R for each i. Then x − (r1y1 + + rnyn) is in K, so
where sj R for each j. Hence {x1, . . ., xm, y1, . . ., yn} generates M.
R for each j. Hence {x1, . . ., xm, y1, . . ., yn} generates M.
3. If Re is an ideal then er (Re)r ⊆ Re for any r R, say er = se, s R. Hence ere = se2 = se = er, that is er(1 − e) = 0 . As r was arbitrary, this proves eR(1 − e) = 0 . Conversely, if eR(1 − e) = 0 then er = ere for each r R. Hence er Re for all r, so Rer ⊆ Re, proving that Re is a right ideal. Hence it is an ideal.
(Re)r ⊆ Re for any r R, say er = se, s R. Hence ere = se2 = se = er, that is er(1 − e) = 0 . As r was arbitrary, this proves eR(1 − e) = 0 . Conversely, if eR(1 − e) = 0 then er = ere for each r R. Hence er Re for all r, so Rer ⊆ Re, proving that Re is a right ideal. Hence it is an ideal.
5. Recall that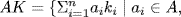 
ki K, n ≥ 1}.
ki K, n ≥ 1}.
a. Given x = Σaiki in AK and r R, then rx = Σr(aiki) = Σ(rai)ki AK because A is a left ideal.
R, then rx = Σr(aiki) = Σ(rai)ki AK because A is a left ideal.
c. If x (A + B)K then
(A + B)K then
This proves that (A + B)K ⊆ AK + BK. The reverse inclusion is similar.
7. Let K and N be submodules of M. We use the module isomorphism theorem.
a. Define α : N → (K + N)/K by α(n) = n + K for all n N. Then α is R-linear and ker α = {n 
n + K = K} = K ∩ N. So by Theorem 1 it suffices to show that α is onto. But each element of (K + N)/K has the form (k + n) + K = n + K = α(n), as required.
N. Then α is R-linear and ker α = {n n + K = K} = K ∩ N. So by Theorem 1 it suffices to show that α is onto. But each element of (K + N)/K has the form (k + n) + K = n + K = α(n), as required.
8. Let R be an integral domain. Given RM let T(M) = {x M x is torsion}.
M x is torsion}.
a. We must show T(M) is a submodule of M. Let x T(M), say ax = 0 for 0 ≠ a R. If also y T(M), say by = 0 where 0 ≠ b R, then (since R is commutative) ab(x + y) = b(ax) + a(by) = 0 + 0 = 0 . Since ab ≠ 0 (R is a domain), this shows that s + t T(M) . Similarly, if r R then
T(M), say ax = 0 for 0 ≠ a R. If also y T(M), say by = 0 where 0 ≠ b R, then (since R is commutative) ab(x + y) = b(ax) + a(by) = 0 + 0 = 0 . Since ab ≠ 0 (R is a domain), this shows that s + t T(M) . Similarly, if r R then
so rx T(M).
T(M).
9. If M = P ⊕ Q are modules, we must show that M/P ≅ Q and M/Q ≅ P. Define π : M = P ⊕ Q → Q by π(p + q) = q for all p P and q Q. This is well defined because if p + q = p1 + q1 then p − p1 = q − q1 P ∩ Q = 0, whence q − q1. It is easy to see that π is an onto R-morphism, and ker π = P. Hence the isomorphism theorem gives M/P ≅ Q. A similar argument shows M/Q ≅ P.
P and q Q. This is well defined because if p + q = p1 + q1 then p − p1 = q − q1 P ∩ Q = 0, whence q − q1. It is easy to see that π is an onto R-morphism, and ker π = P. Hence the isomorphism theorem gives M/P ≅ Q. A similar argument shows M/Q ≅ P.
11.
a. Yes. (m, n) = (n, n) + (m − n, 0) shows that M = K+ X ; clearly K ∩ X = 0.
c. Yes. (m, n) = (3m − 2n, 3m − 2n) + (2(n − m), 2(n − m)) shows that M = K + X. If (m, n) K ∩ X, then (m, n) = (k, k) and (m, n) = (2l, 3l) so k = 2l and k = 3l. Hence k = 0, proving that K ∩ X = 0.
K ∩ X, then (m, n) = (k, k) and (m, n) = (2l, 3l) so k = 2l and k = 3l. Hence k = 0, proving that K ∩ X = 0.
13. Let (k1 + + ks) + m2 + + mr = 0 in K1 ⊕ ⊕ Ks ⊕ M2 ⊕ ⊕ Mr. Then (k1 + + ks) = 0 and m2 = = mr = 0 because
+ ks) + m2 + + mr = 0 in K1 ⊕ ⊕ Ks ⊕ M2 ⊕ ⊕ Mr. Then (k1 + + ks) = 0 and m2 = = mr = 0 because
is direct. Then k1 = = ks = 0 because K1 + + Ks is direct.
= ks = 0 because K1 + + Ks is direct.
15. As in the Hint, let 1 = e + f where e A and f B. If a A then
A and f B. If a A then
because a − ae A and af B (using the fact that A and B are left ideals). Hence a = ae for all a A so, since e A, we obtain e2 = e and A ⊆ Re. But Re ⊆ A because A is a left ideal and e A, so A = Re. Now observe that f = 1 − e satisfies f2 = f, so B = Rf = R(1 − e) follows in the same way.
A and af B (using the fact that A and B are left ideals). Hence a = ae for all a A so, since e A, we obtain e2 = e and A ⊆ Re. But Re ⊆ A because A is a left ideal and e A, so A = Re. Now observe that f = 1 − e satisfies f2 = f, so B = Rf = R(1 − e) follows in the same way.
16.
a. We have M = π(M) + ker π because m = π(m) + (m − π(m)) for each m M and π[m − π(m)] = π(m) − π2(m) = 0 . If m π(M) ∩ ker π, let m = π(m1) with m1 M. Then 0 = π(m) = π2(m1) = π(m1) = m, so π(M) ∩ ker π = 0.
M and π[m − π(m)] = π(m) − π2(m) = 0 . If m π(M) ∩ ker π, let m = π(m1) with m1 M. Then 0 = π(m) = π2(m1) = π(m1) = m, so π(M) ∩ ker π = 0.
17. Suppose 
with αβ = 1M. If m M observe that
with αβ = 1M. If m M observe that
because αβ = 1M. Hence the fact that m = βα(m) + [m − βα(m)] shows that M = β(M) + ker (α) . But if x β(M) ∩ ker (α) and we write x = β(m), then 0 = α(x) = α[β(m)] = m, whence x = β(m) = β(0) = 0. Hence
β(M) ∩ ker (α) and we write x = β(m), then 0 = α(x) = α[β(m)] = m, whence x = β(m) = β(0) = 0. Hence
and we have proved that N = β(M) ⊕ ker (α).
18. We use Corollary 3 of Theorem 3 several times.
a. We have K ≅ X as both are isomorphic to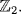 
However 
because 
while 
because 
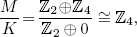However because while 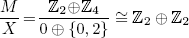because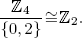
19. Since gcd (m, n) = 1 let 1 = xn + ym,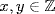 
. Then if
. Then if
Hence G = Gm + Gn. If g Gm ∩ Gn, then mg = 0 = ng so
Gm ∩ Gn, then mg = 0 = ng so
Thus G = Gm ⊕ Gn.
21. Here A is an ideal of a ring R, and RW is a module.
a. To see that 
is well defined, let 
we must show that 
We have 
say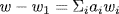 
where each ai A. Because α is R-linear, we obtain
is well defined, let we must show that We have say where each ai A. Because α is R-linear, we obtain
Hence 
as required.
as required.
23. Let α : M → N where M and N are simple. If α ≠ 0, then α(M) is a nonzero submodule of N. By hypothesis, α(M) = N, that is α is onto. Again, α ≠ 0 implies that ker (α) ≠ M. But then ker (α) = 0, again because M is simple, and we have shown that α is one to one. Hence α is an isomorphism.
24. (2) ⇒ (3). By (2), we can identify P with a summand of a finitely generated free module F, say F = P ⊕ Q, an internal direct sum. Define π : F → P by π(p + q) = p for all p P and q Q. Let {x1, xn} be a basis of F. Given the diagram we have βπ : F → N, so since α is onto, choose mi M such that α(mi) = βπ(xi) for each i. By Theorem 6, there exists an R-homomorphism θ : F → M such that θ(xi) = mi for each i. Then αθ(xi) = α(mi) = βπ(xi) for each i, so αθ = βπ because the xi span F. But then, if p P, we obtain αθ(p) = βπ(p) = β(p) because π(p) = p. Hence the restriction γ : P → M given by γ(p) = θ(p) for p P, satisfies all our requirements.
P and q Q. Let {x1, xn} be a basis of F. Given the diagram we have βπ : F → N, so since α is onto, choose mi M such that α(mi) = βπ(xi) for each i. By Theorem 6, there exists an R-homomorphism θ : F → M such that θ(xi) = mi for each i. Then αθ(xi) = α(mi) = βπ(xi) for each i, so αθ = βπ because the xi span F. But then, if p P, we obtain αθ(p) = βπ(p) = β(p) because π(p) = p. Hence the restriction γ : P → M given by γ(p) = θ(p) for p P, satisfies all our requirements.
25. As in the Hint:
i. 
is divisible. (If 
and 
then nx = q where n = 
is divisible. (If and then nx = q where n =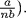
ii. If Q = K ⊕ N is divisible, then K is divisible. (If 
and k K, let nx = k, x G. If x = y + z, y K, z N, then nx = ny + nz so nx = ny because K + N is direct. Hence ny = k, y K .)
and k K, let nx = k, x G. If x = y + z, y K, z N, then nx = ny + nz so nx = ny because K + N is direct. Hence ny = k, y K .)
iii. 
is not divisible. (
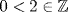and 
but 2x = 3 has no solution in 
is not divisible. ( and but 2x = 3 has no solution in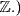
Now assume that 
is free and let {bi i I} be a basis. Then 
and 
It follows that 
is divisible, a contradiction.
is free and let {bi i I} be a basis. Then and It follows that 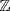is divisible, a contradiction.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.