10.1 Galois Groups and Separability
1. First ε  gal(E : F) because ε(a) = a for all a
gal(E : F) because ε(a) = a for all a  F. If σ, τ
F. If σ, τ  gal(E : F) then σ(a) = a for all a
gal(E : F) then σ(a) = a for all a  F, so a = σ−1(a) for all a; hence (since σ−1 is an automorphism) σ−1
F, so a = σ−1(a) for all a; hence (since σ−1 is an automorphism) σ−1  gal(E : F). Finally στ(a) = σ[τ(a)] = σ(a) = a, so στ
gal(E : F). Finally στ(a) = σ[τ(a)] = σ(a) = a, so στ  gal(E : F).
gal(E : F).
3. Let σ(ui) = τ(ui) for all i where σ, τ  gal(E : F). If
gal(E : F). If 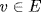 , write
, write  , ai
, ai  F. Then
F. Then
![]()
As  was arbitrary, this shows that σ = τ.
was arbitrary, this shows that σ = τ.
5. Let σ : E → E be an automorphism. Then if  , σ(n) = n · σ(1) = n. Thus
, σ(n) = n · σ(1) = n. Thus  for all
for all  131 Hence σ
131 Hence σ gal
gal 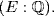
7. Put u = e2πi/6. Then u satisfies x6 − 1 = (x2 − 1)(x2 + x + 1)(x2 − x + 1), and the only roots in 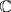 are the sixth roots of unity 1, u, u2, u3, u4, u5. But u3 = − 1 so u satisfies x3 + 1 = (x + 1)(x2 − x + 1). Hence u is a root of m = x2 − x + 1 . Since m is irreducible over
are the sixth roots of unity 1, u, u2, u3, u4, u5. But u3 = − 1 so u satisfies x3 + 1 = (x + 1)(x2 − x + 1). Hence u is a root of m = x2 − x + 1 . Since m is irreducible over 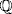 , it is the minimal polynomial of u. The other root of m is u5 (because (u5)3 = (u3)5 = (− 1)5 = − 1), so Theorem 1 gives
, it is the minimal polynomial of u. The other root of m is u5 (because (u5)3 = (u3)5 = (− 1)5 = − 1), so Theorem 1 gives  where σ(u) = u5. Note that σ2 = ε because σ2(u) = σ[σ(u)] = σ(u5) = [σ(u)]5 = u25 = u. Hence
where σ(u) = u5. Note that σ2 = ε because σ2(u) = σ[σ(u)] = σ(u5) = [σ(u)]5 = u25 = u. Hence 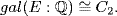
9. The minimal polynomial of i is x2 + 1, and that of  is x2 − 3. By Lemma 2, there exists a
is x2 − 3. By Lemma 2, there exists a 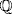 -isomorphism
-isomorphism 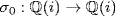 with σ0(i) = − i. This extends to an automorphism σ of
with σ0(i) = − i. This extends to an automorphism σ of  satisfying
satisfying 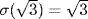 . Thus
. Thus  , σ(i) = − i and
, σ(i) = − i and  . Similarly, there exists
. Similarly, there exists  with τ(i) = i and
with τ(i) = i and  . Note that
. Note that
σ(i)  {i, − i} and
{i, − i} and  so
so  by Theorem 2. Now observe that
by Theorem 2. Now observe that
στ(i) = − i = τσ(i) and 
Hence τσ = στ by Theorem 2. Since o(σ) = 2 = o(τ), it follows that {ε, σ, τ, στ} ≅ C2 × C2. But  and
and  so
so 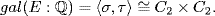
10. a. Write  . Then u satisfies x4 − 2, irreducible by the Eisenstein criterion. The roots of x4 − 2 in
. Then u satisfies x4 − 2, irreducible by the Eisenstein criterion. The roots of x4 − 2 in 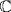 are u, −u, iu and −iu, and the only ones in
are u, −u, iu and −iu, and the only ones in  are u and −u. Thus Theorem 1 gives
are u and −u. Thus Theorem 1 gives  so
so  where σ(u) = − u.
where σ(u) = − u.
11. Choose u  E, u ∉ F. Thus [F(u) : F] ≠ 1 so, since [E : F] = 2 is prime, E = F(u) by Theorem 5 §6.2 (the multiplication theorem). If m is the minimal polynomial of u over F, then °m = 2. Thus since one root u lies in E, so does the other (their sum is the negative of the coefficient of x in m). Now the result is clear by Theorem 1.
E, u ∉ F. Thus [F(u) : F] ≠ 1 so, since [E : F] = 2 is prime, E = F(u) by Theorem 5 §6.2 (the multiplication theorem). If m is the minimal polynomial of u over F, then °m = 2. Thus since one root u lies in E, so does the other (their sum is the negative of the coefficient of x in m). Now the result is clear by Theorem 1.
13. Write  . Now x4 − 2 is irreducible (Eisenstein) so x4 − 2 and x2 + 1 are the minimal polynomials of u and i. The roots are {u, − u, iu, − iu} and {i, − i}, and all are in E so |G| ≤ 8 by Theorem 1 where
. Now x4 − 2 is irreducible (Eisenstein) so x4 − 2 and x2 + 1 are the minimal polynomials of u and i. The roots are {u, − u, iu, − iu} and {i, − i}, and all are in E so |G| ≤ 8 by Theorem 1 where  . By Lemma 1 there exists
. By Lemma 1 there exists 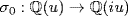 satisfying σ0(u) = iu. Extend it to an automorphism σ of
satisfying σ0(u) = iu. Extend it to an automorphism σ of  where σ(i) = i. Thus σ(u) = iu and σ(i) = i, and so σ2(u) = − u, σ3(u) = − iu, σ4(u) = u. Thus o(σ) = 4. Next let
where σ(i) = i. Thus σ(u) = iu and σ(i) = i, and so σ2(u) = − u, σ3(u) = − iu, σ4(u) = u. Thus o(σ) = 4. Next let 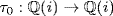 have τ0(i) = − i, extend τ0 to an automorphism τ of
have τ0(i) = − i, extend τ0 to an automorphism τ of 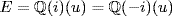 where τ(u) = u. Then τ2 = ε so o(τ) = 2. Finally
where τ(u) = u. Then τ2 = ε so o(τ) = 2. Finally
![]()
Thus στσ = τ, whence  σ, τ
σ, τ  ≅ D4. Thus |
≅ D4. Thus |  σ, τ
σ, τ  |= 8 so, since
|= 8 so, since  σ, τ
σ, τ  ⊆ G and |G| = 8, G =
⊆ G and |G| = 8, G =  σ, τ
σ, τ  ≅ D4.
≅ D4.
15. a. If  and
and 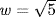 , then
, then  is 0 or
is 0 or 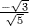 . So a = 1 is none of these, whence
. So a = 1 is none of these, whence 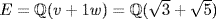 by the proof of Theorem 6.
by the proof of Theorem 6.
16. a. If  and
and 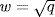 , then
, then  is 0 or
is 0 or  . So a = 1 is neither of these, whence
. So a = 1 is neither of these, whence 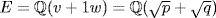 by the proof of Theorem 6.
by the proof of Theorem 6.
17. If 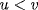 then
then  for some
for some  . If σ ≠ ε in gal(
. If σ ≠ ε in gal( then
then 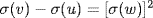 and
and  . Now let
. Now let  . If u ≠ σ(u) let u < σ(u). If u < a < σ(u),
. If u ≠ σ(u) let u < σ(u). If u < a < σ(u),  , then σ(u) < σ(a) = a, a contradiction. A similar argument diminates σ(u) < u.
, then σ(u) < σ(a) = a, a contradiction. A similar argument diminates σ(u) < u.
19. We proceed by induction on n. If n = 1 then E = F(u1) = {f(u1)  f
f  F[x]} . Hence σ(f(u1)) = f(σ(u1)) = f(τ(u1)) = τ(f(u1)) for all f, as required. In general, write K = F(u1, u2, . . ., un−1) so that E = K(un) . By induction, σ = τ on K, so σ, τ
F[x]} . Hence σ(f(u1)) = f(σ(u1)) = f(τ(u1)) = τ(f(u1)) for all f, as required. In general, write K = F(u1, u2, . . ., un−1) so that E = K(un) . By induction, σ = τ on K, so σ, τ gal(K : F) . Since σ(un) = τ(un) the result follows from the case n = 1.
gal(K : F) . Since σ(un) = τ(un) the result follows from the case n = 1.
21. Let σ  gal (F(t) : F). If
gal (F(t) : F). If  , f, g relatively prime in F[t], then
, f, g relatively prime in F[t], then  , so if
, so if  , σ(λ(t)) = λ(σ(t)). Thus σ is determined completely by f and g. Clearly f ≠ 0, g ≠ 0. Now suppose
, σ(λ(t)) = λ(σ(t)). Thus σ is determined completely by f and g. Clearly f ≠ 0, g ≠ 0. Now suppose  . Then
. Then  . Suppose
. Suppose
![]()
Then
![]()
Suppose n > m. Then
![]()
Since anfn is the only term not involving g, it follows that g|anfn. Hence g|an since f, g are relatively prime, so °g = 0. Similarly n < m implies that g|bmtfm so, again, °g ≤ 1 . Thus either °g ≤ 1 or n = m. But if n = m we have t(b0gn + b1fgn−1 +  + bnfn) = a0gn +
+ bnfn) = a0gn +  + anfn. This yields g|(an − bnt)fn and °g ≤ 1 in all cases. Now observe that
+ anfn. This yields g|(an − bnt)fn and °g ≤ 1 in all cases. Now observe that  so
so  . Hence
. Hence 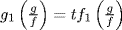 and the same type of argument implies °f ≤ 1. Hence we have proved that
and the same type of argument implies °f ≤ 1. Hence we have proved that 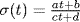 so that σ = σM where
so that σ = σM where  . Now observe that σM[σN(λ(x))] = σNMλ(x) holds for all λ(t)
. Now observe that σM[σN(λ(x))] = σNMλ(x) holds for all λ(t)  F(t). In particular if σ
F(t). In particular if σ  gal(F(t) : F) and σ = σM, and if σ−1 = σN, we have
gal(F(t) : F) and σ = σM, and if σ−1 = σN, we have 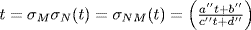 where
where  . It follows that c′′x2 + d′′x = a′′x + b′′ so c′′ = b′′ = 0, a′′ = d′′ ≠ 0 so
. It follows that c′′x2 + d′′x = a′′x + b′′ so c′′ = b′′ = 0, a′′ = d′′ ≠ 0 so  and so
and so  . Thus the map M
. Thus the map M  σM from GL2(F) → gal (F(t) : F) is an onto group homomorphism. Moreover the above shows that the kernel is Z.
σM from GL2(F) → gal (F(t) : F) is an onto group homomorphism. Moreover the above shows that the kernel is Z.
22. a. (3) ⇒ (1). Let E ⊇ F be a field and suppose f has a repeated root u in E. Then f(u) = 0 = f′(u) by Theorem 3 §6.4. But (3) implies 1 = fg + f′h in F[x] with g, h  F[x], and this is valid in E[x]. But then, taking x = u gives 1 = 0 in E, a contradiction.
F[x], and this is valid in E[x]. But then, taking x = u gives 1 = 0 in E, a contradiction.
23. Here f′ = nxn−1 − 1. Write d = gcd (f, f′); we must show d = 1 by the preceding exercise. Let E ⊇ F be a splitting field for f. If d ≠ 1 then °d > 1 so d has a root u in E. Thus f(u) = 0 = f′(u) so un = u and nun−1 = 1. Hence (n − 1)u = 0, a contradiction if char F = 0 . But if char F = p it implies p|(n − 1), contrary to hypothesis.
25. If E ⊇ F and f  F[x] is separable over F, let q be any irreducible factor of f in E[x]. We must show that q has no repeated root in E. Now f = p1p2
F[x] is separable over F, let q be any irreducible factor of f in E[x]. We must show that q has no repeated root in E. Now f = p1p2  pr in F[x] where the pi are irreducible and (by hypothesis) separable. But f = p1p2
pr in F[x] where the pi are irreducible and (by hypothesis) separable. But f = p1p2  pr in E[x] so q|pi for some i. Hence any repeated root of q in some splitting field of f would be a repeated root of pi, contrary to assumption. So q is separable.
pr in E[x] so q|pi for some i. Hence any repeated root of q in some splitting field of f would be a repeated root of pi, contrary to assumption. So q is separable.
27. Suppose f = xp − a is not a power of a linear polynomial in F[x]; we must show it is irreducible. If u is a root of f in an extension E ⊇ F, then up = a so f = xp − up = (x − u)p in E[x] because the characteristic is p. Then u ∉ F and F(u) is a splitting field of f over F. Let q be an irreducible factor of f in F[x]. Then q|(x − u)p in E[x] so q = (x − u)t. Then t > 1 because u ∉ F so q′ = 0 by Lemma 5. Hence q = g(xp) by Theorem 4. Thus, the factorization of f into irreducibles in F[x] takes the form
![]()
Since def f = p, it follows that f = gi(xp) = qi for some i, so f is irreducible.
28.
a. (3) ⇒ (1). If E ⊇ F is algebraic and u  E, the minimal polynomial of u is separable by (3), and so E ⊇ F is a separable extension.
E, the minimal polynomial of u is separable by (3), and so E ⊇ F is a separable extension.
c. Let E ⊇ F be algebraic, F perfect. If K ⊇ E is algebraic, then K ⊇ F is algebraic by Corollary 1, Theorem 6 §6.2, hence separable by hypothesis.
29.
a. If F is perfect, and a  F, let E be the splitting field of f = xp − a. If u
F, let E be the splitting field of f = xp − a. If u  E is a root of f then up = a, so f = xp − a = xp − up = (x − u)p. Let q be an irreducible factor of f in F[x]. Then q = (x − u)m. But E ⊇ F is finite, hence separable by hypothesis. Thus q has distinct roots, whence m = 1 and q = x − u. But then u
E is a root of f then up = a, so f = xp − a = xp − up = (x − u)p. Let q be an irreducible factor of f in F[x]. Then q = (x − u)m. But E ⊇ F is finite, hence separable by hypothesis. Thus q has distinct roots, whence m = 1 and q = x − u. But then u  F and up = a, as required.
F and up = a, as required.
Conversely, let q be irreducible in F[x]. If q is not separable then q′ = 0 so q = f(xp) for some f  F[x] by Theorem 4, say
F[x] by Theorem 4, say  . By hypothesis, let
. By hypothesis, let  , bi
, bi  F. Then
F. Then
![]()
This contradicts the irreducibility of q.
30.
a. Let q be the minimal polynomial of u over F. If K = F(up) let m  K[x] be the minimal polynomial of u over K. Then q
K[x] be the minimal polynomial of u over K. Then q  K[x] and q(u) = 0, so m|q. But q has distinct roots by hypothesis, so m has distinct roots. On the other hand, xp − up
K[x] and q(u) = 0, so m|q. But q has distinct roots by hypothesis, so m has distinct roots. On the other hand, xp − up  K[x] and xp − up = (x − u)p in E[x]. Hence m|(x − u)p so m = (x − u)r. Since m has distinct roots, r = 1 and so u
K[x] and xp − up = (x − u)p in E[x]. Hence m|(x − u)p so m = (x − u)r. Since m has distinct roots, r = 1 and so u  K.
K.
c. Extend 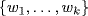 to a basis
to a basis  of E over F. Suppose
of E over F. Suppose 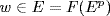 , say
, say  . Write
. Write  , so
, so  , whence
, whence 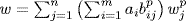 . Thus
. Thus  spans E and so is F -independent because dim E = n (Theorem 7 §6.1). But then
spans E and so is F -independent because dim E = n (Theorem 7 §6.1). But then 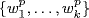 is F-independent.
is F-independent.
31. If E ⊇ F is separable, the result is Exercise 26. If E ⊇ K and K ⊇ F are separable, we may assume char F = p by the Corollary to Theorem 4. By the preceding exercise, E = K(Ep) and K = F(Kp). If u  E then
E then  where
where 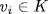 and ui
and ui  E. But
E. But  where aij
where aij  F and
F and  for all i, j. Thus
for all i, j. Thus  . Thus E ⊇ F is separable by the preceding exercise.
. Thus E ⊇ F is separable by the preceding exercise.
32.
a. Let p and q be the minimal polynomials of u over F and K respectively. Then p  K[x] and p(u) = 0, so q|p. Since p has distinct roots in some splitting field L ⊇ K, q is separable over K.
K[x] and p(u) = 0, so q|p. Since p has distinct roots in some splitting field L ⊇ K, q is separable over K.
c. Let u,  . Then F(u) ⊇ F is separable and, since
. Then F(u) ⊇ F is separable and, since  is separable over F(u) by (a),
is separable over F(u) by (a), 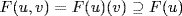 is also separable. Hence
is also separable. Hence  is separable by the preceding exercise. Since
is separable by the preceding exercise. Since 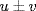 and uv are in
and uv are in  , they are separable over F, so S is a field. Clearly S ⊇ F since the minimal polynomial of a
, they are separable over F, so S is a field. Clearly S ⊇ F since the minimal polynomial of a  F is x − a, and S ⊇ F is separable by the definition of S. If E ⊇ K ⊇ F and K ⊇ F is separable, then each u
F is x − a, and S ⊇ F is separable by the definition of S. If E ⊇ K ⊇ F and K ⊇ F is separable, then each u  K is separable over F; that is u
K is separable over F; that is u  K. Hence K ⊆ S.
K. Hence K ⊆ S.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
