Appendix C: Zorn's Lemma
1. Let K ⊆ M be modules, M finitely generated, say
![]()
If  we must show that
we must show that  contains maximal members. Suppose {Xi
contains maximal members. Suppose {Xi  i ∊ I} is a chain from
i ∊ I} is a chain from 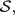 and put U = ∪ i∊IXi . It is clear that U is a submodule and that K ⊆ U, and we claim that U ≠ M . For if U = M then each xi ∊ U, and so each xi ∊ Xk for some k . Since the Xi form a chain, this means that {x1, x2, . . ., xn} ⊆ Xm for some m . Since the xi generate M this means that M ⊆ Xm, contradicting the fact that
and put U = ∪ i∊IXi . It is clear that U is a submodule and that K ⊆ U, and we claim that U ≠ M . For if U = M then each xi ∊ U, and so each xi ∊ Xk for some k . Since the Xi form a chain, this means that {x1, x2, . . ., xn} ⊆ Xm for some m . Since the xi generate M this means that M ⊆ Xm, contradicting the fact that 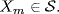 This shows that
This shows that  and so U is an upper bound for the Xi . Hence
and so U is an upper bound for the Xi . Hence 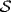 has maximal members by Zorn's lemma, as required.
has maximal members by Zorn's lemma, as required.
2. Let K ⊆ M be modules.
a. Let  is a submodule and K ∩ X = 0} . Then
is a submodule and K ∩ X = 0} . Then 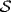 is nonempty because
is nonempty because 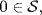 so let {Xi
so let {Xi  i ∊ I} be a chain from
i ∊ I} be a chain from  and put U = ∪ i∊IXi . It is clear that U is a submodule, and K ∩ U = 0 because K ∩ U ⊆ K ∩ Xi = 0 for each i . Hence U is an upper bound for the chain {Xi
and put U = ∪ i∊IXi . It is clear that U is a submodule, and K ∩ U = 0 because K ∩ U ⊆ K ∩ Xi = 0 for each i . Hence U is an upper bound for the chain {Xi  i ∊ I}, so
i ∊ I}, so  contains maximal members by Zorn's lemma.
contains maximal members by Zorn's lemma.
3. Let  be the set of all prime ideals of R, and partially order
be the set of all prime ideals of R, and partially order 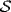 downward: Let P ≤ Q mean P ⊇ Q . We must find a maximal element in
downward: Let P ≤ Q mean P ⊇ Q . We must find a maximal element in  Let {Pi
Let {Pi  i ∊ I} be a chain from
i ∊ I} be a chain from  and put Q = ∩ i∊IPi . We claim that Q is an upper bound on {Pi
and put Q = ∩ i∊IPi . We claim that Q is an upper bound on {Pi  i ∊ I} . Clearly Q ⊆ Pi for each i, so it remains to show that Q is a prime ideal. If rs ∊ Q where r, s∊ R ; we must show that either r ∊ Q or s ∊ Q . Suppose on the contrary that r ∉ Q and s ∉ Q . Then r ∉ Pi for some i, and s ∉ Pj for some j . Since the Pi form a chain, one of Pi ⊆ Pj or Pj ⊆ Pi must hold; assume Pi ⊆ Pj . Then r ∉ Pj and s ∉ Pj but rs ∊ Pj (because rs ∊ Q ⊆ Pj) . This contradicts the fact that Pj is a prime ideal. Since we also obtain a contradiction if Pj ⊆ Pi, this proves that Q is a prime ideal.
i ∊ I} . Clearly Q ⊆ Pi for each i, so it remains to show that Q is a prime ideal. If rs ∊ Q where r, s∊ R ; we must show that either r ∊ Q or s ∊ Q . Suppose on the contrary that r ∉ Q and s ∉ Q . Then r ∉ Pi for some i, and s ∉ Pj for some j . Since the Pi form a chain, one of Pi ⊆ Pj or Pj ⊆ Pi must hold; assume Pi ⊆ Pj . Then r ∉ Pj and s ∉ Pj but rs ∊ Pj (because rs ∊ Q ⊆ Pj) . This contradicts the fact that Pj is a prime ideal. Since we also obtain a contradiction if Pj ⊆ Pi, this proves that Q is a prime ideal.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
