6.7 An Application to Cyclic and BCH Codes
1.
a. If n = 1 it is clear, if n = 2,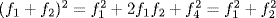 
. In general, 
. In general,
c. If f = a0+ a1x + 
then f′ = a1 + a3x2 + a5x4 + = g(x2) where g = a1+ a3x + . Conversely, f = g(x2) = b0+ b1x2 + b2x4 + clearly implies that f′ = 0 (as 2 = 0 in 
then f′ = a1 + a3x2 + a5x4 + = g(x2) where g = a1+ a3x + . Conversely, f = g(x2) = b0+ b1x2 + b2x4 + clearly implies that f′ = 0 (as 2 = 0 in
3. If n = 2k then
and, by induction, 
; that is 1 − xn = (1 + x)n. So the divisors of 1 − xn are 1, (1 + x), (1 + x)2, . . ., (1 + x)n, and these are a chain under divisibility.
; that is 1 − xn = (1 + x)n. So the divisors of 1 − xn are 1, (1 + x), (1 + x)2, . . ., (1 + x)n, and these are a chain under divisibility.
Conversely, if 1− xn = (1 + x)kpm where p is irreducible and p ≠ (1 + x), then neither 1+ t nor 
contains the other in Bn. If n = 2km, m odd, then 
a contradiction as m = 1 in 
where p is irreducible and p ≠ (1 + x), then neither 1+ t nor 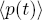contains the other in Bn. If n = 2km, m odd, then a contradiction as m = 1 in
5.
a In B4 : 1 + t, t + t2 = t(1 + t), t2 + t3 = t2(1 + t) and 1 + t3 = t3(1 + t). The other members 0, 1 + t2, t + t2 and 1 + t + t2 + t3 all lie in smaller ideals. (See Example 3.)
6.
a. We have |D| = 2 so C ∩ D = 0 or D. If n is odd then 1 + t + + tn−1 has odd parity, so C ∩ D = 0 in this case. Also, if n − 1 = 2m then
+ tn−1 has odd parity, so C ∩ D = 0 in this case. Also, if n − 1 = 2m then
is in C. Thus tn−1 
(C + D) − C. Since |C| = 2n−1 implies C is maximal, C + D = Bn. Thus Bn ≅ C × D when n is odd by Theorem 7 §3.4.
(C + D) − C. Since |C| = 2n−1 implies C is maximal, C + D = Bn. Thus Bn ≅ C × D when n is odd by Theorem 7 §3.4.
7.
a. 1 + x7 = (1 + x)(1 + x + x3)(1 + x2 + x3) so there are 2 · 2 · 2 = 8 divisors in all. Thus there are 7 codes (excluding 
).
).
c. 1 + x8 = (1 + x)8 so there are 9 − 1 = 8 codes in B8.
e. 1 + x10 = (1 + x2)(1 + x2 + x4 + x6 + x8) = (1 + x)2(1 + x + x2 + x3 + x4)2 (using Exercise 10 below). Hence there are 3 · 3 − 1 = 8 codes in B10.
9. Since ui E∗ and |E∗| = n, we have (ui)n = 1 by Lagrange's theorem. Then ui is a root of xn − 1, whence mi divides xn − 1.
E∗ and |E∗| = n, we have (ui)n = 1 by Lagrange's theorem. Then ui is a root of xn − 1, whence mi divides xn − 1.
10.
a. Since g = 1 + x + x2 + x3 + x4 has no root in 
, if it factors, it does so as
, if it factors, it does so as
Hence aa′ = 1 = cc′ so a = a′ = 1 = c = c′. Hence
so 1 + bb′ + 1 = 1 (coefficient of x2) whence b = b′ = 1. But then the coefficient of x is 1 = b + b′ = 0, a contradiction.
11. Since g = 1 + x + x4 has no root in 
, if it factorizes, it does so as
, if it factorizes, it does so as
Thus aa′ = 1 = cc′ so a = a′ = 1 = c = c′. Thus g = (1 + bx + x2)(1 + b′x + x2) so (coefficient of x3) b + b′ = 0 and (coefficient of x) b + b′ = 1. This is impossible.
13. (1 + x + x4)(1 + x3 + x4)(1 + x + x2 + x3 + x4)
= (1 + x + x3 + x4 + x5 + x7 + x8)(1 + x + x2 + x3 + x4)
= (1 + x3 + x6 + x9 + x12) .
Since (1 + x)(1 + x + x2) = 1 + x3 = 1 − x3, this verifies the factorization. We have checked that 1 + x + x4 and 1 + x + x2 + x3 + x4 are irreducible. If 1 + x3 + x4 = (a + bx + cx2)(a′ + bx′ + c′x2), then aa′ = 1 = cc′ so a = a′ = 1 = c = c′. Thus 1 + x3 + x4 = (1 + ax + x2)(1 + a′x + x2) so (coefficients of x, x3) a + a′ = 0 and a + a′ = 1, a contradiction.
15. Write m = 1 + x + + xn−1. Let 
where g divides (xn − 1). If f(t) C has odd parity, then f(t) = q(t)g(t) so 1 = f(1) = q(1)g(1). Thus g(t) has odd parity. We must show that m(t) C. Let gh = xn − 1 so
+ xn−1. Let where g divides (xn − 1). If f(t) C has odd parity, then f(t) = q(t)g(t) so 1 = f(1) = q(1)g(1). Thus g(t) has odd parity. We must show that m(t) C. Let gh = xn − 1 so
Since x + 1 is prime, either (x + 1) g or (x + 1) h. But g = λ(x + 1) gives g(1) = λ(1)(1 + 1) = 0, a contradiction. So h = k(x + 1), whence (*) gives gk(x + 1) = (x + 1)m; m = hg; m(t) g(t).
g(t).
17.
a. By Theorem 10 §4.2, let 1 = qg + ph in 
and define e = qg. Then e(t) C so e(t) ⊆ C. On the other hand 1 = e + qg so g = eg + p(1 − xn). This means g(t) = e(t)g(t) e(t), so C = e(t). Since e(t) = q(t)g(t), this gives e(t)2 = q(t)e(t)g(t) = q(t)g(t) = e(t).
and define e = qg. Then e(t) C so e(t) ⊆ C. On the other hand 1 = e + qg so g = eg + p(1 − xn). This means g(t) = e(t)g(t) e(t), so C = e(t). Since e(t) = q(t)g(t), this gives e(t)2 = q(t)e(t)g(t) = q(t)g(t) = e(t).
c. We have
We have 1 + x + x2 + x4 = x(1 + x + x3) + 1 so
So take e = x(1 + x + x3) = x + x2 + x4. Note that
So e(t) = t + t2 + t4 is the idempotent generator.
e. Given e(t) in Bn, e(t)2 = e(t2); 
. If n = 2k, and e(t)2 = e(t), this gives e(t) = e(t)n = e(tn) = e(1) = 0 or 1. In B6, e(t) = 1 + t2 + t4 is idempotent because
. If n = 2k, and e(t)2 = e(t), this gives e(t) = e(t)n = e(tn) = e(1) = 0 or 1. In B6, e(t) = 1 + t2 + t4 is idempotent because
18.
a. Given f(t) = a0 + a1t + + an−1tn−1 in Bn, write 
for the corresponding word. Then 
so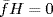 
if and only if f(ui) = 0 for all i. This is certainly true if 
the converse holds because the roots are distinct.
+ an−1tn−1 in Bn, write for the corresponding word. Then so if and only if f(ui) = 0 for all i. This is certainly true if the converse holds because the roots are distinct.
19. The roots of G are linearly independent over 
by choice, so G has rank k. Since rank R = rank G, it follows that R = [InA] by the definition of a row echelon matrix. To see that R generates C, it suffices to show that the rows of R span C. Since the rows of G span C, it suffices to show that the rows of G are all linear combinations (over 
of the rows of R. But R = UG, U invertible, so G = U−1R and the result follows.
by choice, so G has rank k. Since rank R = rank G, it follows that R = [InA] by the definition of a row echelon matrix. To see that R generates C, it suffices to show that the rows of R span C. Since the rows of G span C, it suffices to show that the rows of G are all linear combinations (over 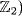of the rows of R. But R = UG, U invertible, so G = U−1R and the result follows.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.