8.3 Group Actions
1. a. If |G| = 20, there is a  G with o(a) = 5 by Cauchy's theorem. Thus |G :
G with o(a) = 5 by Cauchy's theorem. Thus |G :  a
a  |= 4 so there is a homomorphism θ : G → S4 with ker θ ⊆
|= 4 so there is a homomorphism θ : G → S4 with ker θ ⊆  a
a  . Hence |
. Hence |  a
a  /ker θ| divides 24 so ker θ ≠ {1}. Thus ker θ =
/ker θ| divides 24 so ker θ ≠ {1}. Thus ker θ = a
a  because o(a) is prime, so
because o(a) is prime, so  a
a 
 G.
G.
3. Assume p ≤ q. By Cauchy's theorem, let a  G, o(a) = q. Then H =
G, o(a) = q. Then H = a
a  has index p so H
has index p so H  G by the Corollary to Theorem 1.
G by the Corollary to Theorem 1.
5. If |H| = p then |G : H| = m so let θ : G → Sm be a homomorphism with ker θ ⊆ H. Now ker θ = {1} is impossible since |G| = pm does not divide m !. Since |H| = p, the only other possibility is ker θ = H, so H  G as asserted.
G as asserted.
6. a. If |An : H| = p let θ : An → Sp be a homomorphism with ker θ ⊆ H. Then θ is one-to-one because An is simple, so 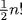 divides p !, say
divides p !, say 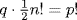 . But
. But 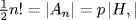 so
so  and hence p ≤ n. By hypothesis p < n. Hence
and hence p ≤ n. By hypothesis p < n. Hence 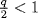 so q = 1, n ! = p !, a contradiction since n ≥ 5.
so q = 1, n ! = p !, a contradiction since n ≥ 5.
7. If U ⊆ V are subgroups then g−1Ug ⊆ g−1Vg for all g  G, so core U⊆ core V. Hence core(H∩ K) ⊆ core H ∩ score K. If x
G, so core U⊆ core V. Hence core(H∩ K) ⊆ core H ∩ score K. If x  core H∩ core K, let g
core H∩ core K, let g  G. Thus g−1(H ∩ K)g = (g−1Hg) ∩ (g−1Kg) and so x
G. Thus g−1(H ∩ K)g = (g−1Hg) ∩ (g−1Kg) and so x  g−1(H ∩ K)g. Thus x
g−1(H ∩ K)g. Thus x core (H ∩ K).
core (H ∩ K).
9. This is Exercise 26 §2.8.
10. a. H0 ⊆ H because H = 1G(H). If τ  autG then τ−1σ
autG then τ−1σ  autG for all σ
autG for all σ  autG, so H0 ⊆ τ−1σ(H). Thus τ(H0) ⊆ σ(H) for all σ, so τ(H0) ⊆ H0. Similarly τ−1(H0) ⊆ H0, whence τ(H0) = H0. Thus H0 is characteristic in G.
autG, so H0 ⊆ τ−1σ(H). Thus τ(H0) ⊆ σ(H) for all σ, so τ(H0) ⊆ H0. Similarly τ−1(H0) ⊆ H0, whence τ(H0) = H0. Thus H0 is characteristic in G.
11. (1) ⇒ (2). If X is a nontrivial finite G-set, let θ : G → SX be the homomorphism in Theorem 2. Then θ(G) ≠ {1X} because the action is not trivial, so ker θ ≠ G. Clearly  is finite.
is finite.
13. We have 0 · z = ei0z = z and b · (a · z) = eib(eiaz) = ei(a+b)z = (a + b) · z, so it is indeed an action. If z = reiθ then a · z = rei(θ+a), so the action by a is to rotate z about the origin counterclockwise through a radians. If 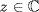 , the orbit G · z = {a · z
, the orbit G · z = {a · z  a
a  G} is the circle, center at 0, radius |z|. Given
G} is the circle, center at 0, radius |z|. Given 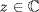 , the stabilizer is S(z) = {a
, the stabilizer is S(z) = {a  a · z = z} = {a
a · z = z} = {a  zeia = z}. Hence S(0) = G; and if z ≠ 0, then
zeia = z}. Hence S(0) = G; and if z ≠ 0, then 
15. If σ = (k1k2 )(m1m2
)(m1m2  )(n1n2
)(n1n2  )
)  , the orbits are G · k1 = {k1, k2, . . . }, G · m1 = {m1, m2, . . . }, G · n1 = {n1, n2, . . . } and so on. Clearly G · k = {k} if and only if σ fixes k.
, the orbits are G · k1 = {k1, k2, . . . }, G · m1 = {m1, m2, . . . }, G · n1 = {n1, n2, . . . } and so on. Clearly G · k = {k} if and only if σ fixes k.
17. We have x ≡ x because x = 1 · x; if x ≡ y then y = a · x for some a  G, so x = a−1 · y, y ≡ x; if x ≡ y and y ≡ z then y = a · x, z = b · y, so z = b · (a · x) = (ba) · x, that is x ≡ z.
G, so x = a−1 · y, y ≡ x; if x ≡ y and y ≡ z then y = a · x, z = b · y, so z = b · (a · x) = (ba) · x, that is x ≡ z.
19. Given G and X = {H  H is a subgroup of G}, define a · H = aHa−1. Since aHa−1 is again in X, this is an action. The fixer here is {a
H is a subgroup of G}, define a · H = aHa−1. Since aHa−1 is again in X, this is an action. The fixer here is {a  G
G  a · H = H for all H} = {a
a · H = H for all H} = {a  G
G  aHa−1 = H for all H}. This contains Z(G). If G = Q is the quaternion group, then every subgroup is normal, so F = Q. However Z(G) = {1, − 1}.
aHa−1 = H for all H}. This contains Z(G). If G = Q is the quaternion group, then every subgroup is normal, so F = Q. However Z(G) = {1, − 1}.
21. Let X = {xH  x
x  G} and let g · xH = gxH. Then H
G} and let g · xH = gxH. Then H  X and
X and
![]()
23.
a. If a, b  S(x) then (ab) · x = a · (b · x) = a · x = x and,
S(x) then (ab) · x = a · (b · x) = a · x = x and,
![]()
so ab, a−1  S(G). Since 1 · x = x, 1
S(G). Since 1 · x = x, 1  S(x) and we are done.
S(x) and we are done.
c. Assume bS(y)b−1 = S(x). Define σ : G · x → G · y by σ(g · x) = bg · y. Then
![]()
Thus σ is well defined and one-to-one; it is clearly onto. Note that if G is finite this can be proved as follows:
![]()
24. a. The fixer is F = ∩ x XS(x). If y
XS(x). If y  X then G · x = X = G · y by hypothesis, so S(x) and S(y) are conjugate subgroups by the preceding exercise, say S(y) = bS(x)b−1. Then K ⊆ S(x) gives
X then G · x = X = G · y by hypothesis, so S(x) and S(y) are conjugate subgroups by the preceding exercise, say S(y) = bS(x)b−1. Then K ⊆ S(x) gives
![]()
Thus K ⊆ ∩ y XS(y) = F.
XS(y) = F.
25. This action is well defined: If a · x = b · x then
![]()
It is clearly an action.
27. Let G act on X = {H  H ⊆ G is a subgroup} by conjugation: a · H = aHa−1. Then Xf = {H
H ⊆ G is a subgroup} by conjugation: a · H = aHa−1. Then Xf = {H  a · H = H for all a} is the set of normal subgroups of G. Hence the nonnormal subgroups are partitioned into nonsingleton conjugacy classes, and each of these has |G : N(H)| elements for some H. Since G is a p-group, this is a multiple of p, and the result follows.
a · H = H for all a} is the set of normal subgroups of G. Hence the nonnormal subgroups are partitioned into nonsingleton conjugacy classes, and each of these has |G : N(H)| elements for some H. Since G is a p-group, this is a multiple of p, and the result follows.
29. If |G : H| = p then |G : σ−1(H)| = p for all σ  autG. Hence K ⊆ σ−1(H) so σ(K) ⊆ H. It follows that σ(K) ⊆ K, so K is characteristic; in particular normal. Now if G is a p-group, Hi ≠ N(Hi) for each i by Theorem 5, so since |G : Hi| = p is prime, Hi
autG. Hence K ⊆ σ−1(H) so σ(K) ⊆ H. It follows that σ(K) ⊆ K, so K is characteristic; in particular normal. Now if G is a p-group, Hi ≠ N(Hi) for each i by Theorem 5, so since |G : Hi| = p is prime, Hi  G by Exercise 6 §8.2 and |G/Hi| = p. Let A = G/H1 ×
G by Exercise 6 §8.2 and |G/Hi| = p. Let A = G/H1 ×  × G/Hm and define θ : G → A by θ(g) = (gH1, . . ., gHm). This is a homomorphism with ker θ = K, so G/K ≅ θ(G) ⊆ A. The result follows.
× G/Hm and define θ : G → A by θ(g) = (gH1, . . ., gHm). This is a homomorphism with ker θ = K, so G/K ≅ θ(G) ⊆ A. The result follows.
31. We have 1 · (h, k) = (h, k), and
![]()
Thus it is an action. Let X = H × K so |X| = |H| |K|. Let A = H ∩ K and define λ : A → A · (h, k) by λ(a) = a · (h, k) = (ha−1, ak). This is clearly a bijection, so every orbit has |A| elements. Finally, define
![]()
by (hk)μ = A · (h, k). Then
![]()
so μ is well-defined. Conversely, a · (h, k) = (h1, k1) implies hk = h1k1, so μ is a bijection.
32.
a. (1, 1) · x = 1x1−1 = x,  = (h1h, k1k) · x = [(h1k1) · (h, k)] · x. The orbit is (H × K) · x = {(h, k) · x
= (h1h, k1k) · x = [(h1k1) · (h, k)] · x. The orbit is (H × K) · x = {(h, k) · x  h
h  H, k
H, k  K} = {hxk−1
K} = {hxk−1  h
h  H, k
H, k  K} = HxK—a double coset.
K} = HxK—a double coset.
c. The size of the double coset is
![]()
by (b). Frobenius' theorem follows.
33. a. Any two cosets aH and bH are in the same orbit because bH = (ba−1) · (aH).
34. a. This action is well-defined because [x] = [x1] gives ϕ(x) = ϕ(x1) so, since ϕ is a G-morphism,
![]()
Thus [a · x] = [a · x1] so the action is well-defined. Now 1 · [x] = [1 · x] = [x] and a · (b · [x]) = a · [b · x] = [a · (b · x)] = [(ab) · x] = (ab) · [x]. Hence 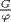 is a G-set.
is a G-set.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
