9.1 The Jordan-Hölder Theorem
1.
a. If C8 = 
g 
, o(g) = 8, then o(g2) = 4 and o(g4) = 2. It follows that C8 ⊃ g2 ⊃ g4 ⊃ {1} is a composition series. Hence length C8 = 3 and the factors are C2, C2, C2.
g , o(g) = 8, then o(g2) = 4 and o(g4) = 2. It follows that C8 ⊃ g2 ⊃ g4 ⊃ {1} is a composition series. Hence length C8 = 3 and the factors are C2, C2, C2.
c. We have D4 = {1, a, a2, a3, b, ba, ba2, ba3} where o(a) = 4, o(b) = 2, aba = b. Hence D4 ⊃ a ⊃ a2 ⊃ {1} is a composition series so length D4 = 3 and the factors are C2, C2, C2.
a ⊃ a2 ⊃ {1} is a composition series so length D4 = 3 and the factors are C2, C2, C2.
e. Q = { ± 1, ± i, ± j, ± k} and o(i) = 4. If M = i , K = − 1 , then Q ⊃ M ⊃ K ⊃ {1} is a composition series. Thus length Q = 3 and the factors are C2, C2, C2.
i , K = − 1 , then Q ⊃ M ⊃ K ⊃ {1} is a composition series. Thus length Q = 3 and the factors are C2, C2, C2.
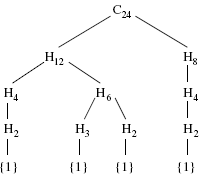
3. (a) If M is a maximal normal subgroup of C24 then C24/M is simple and abelian so |C24/M| = p is a prime. But p divides |C24| = 24 = 233, so p = 2 or p = 3. Hence |M| = 12 or 8. Let Hd denote the unique subgroup of C24 of order d where d|24. Then H12 and H8 are the maximal normal subgroups, so any composition series C24 ⊃ G1 ⊃ 
⊃ {1} must have G1 = H12 or H8. In the same way, the maximal normal subgroups of H12 are H4 and H6; of H8 is H4; of H6 are H3 and H2, and of H4 is H2. Each composition series must contain a maximal subgroup, so the various composition series are as shown. There are 4 in all.
⊃ {1} must have G1 = H12 or H8. In the same way, the maximal normal subgroups of H12 are H4 and H6; of H8 is H4; of H6 are H3 and H2, and of H4 is H2. Each composition series must contain a maximal subgroup, so the various composition series are as shown. There are 4 in all.
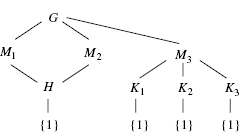
5. Write G = C4 × C2. If M is a maximal subgroup then |M| = 4 so M is cyclic or M is the Klein group. If C4 = a , o(a) = 4, and C2 = b , o(b) = 2, the elements of G of order 4 are (a, 1), (a, b), (a3, 1) and (a3, b), so the cyclic maximal subgroups are M1 = (a, 1) = (a3, 1) and M2 = (a, b) = (a3, b) . These have a unique subgroup H = (a2, 1) of order 2 leading to composition series G ⊃ M1 ⊃ H ⊃ {1} and G ⊃ M2 ⊃ H ⊃ {1}. On the other hand, the only elements of order 2 in G are (a2, 1), (a2, b) and (1, b), so M3 = {(1, 1), (a2, 1), (1, b), (a2, b)} is the unique maximal subgroup isomorphic to the Klein group. This has three subgroups of order 2: K1 = (a2, 1) , K2 = (1, b) and K3 = (a2, b) . This leads to three composition series G ⊃ M3 ⊃ K1 ⊃ {1}, G⊃M3 ⊃ K2 ⊃ {1} and G ⊃ M3 ⊃ K3 ⊃ {1}. There are thus five composition series.
a , o(a) = 4, and C2 = b , o(b) = 2, the elements of G of order 4 are (a, 1), (a, b), (a3, 1) and (a3, b), so the cyclic maximal subgroups are M1 = (a, 1) = (a3, 1) and M2 = (a, b) = (a3, b) . These have a unique subgroup H = (a2, 1) of order 2 leading to composition series G ⊃ M1 ⊃ H ⊃ {1} and G ⊃ M2 ⊃ H ⊃ {1}. On the other hand, the only elements of order 2 in G are (a2, 1), (a2, b) and (1, b), so M3 = {(1, 1), (a2, 1), (1, b), (a2, b)} is the unique maximal subgroup isomorphic to the Klein group. This has three subgroups of order 2: K1 = (a2, 1) , K2 = (1, b) and K3 = (a2, b) . This leads to three composition series G ⊃ M3 ⊃ K1 ⊃ {1}, G⊃M3 ⊃ K2 ⊃ {1} and G ⊃ M3 ⊃ K3 ⊃ {1}. There are thus five composition series.
7. Write D16 = {1, a, . . ., a15, b, ba, . . ., ba15} where o(a) = 16, o(b) = 2 and aba = b. Then Z(D16) = {1, a8} by Exercise 26 §2.6. Write Z = Z(D16). If H = a , K = a2 and L = a4 , then
a , K = a2 and L = a4 , then
is a composition series containing Z. If
then G ⊃ K ⊃ J ⊃ I ⊃ H ⊃ {1} is a composition series not containing Z.
8. a. Let n = p1p2 pm where the pi are distinct primes. Then Cn has length 1 + 1 + + 1 = m by Example 8.
pm where the pi are distinct primes. Then Cn has length 1 + 1 + + 1 = m by Example 8.
9. Define G0, G1, G2, . . . by G0 = G,
Then Gi+1 
Gi for each i and G = G0 ⊃ G1 ⊃ · · · ⊃ Gr = {1}. Since
Gi for each i and G = G0 ⊃ G1 ⊃ · · · ⊃ Gr = {1}. Since
for each i, we are done.
11. Induct on n. If n = 1 then G = G0 ⊃ G1 = {1} so G ≅ G0/G1 is finite. In general, G1 is finite by induction, and G/G1 = G0/G1 is finite by hypothesis. Thus G consists of |G/G1| cosets, each with |G1| elements. Hence G is finite. Now |G| = |G0/G1| · |G1|, and the formula follows by induction.
13. Since G has a composition series it follows that G1 G, G2 G1. . . all have composition series by Theorem 2. Hence Gi/Gi+1 has a composition series (again by Theorem 2):
G, G2 G1. . . all have composition series by Theorem 2. Hence Gi/Gi+1 has a composition series (again by Theorem 2):
Hence we obtain a subnormal series in Gi :
Moreover GikGi(k+1) ≅ Gik/Gi+1Gi(k+1)/Gi+1 is simple for all i and k, so piecing these together gives a composition series for G.
14. a. By Exercise 13, if H G and K G choose composition series for G refining
G and K G choose composition series for G refining
Now the factors in (*) between HK and K are the same as those in (**) between H and H ∩ K because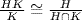 
. If H ≅ K the factors in (**) between H and H ∩ K are the same as those in (*) between K and H ∩ K (they are the factors of K ≅ H omitting those of H ∩ K). Hence the factors in (*) between HK and K are the same as those between K and H ∩ K. By hypothesis, this implies H = K.
. If H ≅ K the factors in (**) between H and H ∩ K are the same as those in (*) between K and H ∩ K (they are the factors of K ≅ H omitting those of H ∩ K). Hence the factors in (*) between HK and K are the same as those between K and H ∩ K. By hypothesis, this implies H = K.
15. a. If M ⊆ Cn is maximal normal, then Cn/M has order a prime q (being simple and abelian) and, since q divides |Cn| = n, q is one of the pi. Thus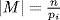 
for some i = 1, 2, . . ., r. Since Cn is cyclic, it has exactly one subgroup of order 
by Theorem 9 §2.4.
for some i = 1, 2, . . ., r. Since Cn is cyclic, it has exactly one subgroup of order 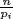by Theorem 9 §2.4.
17. See for instance: Rose, John S., A Course on Group Theory, Cambridge University Press, 1978, pp. 122–125.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.