10.3 Insolvability of Polynomials
1. a. 
contains 
, and is radical over 
because
contains 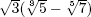, and is radical over because
has the required properties.
2. a. If f = x5 − 4x − 2 then f′ = 5x4 − 4 is zero at ±a, ±ai where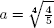 
. We find f = x(x4 − 4) − 2 so 
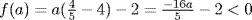while 
. As in Example 1, this shows that f has three real roots and two (conjugate) nonreal roots. Since f is irreducible by the Eisenstein criterion, its Galois group is S5 as in Example 1.
. We find f = x(x4 − 4) − 2 so while 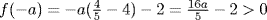. As in Example 1, this shows that f has three real roots and two (conjugate) nonreal roots. Since f is irreducible by the Eisenstein criterion, its Galois group is S5 as in Example 1.
3. Take p = x7 − 14x + 2. Then p′ = 7(x6 − 2). If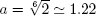 
then p′ = 0 if n = ± a, aw, aw2, aw4, aw5 where 
. Also p = x(x6 − 14) + 2 so
then p′ = 0 if n = ± a, aw, aw2, aw4, aw5 where . Also p = x(x6 − 14) + 2 so
and
Thus p has three distinct real roots and the rest complex (conjugate pairs). If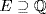 
is the splitting field, view 
as a subgroup of SX where 
is the set of roots. If we identify G with as a subgroup of SX where X is the set of p distinct roots of f, then conjugation gives a transposition in 
; if u is a real root, then 
because p is the minimal polynomial of u over 
(it is irreducible by Eisenstein). Since 
divides 
, G has an element of order 7 by Cauchy's theorem (Theorem 4 §8.2). Since the 7-cycles are the only elements in S7 of order 7, the proof in Example 1 goes through.
is the splitting field, view 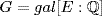as a subgroup of SX where 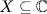is the set of roots. If we identify G with as a subgroup of SX where X is the set of p distinct roots of f, then conjugation gives a transposition in 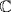; if u is a real root, then 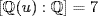because p is the minimal polynomial of u over 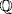(it is irreducible by Eisenstein). Since 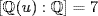divides 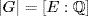, G has an element of order 7 by Cauchy's theorem (Theorem 4 §8.2). Since the 7-cycles are the only elements in S7 of order 7, the proof in Example 1 goes through.
5. Let X denote the set of roots of p in the splitting field E ⊇ F where p 
F[x]. Then G = gal(E : F) is isomorphic to a subgroup of SX. Since |X| ≤ 4, G embeds in S4. Now S4 is solvable (S4 ⊇ A4 ⊇ K ⊇ {ε} has abelian factors) so every subgroup is solvable by Theorem 3 §9.2.
F[x]. Then G = gal(E : F) is isomorphic to a subgroup of SX. Since |X| ≤ 4, G embeds in S4. Now S4 is solvable (S4 ⊇ A4 ⊇ K ⊇ {ε} has abelian factors) so every subgroup is solvable by Theorem 3 §9.2.
7. Since f′ = 3(x2 − 1), f(1) = − 1 and f(− 1) = 3, f has three real roots. Here b = − 3 and c = 1 so, in the cubic formula, p3 and q3 are roots of x2 + x + 1 which satisfy p3 + q3 = − 1 and pq = 1. The roots are 
and 
so take 
, 
. Thus
and 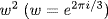so take , 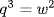. Thus
We need pq = 1 so take p = e2πi/9,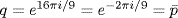 
. The roots are
. The roots are
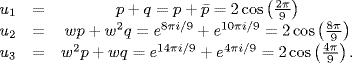
If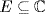 
is the splitting field, then 
and, since f is irreducible (the roots are not in 
and separable
is the splitting field, then and, since f is irreducible (the roots are not in 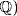and separable
Thus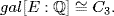 
8.
a. σ(Δ2) = Δ2 for all σ G because σ permutes the roots ui. Since E ⊇ F is Galois (f is separable because the ui are distinct) this means Δ2 G
= F.
G because σ permutes the roots ui. Since E ⊇ F is Galois (f is separable because the ui are distinct) this means Δ2 G = F.
b. The transposition γ = (uiuj) in G (regarding G ⊆ SX) changes the sign of (ui − uj) in Δ, interchanges (ui − uk) and (uj − uk), and fixes (uk − um). Hence γ(Δ) = − Δ. The even (odd) permutations are products of an even (odd) number of transpositions, so the result follows.
c. If A = {σ G 
σ is an even permutation of X} then (b) gives
G σ is an even permutation of X} then (b) gives
Write AX = {σ SX σ even} so that A = G ∩ AX. We have |SX : AX| = 2 so (Exercise 15 §2.8) either G ⊆ AX or |G : G ∩ AX| = |G : A| = 2. If G ⊆ AX then A = G = F(Δ)′. If |G : A| = 2 then (*) gives F(Δ)′ = G or F(Δ)′ = A. But F(Δ)′ = G implies σ(Δ) = Δ for all σ G so G ⊆ AX a contradiction. Thus F(A)′ = A in any case.
SX σ even} so that A = G ∩ AX. We have |SX : AX| = 2 so (Exercise 15 §2.8) either G ⊆ AX or |G : G ∩ AX| = |G : A| = 2. If G ⊆ AX then A = G = F(Δ)′. If |G : A| = 2 then (*) gives F(Δ)′ = G or F(Δ)′ = A. But F(Δ)′ = G implies σ(Δ) = Δ for all σ G so G ⊆ AX a contradiction. Thus F(A)′ = A in any case.
d. Using (c): Δ F 
F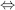(Δ) = F A = F(Δ)′ = G G ⊆ AX.
F F(Δ) = F 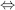A = F(Δ)′ = G 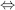G ⊆ AX.
e. If f = x2 + bx + c = (x − u1)(x − u2) then u1 + u2 = − b, u1u2 = c, so Δ2 = (u1 − u2)2 = (u1 + u2)2 − 4u1u2 = b2 − 4c.
f. If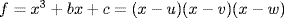 
then
then
(1) 
(2) 
(3) 
Now (1) and (2) give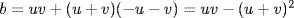 
; so 
. Thus 
. Permuting u, 
, 
:
; so 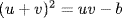. Thus 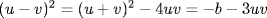. Permuting u, , :
Hence:
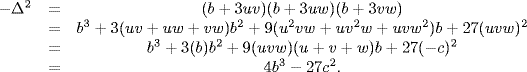
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.