1.2 Divisors and Prime Factorization
1.
a. 391=23·17+0
c. −116=(−9)·13+1
2.
a. n/d=51837/386=134.293, so q=134. Thus r=n−qd=113.
3. If d>0, then  d
d =d and this is the division algorithm. If d<0, then
=d and this is the division algorithm. If d<0, then  d
d =−d>0 so n=q(−d)+r=(−q)d+r, 0≤r≤
=−d>0 so n=q(−d)+r=(−q)d+r, 0≤r≤ d
d .
.
5. Write m=2k+1, n=2j+1. Then m2−n2=4[k(k+1)−j(j+1)]. But each of k(k+1) and j(j+1) is even, so 8  (m2−n2).
(m2−n2).
7.
a. 10(11k+4)−11(10k+3)=7, so d  7. Thus d=1 or d=7.
7. Thus d=1 or d=7.
9.
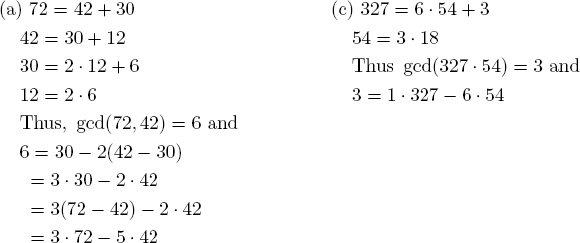

11. If m=qd, then 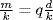 , so
, so 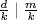 . Similarly,
. Similarly, 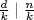 . If d=xm+yn, then
. If d=xm+yn, then 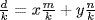 , so any common divisor of
, so any common divisor of 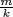 and
and 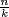 is a divisor of
is a divisor of 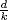 .
.
13. It is prime for n=1, 2, . . ., 9; but 102+10+11=121=112.
15. If d=gcd(m, n) and d1=gcd(m1, n1), then d  m and d
m and d  n, so d
n, so d  m1 and d
m1 and d  n1 by hypothesis. Thus d
n1 by hypothesis. Thus d  d1.
d1.
17. If 1=xm+yn and 1=x1k+y1n, then
![]()
Thus gcd(mk, n)=1 by Theorem 4. Alternatively, if d=gcd(mk, n)≠1 let p  d, p a prime. Then p
d, p a prime. Then p  n and p
n and p  mk But then p
mk But then p  m or p
m or p  k, a contradiction either way because we have gcd(m, n)=1=gcd(m, n).
k, a contradiction either way because we have gcd(m, n)=1=gcd(m, n).
19. Write d=gcd(m, n) and d′=gcd(km, kn). We must show kd=d′. First, d  m and d
m and d  n, so kd
n, so kd  km and kd
km and kd  kn. Hence, kd
kn. Hence, kd  d′. On the other hand, write km=qd′ and kn=pd′. We have d=xm+yn,
d′. On the other hand, write km=qd′ and kn=pd′. We have d=xm+yn, 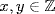 , so
, so
![]()
Thus d′  kd. As k≥1 it follows that d′=kd.
kd. As k≥1 it follows that d′=kd.
21. If p is not a prime, then assume p=mn with m≥2 and n≥2. But then p  m or p
m or p  n by hypothesis, so p≤m<p or p≤n<p, a clear contradiction.
n by hypothesis, so p≤m<p or p≤n<p, a clear contradiction.
23. No. If a=18 and n=12 then d=6 so 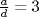 is not relatively prime to n=12.
is not relatively prime to n=12.
25. Let them be 2k+1, 2k+3, 2k+5. We have k=3q+r, r=0, 1, 2. If r=0 then 3  (2k+3); if r=1, then 3
(2k+3); if r=1, then 3  (2k+1); and if r=2, then 3
(2k+1); and if r=2, then 3  (2k+5). Thus one of these primes is a multiple of 3, and so is 3.
(2k+5). Thus one of these primes is a multiple of 3, and so is 3.
27. Let d=gcd(m, pk), then d  m and d
m and d  pk. Thus d=pj, j≤k. If j>0, then p
pk. Thus d=pj, j≤k. If j>0, then p  d, so (since d
d, so (since d  m) p
m) p  m. This contradicts gcd(m, p)=1. So j=0 and d=1.
m. This contradicts gcd(m, p)=1. So j=0 and d=1.
29. We have a  a1b1 and (a, b1)=1. Hence a
a1b1 and (a, b1)=1. Hence a  a1 by Theorem 5. Similarly a1
a1 by Theorem 5. Similarly a1  a, so a=a1 because both are positive. Similarly b=b1.
a, so a=a1 because both are positive. Similarly b=b1.
30.
a. 27783 = 34 · 73
c. 2431 = 11 · 13 · 17
e. 241 = 241 (a prime)
31.
a. 735=20·31·51·72·110 and 110=21·30·51·70·111. Hence gcd(735, 110)=20·30·51·72·110=5, and
![]()
c. 139=20·1391 and 278=21·1391. Hence gcd(139, 278)=20·1391=139, and lcm(139, 278)=21·1391=278.
33. Use Theorem 8. In forming 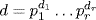 , there are (n1+1) choices for d1 among 0, 1, 2, . . ., ni; then there are (n2+1) choices for d2 among 0, 1, 2, . . ., n2; and so on. Thus there are (n1+1)(n2+1)
, there are (n1+1) choices for d1 among 0, 1, 2, . . ., ni; then there are (n2+1) choices for d2 among 0, 1, 2, . . ., n2; and so on. Thus there are (n1+1)(n2+1) (nr+1) choices in all, and each leads to a different divisor by the uniqueness in the prime factorization theorem.
(nr+1) choices in all, and each leads to a different divisor by the uniqueness in the prime factorization theorem.
35. Let 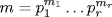 and
and 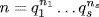 be the prime factorizations of m and n. Since gcd(m, n)=1, pi≠qj for all i and j, so the prime factorization of mn is
be the prime factorizations of m and n. Since gcd(m, n)=1, pi≠qj for all i and j, so the prime factorization of mn is 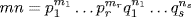 . Since d
. Since d  mn, we have
mn, we have 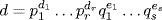 where 0≤di≤mi for each i and 0≤ej≤nj for each j. Take
where 0≤di≤mi for each i and 0≤ej≤nj for each j. Take 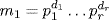 and
and 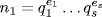 .
.
37. Write 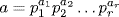 and
and 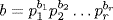 where the pi are distinct primes, ai≥0 and bi≥0. Let
where the pi are distinct primes, ai≥0 and bi≥0. Let 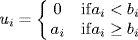 and
and 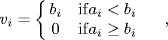 and then take
and then take 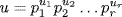 and
and 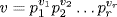 . Then u
. Then u  a,
a, 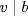 and
and 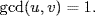 Moreover uv=lcm(a, b) by Theorem 9 because
Moreover uv=lcm(a, b) by Theorem 9 because 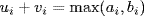 for each i.
for each i.
39.
a. By the division algorithm, p=4k+r for r=0, 1, 2 or 3. But r=0 or 2 is impossible since p is odd (being a prime greater than 2).
41.
a. 28665=32·51·72·110·131 and 22869=33·50·71·112·130 so,
![]()
43. Let 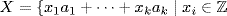 , x1a1+
, x1a1+ +xkak≥1}. Then X≠∅ because
+xkak≥1}. Then X≠∅ because 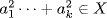 , so let m be the smallest member of X. Then m=x1a1+
, so let m be the smallest member of X. Then m=x1a1+  +xkak for integers ak, so we show d=m. Since d
+xkak for integers ak, so we show d=m. Since d  ai for each i, it is clear that d
ai for each i, it is clear that d  m. We can show m
m. We can show m  d, if we can show that m is a common divisor of the ai (by definition of d=gcd(a1,
d, if we can show that m is a common divisor of the ai (by definition of d=gcd(a1,  , ak)). Write a1=qm + r, 0≤r<m. Then
, ak)). Write a1=qm + r, 0≤r<m. Then
![]()
and this contradicts the minimality if r≥1. So r=0 and m  a1. A similar argument shows m
a1. A similar argument shows m  ai for each i.
ai for each i.
45. Let m=qn+r, 0≤r<n. If m<n, then q=0 and r=m. If m≥n, then q≥1. Thus q≥0. We want 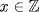 such that 2m−1=x(2n−1)+(2r−1). Solving for x (possibly in
such that 2m−1=x(2n−1)+(2r−1). Solving for x (possibly in 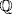 ):
):
![]()
If q=0, take x=2r=2m; if q>0, take x=(2n)q−1+ +2n+1.
+2n+1.
..................Content has been hidden....................
You can't read the all page of ebook, please click here login for view all page.
